井喷喷射火热辐射影响范围与模型对比分析研究*

周 波，梁 爽，王鹏程，罗方伟，张绪亮，郑钰山

(1.中国石油天然气股份有限公司 塔里木油田分公司，新疆 库尔勒 841000；2.中国石油集团安全环保技术研究院有限公司，北京 102206)

0 引言

天然气的需求量越来越大，我国油气井产量也逐渐增高。井喷作为1类较为常见的油气井事故，如果没有及时得到有效控制，极易造成严重的事故后果。2003年12月23日，位于重庆市开县的高含硫气井发生井喷，造成243人死亡[1-2]。

井喷时可能存在的危险源主要包括在高压下喷出的易燃易爆的石油天然气与伴随的H2S、CO等有毒气体[3]。为有效减少井喷造成的危害，一般会主动点火，避免有毒气体的扩散[4]。但是，从井内喷出的天然气一旦被点燃，会形成1个竖长的火焰，此火焰会对周围产生较高的热辐射，对井喷现场人员和设备造成间接热辐射破坏和燃烧的直接伤害[5]。因此，研究井喷喷射火周边的热辐射强度，确定点火后的应急响应距离，具有重要意义。

目前，分析热辐射强度的方法主要通过计算流体力学(CFD)软件模拟仿真，采用理论模型或经验公式等进行计算。

Flacs是工业上常用的CFD工具，常用于蒸气云扩散分析和爆炸模拟，是通过在三维笛卡尔网格上对质量、动量、能量等守恒方程进行求解来逐步模拟计算[6]。

喷射火理论模型主要有2种：点源模型和固体火源模型[7]。其中点源模型包括单点源模型和多点源模型，固体火焰模型主要指圆锥体模型。单点源模型是把喷射火看成1个点源，向周围释放能量；在此基础上，将多个点源在1条直线上进行累积，形成了多点源模型，其将喷射火看成1条线段，由此线段逐渐向四周释放能量；圆锥体模型则是将喷射火看成1个处于倒立状态的圆锥体，相比之下此种模型的能量传递方式与实际喷射火焰更为相像[8]，而Thornton模型在圆锥体模型中的应用较多。

因此，作者结合Flacs软件、Thornton模型和点源模型开展井喷喷射火热辐射强度研究，通过对比三者数值模拟计算结果来为Thornton模型添加合适的修正系数，从而使其能有效应用于井喷应急救援预警。

1 模型介绍

1.1 Flacs软件

Flacs中描述辐射场的控制方程如公式(1)所示[9]：

(1)

式中：μ是极角θ的余弦；φ是方位角，°；I(τ,μ,φ)是在垂直于表面的介质内部测得的光学深度τ上沿μ，φ方向的强度，W/m2；IB是光谱在温度T下的黑体强度，W/m2；ω是单个散射反照率，而Φ(μ′,φ′;μ,φ)是散射相位函数。

1.2 Thornton模型

Thornton模型计算热辐射见式(2)～(5)[10]:

(2)

(3)

τa=2.02×(pw×x)-0.09

(4)

q″(x)=SEPact×Fview×τa

(5)

式中：SEPmax为表面发射功率，J/(m2·s)；FS为视角系数；Fmax为最大视角系数；FV为垂直方向视角系数；Fh为水平方向视角系数；τa为空气透射率；pw为水的蒸气压，N/m2；x为喷射火表面到目标点的距离，m；q″(x)为热辐射强度，J/(m2·s)；A为火焰表面积，m2；Q′为每秒燃烧热量，J/s；A的计算表达式见文献[11]。

1.3 点源模型

点源模型计算热辐射如式(6)所示[12]：

(6)

式中：I为热辐射强度，kW/m2；η为燃烧效率，取0.35；Xg为热辐射份数，取0.2；HC为燃料热值，kJ/kg；r为井口到热辐射目标点的距离，m；Qeff为泄漏速率，kg/s。

2 计算结果分析

2.1 Flacs模拟结果

选取1 000 m×1 000 m×500 m的空间进行网格划分，核心区域网格为1 m，扩展区域扩展因子为1.2，网格总数为634 800。建模时假设井场周围环境为戈壁，无障碍物遮挡[13]。

结合塔里木油田博孜3-1井井身结构及实际工况中地层温度、压力等关键参数，运用OLGA高级井模块对塔里木博孜3-1X井井身结构及井内流体流动状况进行模拟，预测井喷速率约为140 kg/s，考虑到井喷泄漏速率的波动，取90～200 kg/s的泄漏范围，并分析不同风速对喷射火的影响。各工况条件设置如表1所示。图1是不同泄漏速率以及不同风速条件下，喷射火热辐射强度与井口距离的变化关系。

表1 Flacs模拟参数设置Table 1 Parameters setting of Flacs simulation

从图1中可以看出，热辐射强度随距离的变化呈类似反比例函数的趋势。在距井口距离逐渐增加时，热辐射强度逐渐减小，斜率的绝对值逐渐减小。

图1 Flasc软件模拟的不同工况条件下热辐射强度随距离的变化Fig.1 Variation of thermal radiation intensity with distance under different conditions simulated by Flacs

用Flacs软件的后处理模块分析不同工况下热辐射强度的二维图像，得出结果如图2所示。

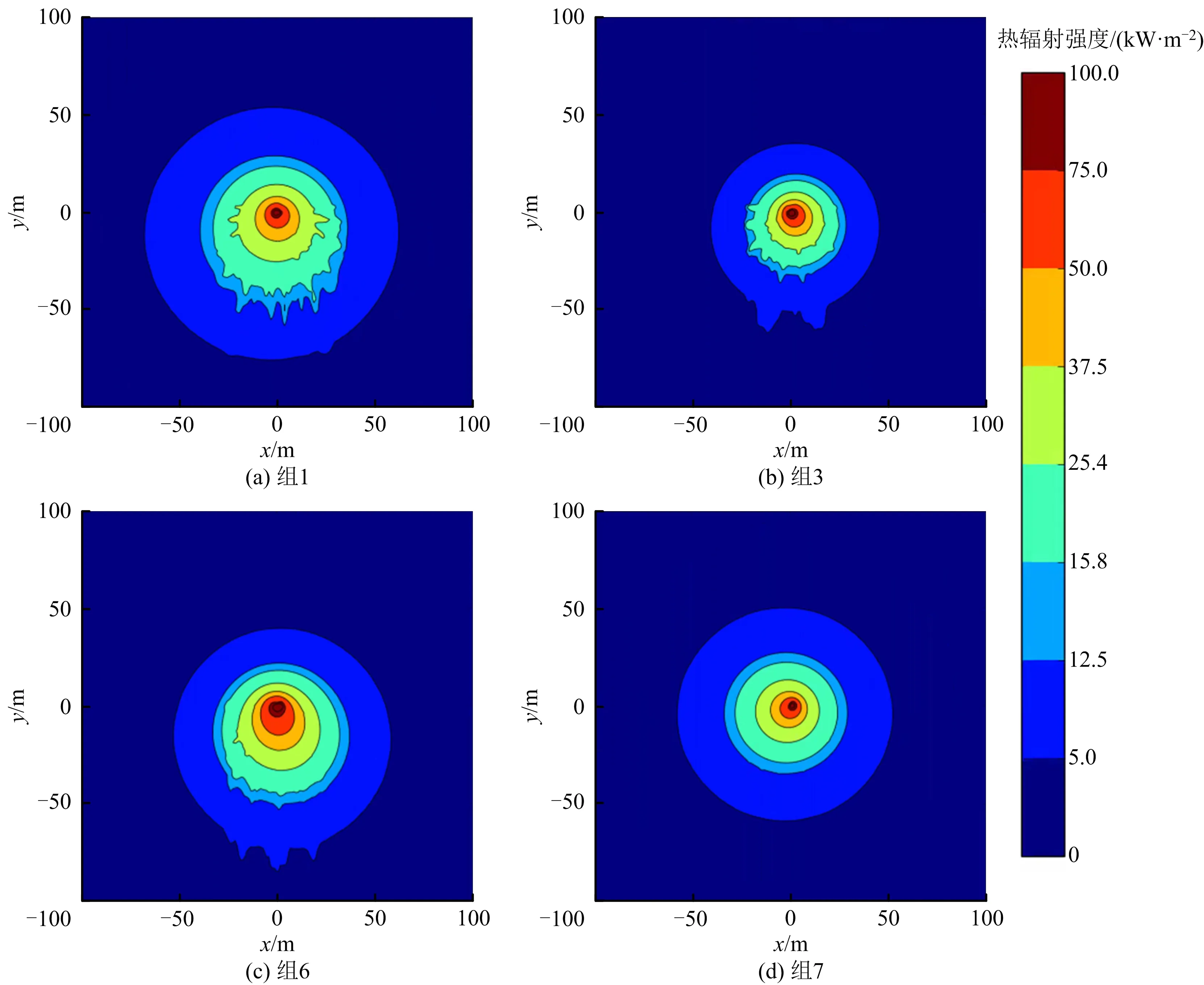
图2 地面0.5 m处热辐射强度分布Fig.2 Distribution of thermal radiation intensity at 0.5 m height from ground

根据热辐射对人体的伤害准则[14]，选择5，15.8，25.4，37.5 kW/m2作为临界热辐射剂量标准。

由图2可以看出，当泄漏速率为200 kg/s、风速为7 m/s时，附近大多区域的地表热辐射强度处于5～15.8 kW/m2之间，而当泄漏速率由200 kg/s降低至140 kg/s时，地表热辐射强度处于5～15.8 kW/m2之间的区域明显缩小，并且在上风向处更为明显。而当风速从12 m/s降低至3 m/s时，危险区域向Y-方向偏移的趋势降低了许多，更趋向于圆形。

二维图像结果与图1中结果存在差异，是因为在地面表面处的视角系数与设置在半空中的监测点的视角系数存在差异，Flacs中监测点在未指定方向时会选取最大值记录。

2.2 Thornton模型计算结果

采用固体火焰模型Thornton模型进行计算，结果如图3所示。

图3 固体火焰模型计算的不同工况条件下热辐射强度随距离的变化Fig.3 Variation of thermal radiation intensity with distance under different conditions calculated by solid flame model

由图3(a)可以看出，在Thornton模型中，泄漏速率的变化对近场的热辐射强度影响较小，200 kg/s与90 kg/s相比，在60 m处的热辐射强度差距只有16%；而在150 m处差距则达到47%，不同泄漏速率时热辐射强度随距离的变化趋势相似。

从图3(b)中可以得到，在泄漏速率为140 kg/s时，12 m/s风速与3 m/s风速的热辐射强度在60 m处相差可高达86%，在150 m处相差仍有67%，Thornton模型中，风速对近场处热辐射强度的影响很大，对远场处值的影响相对较小。

2.3 点源模型结果

点源模型忽略了风速的影响，因此采用点源模型进行计算，其结果仅与泄漏速率有关，如图4所示。

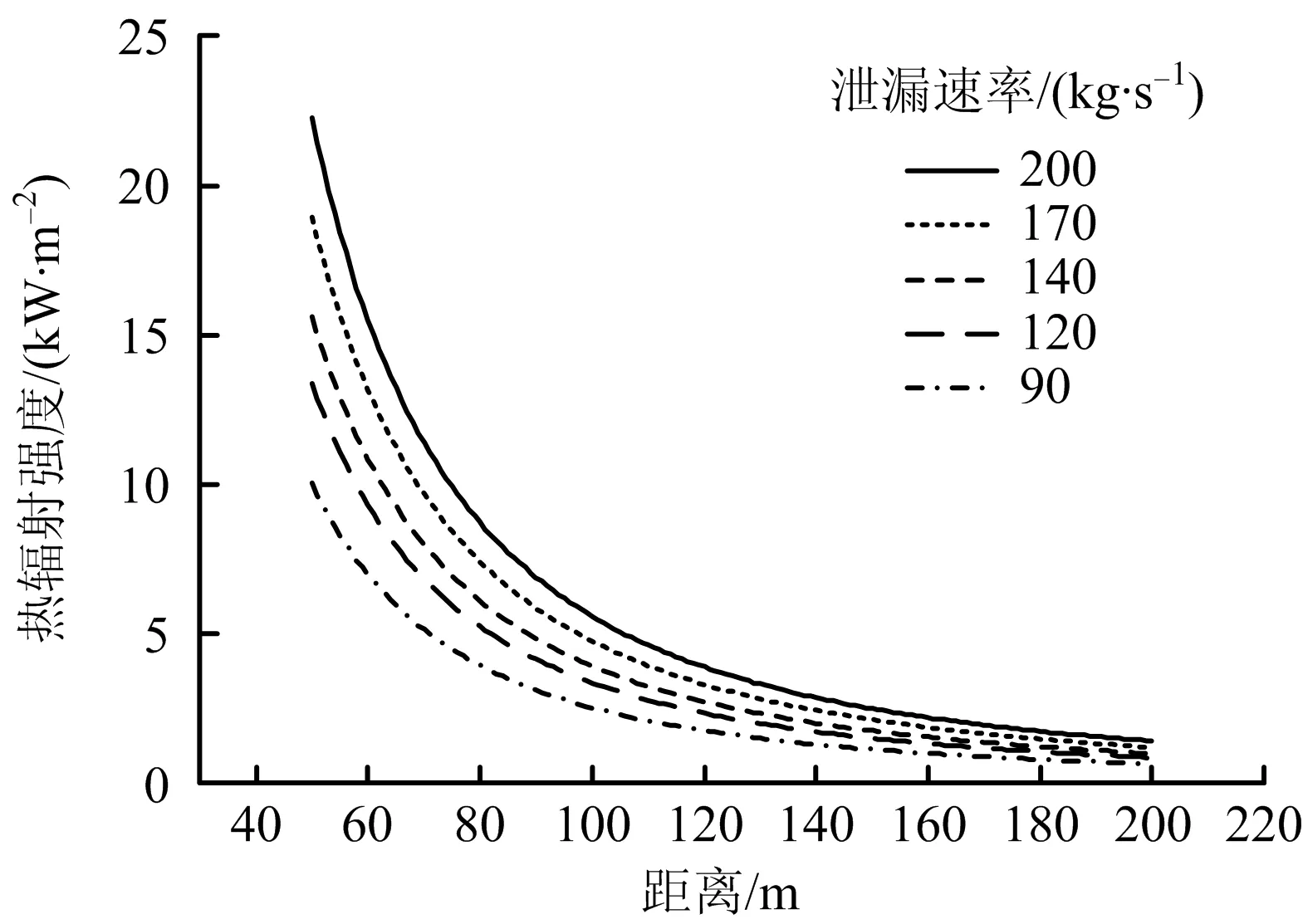
图4 点源模型计算的热辐射强度随距离的变化Fig.4 Variation of thermal radiation intensity with distance calculated by point source model

根据点源模型的计算公式，热辐射强度与泄漏速率成正比，相同泄漏速率条件下，热辐射强度与距离的平方成反比。

3 计算结果对比

3.1 热辐射强度随距离变化曲线对比

考虑到塔里木油田博孜3-1井所处戈壁环境，在模型中选取7 m/s的风速进行对比，点源模型中不再考虑风速的影响。不同泄漏速率条件下，各模型的对比结果如图5所示。

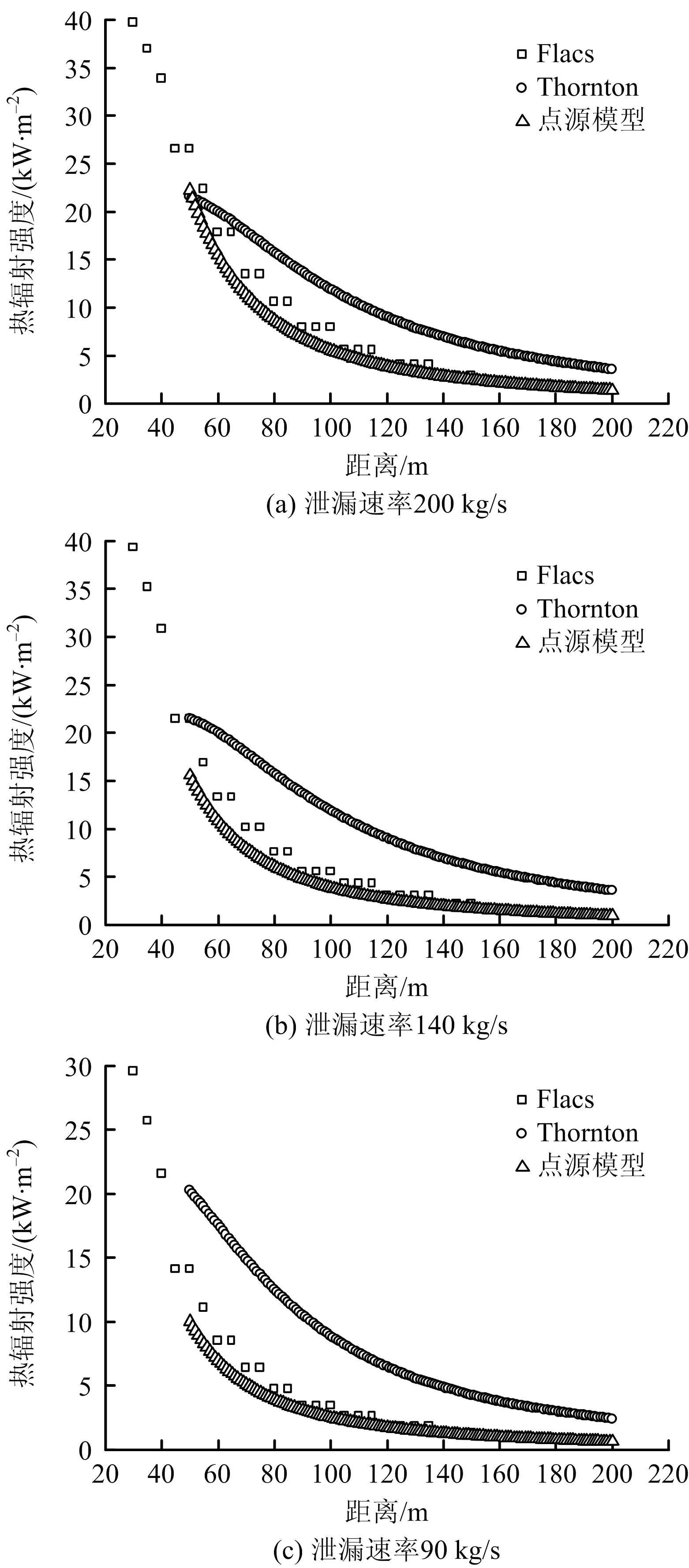
图5 3种方法计算的热辐射强度对比Fig.5 Comparison of thermal radiation intensities calculated by three methods

从图5中可以得到，在距火焰中心50m处附近，随着气体释放速率逐渐减小，Thornton模型的计算结果与Flacs和点源模型的差值逐渐增大，这是由于Thornton模型对泄漏速率变化的敏感性相较于其余模型要小；而随着距离逐渐增大，Flacs计算值与点源模型的计算值逐渐接近，说明在计算远距离热辐射强度时点源模型能够给出较好的结果。

3.2 热辐射影响范围对比

以5 kW/m2和12.5 kW/m2作为临界值，各模型分析得到井喷喷射火热辐射影响范围如图6所示。

图6 3种方法计算得到的热辐射影响范围Fig.6 Influence ranges of thermal radiation calculated by three methods

相比较而言，当泄漏速率200 kg/s时，5 kW/m2的影响范围，Flacs模拟结果比Thornton模型计算结果小47%，而与点源模型的差距仅为2%；对于12.5 kW/m2的影响范围，则分别为31%和16%。

当泄漏速率为120 kg/s时，Flacs模拟结果与Thornton模型和点源模型相比，5 kW/m2和12.5 kW/m2的影响范围，分别相差44%和7%，以及37%和10%。

因此，判断喷射火影响范围，点源模型与Flacs结果相似，而Thornton模型计算结果则明显偏大。

3.3 固定位置处的热辐射强度对比

图7和图8分别给出了不同泄漏速率条件下，在距离井口100 m和150 m位置处，3种方法分析得到的热辐射强度的对比。

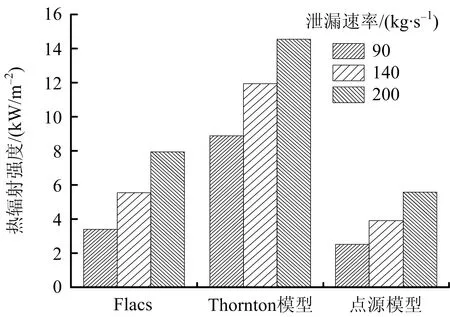
图7 3种方法计算得到距井口100 m处热辐射强度Fig.7 Thermal radiation intensities at 100 m away from wellhead calculated by three methods

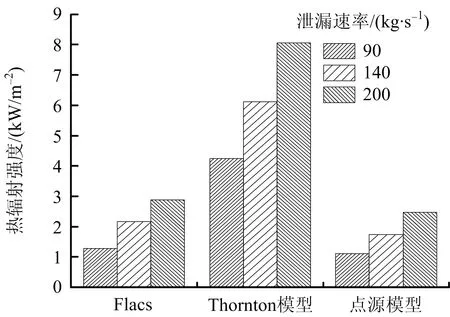
图8 3种方法计算得到距井口150 m处热辐射强度Fig.8 Thermal radiation intensities at 150 m away from wellhead calculated by three methods

对于90 kg/s的泄漏速率，Flacs模拟值是Thornton模型计算值的54.8%，点源模型计算值是Flacs模拟值的70.1%；对于140 kg/s的泄漏速率，该数值分别为46.6%和70.3%；而对于200 kg/s的泄漏速率，对比结果则分别为38.4%和73.5%。

相比之下，在距离150 m位置处，Flacs模拟结果平均为Thornton模型的33.8%，点源模型计算值则平均为Flacs模拟值的84.3%。

从上述对比结果可以看出，点源模型计算结果与Flacs模拟结果较为接近，而Thornton模型远大于2者。相比Thornton模型而言，在计算大尺度喷射火时，点源模型考虑了燃烧效率系数以修正实际燃烧时的热辐射强度。因此，结合修正系数的相关文献[11-12]，对Thornton模型的中的式(5)添加修正系数0.4，如式(7)所示：

q″(x)=SEPact×Fview×τa×η

(7)

式中：η为修正系数，η=0.4。

将修正后的Thornton模型计算结果与Flacs模拟结果进行对比，分析不同泄漏速率条件下的热辐射影响范围(以5 kW/m2作为临界值)，如图9所示。可见，在添加修正系数后，Thornton模型计算结果与Flacs模拟结果非常相近，因此可认为修正后的Thornton模型能够有效指导井喷喷射火事故发生时的紧急对策制定行动。

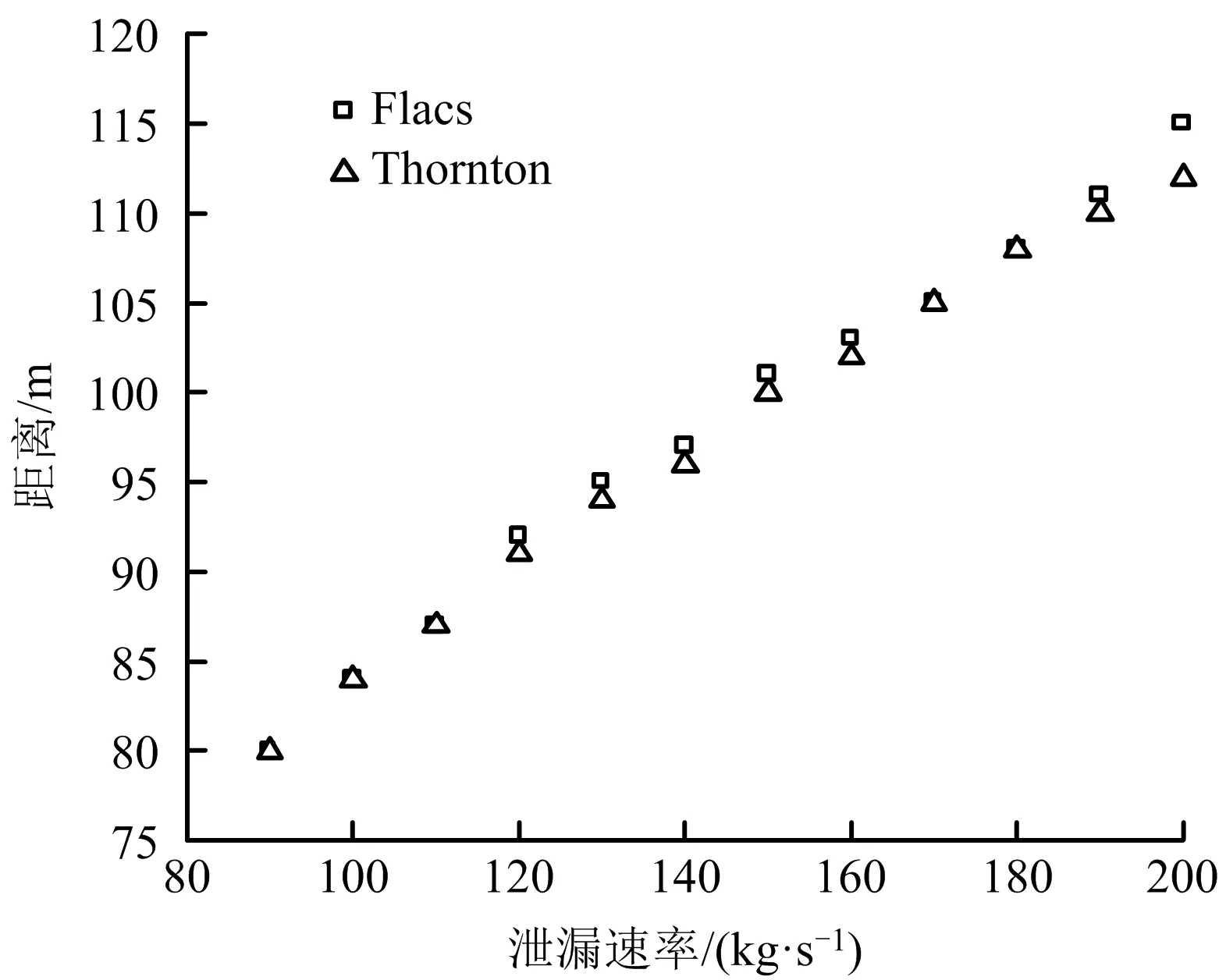
图9 修正后的Thornton模型与Flacs模拟所得热辐射影响范围对比Fig.9 Comparison on influence ranges of thermal radiation obtained by revised Thornton model and Flacs simulation

4 结论

1)利用Flacs，Thornton模型和点源经验模型分别计算不同工况下井喷喷射火的热辐射强度，并输出各模型热辐射强度随距离的变化过程，得到喷射火热辐射危险区域。

2)将不同工况下输出的曲线分别对比分析，计算相同工况下不同模型的差异程度，Thornton模型热辐射计算值最大，点源模型的计算结果最小。

3)Thornton模型的理论计算值与实际值仍有差异，但可通过添加修正系数解决此问题。而在实际应用中，尽管Flacs的模拟结果在3种模型中与真实值最为贴近，但考虑到其建模、模拟计算与后处理过程中消耗的时间，在事故发生时无法及时有效地分析事故后果严重程度。点源经验模型则有着很大的局限性，无法分析复杂工况事故。而Thornton模型在处理时间上远优于Flacs，也拥有考虑复杂工况时计算热辐射强度的能力，在添加了修正系数后即可将其用于事故发生时的临场分析。