直升机振动环境下的螺栓疲劳寿命估算方法研究

刘万川,杨 臻,王国强,苑海威,高骁波

(1.中北大学机电工程学院，山西 太原 030051)(2.中国兵器装备集团兵器装备研究所，北京 102202)

机载平台运行过程中，武器设备与机载平台的连接口会受到较大的振动与冲击，有可能发生接口破坏。机械接口断裂形式多为疲劳断裂，因此在设计接口时需要对其进行疲劳寿命估算。国内外对直升机振动的随机振动特性做了许多分析研究。张曾锠等[1]给出了直升机机载设备振动耐久性试验条件；孙东红等[2]认为直升机振动主要来自于旋翼与尾桨系统，属于低频周期振动，这些周期振动传递到机身各个部位后，形成了以周期振动为主、叠加随机振动的混合振动；季馨等[3]推导出转换公式，给出了将直升机的混合振动简化为随机振动的方法；王和伟等[4]依据直升机振动的特点，对仿真分析边界条件的设置方式和具体操作步骤进行了论述。

目前国内外学者的研究结果为估计随机振动疲劳提供了各种方法。Matsuichi等[5]提出了雨流计数法，结合材料的S-N曲线以及Miner法则即可估计结构的随机振动疲劳，为后来的学者在随机振动疲劳领域的研究提供了重要参照；焦晋峰[6]分别采用累计损伤理论、断裂力学方法与热点应力法对高强度螺栓进行了随机振动疲劳分析；叶菲[7]对时域法与频域法等随机振动疲劳估算方法进行了研究，提出了频域与时域相互转换的一般过程；Xu、唐文、张军、关迪等[8-11]研究了结构关键部位动态响应与其振动疲劳寿命之间的关系；白金等[12]提出了一个新的随机振动疲劳损伤参量——多轴振动因子，并利用该因子得到了适用于随机振动下的多轴S-N曲线，给出了一种新的随机振动疲劳的估算方法。

上述文献为直升机机载设备强度校核提供了具体的理论应用条件与操作步骤，但缺乏对设备关重件的随机振动疲劳寿命分析。武器系统工作时，对可靠性要求较高。为了便于设计人员设计，为其提供选型依据，需要对武器系统中的某些关重件进行随机振动疲劳寿命分析。本文将结合直升机振动的特点与结构随机振动疲劳寿命估算方法，提出一种针对直升机机载设备随机振动疲劳寿命估算方法。

1 试验问题分析

1.1 问题描述

按照要求对武器系统进行振动试验，振动分为垂直方向、前后方向和左右方向，每个方向振动4 h。振动类型为周期振动伴随随机振动的混合振动。在垂直方向振动4 h后检测武器各项功能，无异常；继续试验，在前后方向振动3 h 50 min时，武器掉落，用于连接枪身的三颗螺钉断裂。图1所示为螺栓断裂情况。

图1 螺栓断裂

1.2 问题分析

图2所示为被测设备整体模型，图中a处为故障发生处。

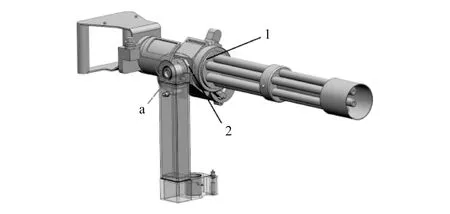
1—武器；2—连接轴图2 整体模型

观察螺栓连接处，发现螺栓圆柱体部分与连接轴存在间隙，螺栓头圆环面与连接轴紧密接触，圆柱体部分与枪身紧密结合，如图3所示。再观察发现，连接轴与武器的连接处存在间隙，且该间隙在设计时不可避免，通过简单受力分析可知，螺栓头与圆柱体拐角处易产生应力集中。

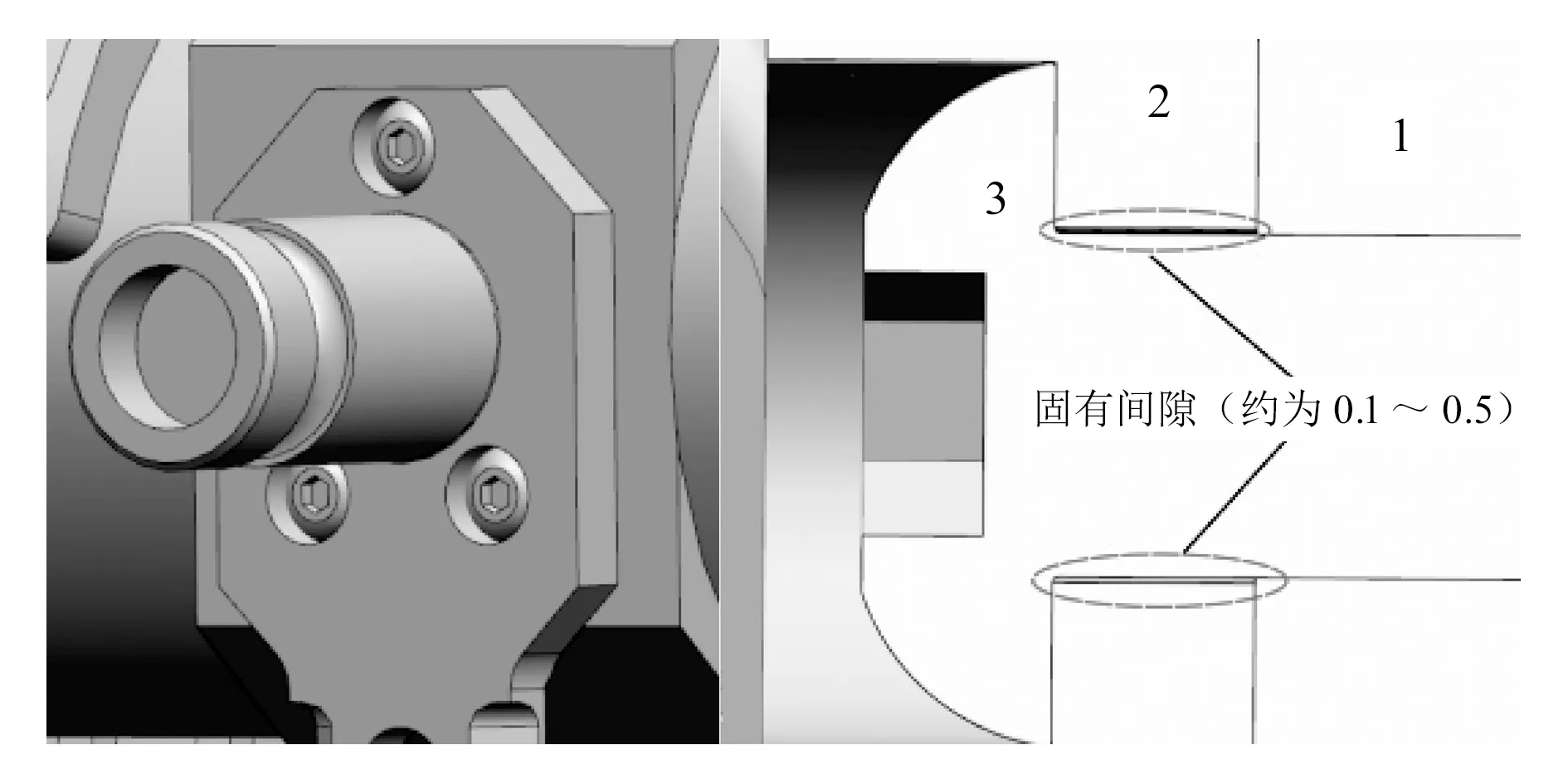
1—武器；2—连接轴；3—螺栓图3 局部a结构

螺栓断裂情况如图4所示，由图可知，武器机械接口处仍留有一截螺栓，说明螺栓螺纹部分的强度是足够的。观察螺栓断裂面，可以看到断裂面贴近螺栓头位置，几乎与第一圈螺纹截面重合。三颗螺栓断裂位置均为螺纹起始位置且断面平整(图中螺纹缺口是拆卸时造成的)，无明显的宏观变形，判断螺栓断裂是疲劳断裂。

图4 螺栓断裂特点

螺栓疲劳断裂在工程中属于常见问题，而在混合振动环境中，对疲劳寿命有要求的结构多是依据工程经验设计以及根据试验结果改进的，这样会增加设计时间与经济成本。为了方便设计人员并节约成本，本文依据试验环境提出了新的疲劳寿命计算方法。

2 建立估算模型

直升机振动由可确定的周期振动与不可确定的随机振动组成。周期振动是由直升机主桨定速转动引起压力场变化而产生的，随机振动主要来自机械不平衡。试验时周期振动与随机振动可以同时施加在被试设备上，而在进行理论计算时，只能单独计算同一种振动类型的疲劳寿命。因此在计算疲劳寿命时，需将周期振动转换为随机振动，这样就可以通过计算随机振动疲劳寿命来代替混合振动的疲劳寿命。

2.1 基本计算方法

本文采用频域法对螺栓的随机疲劳寿命进行估算[7,10]。随机过程的功率谱密度S(f)是一个对称的双边谱，因此可以取一半即单边功率谱密度G(f)来进行研究。在一个平稳的高斯随机过程中，可以用G(f)的各阶谱矩来描述其统计特性，其中第i阶谱矩mi表示如下：

(1)

式中：f为频率。

(2)

式中：m2i为第(2×i)阶谱矩。

当i=2时，称α2为不规则因子，不规则因子可以用于判别随机过程的宽带特性；当α2=0时，随机过程是非常不规则的，趋向于白噪声；当α2=1时，意味着随机过程的每一个峰值过后都伴随着一个低于均值的波谷并与之形成一个循环(类似正弦波)，过程是规则的，对应理想窄带随机过程。

根据随机过程理论可知，随机过程应力峰值为一个窄带高斯过程，所以α2=1。因此,需要计算单位时间内峰值出现的次数νp(频率)和均值正穿越次数ν0(频率)。

(3)

(4)

根据材料的S-N曲线，该曲线可以表示应力循环次数与应力值的关系，如式(5)：

N·sk=C

(5)

式中：N为应力循环次数；s为应力幅值；k与C为材料常数。

结合Miner线性累计损伤理论，可以得到疲劳损伤计算公式：

(6)

式中：D为总损伤；p(s)为雨流幅值的概率密度函数。当D为1时，结构发生破坏，则结构的疲劳寿命T=1/D。

为了方便计算，本文采用Steinberg提出的基于高斯分布和Miner线性累计损伤准则的三区间法则估算部件疲劳寿命，根据该法则可知：

(7)

式中：N1σ,N2σ,N3σ分别为对应区间的应力在材料S-N曲线上所对应的疲劳寿命。

在三区间法则的基础上，对应力幅值的概率密度函数计算区间进行优化，修正了[-3σ,3σ]区间的对应系数[11]，得到：

(8)

2.2 确立边界条件

计算直升机机载结构随机振动疲劳寿命时，关键在于能否正确地将周期振动转换为宽带叠加窄带的随机振动。图5所示为直升机机载设备振动环境试验谱。

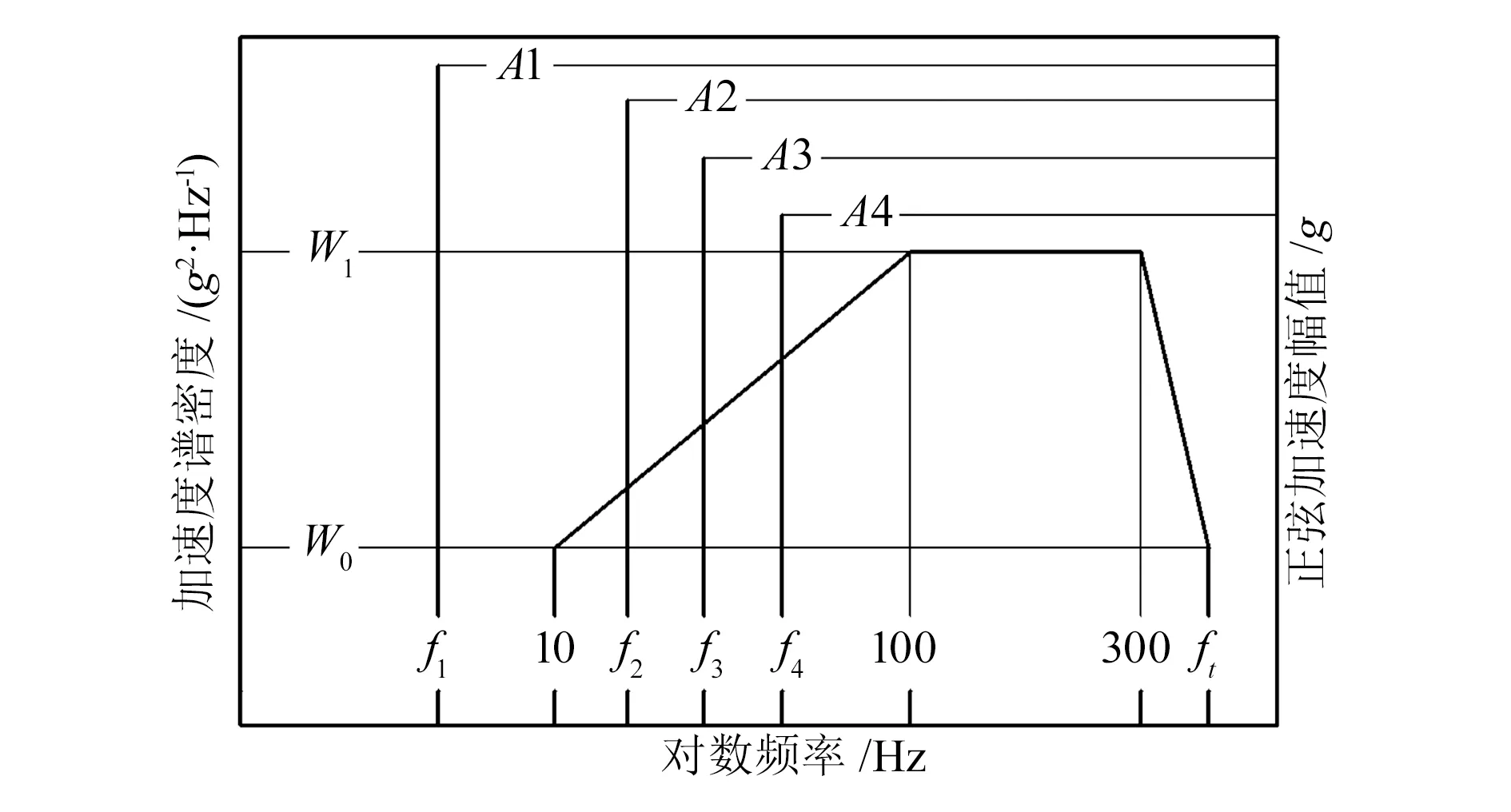
图5 环境试验谱

显然，图5中有正弦加速度幅值与加速度谱密度两种不同的振动谱，因此需要将正弦加速度幅值转换为加速度谱密度，转换公式[13]如下：

(9)

(10)

式中：G为转换后的功率谱密度；B为等效窄带带宽；Afn为对应阶数频率的周期振动峰值；fn为正弦幅值对应的频率；Qfn为品质因数，在试验中获得，本文取10；β为等效因子，一般取值为1.8。

3 仿真分析

3.1 模态与随机振动分析

对直升机振动试验条件进行转换，通过式(9)与式(10)将表1的试验条件转换为表2中的功率谱密度值。

表1 直升机振动试验环境技术条件

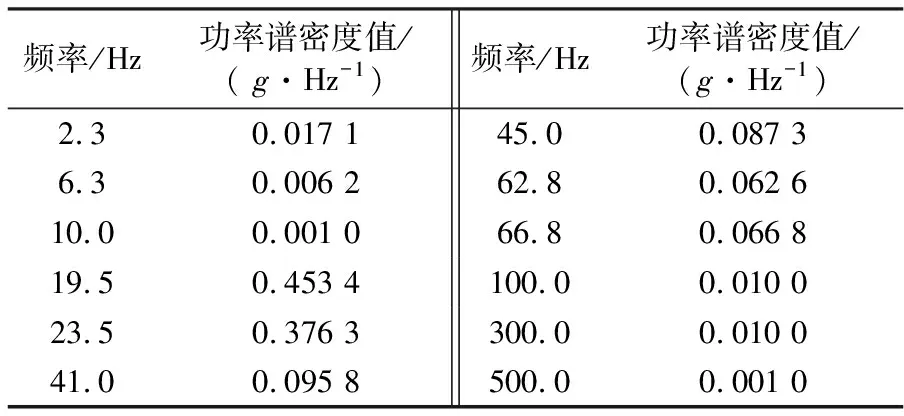
表2 功率谱密度值

确定功率谱密度值后，在有限元软件中依据实际情况对模型的连接关系、材料属性进行设定：枪架底面施加固定约束；螺栓材料为普通碳素钢，密度为7 860 kg/m3，弹性模量为200 GPa，泊松比为0.288，屈服极限为235 MPa，强度极限为407 MPa，疲劳极限为150 MPa。武器质心分布与试验时一致。

对模型进行模态分析，得到模型的振型与振动频率。表3为结构的前10阶模态。

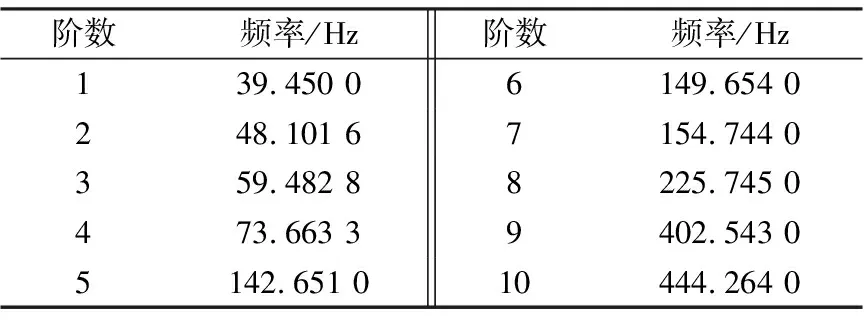
表3 结构的前10阶模态

图6所示为模型的前2阶模态。

图6 前2阶模态

依据表2在有限元软件随机振动模块中添加PSD曲线，沿Z轴方向进行随机振动分析，得到螺栓的等效应力云图，如图7所示，由图发现，最大应力出现在螺栓实际断裂位置附近。

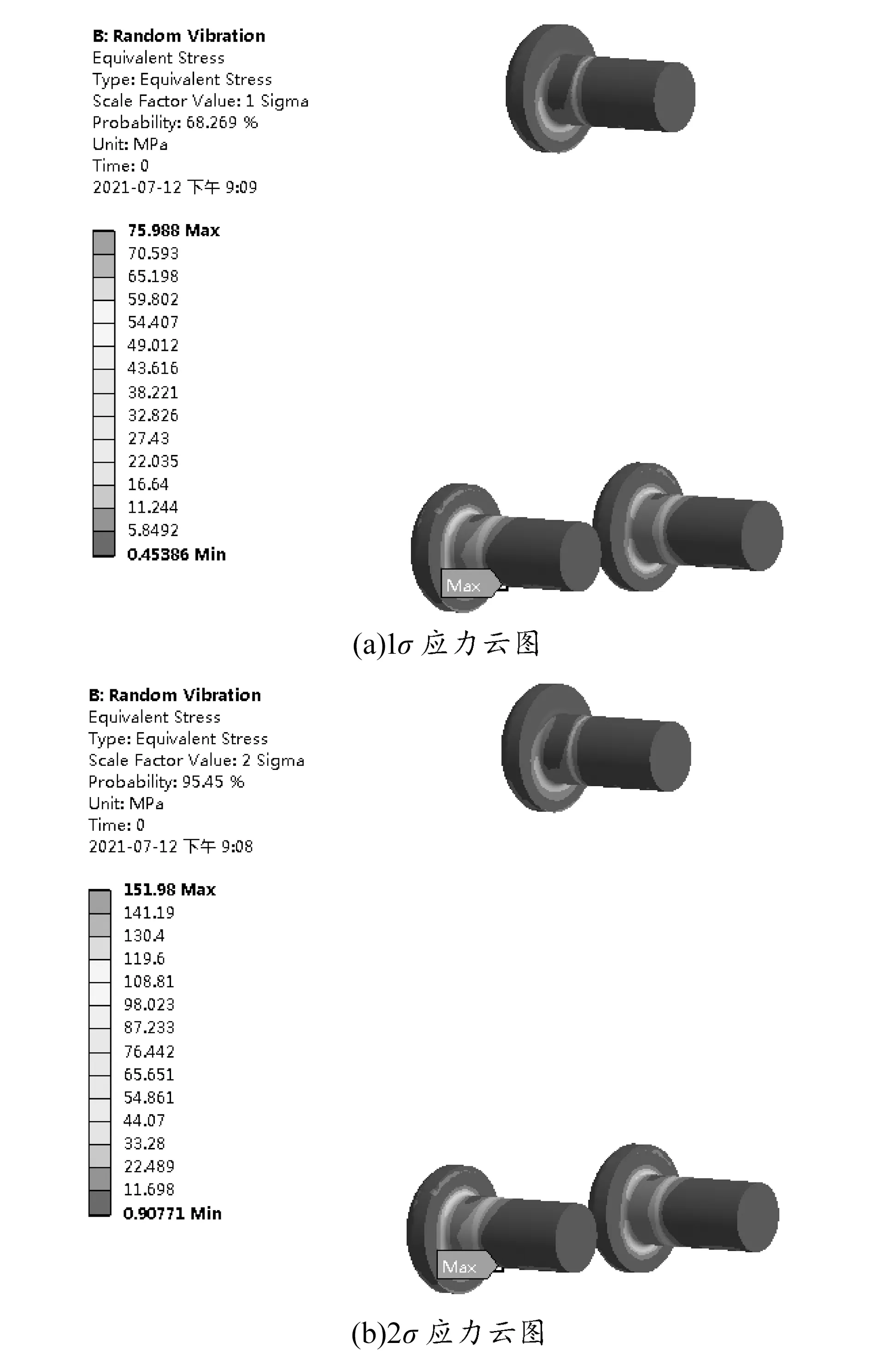
图7 对应区间的应力云图

从图中得到螺栓在各个区间内的应力幅值：1σ区间内应力幅值为75.988 MPa；2σ区间内应力幅值为151.98 MPa；3σ区间内应力幅值为227.96 MPa。

3.2 数值求解

从应力云图中得到螺栓对应区间的应力幅值，每一个应力幅值在材料的S-N曲线上都有唯一对应的最大应力循环次数。如图8所示为普通结构钢的S-N曲线[14]。

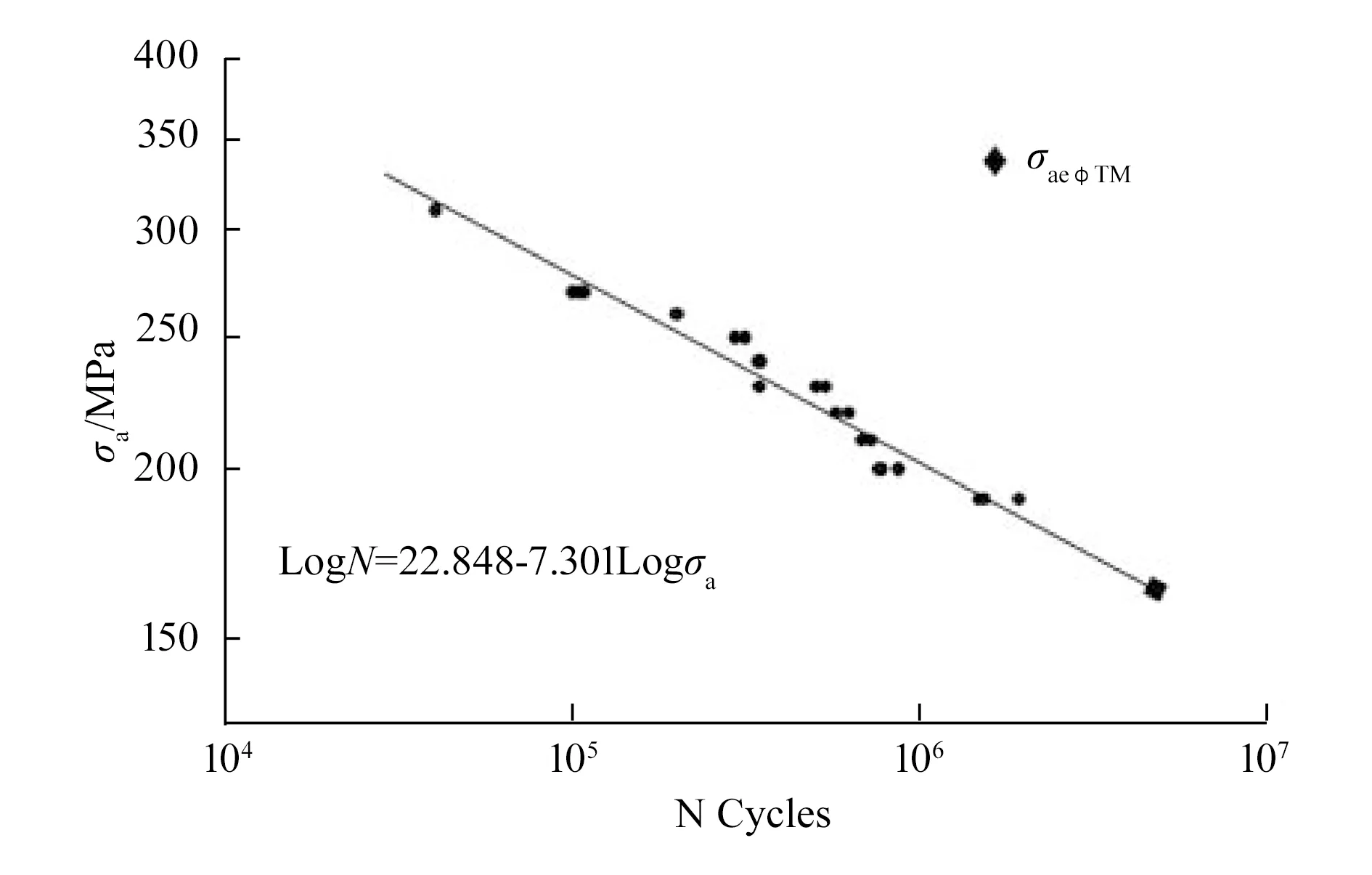
图8 Q235螺栓的S-N曲线

由图8可知，在应力取值区间为1σ时，应力幅值远小于疲劳极限，因此对应的循环次数为无限大；在取值区间为2σ的应力幅值为151.98 MPa时，数值小于疲劳极限，对应的循环次数为无限大；应力取值区间为3σ的应力幅值为227.96 MPa时，对应的应力循环次数为N3σ≈360 000。

结合式(1)计算得到PSD曲线的零阶谱矩m0=354.7、二阶谱矩m2=2.6×107、四阶谱矩m4=19.3×1012。由式(4)计算得到νP=270.7 Hz。

根据式(8)计算得到D=3.374 6×10-5，因此螺栓的疲劳寿命T≈8.23 h。

估算时间与试验发生故障的时间接近，说明该方法能够较为准确地估算螺栓的疲劳寿命，由此也验证了前文的推测，即螺栓断裂为疲劳断裂。

4 结束语

螺栓连接两个部件时，其中一个部件与螺栓圆柱体之间可能会出现大的间隙，造成螺栓拐角处应力集中。从“应力循环-应变位移”角度来看，结构受迫振动时，螺栓可能会产生相当的应变位移，因此关键结构的连接形式为螺栓连接时，应进行疲劳寿命分析。

本文给出了直升机机载设备振动疲劳寿命估算方法，利用该方法对连接螺栓寿命进行估算，得到螺栓的寿命为8.23 h，对比试验结果，误差为5.1%，说明该方法在工程实践中具有一定应用价值，能够为设计人员提供参考依据。但该方法依赖于材料的S-N曲线，而S-N曲线难以适应低周疲劳情况，因此该方法还存在局限性 。