考虑修形、游隙的三排滚子轴承承载分析模型

张远昭，邱 俊，毛范海

(大连理工大学机械工程学院，辽宁 大连 116024)

三排滚子轴承广泛应用于多个领域，如风力发电、矿产开采、隧道挖掘等，该类轴承可同时承受径向力、轴向力、倾覆力矩，具有承载能力大、刚度高，同等承载能力下轴承体积较小等优点，适用于工作环境恶劣、工况复杂、重载等情况。目前，斯凯孚、舍弗勒、铁姆肯等轴承企业在大型轴承研究、设计及生产方面拥有先进的技术，国内对大型轴承的研究起步较晚，相比国际先进水平有一定的差距，因此对大型三排滚子轴承工作可靠性进行分析研究具有重要意义。

国内外对三排滚子轴承的承载性能进行了相关研究，位文明等[1]建立了三排圆柱滚子轴承静刚度矩阵的理论数值分析模型，分析了轴承游隙、外载等因素对静刚度的影响规律；李云峰等[2]针对三排滚子转盘轴承多种失效形式建立了复合载荷下三排滚子转盘轴承的校核计算方法，使用理论模型计算了滚道安全系数、轴承寿命，使用有限元模型分析了轴承的结构强度；姬丽丽等[3]使用非线性弹簧代替实体滚动体建立了转盘轴承有限元模型，分析了三排滚子轴承受载后的载荷分布；Göncz等[4-5]不仅提出了一种用于分析三排滚子轴承滚道承载能力的有限元模型，研究了两种滚动体修形对滚道疲劳寿命的影响，还提出了一种确定大型三排滚子轴承静载能力的计算模型，该模型考虑了滚道变形、游隙等参数的影响，使用矢量方法描述轴承的几何形状，确定出轴承内部的接触载荷分布；冯建有等[6]针对三排滚子轴承基于非赫兹接触理论分析研究了滚道与滚动体之间的接触变形及应力分布规律，使用滚动体与滚道接触有限元模型验证了建立的理论模型。

上述针对三排滚子轴承承载性能的研究忽略了滚动体的修形或轴承游隙等对轴承承载性能影响较大的因素，导致模拟分析的结果不够准确，因此本文提出了考虑滚动体修形与轴承游隙的三排滚子轴承承载分析模型，通过与实体单元模型对比说明了本文所提出的由非线性弹簧组与组合单元结合建立的滚动体-滚道有限元模型的有效性及优势，并采用所提出的模型对某型号风电机组主轴承进行承载性能分析，从而为风电三排滚子轴承游隙与滚动体修形的设计或轴承整体校核提供了一种分析、研究的方法。

1 轴承承载分析模型

1.1 滚动体-滚道几何模型

三排圆柱滚子轴承主要结构参数如图1所示，其中d为轴承内径；D为轴承外径；B为轴承宽度；Dpw1为径向滚动体分布圆直径；Dpw2为轴向下排滚动体分布圆直径；Dpw3为轴向上排滚动体分布圆直径；H为两排轴向滚动体间距；H2为轴向下排滚动体与中心平面的距离。

图1 三排滚子轴承结构参数图

采用对数修形[7]后的圆柱滚子与滚道的间隙如图2所示。当不考虑游隙时，滚动体第j个切片与滚道之间的单侧间隙zkj如式(1)所示；当考虑游隙时，滚动体切片与滚道的单侧间隙需要加上游隙，此时轴承滚动体第j个切片与滚道之间的单侧间隙ZKj如式(2)所示。

图2 滚动体修形与游隙

(1)

ZKj=zkj+0.25(Pa∨Pr)

(2)

式中：Dw为滚动体直径；xj为滚动体第j个切片中心的横坐标；Lw为滚动体长度；Pr，Pa分别为径向、轴向游隙。

滚动体第j个切片与滚道不发生接触变形时的几何条件为ZKj≥0，发生接触变形时的几何条件为ZKj<0。判断公式如下所示：

Pj=0 (ZKj≥0)

(3)

Pj>0 (ZKj<0)

(4)

式中：Pj为滚动体第j个切片的最大应力。

在有限元模型中所建立的滚动体-滚道几何模型如图3所示，滚动体的每一个切片都是用非线性弹簧与组合单元串联进行模拟，非线性弹簧模拟滚动体与滚道之间的接触变形及载荷传递，通过设定组合单元不同的初始间隙来模拟修形滚动体每一切片与滚道之间的间隙。

图3 滚动体-滚道几何模型

1.2 滚动体-滚道力学模型

基于赫兹线接触理论及切片法，将滚动体沿轴线方向切割成长度相同的n个切片，假定在第j个切片与滚道的接触区域中接触应力沿长度方向均匀分布、沿横向为赫兹分布，则第j个切片的最大应力Pj为：

(5)

(6)

式中：qj为第j个切片所受载荷；h为切片的长度；Rj为第j个切片与滚道的等效半径；E1为滚动体弹性模量；ν1为滚动体泊松比；E2为套圈弹性模量；ν2为套圈泊松比。

滚动体切片刚度定义为切片所受载荷与变形量的比值。有限元模型中需要根据已知的轴承尺寸及材料性能等条件设定非线性弹簧组的弹簧刚度，弹簧刚度基于赫兹线接触理论进行求解，求解过程如公式(7)～(9)所示。

Tkij=qkij/δkij

(7)

(8)

(9)

式中：k=1,2,3,分别代表径向、轴向下排、轴向上排滚动体;i代表第i个滚动体；j代表滚动体第j个切片；Tkij为切片刚度；qkij为滚动体切片所受载荷；δkij为滚动体切片的变形；csk为弹性常数；Lwk为滚动体长度；nk为滚动体切片数量。

2 模型对比分析

为了体现所提出的滚动体-滚道模型的有效性及优势，本文使用ANSYS分别建立了单个实体滚动体受压及单个弹簧滚动体受压的有限元模型，并对分析结果进行了对比。滚动体的尺寸、材料、载荷工况信息见表1。

表1 滚动体模型已知条件

两种有限元模型如图4所示，两模型中压块、支撑块及实体滚动体均采用SOLID186单元进行网格划分，接触区域均进行局部网格细化，其中压块、支撑块采用6面体网格，非细化部分网格尺寸为3 mm，细化部分网格尺寸为0.5 mm；实体滚动体采用四面体网格，非细化部分网格尺寸为4 mm，细化部分网格尺寸为0.5 mm。实体滚动体受压模型中接触类型设置为摩擦接触，接触区域中压块、支撑块一侧表面采用TARGE170单元覆盖，滚动体表面采用CONTA174单元覆盖；弹簧滚动体受压模型中修形滚动体采用COMBIN39及COMBIN40单元模拟，非线性弹簧的刚度曲线如图5所示，使用MASS21将弹簧组与压块及支撑块的接触区域耦合。两模型中支撑块底面节点均进行全约束，压块上表面节点均施加竖直向下的均布载荷12 000 N。对两种模型均进行网格无关性分析,最终确定出两种模型的网格节点数分别大于54.69万及26.35万后相邻两组不同网格密度的模型计算得到的滚动体最大应力值相对误差在3%以内，表明两种模型网格节点数大于54.69万及26.35万后滚动体最大应力分析计算结果与网格数目无关。

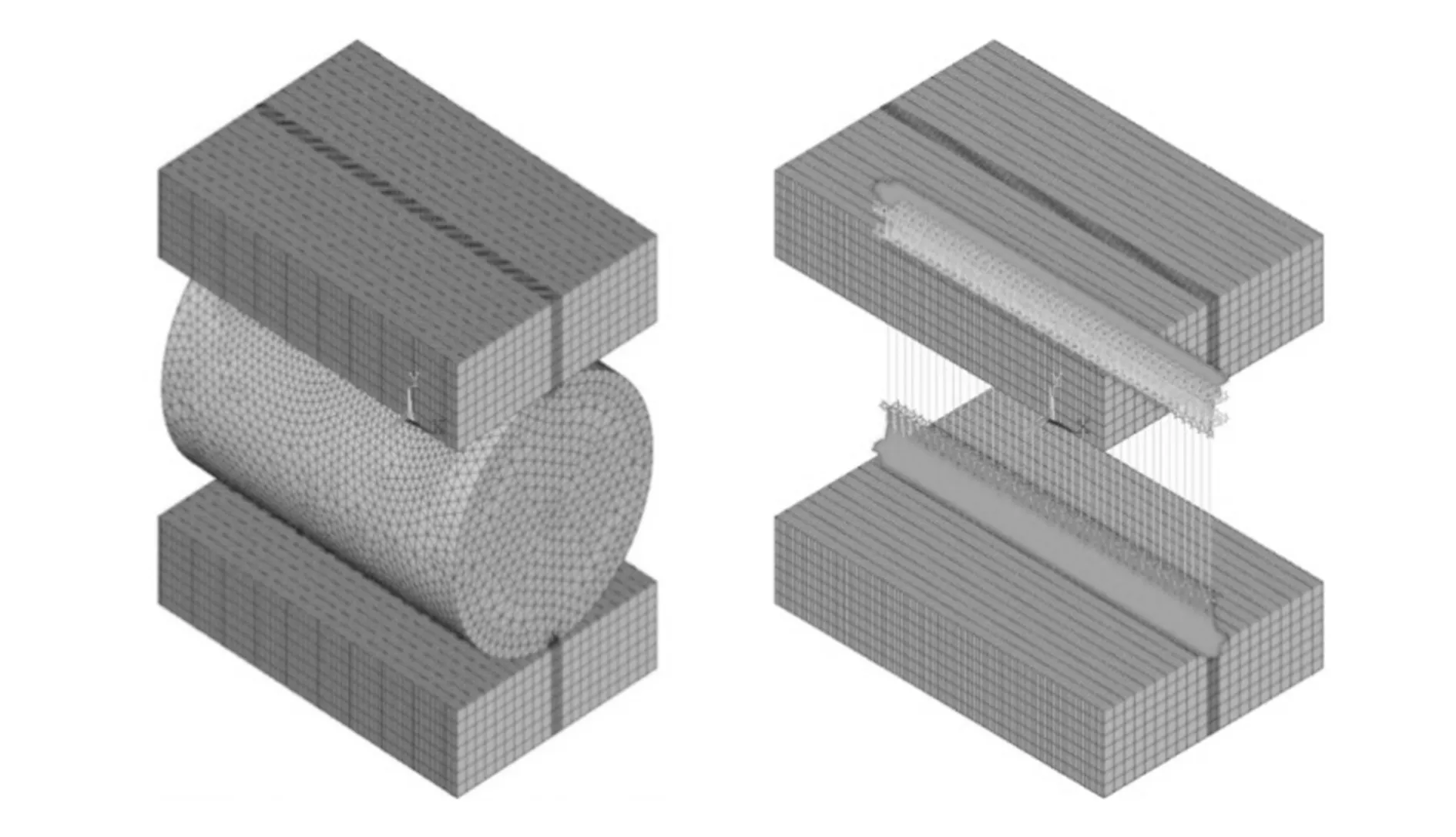
图4 实体及弹簧滚动体受压模型

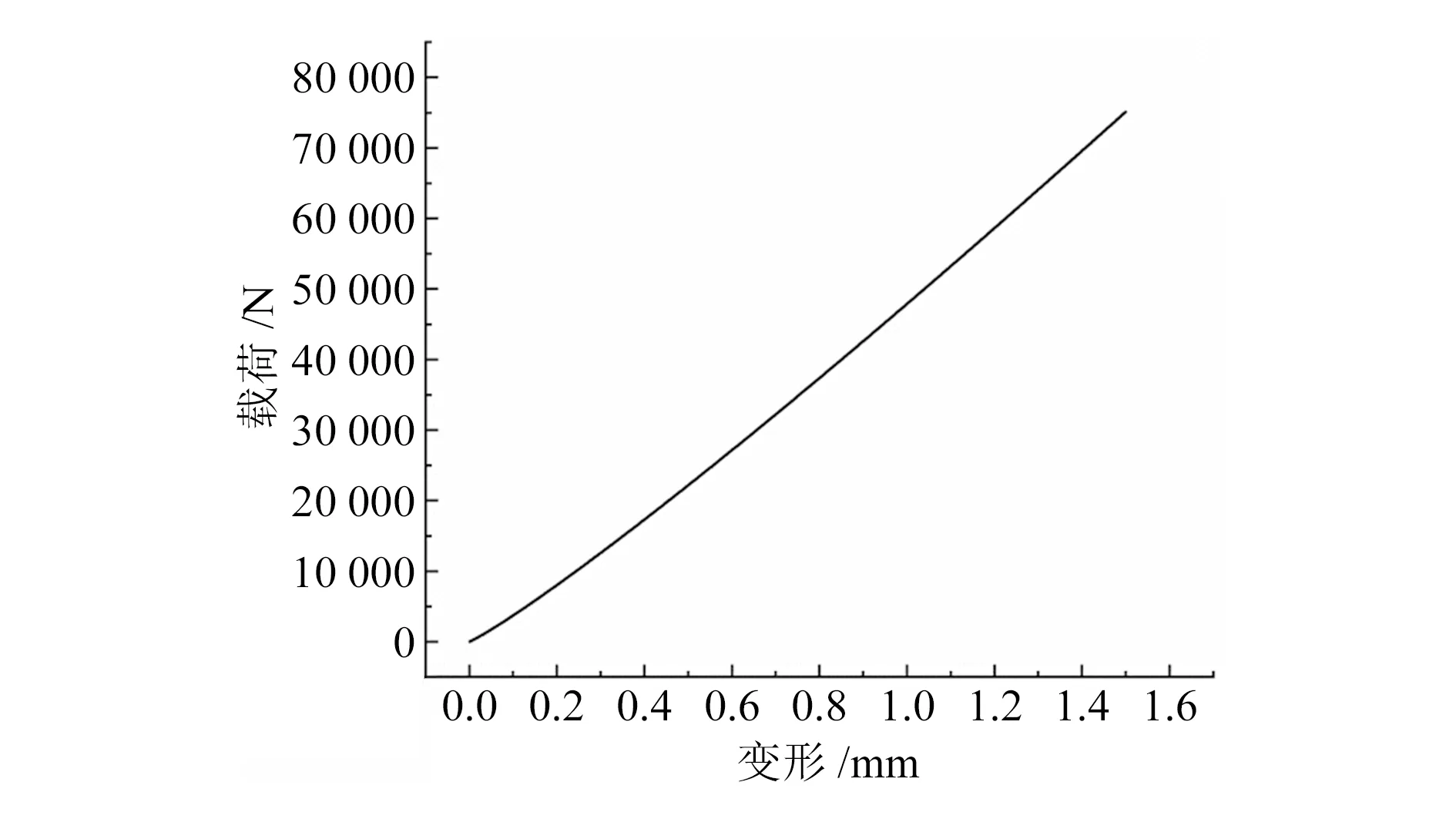
图5 非线性弹簧刚度曲线

两种有限元模型的分析计算结果见表2，滚动体应力分布对比如图6所示。

表2 两种模型分析对比

图6 实体及弹簧滚动体应力分布

上述两种模型计算的应力分布误差在5%以内，但弹簧滚动体模型分析计算所用的时间仅为实体滚动体模型的39%，可见弹簧滚动体模型在保证分析准确性的基础上提高了分析计算的效率，节约了分析计算时间。因此，在建立风电三排滚子主轴轴承整体有限元模型时滚动体采用弹簧滚动体。

3 风电三排滚子主轴轴承分析算例

本文针对某型号风电机组三排滚子主轴轴承建立轴承整体有限元分析模型，对其承载能力进行分析。算例采用的三排滚子轴承其径向游隙Pr=0.3 mm，轴向游隙Pa=0.4 mm，滚动体采用对数修形。其他主要尺寸参数见表3，所受复合载荷见表4。基于轴承整体静力学平衡理论及上述所提出的分析方法所建立的三排滚子主轴轴承承载模型如图7所示，有限元模型如图8所示，整体有限元模型中轴承内、外圈采用SOLID186单元，均设置为4面体网格，内外圈体网格尺寸为25 mm，滚道非接触区域网格设置为8 mm，滚道接触区域细化的网格设置为2 mm；采用COMBIN39单元与COMBIN40单元共同模拟轴承游隙及修形滚动体；弹簧组与轴承滚道节点通过MASS21相耦合；内圈下端面节点全约束；轴承所受外载荷等效作用于轴承外圈几何中心位置处，外载荷作用点与轴承外圈外表面相耦合。

表3 三排滚子轴承主要尺寸参数表

表4 轴承复合载荷表

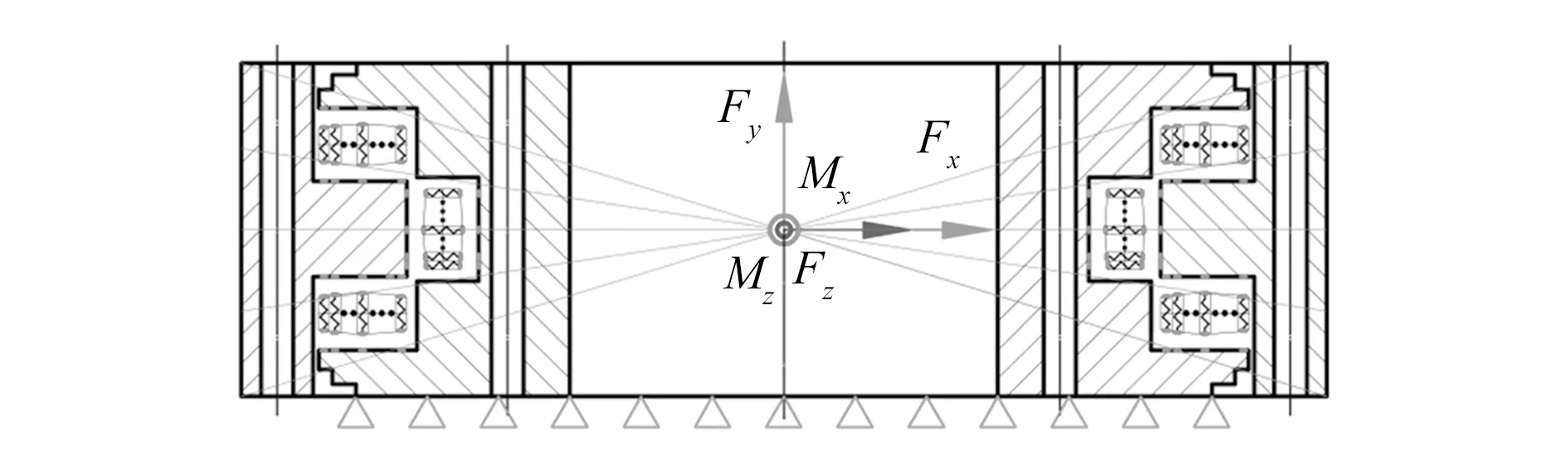
图7 三排滚子轴承承载模型

图8 三排滚子轴承有限元分析模型

三排滚子轴承在复合载荷下的有限元分析计算结果最大载荷和最大应力见表5。分别提取有限元模型中轴承径向、轴向下排、轴向上排滚动体的载荷绘制成轴承受力后的载荷分布，如图9所示，轴承内、外圈的应力云图如图10所示。

表5 有限元模型分析计算结果

图9 轴承载荷分布有限元计算结果

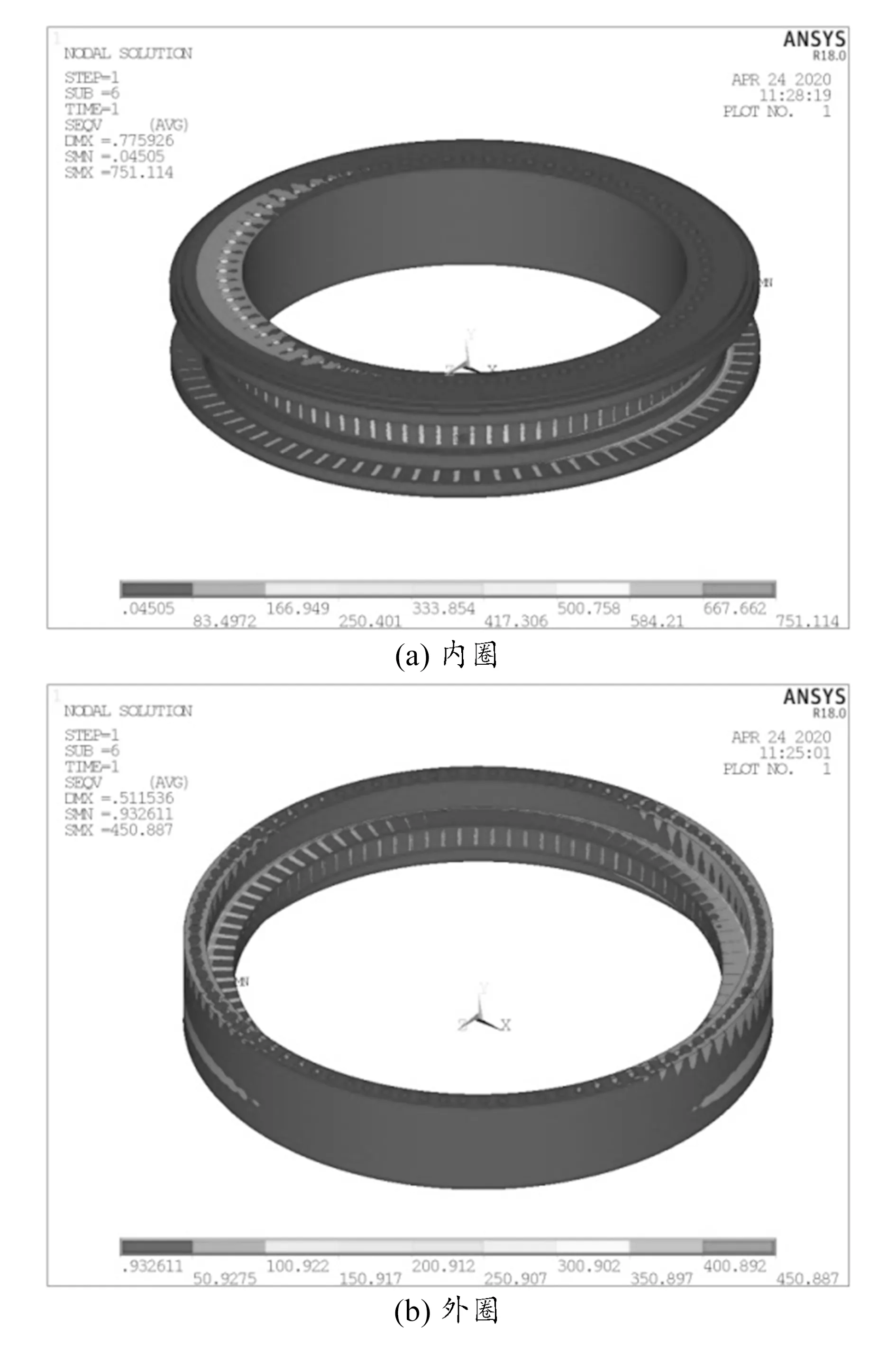
图10 轴承内外圈应力云图

4 结束语

本文提出的考虑滚动体修形与轴承游隙的三排滚子轴承承载分析模型，为风电三排滚子轴承游隙与滚动体修形的设计或轴承整体校核提供了一种分析、研究的方法。实体单元滚动体及弹簧单元滚动体受压有限元模型的应力分布计算结果误差较小，在5%以内；本文所提模型分析所用时间仅为实体模型的39%，证明了滚动体-滚道模型的有效性及优势。对某型号风电机组主轴承进行承载性能分析，得到轴承滚动体最大载荷为353 477 N，最大应力为2 053 MPa。分析计算结果为风电机组主轴承的校核或轴承游隙与滚动体修形的设计提供了理论依据。