基于谐波状态空间的逆变器滤波电路状态评估方法研究

萧声亮,陈文光,刘之戬,郑 亮

(南华大学 电气工程学院,湖南 衡阳 421001)

fit

0 引 言

2022年初某电动车公司宣布召回超12万辆某型号的电动汽车，原因在于部分车辆在使用后会导致元件出现差异使逆变器出现故障，造成逆变器不能正常地控制电流，可能会在行驶过程中发生无法控制车辆的情况从而导致车祸的发生。因此，寻求一个能判断逆变器元件故障的方法[1]，可以有效地防止车祸的发生，同样也能降低检修成本。

据统计，近些年以来，电气设备朝着数字化控制方向发展，而大部分故障却出现在模拟部分。针对如何诊断模拟电路的故障，学者们提出了诸多研究方法[2]，这些研究方法可以大致分为三种基本类型：基于解析模型的方法[3]、基于信号处理的方法[4]和基于机器学习法[5-6]，这三种类型有时会有两两交叉使用[7]，但它们都各自有其优缺点。

基于解析模型的方法是使用系统的分析知识，通常基于使用参数估计[8]、奇偶方程或状态观测器的残差生成[9]。近几年研究重点主要集中在解析模型的鲁棒性问题上[10]，因此数学模型的使用是一个不可缺的关键步骤。X.WU采用两线电压作为诊断变量，提出了一种电压源逆变器多重断路故障的诊断方法[11]。基于信号处理方法是时域[12]或频域。常用小波变换[13]、Park矢量变换[14]和频谱分析等作为工具信号数据，再结合智能方法以此来识别发生故障的类型。L.Ke提出利用三相交流电流平均值提取故障特征，再通过支持向量机对故障进行检测与定位[15]。基于机器学习的方法就是将机器学习技术应用于机器故障诊断[16]。

目前大多数研究学者都聚焦于诊断逆变器开关管和其他元器件的开路与短路这种较为明显故障的研究，对于元器件值细微变化的故障研究较少。导致电容值减小的因素主要有电解电容内部的电解液时间长了会变质干涸，薄膜电容的电极也会发生化学反应慢慢变小等[17-18]。使电感值减小的因素主要有环境的温度发生较大幅度地变化使得电感线圈的外形尺寸因为热胀冷缩而变化，内部磁芯发生了松动，使得介质的导磁性能发生变化，或外部有较强的电磁场干扰等。这两者的变化都是日积月累的，达到一定程度会影响整个逆变器的性能。

滤波电路状态的诊断由于其状态发生改变时，对于电路的影响不同于开路和短路的故障那么明显，故而对于这方面的研究极其稀少。近几十年来，只有少量学者对直流变换器中LC滤波器进行状态诊断。Y.Zheng利用输出纹波电压与电容等效电阻的关系进行状态诊断，还考虑了电感纹波电流的影响，并增加了设置阈值来实现故障的预警。而对于逆变器中的滤波器状态评估，还未有学者对其进行深入研究。

本文采用解析模型与信号处理结合的方法，采用从直流侧注入一定次谐波后查看交流侧端谐波的含量去评价诊断滤波电路数值的变化。

1 谐波状态空间理论

谐波状态空间(harmonic state space，HSS)建模方法最初是为了包含线性化模型的时变点而引入的。由于系统参数的变化特性，线性时变模型实际上是一种非线性模型。因此，该模型难以像线性时不变模型一样在特定的条件下求解。然而，如果假设所有信号都是周期性变化的，则可以通过傅里叶级数将模型线性化。基于上述的假设与定义，谐波状态空间模型可以有式的形式。Xn是状态矩阵，Yn是输出谐波矩阵，Um是输入谐波矩阵。An-m是由线性时变周期理论转换得到谐波系数矩阵，同样Bn-m,Cn-m,Dn-m也是谐波系数矩阵，依赖于输入与输出的数量。所有矩阵的大小取决于在HSS建模过程中考虑谐波的数量。

(1)

每个时变的谐波向量(X、U、Y)都可以用式(2)变换到时域。

x(t)=Γ(t)X

(2)

其中

基于指数函数的基本表示周期调制信号特性，也可以推导出两个信号的导数、积分和乘积等数学表达式，从而得到功率变换器的时变微分方程。时变信号x(t)的导数为：

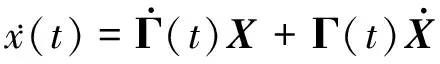
(3)

将式(3)代入式(1)可得：

(4)

其中N为对角矩阵，表示为：

N=dig{-jhω…-jω…0…jω…jhω}

(5)

2 三相LCL型并网逆变器数学建模

2.1 三相LCL型并网逆变器拓扑结构数学建模

电压源型三相LCL型并网逆变器系统结构图如图1所示。

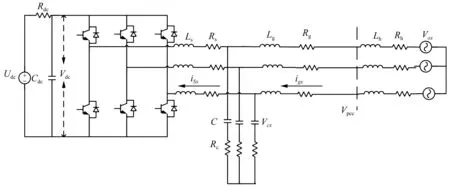
图1 三相LCL型并网逆变器系统结构图Fig.1 System structure drawing of three-phase LCL grid-connected inverter

2.2 三相LCL型闭环逆变器小信号模型

三相并网逆变器的控制框图如图2所示。HSS建模分两部分进行。首先，考虑图1所给的拓扑图，建立小信号的HSS拓扑状态方程。其次，如图2所示中的控制器部分是通过线性时不变周期理论建模成的。

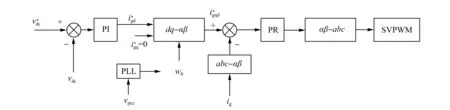
图2 逆变器闭环控制框图Fig.2 Inverter closed loop control block diagram

2.2.1 拓扑结构建模

根据图1的拓扑图可得三相逆变器的小信号模型为：

(6)

其中

(7)

(8)

式中：R1=Rc+Rs;L2=Lg+Lh;R2=Rh+Rg;u=3×(2h+1),v=1×(2h+1)，h为HSS模型考虑的最高频次；Γ[Sa]、Γ[Sb]、Γ[Sc]分别为开关函数sa、sb、sc傅里叶系数所构成的(2h+1)×(2h+1)阶拓普利兹矩阵；Γ[W]=[Γ[Sa],Γ[Sb],Γ[Sc]]；Γ[G]=Γ[W]-Γ[Sa+Sb+Sc]/3×[Ev,Ev,Ev]T。其中获得SVPWM开关函数的方法可以采取双变量傅里叶变换获得，其A相的开关函数展开式为：

(9)

式中：M为调制比，M3为SVPWM三次谐波含量，ωo为调制波角频率，ωc为载波角频率，Dmn的具体表达式为：

式中：Jn(x)为第一类贝塞尔函数，其表达式为：

(11)

2.2.2 控制结构建模

控制模块主要有低通滤波器、PI控制器和PR控制器，根据流程图可得逆变器控制部分HSS的状态方程：

(12)

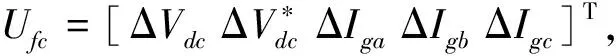
(13)

(14)

(15)

其中Cf1=-KpKpPRΓ[cosθ]

Cf2=KiKpPRΓ[cosθ]

(16)

其中

其中各参数都与状态变量相对应，如Kp和Ki分别为PI控制器的比例与积分的增益，KPRα1、KPRα2、KPRβ1、KPRβ2分别为PR控制器的在旋转坐标的增益系数，KLPF为电压低通滤波器的增益系数。

由此，逆变器闭环中的拓扑及控制模型已经建立完毕，拓扑结构和控制结构之间的小信号关系如图3所示。

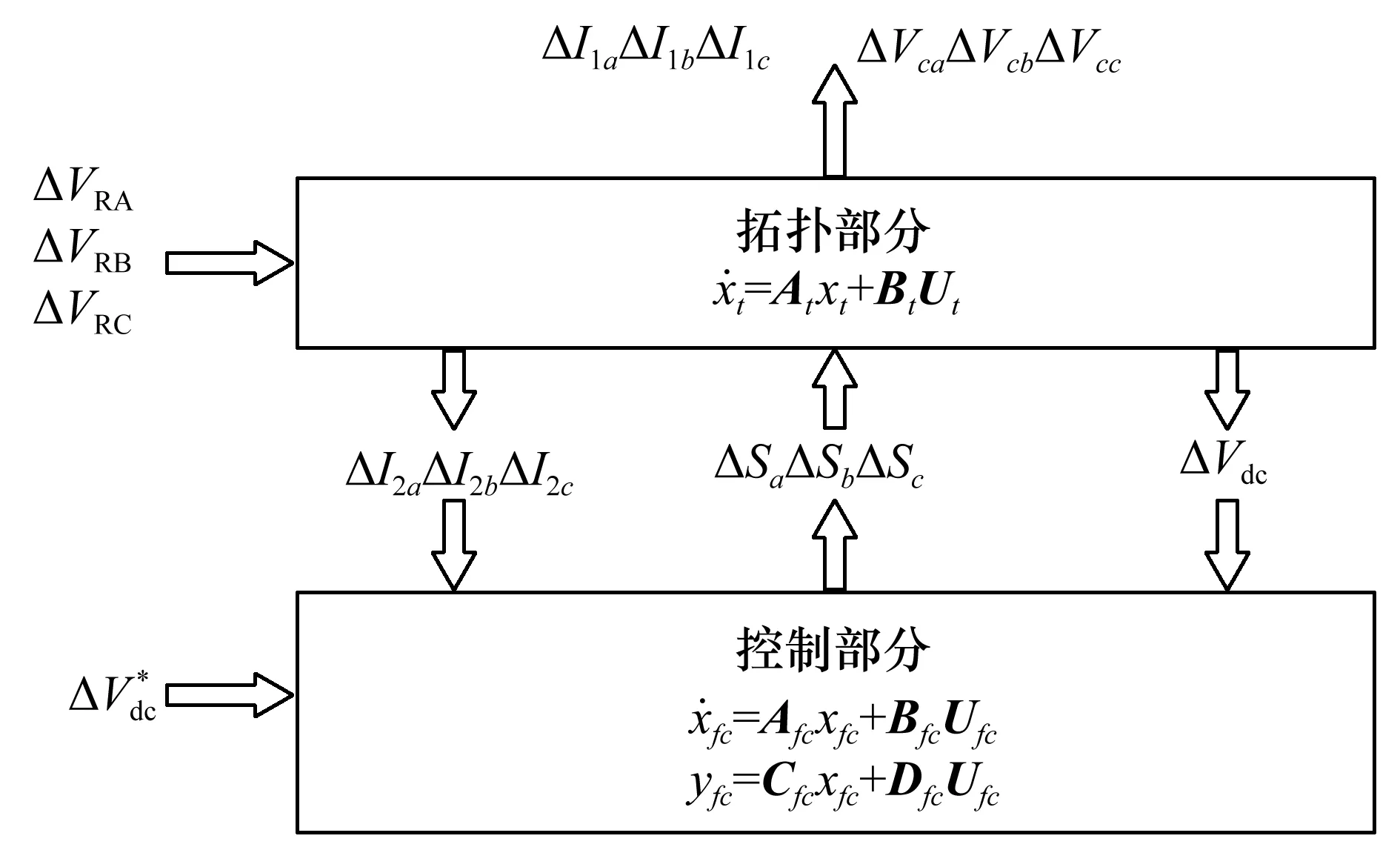
图3 逆变器小信号之间的关系Fig.3 Relationship among inverter small signals

2.3 谐波传递函数

为研究输入量与输出量之间的耦合关系，需要将HSS方程化简为谐波传递函数。通过状态空间方程与传递函数之间的转换关系，可得：

(17)

令

H(s)=Γ[C](sI-Γ[A]+N)-1Γ[B]+Γ[D]

(18)

式中：H(s)为谐波传递函数矩阵。相较于线性时不变模型，HSS模型可用于研究不同频次谐波间的传递关系。可将H(s)定义为：

(19)

式中：矩阵元素为耦合系数，且都为复数。当式中s=0时，通过对矩阵进行截断，可获得稳态时输出变量与输入变量间的耦合系数阵。

2.3.1 直流电压对输出的耦合特性影响

这里取最高谐波展开次数为33和载波比为15作为分析研究，MATLAB软件中的函数ss2tf能指定某个输入对于输出的传递函数关系，在设置输入为直流电压，可获得如图4所示的直流电压输入与各输出谐波之间的关系。从图4中可能看出，直流侧电压与其并联的电容电压0次谐波的耦合度最高。

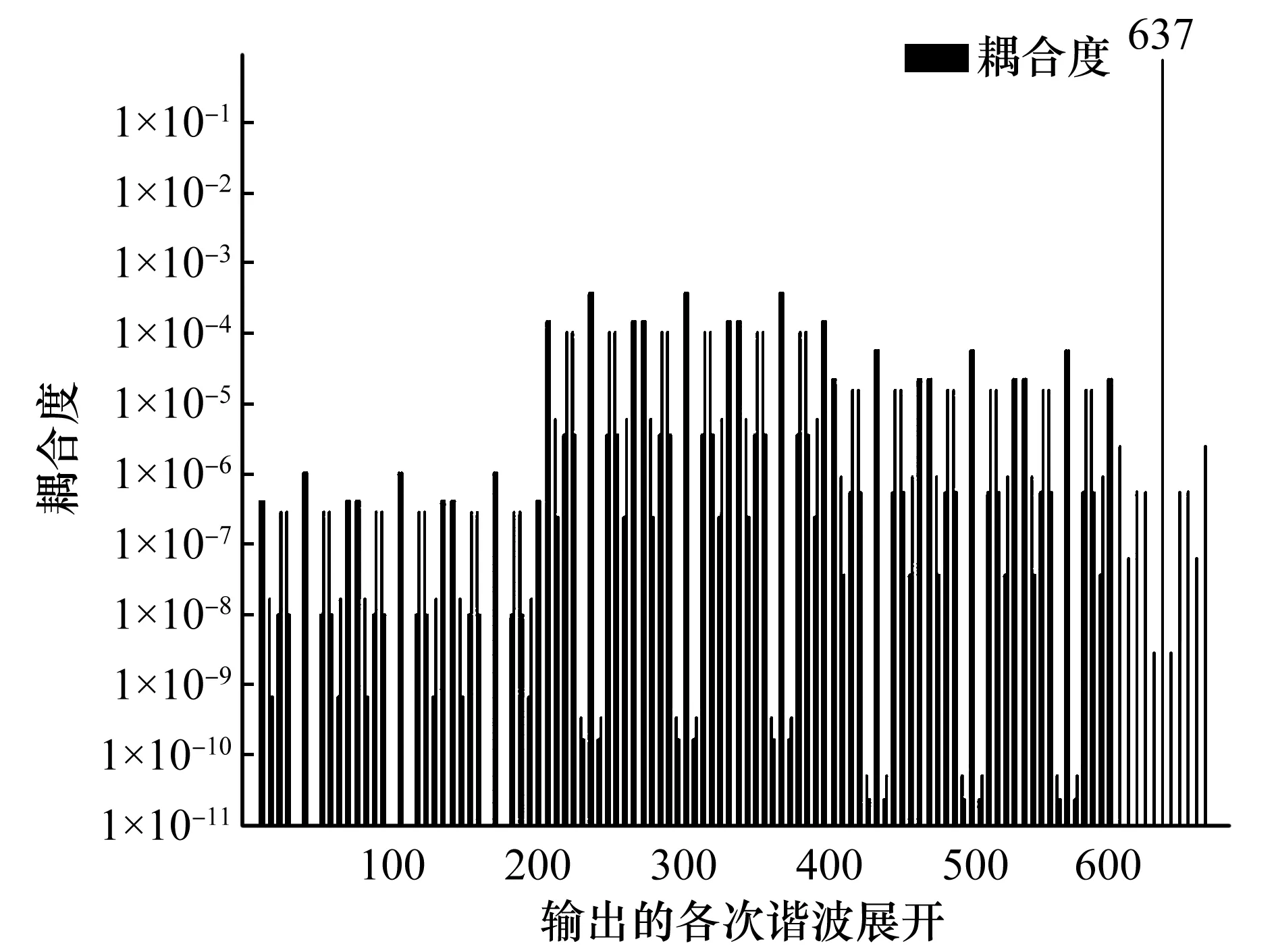
图4 直流电压输入与输出谐波的耦合关系Fig.4 Coupling relationship between input and output harmonic of DC voltage

为了更清晰地看出直流侧电压与谐波耦合性的关系，这里对A相逆变器侧电感电流谐波进行展开，如图5所示。从图5中可以看出直流电压源对逆变器侧电感电流的1次、13次、17次、29次、31次和其相对应的负次谐波耦合度较高，从数字可能看出直流电压源对奇数次谐波的耦合度较大，而对于偶数次谐波的耦合度较小。同理图6为直流电压源对输出电流的耦合度，从图6中可以看出其耦合度与逆变器侧电流各谐波的耦合度规则一样，不同的是直流电压源对逆变器侧电感电流整体的耦合度都比输出电流的耦合度高。对此可以得出结论，离输入越近的输出耦合性越高。

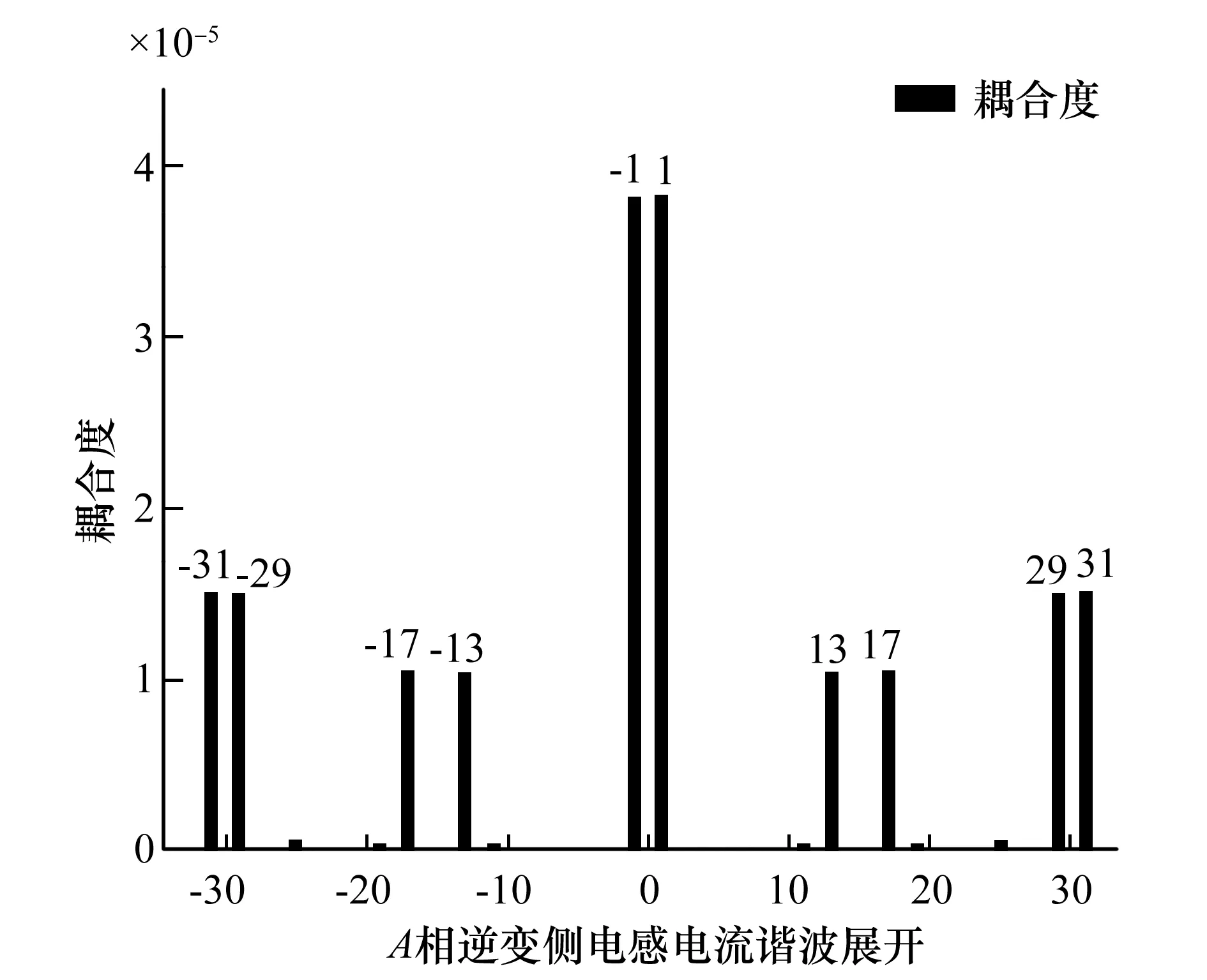
图5 直流电压输入与A相逆变器侧电感电流的耦合度Fig.5 Coupling degree between DC voltage input and inductance current on A-phase inverter side

2.3.2 直流电压扰动对并网电流的耦合特性影响

频率为250 Hz时在直流侧电压中给定五次扰动电压(峰值为37.5 V),观察与输出电流谐波的耦合情况。从图7可知，当给定5次扰动时，其输出侧谐波在4次和6次谐波上耦合程度较高，其次是-8次、-12次和18次、22次。根据多个实验可以得出如下规律，当向直流侧注入k次扰动时，输出电流会由k±1次的两个耦合分量，其次k±13、k±17、k±29和k±31等较小的耦合分量，可以看出与直流电压输入的规律一致。由于若引入正负序电流的概念，则当注入k次扰动时，输出侧会产生k-1次的负序电流和k+1次的正序电流。因此为了便于分析，本研究将耦合度正负符号进行去除。

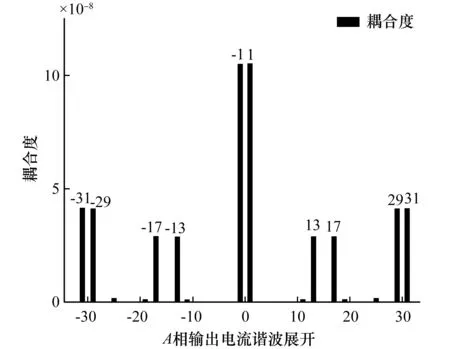
图6 直流电压输入与A相输出电流的耦合度Fig.6 Coupling degree between DC voltage input and A phase output current

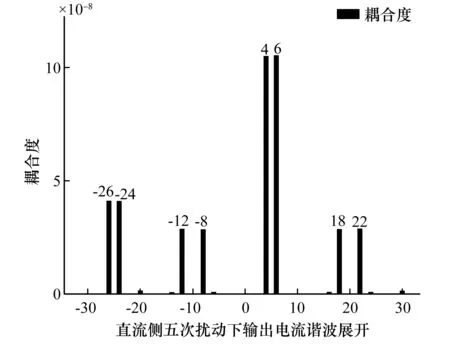
图7 直流侧五次扰动下与输出电流的耦合度特性Fig.7 Coupling degree characteristics of output current under five disturbances in DC side

2.4 滤波电路与谐波的耦合特性分析

为了减小载波比太小导致电流的低次谐波过高，而太高的载波比运行时间又比较长，考虑两方面因素设置载波比为30，最高次谐波为60，来研究电感电容对输入与输出的耦合特性影响。

1)输出侧电感值对耦合特性的影响

考虑在保持其他参数不变的前提下改变输出侧电感值时，研究输入直流源与输出电流一次谐波的耦合关系，MATLAB仿真结果如表1所示。

表1 输出侧电感值对耦合特性的影响Table 1 Influence of output side inductance value on coupling characteristics

2)逆变器侧电感值对耦合特性的影响

考虑在保持其他参数不变的前提下改变逆变器侧电感值时，研究输入直流源与输出电流一次谐波的耦合关系，MATLAB仿真结果如表2所示。

表2 逆变器侧电感值对耦合特性的影响Table 2 Influence of inverter side inductance value on coupling characteristics

3)逆变器侧电容值对耦合特性的影响

考虑在保持其他参数不变的前提下改变滤波电容值时，研究输入直流源与输出电流一次谐波的耦合关系，MATLAB仿真结果如表3所示。

表3 逆变器侧电容值对耦合特性的影响Table 3 Influence of inverter side capacitance on coupling characteristics

从表1到表3中可以看出，滤波电路的元件值的改变或多或少影响着输入直流电压与输出电流的耦合关系。而单从正常参数的一次谐波的耦合度来看，载波比的增大能够大幅度地降低谐波含量的大小。通过前几节分析可得，正常情况下直流电压源0次谐波会在输出电流中产生一个一次的正序电流一个一次的负序电流，这会增加在50 Hz的输出电流中寻找故障的难度。因此可以考虑逆变器正常情况下，对谐波耦合性差的区域注入一定频率的谐波扰动，继而观察输出电流这个频率旁的耦合性判断逆变器是否发生故障。这里将扰动电压设置幅值为50 V频率为500 Hz。

当系统在注入k次谐波扰动时，电感电容的变化都会一定程度地影响输出电流k-1次谐波的耦合度。耦合程度与谐波含量存在正相关关系，当设定一个耦合度临界值，一旦电感电容值出现难以承受的故障进而引起耦合度超过设定的临界值时，就可判断滤波电路的电感电容元器件值是否发生改变。

2.5 故障曲线拟合

通过仿真不断地减小电容值，获得输出电流的9次谐波含量值并画出如图8所示的散点图。从图8中可以看出其值近似成线性状态，通过线性拟合可获得电容值与谐波含量的近似拟合曲线。这里共采样了26个点，每隔0.5 μF去一个输出电流的9次谐波含量值。图8中散点图及线性拟合是oringin软件所绘制，其所得到拟合的线性方程中包含残差平方和及R平方。

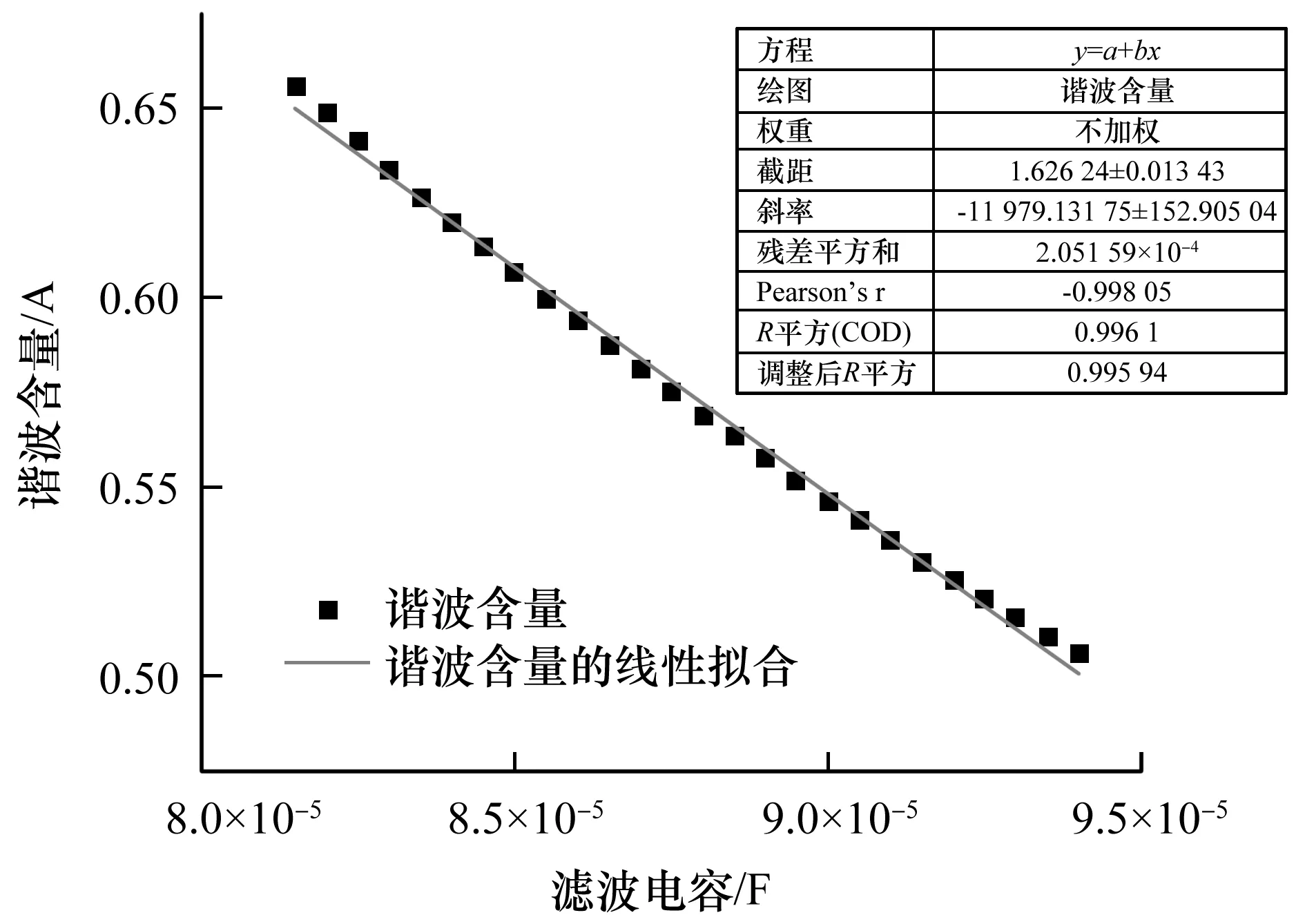
图8 输出电流9次谐波含量随滤波电容值改变的关系图及拟合曲线图Fig.8 Scatter diagram and fitting curve of the 9th harmonic content of the output current with the value of filter capacitance

由电容值变化的散点图，可以得出输出电流9次谐波含量随滤波电容值的拟合曲线可近似表示为：

yC=1.626 24-11 979.131 75xC

(20)

同理获得如图9和图10的输出电流9次谐波含量随逆变器侧和输出侧电感值的散点图及拟合曲线图，其拟合曲线可近似表示为：

yL1=1.358 87-137.462 51xL1

yL2=0.935 61-129.561 26xL2

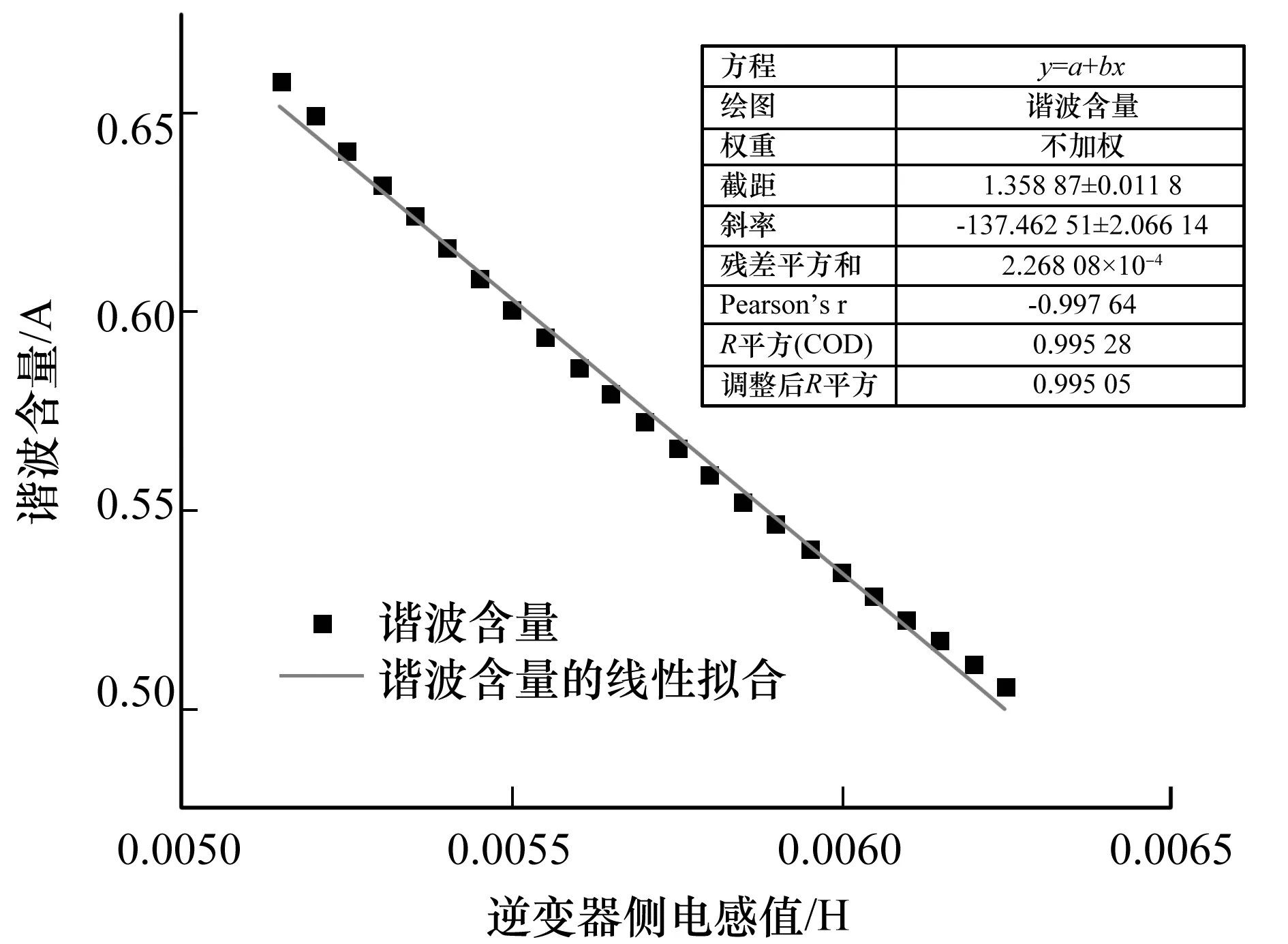
图9 输出电流9次谐波含量随逆变器侧电感值改变关系图及拟合曲线图Fig.9 Scatter plot and fitting curve of the ninth harmonic content of the output current with the inductance value of the inverter side

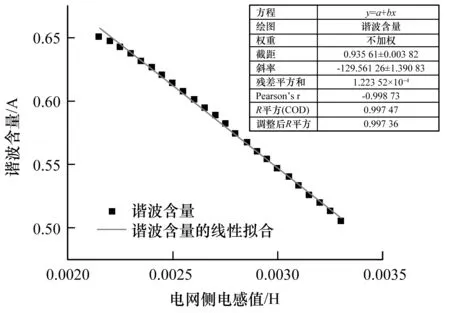
图10 输出电流9次谐波含量随输出侧电感值改变关系图及拟合曲线图Fig.10 Scatter plot and fitting curve of the ninth harmonic content of the output current with the inductance value of the output side

为验证其拟合曲线的准确性，将在此阈值的区间中随机找几个不参与拟合曲线的点去验证其准确性。例如这里取滤波电容88.35 μF，通过仿真获得其输出电流9次谐波含量为0.564 88，同时将滤波电容值放到拟合曲线中计算可得其因变量为0.567 88，两个值误差0.003。经验证去拟合曲线的拟合程度和可靠性都较高。

从上述的分析可以知道，在一定区间范围内滤波电容电感值的变化与输出电流9次谐波含量呈近似的线性关系。而且其三个拟合曲线都呈现反相关，其中滤波电容的相关系数较大。

3 实验验证

为进一步验证所提方法的有效性，本研究搭建了75 V直流输入30 V交流输出的样机，这里滤波电路的各参数为L1=1 mH，L2=680 μH，C=10 μF。设置逆变器的开关频率为30 kHz，注入峰值3 V频率为500 Hz的扰动电压，其逆变器的逆变桥实物如图11所示，整机测试带16 Ω负载波形如图12所示。并对波形图的数据进行傅里叶变换，得到各谐波的含量，如图13所示。将L2的电感换成470 μH，重新注入500 Hz扰动获得波形参数，经过傅里叶变换其分布如图14所示。

图11 逆变器的逆变桥实物图Fig.11 Physical map of inverting bridge of inverter

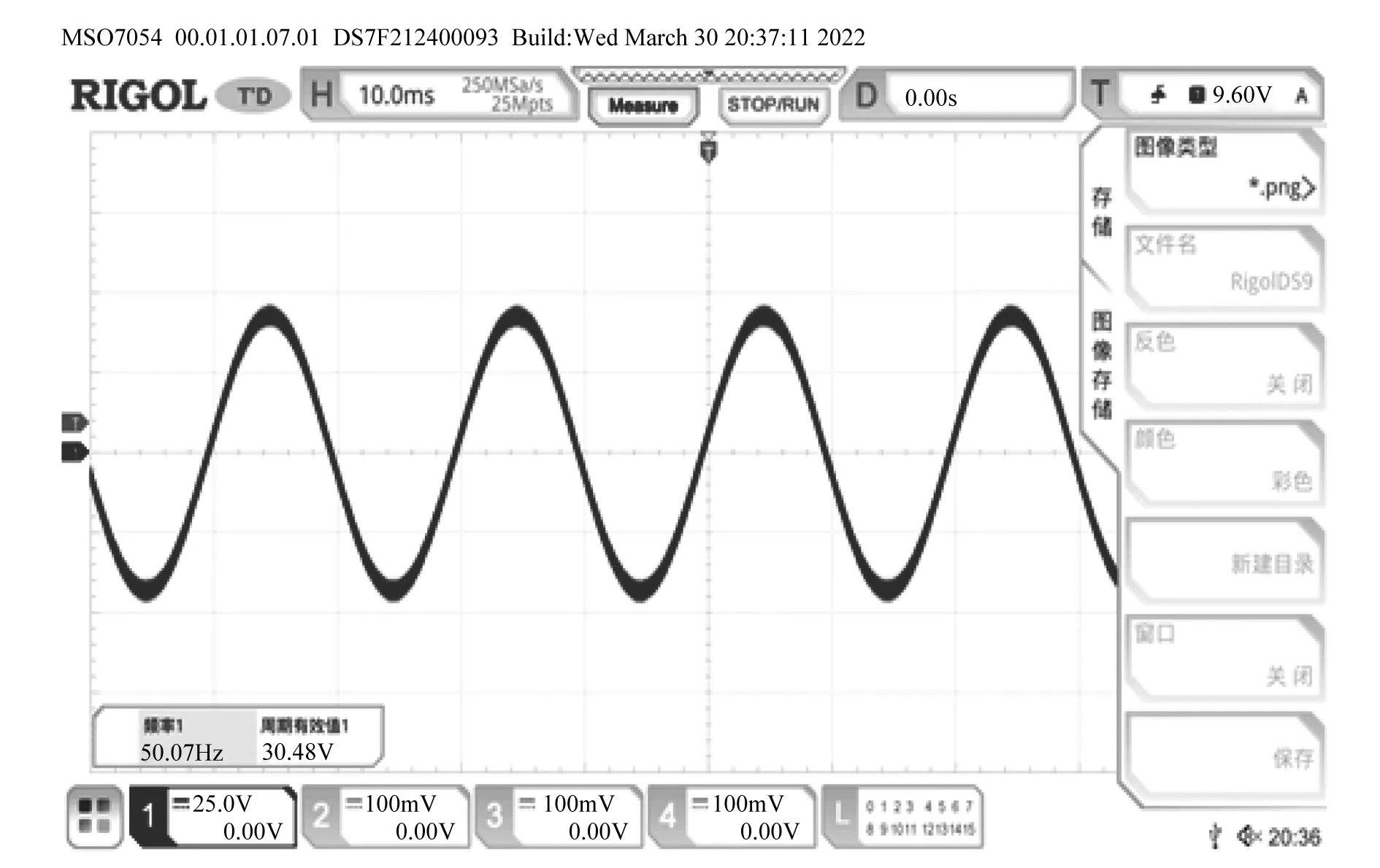
图12 直流电压10次扰动下A相电压波形Fig.12 A-phase voltage waveform with 10 perturbations of DC voltage

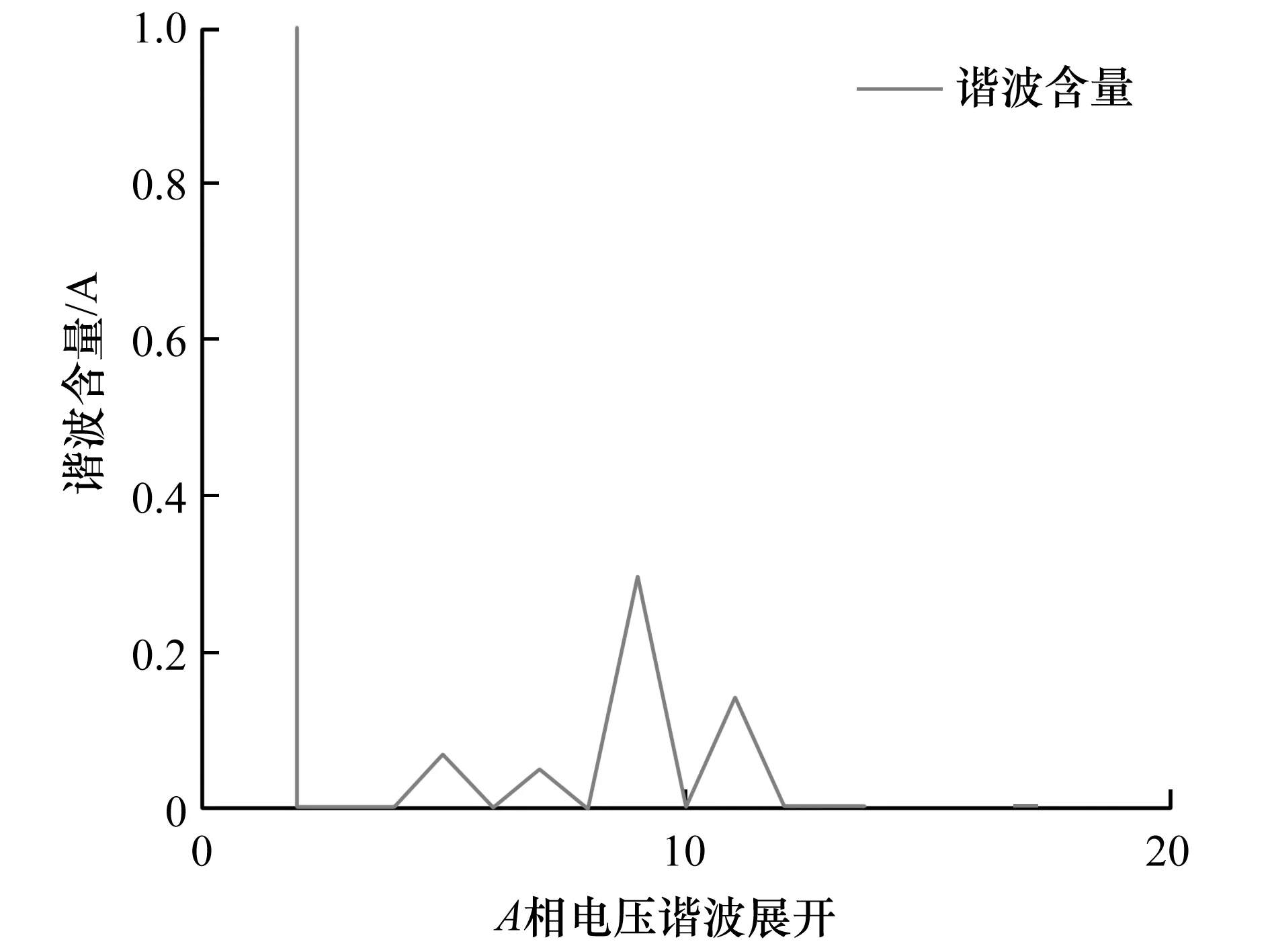
图13 L2=680 μH时直流电压500 Hz扰动下的电压谐波Fig.13 Voltage harmonics under 500 Hz disturbance of DC voltage when L2=680 μH

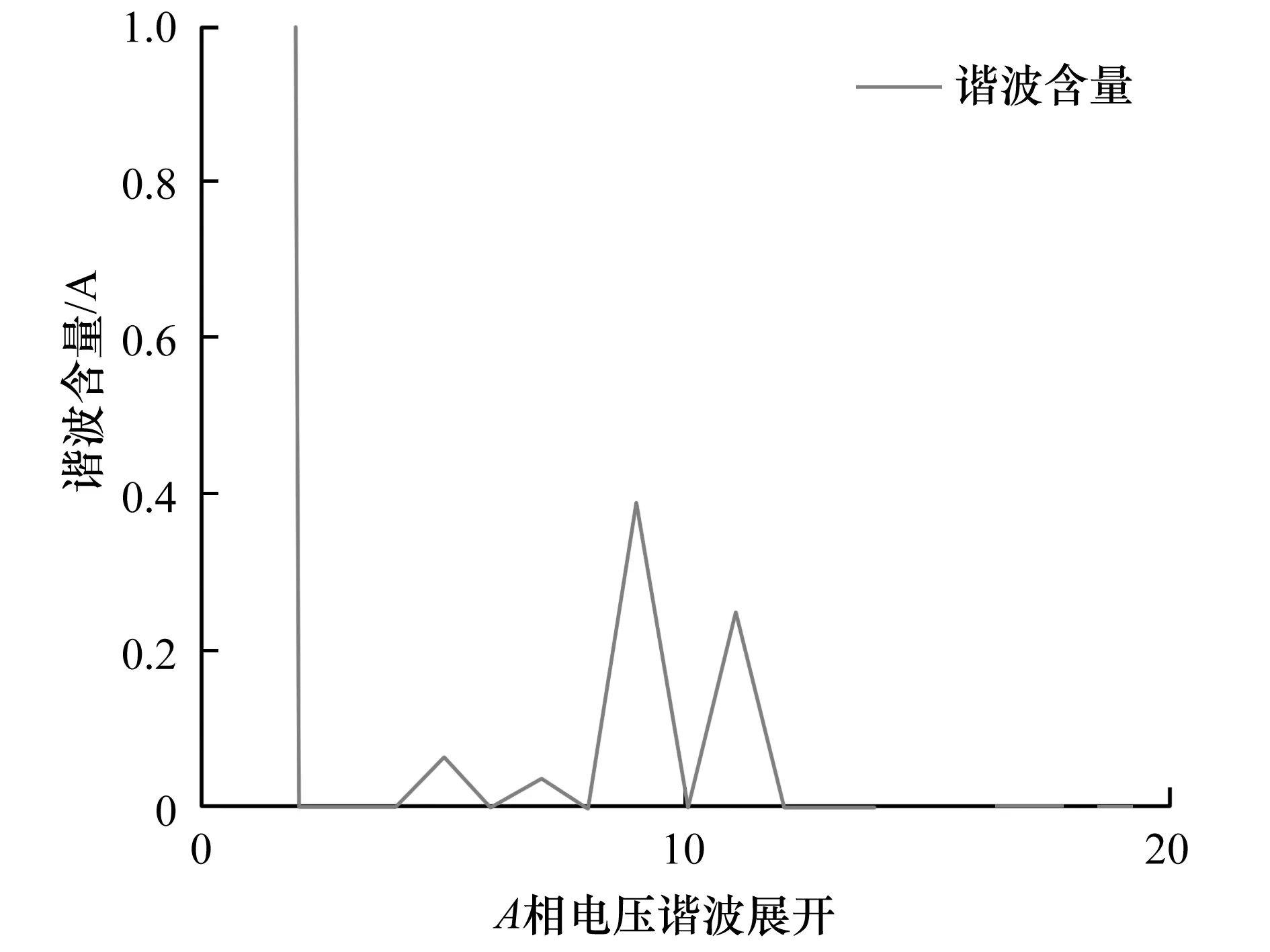
图14 L2=470 μH时直流电压500 Hz扰动下的电压谐波Fig.14 Voltage harmonics under 500 Hz disturbance of DC voltage when L2=470 μH

从实验结果看出，直流侧注入扰动会产生其两侧的正负谐波，且滤波电路元件的变化会改变注入扰动后产生的谐波含量，验证了建立的模型和仿真模型得到的结论的正确性。

4 结 论

逆变器逐渐普及到人们的生活中，逆变器各谐波之间的关系也成为国内外研究学者的关注热点。本文以LCL型三相逆变器研究对象利用谐波状态空间理论建立数学模型，得到如下结论：

1)注入直流侧的k次扰动，输出端会获得k-1次负序谐波和k+1次正序谐波，次级谐波分量会分布在基波和载波的奇数次和的区域；

2)滤波电路的元器件值的大小会对耦合度产生影响，元器件值越小耦合度越小，元器件值越大耦合度越大。并给出元器件值与谐波之间变化拟合成线性曲线的方法，并验证了其正确性。

通过以上结论，利用注入法观察输出电流谐波的大小去诊断逆变器滤波电路元器件值降低的程度。