改进的Chan-Taylor 加权室内定位算法研究∗

方李林 王建新 张 汉

（西安科技大学 西安 710600）

1 引言

位置服务现逐渐渗透到人类生活的各个方面，目前室外有定位技术已经很成熟的全球定位系统（GPS）以及蜂窝移动网络［1］。室内有多种定位技术，主要有Wifi 定位、蓝牙定位、RFID 定位、Zig⁃bee 定位和超宽带定位技术等［2］。在复杂的室内环境下，存在多径，噪声及非视距（NLOS）的影响，导致其定位精度有所下降［3］。超宽带（UWB）系统利用纳秒或亚纳秒级的窄脉冲进行信号传递，UWB无线通信技术以其短距离无线通信中的绝对优势，在室内定位中应用极其广泛［4］。

国内外对于复杂的室内超宽带（UWB）定位研究主要分为两大类［5］，一个是视距环境（LOS）与非视距（NLOS）路径的鉴别和非视距误差的抑制，另一大类就是多种算法协作定位［6］。在国内郑茜颖等人在知道先验信息的情况下对路径进行鉴别，在未知路径下进行卡尔曼滤波来提高定位精度［7］。肖竹等利用TOA 估计算法对最强路径进行鉴别并降低NLOS 误差［8］。文献［9］将Chan 算法和卡尔曼滤波算法进行协作定位，来提高定位精度。国外，Kim D H 等通过测量信号强度来识别NLOS，实验结果表明该算法在UWB 信道环境中有效识别了NLOS［10］。Qi Y 等通过统计数据区分视距与非视距传播路径，利用多径分量估计信号的TDOA 进而实现定位，实验研究发现多径分量的强度与NLOS 延迟方差影响定位的精度［11］；Guvenc I 等提出了用联合似然比方法，并分析了三种不同加权最小二乘定位技术，实验证明了算法的NLOS 高识别率［12］。

Chan 氏算法对信道比较敏感，不需要初始值，在噪声服从高斯分布时有较高的定位精度。当在复杂的室内环境下时，存在一些NLOS 的影响从而导致定位精度下降。而Taylor 算法过于依赖初始值，但是在实际环境中，初始值的选取具有一定的难度。所以本文通过CHAN、CHAN-Taylor 分别获得估计值，对两次估计值进行加权得出最终标签位置估计。取长补短，不仅延续了Chan 算法计算量小的特点，而且继承了Taylor 算法的精确性和鲁棒性。

2 Chan算法

当信道满足高斯信道时，LOS 环境下Chan 算法有良好定位精度，但是在实际复杂的室内环境中，难免会存在一些NLOS 的影响导致定位精度降低，因此在室内定位中它一般与其他的算法协同定位。其基本原理是利用两步加权最小二乘法（WLS）来进行室内定位，是一种非递归算法，其优点是计算量小［13］。

设锚节点的坐标为（xi,yi）（i为锚节点的序数），未知节点位置坐标为（x，y），则锚节点与未知节点之间的距离可表示为

将式（1）等号两边平方整理得到：

根据上式，有

将上述方程式展开得到：

令i=1，则ri,1=0，可以化简为

式（4）减去式（5）得到：

由式（7）可以得到误差矢量为

其中：

其中，Q代表TDOA 的协方差矩阵，Q=E[nn] ，利用最小二乘法求得（8）的解为

其中：

如果未知节点与基站距离较远时，假设距离R0与（i=2，3，…M）比较接近，那么B≈R0I，上式可以替换为

从上式Za中可以得到标签的坐标。当未知节点与基站距离较近时，由式（13）解出矩阵B，然后根据式（12）完成第一次WLS 计算。第二次估计将第一次估计得到的Za建立新的误差方程组，得到第二次位置估计。

Chan 算法在噪声服从高斯分布时［14］，有着良好的定位精度。Chan 算法有一定的局限性，在复杂的室内环境下由于非视距（NLOS）影响，定位精度明显有所下降。

3 Taylor级数展开法

Taylor 算法过于依赖初始估计位置，当初始估计位置与实际距离比较接近时，则Taylor 算法有比较精确的定位精度，如果初始值估计值选取不合适，则可能导致该算法不收敛。在实际的环境中，一般很难确定初始位置，所以导致其定位精度受到一定的影响［15］。

fi=(x,y,xi,yi)在(x0,y0) 处的Taylor 级数展开结果如下所示：

忽略式（14）中的次数大于二的项，得到的结果：

其中：

ri(i=1,2,3,…,L)表示锚节点和未知节点之间的距离。

式（16）的WLS解为

上式中Q表示TDOA 的测量协方差矩阵。

Taylor 算法每一次算出的结果(x0,y0)带入下一次迭代，直到||Δx+||Δy<ε时估计出待测的标签值。

Taylor 算法有着高定位精度的前提是具有准确的初始估计值，初始位置影响着其收敛性，影响其算法的性能。

4 改进的CHAN-Taylor加权算法

在复杂的室内定位环境下，基站和标签之间的超宽带信号可能会被遮挡，因此基站和标签之间可能会存在一些遮挡物导致到达时间差（TDOA）值中存在一些NLOS 误差，若将此时的测量值直接代入上述算法进行计算，则定位精度会大大受影响。为了解决NLOS 影响，所以本文通过CHAN、CHAN-Taylor 分别获得估计值，对两次估计值进行加权得出最终标签位置估计。设置一个门限值来剔除NLOS误差的影响，其流程图如图1。

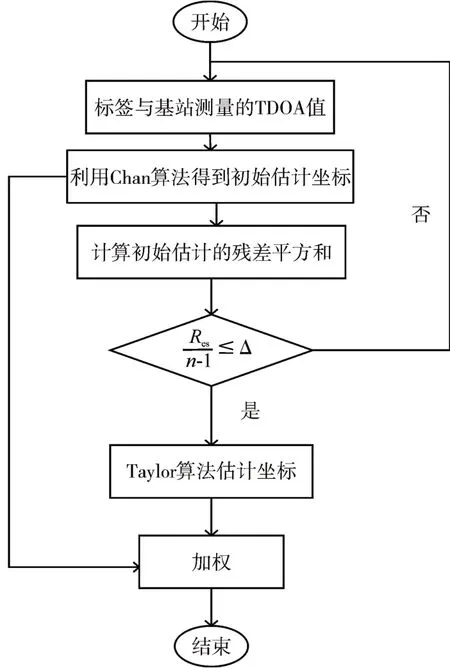
图1 算法流程图

具体计算过程如表1。

表1 算法步骤

1）计算残差平方和

将Chan 氏算法利用测得的TDOA 值进行初步估计，得出初步估计坐标（̂，̂），再计算出初始的残差平方和。

2）与门限值进行比较

在复杂的室内环境中，非视距误差是其误差的主要来源，当非视距误差影响越大，其残差计算值也就越大［12］。本文通过多次实验分析的结果设置其相应的门限值Δ，与残差进行比较，剔除在非视距环境下误差较大的TDOA值。

门限值设置合理，不能过大，要是设置过大，则不能有效剔除测量数据的异常值，若设置过小，则可能会剔除有效的测量数据，会影响定位精度。

3）进行加权处理

将筛选出来的值作为Taylor 算法的初始估计值。本文将Chan 估计值和CHAN-Taylor 级联算法估计值进行加权得到更精确的定位坐标，根据加权系数对二者进行加权处理。

KL表示第L种加权系数，RK表示定位结果和基站计算得到的距离，Rk表示标签和基站计算得到的距离。

最终定位结果：

5 实验与结果分析

在Matlab 上分别对Chan 算法，CHAN-Taylor级联算法和本文提出的改进加权算法进行仿真。分别从两个角度来进行验证：一个是通过不同基站的数目来验证，另一个就是在不同信号标准差来验证三种算法的定位精度。本文假设服从理想的高斯分布，在基站数目为4 个，5 个，信号标准差为0.4和0.6 下分别来验证。纵坐标为累计分布函数（CDF），横坐标为定位误差。

如图2~3为4个基站和5个基站下的对比实验图。

图2 4个基站

图3 5个基站

由上面实验结果分析随着标准差的增大定位精度减小，从上面仿真图来看，在相同的信道环境下，本文提出的定位精度高于另外两种定位算法。

图4~5是在信号标准差分别为0.2、0.4 下进行仿真。

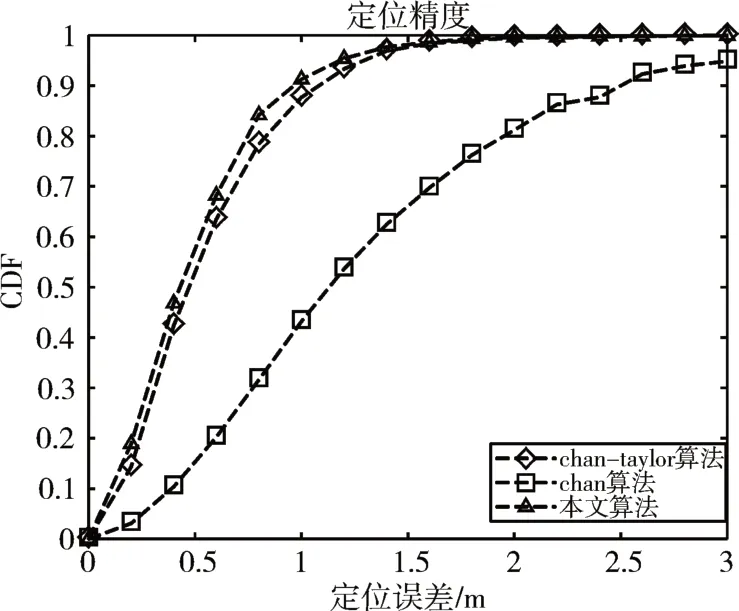
图4 标准差为0.2

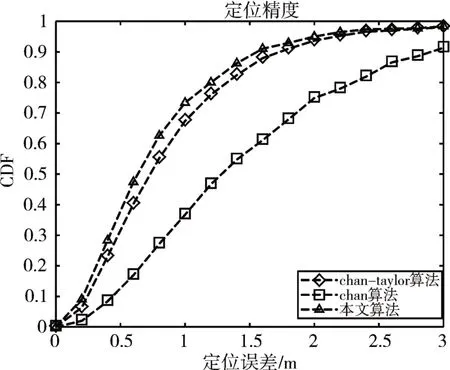
图5 标准差为0.4

在不同信号的标准差下，三种算法定位精度都是随着标准差增大而下降，在相同的信道环境下测量，由仿真结果可以表明本文改进的定位算法在不同的标准差下其定位精度最佳。

6 结语

在现实的复杂室内环境中，由于Chan 算法和Taylor 算法都存在一定的局限性。当误差服从正态分布时，在高斯信道中，通过在不同的基站数目和在不同信号标准差在Matlab 平台下进行仿真，本文提出的Chan，CHAN-Taylor 级联加权算法在定位精度上比CHAN-Taylor 加权算法提升了7.5%，并且具有良好的鲁棒性。