基于multisine 激励与整周期采样的多频电阻抗成像系统设计*

杨宇祥 白世展 林海军 李建闽 张甫

(湖南师范大学工程与设计学院,长沙 410081)

本文从周期信号的整周期采样无频谱泄露这一原理出发,提出基于multisine 信号的整周期采样理论,从理论上推导出满足multisine 整周期采样的采样率设置条件,构建了基于FPGA+数模转换器+模数转换器的整周期采样实现方法,研制了一种基于multisine 激励和整周期采样的新型多频电阻抗成像(mfEIT)系统;设计了胡萝卜棒+黄瓜棒的双目标成像模型,并进行了多频时差成像和频差成像实验.实验表明,本mfEIT 系统能够在一个基波周期(1 ms)内实现20 个频率点(2—997 kHz)多目标组织边界的全频阻抗测量,成像结果可区分具有不同电特性生物组织的结构与位置.本文提出的基于multisine 信号的整周期采样理论及其实现方法,只需一个multisine 基波周期即可完成一次全频阻抗测量,为研制高速mfEIT 系统奠定了理论和技术基础.

1 引言

电阻抗成像(electrical impedance tomography,EIT)是一种通过生物组织边界电阻抗重建其内部电导率分布的可视化图像方法[1].相比于其他成熟的、非侵入性成像技术,如磁共振成像(MRI)[2]和X 射线计算机断层扫描(CT)[3],EIT 具有无辐射、低成本、小型化等优势,尤其适合连续和实时监测场合,在乳腺癌筛查[4]、肺部急性损伤检测[5]、脑部快速电活动检测[6]及体外血栓检测成像[7]等医学临床检测中得到了日益广泛的应用.传统的EIT系统通常基于单频阻抗测量和时差成像算法(timedifference EIT,td-EIT)[8],单频EIT 的一个基本问题是生物组织的绝对阻抗很难确定,只能观测生理或病理过程引起的相对阻抗变化[9];td-EIT 可反映心肺引起的体内阻抗的前后变化,但在急性卒中治疗等特殊的临床应用场合,往往因缺乏中风前的参照阻抗而使得td-EIT 成像结果无法区分缺血性卒中和出血性卒中,从而耽误治疗[10].

随着生物电阻抗谱(bioimpedance spectroscopy,BIS)测量技术的进步,基于频率依赖特性的生物组织表征已经成为可能[11],多频电阻抗成像(multi-frequency EIT,mfEIT)技术和频差成像算法(frequency-difference EIT,fd-EIT)应运而生[12].mfEIT 是EIT 与BIS 结合的技术,根据阻抗随频率的变化特性来成像,可满足不同生物组织对测量敏感频率的要求,并实现对生物组织电学特性的精确表征和二维/三维图像的实时重建[13].与td-EIT算法相比,fd-EIT 算法利用同一时间内测量得到的多频阻抗进行图像重构,不需要过去的参照阻抗,解决了实际临床环境中参考量不可获得的问题[14].此外,新的td-EIT 算法也将多频阻抗信息融合到时差成像中,降低了逆问题的自由度和病态性,可获得增强的重构图像[15].因此,mfEIT 成为EIT 研究的一个重要转变,世界各地的研究小组已经在开发mfEIT 系统方面做了大量的努力[16].

mfEIT 技术的基础是对生物体多频阻抗的快速准确测量,其测量方法主要分为扫频测量法和多频同步测量法[8].扫频测量法利用分时单频正弦激励信号步进扫描获取不同频率下的生物电阻抗信息[17].扫频测量法实现简单,目前仍是线性时不变(LTI)假设条件下测量静态阻抗的主要方法,但完成一次扫频测量的时间相对较长;而对于生命体连续变化的时变系统(如心血管系统),扫频测量法很难准确获取这种非平稳条件下的动态阻抗,从而丢失重要的诊断信息[18].多频同步测量法利用宽频激励信号一次获取多个频率点的生物电阻抗信息,测量速度是扫频测量法的2.76 倍[19],可准确记录生命时变系统某时刻的瞬时阻抗谱信息,因此多频同步测量法是mfEIT 的发展趋势[20].

多频同步激励信号的选择是实现mfEIT 系统中多频阻抗快速测量的关键,需同时满足LTI 系统的线性前提假设和活体组织的安全标准[21].本文作者前期研究证明,具有稀疏频谱分布的宽带信号(信号能量较均匀地分布在频率间隔较大的有限个频点上)是多频同步激励信号的理想选择[22].Chirp 信号(线性调频脉冲)是当前mfEIT 系统经常采用的一类多频同步激励信号,Kusche 等[23]开发的宽频EIT 系统和天津大学谭超团队[24]研发的敏感带宽SWEIT 系统均采用Chirp 作为多频阻抗测量的激励信号.Chirp 信号的优点是具有平坦宽泛的频谱范围,使用者可彼此独立地选择激励脉冲的频率范围和持续时间;缺点是频谱过于密集且存在多余的高次谐波,每条谱线上的激发能量往往太低,对测量的信噪比(SNR)影响较大[25].

最新研究证明,多频正弦(multisine)信号没有多余的高次谐波,因此具有更高的能效,对信号放大器件的压摆率要求较低(约0.3 V/μs)[19].西班牙学者Sanchez 等[26]早前已证明,相比于Chirp激励信号,采用multisine 激励信号的生物电阻抗测量系统具有高出20—30 dB 的SNR.近年来,国内外多个EIT 团队陆续开发了基于multisine 激励的mfEIT 系统,如RWTH Aachen 大学Aguiar等[8]通过9 个不同频率正弦波叠加生成多正弦同步信号,爱丁堡大学Yunjie 和Jiabin[13]通过数字配置正弦波频率与相位实现两个频率离散波形叠加,天津大学Yan 等[27]使用5 个单频正弦求和而合成多谐波波形.然而,上述mfEIT 系统的multisine激励信号均通过多个直接数字合成器(direct digital synthesizer,DDS)产生不同的单频正弦波再经累加器叠加而成,这样合成的multisine 信号所能包含的频率点个数严格受到系统DDS 硬件资源的限制,同时因参与叠加的多个正弦波相位未经优化而可能使得合成的multisine 信号具有过高的波峰因数(crest factor,CF),从而对LTI 系统的线性假设和活体组织的安全标准造成威胁[19].

本文作者早前提出基于相位迭代优化的multisine 合成算法[28],该算法可合成具有业界最小CF 值的multisine 信号.在此基础上,本文从周期信号的整周期采样无频谱泄露这一原理出发,提出基于multisine 信号的整周期采样理论,构建基于现场可编程门阵列(FPGA)+数模转换器(DAC)+模数转换器(ADC)的整周期采样实现方法,研制了一种基于multisine 激励和整周期采样技术的新型mfEIT 系统,该系统只需一个multisine 信号基波周期的整周期采样即可完成一次全频阻抗测量,可大幅提升mfEIT 的成像速度.论文设计了胡萝卜棒与黄瓜棒的多目标阻抗测量、时差与频差成像实验,以验证该mfEIT 系统的有效性.

2 Multisine 整周期采样理论与多频阻抗快速测量原理

2.1 Multisine 整周期采样理论

设时域multisine 信号x(t)包含M个谐波分量,可表示为

式中Am,fm,φm分别表示multisine 信号第m次谐波的幅值、模拟频率和初相位,m为正整数.用采样率fs对x(t)进行采样,得到离散的multisine信号x(n):

式中N为采样点数.对信号x(n)进行N点离散傅里叶变换(DFT)变换得

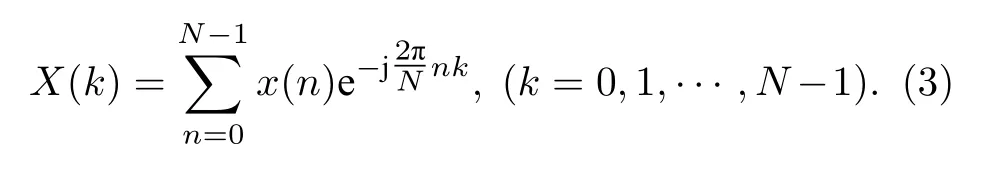
将(2)式代入(3)式,并利用欧拉公式ejθ=cosθ+j sinθ得

定义基波频率f0、采样率fs和采样点数N满足关系式

由于multisine 各频率分量满足谐波分布,即

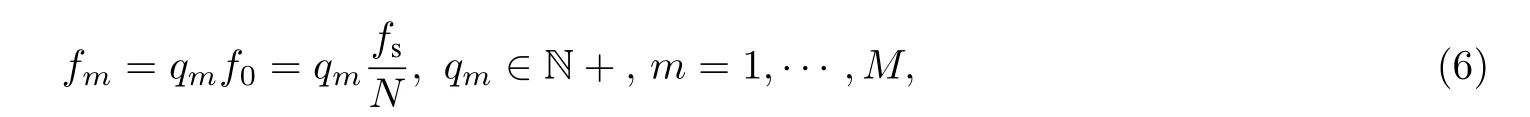
式中,qm为正整数,表示multisine 信号所包含的各次谐波分量相对于基波频率f0的倍数.将(6)式代入(4)式得

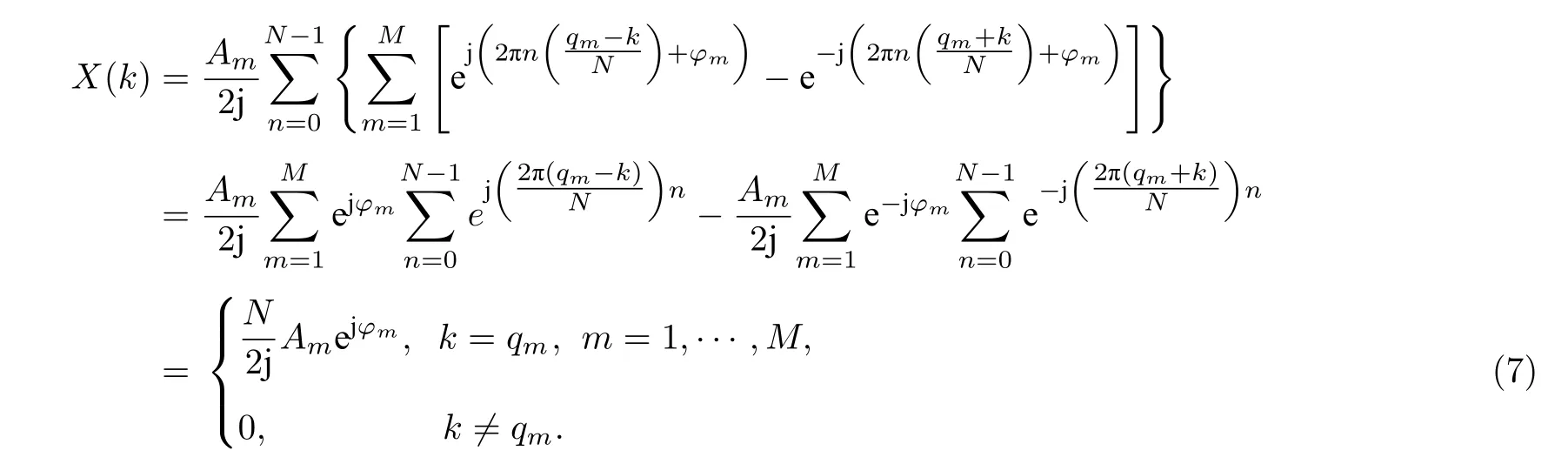
由(7)式可知,当采样点数N满足关系式(5)时,multisine 信号的频谱X(k)只在谱线k=qm(m=1,···,M)处才有非零值,频率分辨率 Δf=f0,即DFT 运算后只在qmf0(m=1,···,M) 处具有非零谱线,频谱无泄漏.一般地,若采样率fs满足:

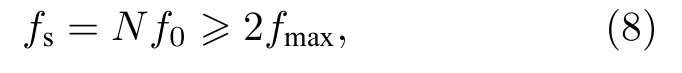
式中fmax表示multisine 信号中的最大谐波频率,则只需一个基波周期T0=1/f0即可获得N点的整周期采样,(8)式就是整周期采样的条件.为了方便快速傅里叶变换(FFT)运算,N一般取1024,2048 等2 的指数倍数值.

2.2 基于multisine 整周期采样的多频阻抗快速测量原理

基于整周期采样的多频阻抗快速测量原理如图1 所示.

图1 中,FPGA 将存储在其内部ROM 中的一个基波周期的N点离散multisine 信号顺序循环读出,经数模转换器(DAC)后转换成连续的multisine 信号,并经恒流源驱动后变为电流信号i,注入到被测阻抗ZX中,得到响应电压信号v.对i和v进行N点整周期采样,分别得到i(n)和v(n).根据信号与系统理论,对系统输入信号i(n)和输出信号v(n)进行傅里叶变换,即可得系统的频率响应H(ω):

图1 基于multisine 整周期采样的多频阻抗测量原理图Fig.1.Schematic diagram of multi-frequency impedance measurement based on integer-period sampling.

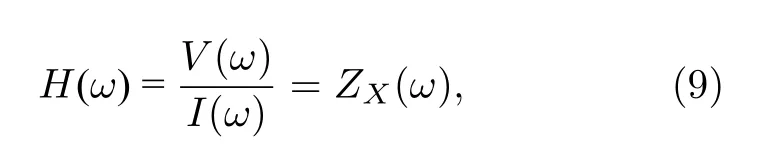
式中,I(ω)表示电流激励i的傅里叶变换,V(ω)表示电压响应v的傅里叶变换,因此,频率响应H(ω)的物理意义就是被测阻抗的阻抗谱ZX(ω).

图1 中,为了实现整周期采样,激励电流i的生成和信号的采样均受FPGA 发出的整周期采样同步时钟信号CLK 统一控制,采样率fs被精确控制为基波频率f0的N倍,因此在一个基波周期内采样后得到的离散激励电流信号i(n)和响应电压信号v(n)都包含N个点,这时在频域对i(n)和v(n)进行N点DFT 运算时,就不会引起频谱泄漏.令Ik,Φk(k=0,1,···,N— 1)分别代表激励电流i(n)进行N点DFT 运算后的幅值谱和相位谱,Vk,Ψk(k=0,1,···,N—1)分别代表响应电压v(n)N点DFT 运算后的幅值谱和相位谱.由(7)式可知,基于整周期采样的DFT 运算只在qmf0(m=1,···,M)处具有非零谱线,则被测阻抗ZX落在multisine激励信号(1)式所包含的M个谐波频率点上的多频阻抗可由下式计算得到:

式中,Zk,θk分别表示被测阻抗ZX的幅值和相位.

3 多频电阻抗成像(mfEIT)系统设计

3.1 基于FPGA 的mfEIT 硬件系统设计

本文构建了基于FPGA 的mfEIT 系统,其硬件结构原理如图2 所示.系统主要包括现场可编程门阵列(FPGA)模块、DAC 与ADC 模块以及模拟前端与电极阵列(含恒流源、差分放大电路、电极切换电路等).

图2 基于FPGA 的mfEIT 系统结构原理图Fig.2.System structure diagram of the mfEIT system based on FPGA.

图2 中,一个基波周期的multisine 信号被离散化成4096 个点预先存储在FPGA 的ROM 中,DAC 在锁相环(PLL)的控制下顺序读取ROM 中的波形值生成模拟multisine 信号,经低通滤波器(LPF)滤波后送入恒流源转变为multisine 电流信号i,通过模拟开关选择一对相邻电极作为电流激励电极,将i注入到被测生物边界阻抗ZX中,并通过参考串联电阻Rf返回恒流源;同时,通过模拟开关选择除电流激励电极以外的一对电极作为电压采集电极,测量经差分放大后得到的响应电压信号v,并同步测量Rf上的压降经差分放大后得到的电流信号i;PLL 同步控制两路ADC 分别对i和v进行同步整周期采样,分别得到离散序列i(n)和v(n)并缓存在FPGA 片内资源配置的两路先入先出(FIFO)队列中;在FPGA 上开辟FFT 运算单元,分别对i(n)和v(n)进行4096 点FFT运算,分别得到对应的傅里叶系数(即激励信号的幅值谱Ik、相位谱φk,响应信号的幅值谱Vk、相位谱Ψk),并根据(10)式计算得到本次电极配置下生物边界阻抗ZX的幅值谱与相位谱信息,即完成一次全频阻抗测量;依次切换电压采集电极,对于一个N电极的EIT 系统来说,一种激励模式下共需进行(N— 3)次全频阻抗测量.随后,切换激励电极,重复上述电压采集过程;N个电极可切换产生N种激励模式,共需进行 (N— 3) ×N个测量通道的全频阻抗测量.在获得各种电极配置下的待测场边界阻抗谱数据后,最终根据成像算法计算待测场内部各单元电导率分布,并重构测量对象时差与频差图像.

mfEIT 系统实物如图3 所示,其中FPGA 平台选用火龙果(Red Pitaya)125-14Starter Kit FPGA开发套件,该套件搭载了Xilinx 公司FPGA Zynq-7010,并集成了14 位125Msps 的双路同步ADC及DAC;设计了一个包含16 电极的圆柱体形水槽作为成像模型,该成像模型通过电极阵列切换共可构成 (16 — 3) × 16=208 种基于4 电极法的阻抗测量通道配置,FPGA 平台控制电极阵列依次完成208 个测量通道在各个频率下的边界阻抗,进而对水槽进行网格剖析,计算各单元电导率的变化并重构图像.

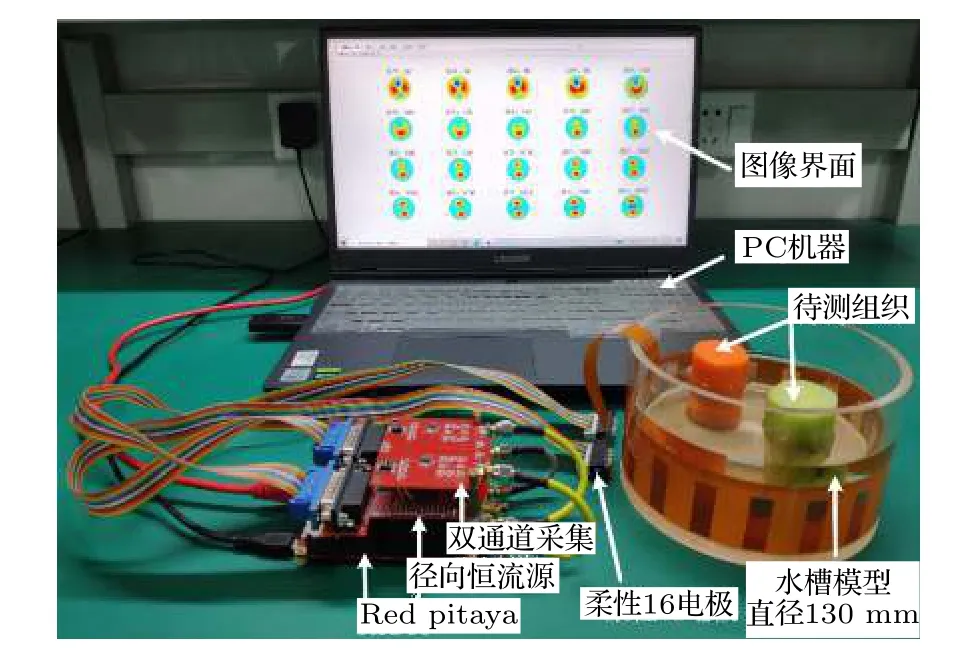
图3 mfEIT 系统实物图Fig.3.Photo of the mfEIT system.

3.2 Multisine 信号的合成

如(1)式所示,multisine 是一种通过有限个具有不同幅值、频率、相位的正弦波叠加合成的周期信号,若各正弦波分量的相位随机设置,则合成的multisine 信号往往具有较高的波峰因数(CF,峰值/有效值),这对于要求尽量压低激励信号峰值从而使被测体保持线性的生物电阻抗测量很不利.在峰值一定的情况下,拥有较高CF 的激励信号意味着较低的能量注入被测体;反之,激励信号拥有较低的CF 意味着可以提供更多的能量从而提高测量精度[29].因此,为了使multisine 激励信号在测量生物电阻抗时拥有最大的测量精度,通过合适的相位组合优化以最小化其CF 值是必然选择.关于multisine 的相位优化算法,国内外学者已经研究很多年,先后发展出解析法[30]和迭代法[31]两大类别,但各有其优缺点.

本文作者综合解析法和迭代法的优点,提出一种改进相位迭代优化的multisine 合成算法[28],该算法可以按用户所需合成任意频谱分布的multisine信号,并具有业界最小的CF 值,可显著提高阻抗测量系统的精度.本文利用此算法合成了一种包含20 个等幅值质数伪对数频谱分布的multisine信号,其各个谐波分量对应的频率、初相位如表1所列,其中各个频率分量的归一化幅值均为0.3162,基波周期f0=1 kHz.multisine 信号一个完整周期的时域波形和频谱分布分别如图4(a)和图4(b)所示.此multisine 信号通过伪对数频谱分布保证宽频测量范围,而质数频点则保证各频点之间无谐波关系,从而减小非线性谐波畸变对阻抗谱测量的影响.

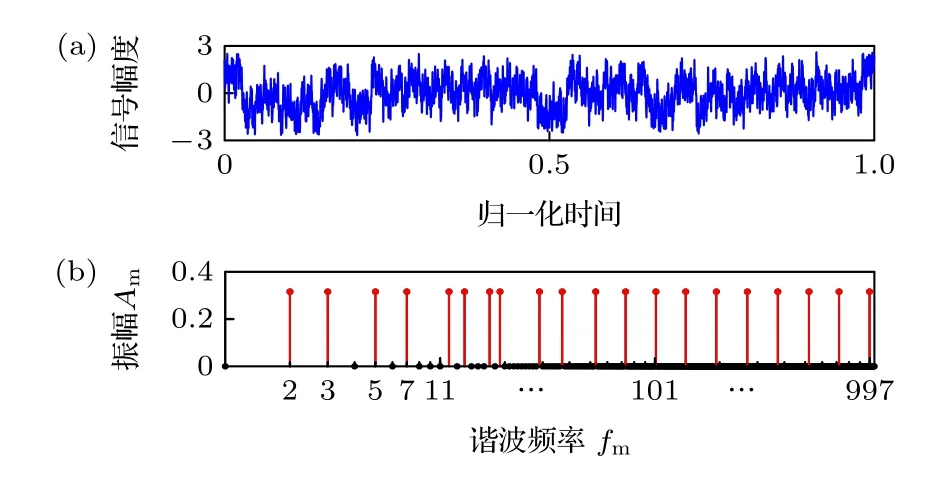
图4 Multisine 信号 (a)时域波形;(b)频谱分布Fig.4.Multisine signal:(a) Time domain waveform;(b) spectrum distribution.

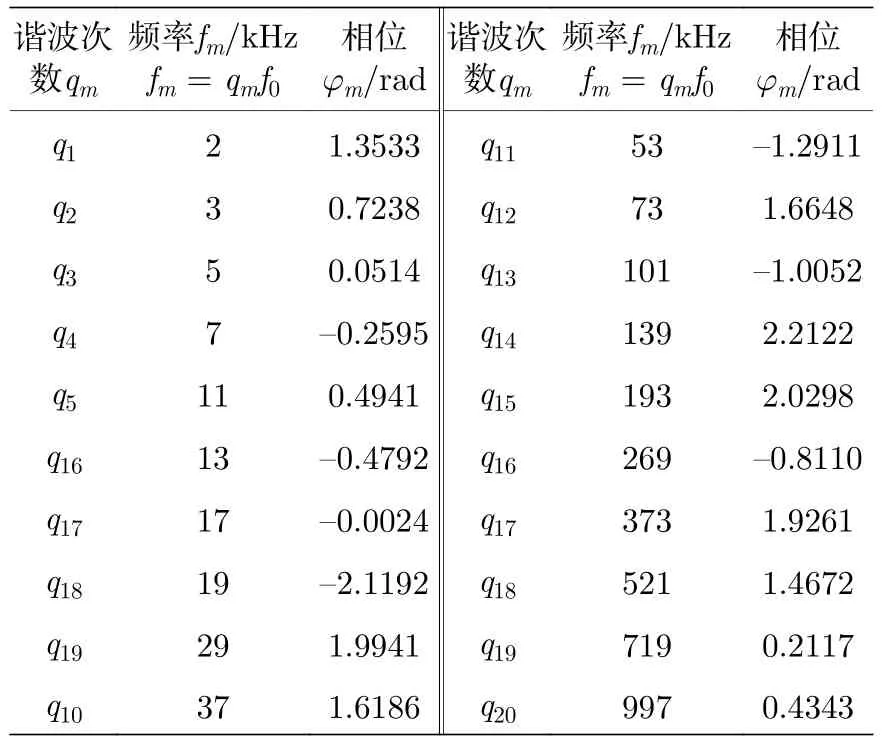
表1 合成的包含20 个等幅值伪对数频谱分布的multisine 信号频率、相位Table 1.Frequencies and phases of the synthesized multisine signal with equivalent amplitude and pseudo-logarithmic spectral distribution.

3.3 系统信噪比分析

基于本文合成的multisine 激励,对所研制的mfEIT 系统在不同频率下进行了信噪比(SNR)评估.测量选用上述水槽均质场模型,采用电导率为0.07 S/m 的盐水作为传感对象.采用相邻电极法,对生成一帧图像所需的208 个通道进行阻抗谱测量,通过下式评估各频率点的SNR:

式中,Zk为通道在频率fk时对应的阻抗测量平均幅值;为频率fk时对应的阻抗测量模值方差,分别定义为

式中,P为测量次数,每个通道进行50 次阻抗谱重复测量;分别对应于输入电流激励和输出电压响应在频率fk时对应的测量信号幅值平均值与方差.

各频率点SNR 的估计值如表2 所列,结果表明,各频率点的SNR 较为均衡,平均SNR 为55.3 dB,平均标准差为 ± 6.2 dB.由于盐水的电导率随测量频率理论上近似不变,因此高频与低频段的SNR 相差不大,而2 kHz 有明显变小的主要原因可能是低频电极接触阻抗影响较大,导致测量阻抗的准确性下降.

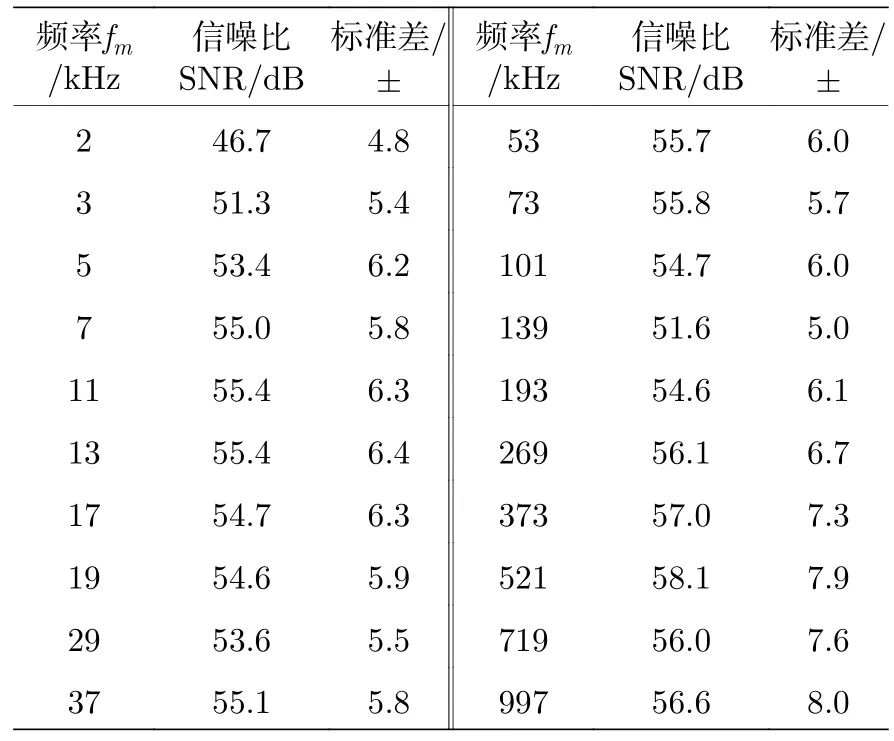
表2 Multisine 信号20 个频率点的通道信噪比平均值及标准差Table 2.Average and standard deviation of the channel SNR at 20 frequency points of the multisine signal.

4 mfEIT 成像实验与验证

4.1 mfEIT 成像方法

待测场生物组织可视为离子导电体,内部单元电导率σ(x,y)和可测参数边界电极间电位φ的函数关系为

式中∂Ω为场域边界,n表示场域Ω的外法向单位向量,j表示流入场域Ω的激励电流密度.

为了计算边界阻抗ΔZ与场域Ω内部各单元Δσ(x,y)分布之间的关系,利用联合仿真软件(COMSOL Multiphysics 5.3a with MATLAB)仿真正演模型.为更接近于真实实验效果,构建实验水槽二维仿真模型(直径130 mm),16 个弧形电极传感器宽度与相互之间间隔呈1∶1.5 比例均匀围绕模型一圈,同时设置仿真模型内溶液电导率(液体的电导率参数设置为0.01 S/m).在研究稳态物理电流场中利用有限元网格剖分分析模型场域内电位分布情况,计算得到场域内各节点电位与电导率之间关系,用灵敏度矩阵J近似表示为

1)时差成像:待测场生物组织阻抗Zf可用mfEIT 系统测量得到:

式中fm表示第m个谐波频率分量.当边界电压产生波动时,时差成像中用起始时刻t0从均质场获取边界阻抗信息作为参考数据,ti时刻同一频率阻抗变化ΔZf(t)用于时差图像重建,ΔZf(t)计算公式为

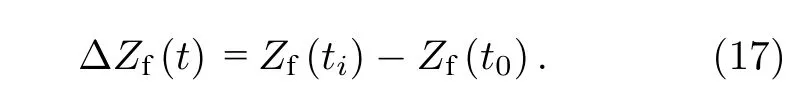
2)频差成像:与时差成像方法相比,频差成像不需要过去时刻的阻抗参考值,可解决临床环境中无法获取参考时刻边界阻抗的问题.以任意时刻ti的不同频率下阻抗数据变化ΔZt(f)进行图像重建,ΔZt(f)计算公式为

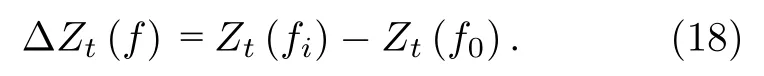
3)图像重建:利用边界阻抗变化ΔZ[ΔZf(t),ΔZt(f)]计算内部各单元电导率变化Δσ(x,y),重构出目标组织结构.利用Tikhonov-Noser 组合正则化算法优化计算目标场内部各单元电导率的变化:

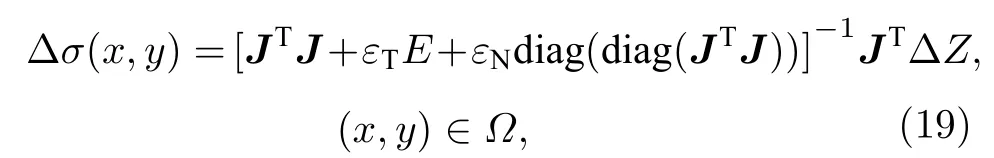
式中,εT是Tikhonov 正则化参数,εN是Noser 正则化参数,E是与JTJ维度相同的单位矩阵.

EIT 逆问题的求解是一个非线性病态问题,解存在严重的不稳定性.本文选择Tiknonov-Noser组合正则化算法作为图像重构的算法,目标为改善其非线性的病态问题,变成最小化目标函数的求解,这样可以得到存在且唯一的稳定解.选用Tiknonov-Noser 正则化算法对EIT 逆问题的求解,既可以提供正确的成像目标位置又可以很好地去除噪声干扰[32,33].正则化参数是一个需要人为设置的经验常数,对重构图像的质量至关重要,经实验验证正则化参数εT=1×10-6,εN=100 是比较合适的值.

4)图像质量评价:为了定量评估重建图像的准确性,采用归一化的实验模型电导率变化与仿真模型电导率变化之间的相关系数(CC)作为图像质量的评价指标,定义如下:

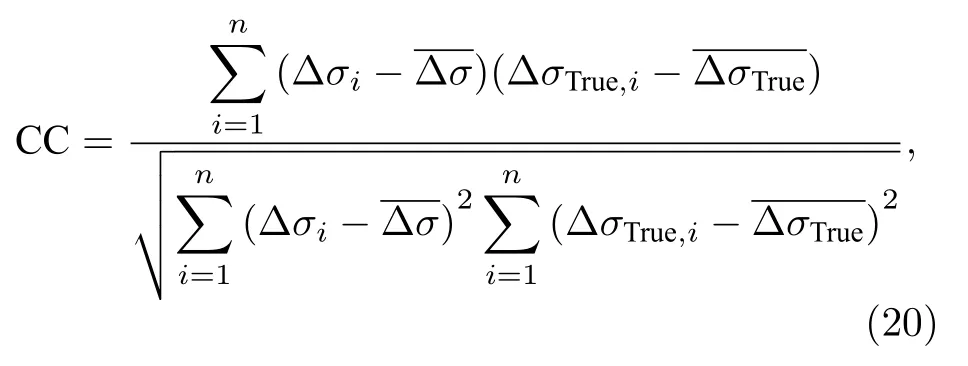
式中,Δσi,ΔσTrue分别表示第i个元素的重建电导率和仿真电导率的变化值,分别表示重建电导率和仿真电导率的变化平均值,n为根据COMSOL 有限元剖分方法得到的网格节点数,本文中n=3360.

CC 与电导率的具体值无关,仅与电导率的空间分布有关.因被测目标的电导率随频率变化,在不同基础参考频率下选择不同频率间隔可以获得不同的图像,频差成像的质量难以评价[34],故本文仅对时差图像进行质量评价.

4.2 mfEIT 系统成像实验

4.2.1 时差成像

在成像实验开始前,先测量圆柱体形水槽内只有盐水时的均质场边界阻抗谱数据,作为时差成像中的参考数据Zf(t0).均质场边界阻抗谱如图5 所示.由图5 可见,不同频率下的均质场边界阻抗谱变化规律基本一致,只是随着频率增加,溶液的边界阻抗谱降低,边界阻抗从低频(2 kHz)时的150 Ω降至高频(997 kHz)时的不足50 Ω.

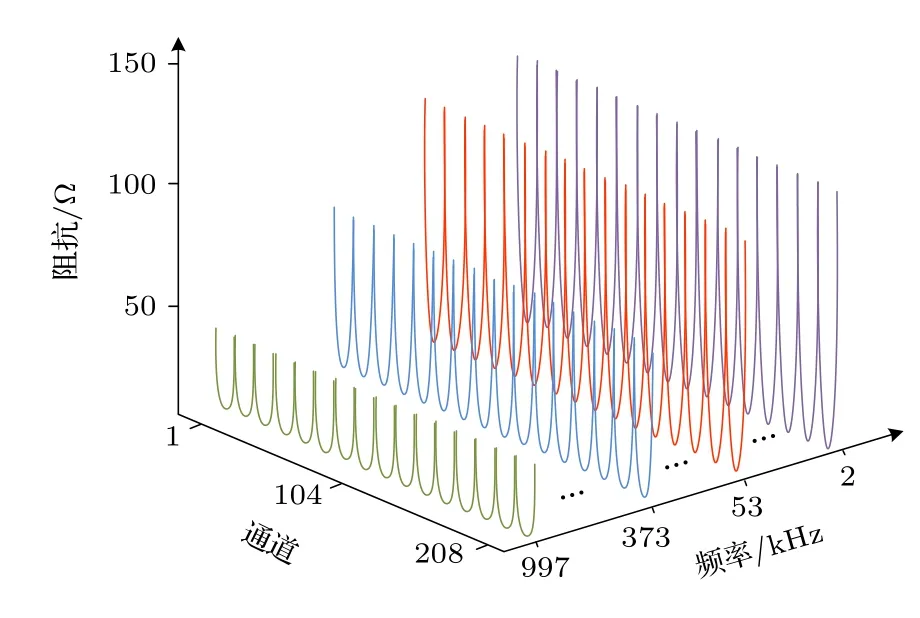
图5 均质场边界阻抗谱Fig.5.Boundary impedance spectroscopy of homogeneous field.

在测得均质场边界阻抗谱数据基础上,将胡萝卜棒和黄瓜棒放入水槽(如图3 所示),利用(17)式和(19)式得到多频阻抗时差图像,图6 中依次显示了胡萝卜棒和黄瓜棒在20 个频率激励下(2—997 kHz)的时差图像,图像下方的小数值分别代表各个频率下图像重建结果与仿真模型相关度(即(20)式表示的图像评价指标CC),CC 越接近于1 则表示成像结果相关度越高,成像质量越好.图6 中,图像质量最好的频率范围是73—373 kHz(CC ＞ 0.700).由图6 可见,胡萝卜棒和黄瓜棒的电导率变化值由低于溶液电导率的变化逐渐升高,成像颜色由蓝色渐变到红色的变化.其中胡萝卜棒在13—53 kHz,黄瓜棒在513 kHz,电导率变化与溶液电导率变化相近,故其在此频率下目标图像并不明显甚至“消失”.而在低频和高频区,由于萝卜棒和黄瓜棒与溶液电导率差值的影响,靠近边界的灵敏度高于中心区域灵敏度,重构图像的两个目标之间产生了阴影.

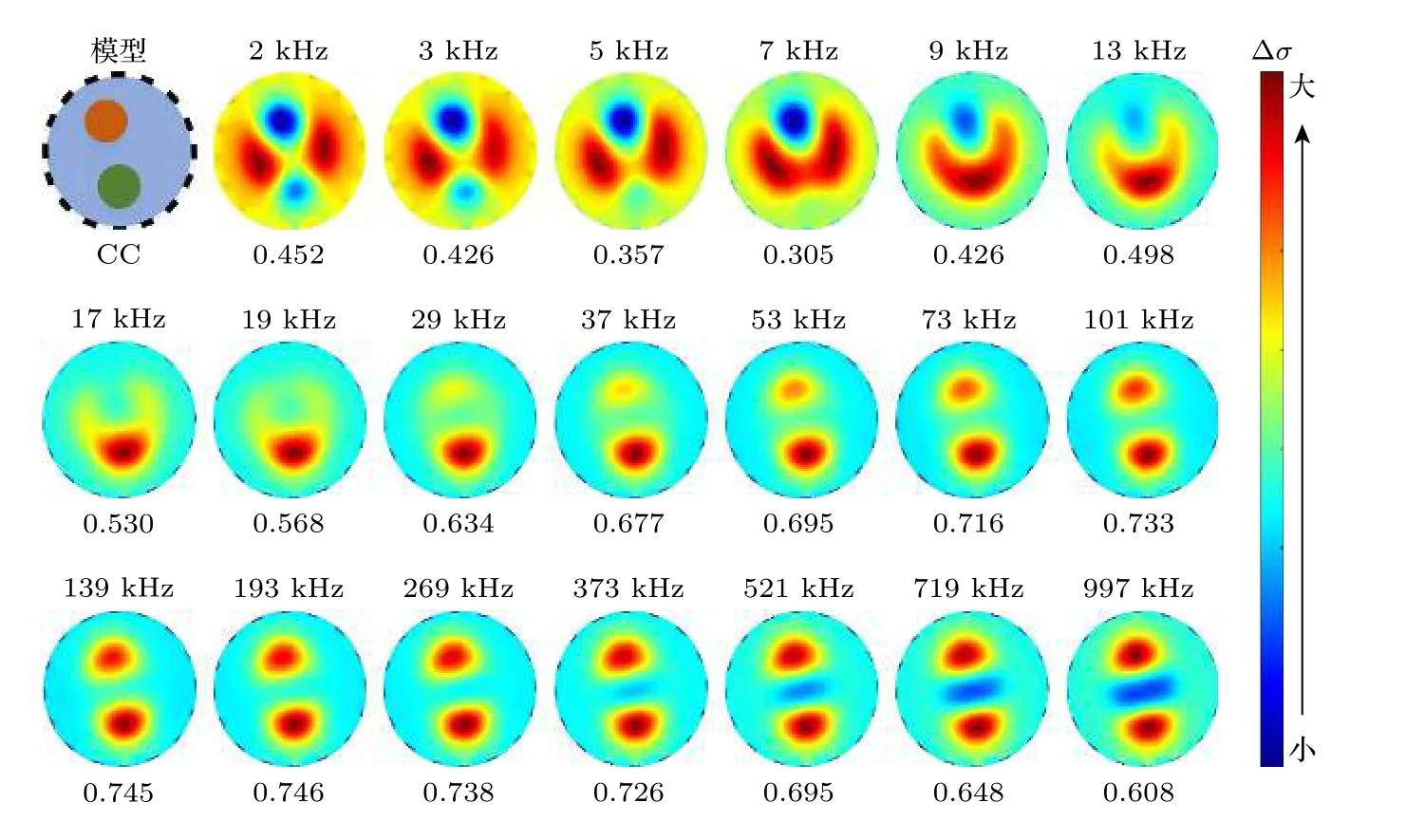
图6 mfEIT 系统的时差成像Fig.6.Time difference images of the mfEIT system.

4.2.2 频差成像

频差成像选择同时刻2 kHz 激励下的边界阻抗数据作为基础参考数据,利用(18)式和(19)式得到同时刻的多频频差阻抗图像,图7 是胡萝卜棒和黄瓜棒在multisine 激励(2 —997 kHz)下的多目标阻抗频差图像.图7 中,在激励频率小于269 kHz 时,胡萝卜棒和黄瓜棒的电导率变化明显均高于溶液,且黄瓜棒的电导率变化高于胡萝卜棒,因此二者的成像颜色不同.

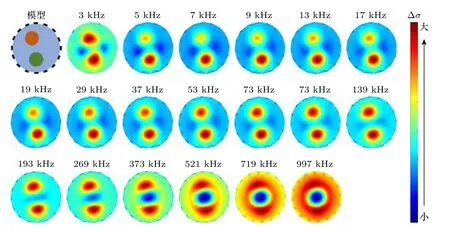
图7 mfEIT 系统的频差成像Fig.7.Frequency difference images of the mfEIT system.

从上述时差和频差成像实验的结果来看,本文所设计的mfEIT 系统能够对多目标生物组织进行检测与成像,并可通过对目标阻抗谱与多频图像重建结果进行分析,以识别和区分不同的生物组织,突出不同目标生物组织在宽频率范围下的阻抗变化特点和成像变化趋势.

5 结论

本文从周期信号的整周期采样无频谱泄露这一原理出发,提出基于multisine 信号的整周期采样理论,首次从理论上推导出满足multisine 整周期采样的采样率设置条件;构建了基于FPGA+DAC+ADC 的整周期采样实现方法,研制了一种基于multisine 激励和整周期采样的新型mfEIT系统;设计了胡萝卜棒+黄瓜棒的双目标成像模型,并进行了多频时差成像和频差成像实验,实验表明,本mfEIT 系统能够在一个基波周期(1 ms)内完成一次包含20 个频率点(2—997 kHz)的全频阻抗测量,成像结果可区分具有不同导电特性生物组织的结构与位置.本文提出的基于multisine 信号的整周期采样理论及其实现方法,只需一个multisine 基波周期即可完成一次全频阻抗测量,为研制高速多频EIT 系统奠定了理论和技术基础.下一步将通过提高基波频率大幅提升单次全频阻抗的测量速度,并通过设计并行阻抗测量方式大幅缩减EIT 多通道阻抗测量的时间,实现基于FPGA 的高速mfEIT 系统,并将其应用于生命体的动态实时成像,如肺通气监测、心搏血量检测等.