基于支撑先验与深度图像先验的无预训练磁共振图像重建方法*

赵地 赵莉芝 甘永进 覃斌毅

1) (玉林师范学院,广西高校复杂系统优化与大数据处理重点实验室,玉林 537000)

2) (中央民族大学信息工程学院,北京 100081)

3) (玉林师范学院物理与电信工程学院,玉林 537000)

基于深度学习的磁共振成像(magnetic resonance imaging,MRI)方法需要大规模、高质量的病患数据样本集进行预训练.然而,由于病患隐私及设备等因素限制,获取大规模、高质量的磁共振数据集在实际临床应用中面临挑战.本文提出一种新的基于深度学习的欠采样磁共振图像重建方法,该方法无需预训练、不依赖训练数据集,而是充分利用待重建的目标MR 图像的结构先验和支撑先验,并将其引入深度图像先验(deep image prior,DIP)框架,从而削减对训练数据集的依赖,提升学习效率.基于参考图像与目标图像的相似性,采用高分辨率参考图像作为深度网络输入,将结构先验信息引入网络;将参考图像在小波域中幅值大的系数索引集作为目标图像的已知支撑集,构造正则化约束项,将网络训练转化为网络参数的最优化求解过程.实验结果表明,本文方法可由欠采样k 空间数据重建得到更精确的磁共振图像,且在保留组织特征、细节纹理方面具有明显优势.

1 引言

磁共振成像(magnetic resonance imaging,MRI)是一种非入侵性成像技术,可为临床诊断提供结构、功能及解剖信息.MR 成像时间与k空间采样数据量直接相关,高质量成像需大量k空间采样数据,导致数据采集时间长,严重制约了MRI临床吞吐量和成像质量.为加速MR 成像,可通过减少k空间采样数据量来缩短扫描时间,研究从欠采样的k空间数据实现高质量的快速磁共振成像一直是相关领域的热点及重点研究方向.

由欠采样k空间数据重建MR 图像以实现快速MRI,本质上是求解高度欠定逆问题.基于信号处理理论的一类方法发展迅速,该类方法通过引入关于目标MR 图像函数的先验信息,利用正则化方法在保证解的唯一性与稳定性的前提下完成重建.尤其随着压缩感知(compressed sensing,CS)理论[1]的提出,稀疏性成为一种广泛使用的构造先验信息的性质,包括固定稀疏变换(如小波或/和梯度)[2,3]以及更为灵活的自适应稀疏表示(如数据驱动的紧密框架[4]及字典学习[5,6]).在实际应用场景中,预先获取的高分辨率参考图像也可提供先验信息,因其与目标MR 图像之间具有结构相似性,可获得更为稀疏的差异图像[7,8].此外,可将结构化先验信息,例如支撑信息[9,10]和结构化稀疏性(如组稀疏性、块稀疏性及树稀疏性等)[11,12]引入基于联合子空间(union-of-subspaces)采样理论[13]的重建模型,有效提高重建精度.

近年来,深度学习在医学成像领域受到了广泛关注.在MR 图像分割、去噪、分类和快速成像方面[14]的成果大量涌现.基于深度学习的MRI 方法既有数据驱动(data-driven)的,也有模型驱动(model-driven)的[15,16].数据驱动方法旨在学习从欠采样k空间数据/图像到完全采样k空间数据/图像的映射[17-20].模型驱动方法从MR 图像重建模型出发,将迭代重建算法流程引入网络[21-23].然而,它们都需要借助大规模、高质量的基于病患的临床数据集进行预训练,以确保重建精确性.而由于病患隐私及设备应用限制,获取庞大数量的高分辨率MR 图像训练集具有相当难度,成为制约临床应用的一大挑战.

由Ulyanov 等[24]提出的深度图像先验(deep image prior,DIP)框架表明,卷积神经网络具有在不进行预训练的情况下正则化各种不适定逆问题的固有能力[25].DIP 将随机噪声输入未经训练的网络,在成像逆问题中获得了良好效果.DIP 已用于去噪、修复、超分辨率重建[26-29]、CS 恢复[30]以及医学成像(如PET 图像重建[25]、CT 重建[31]和动态MRI[32])等领域.

本文提出一种基于支撑先验与深度图像先验的无预训练MR 图像重建方法,该方法属于深度学习类的欠采样MR 图像重建方法.本文所提方法无需预训练、不依赖训练数据集,将目标图像的支撑先验和结构先验融入DIP 框架,利用这些先验信息提升学习效率.实验结果表明,该方法可获得更为精确的重建结果,且在保持组织边缘与细节方面更具优势.本文的创新与贡献主要体现在以下方面.

1)利用一幅已知参考图像为目标图像的重建提供支撑先验和结构信息.由于参考图像与目标图像之间的结构相似性,一方面,将参考图像作为深度神经网络的输入,以引入目标图像的结构先验至学习进程;另一方面将参考图像在小波域中大系数的索引集作为目标图像的已知支撑集,并将其补集的l1范数正则化约束项增加至传统DIP 中.支撑先验与结构先验信息的引入可显著提升学习的有效性与效率.

2)本方法是一种无需预训练、不依赖于训练数据集的深度学习类磁共振图像重建方法.本方法基于DIP 框架,将网络训练转化为网络参数的最优化求解过程.鉴于高质量MR 数据集的获取难度,此优势具有实际的临床意义与价值.

2 重建方法

图1 为本文提出的基于支撑先验与深度图像先验的无预训练磁共振图像重建方法总览图.目标MR 图像的重建可分解为3 个步骤.

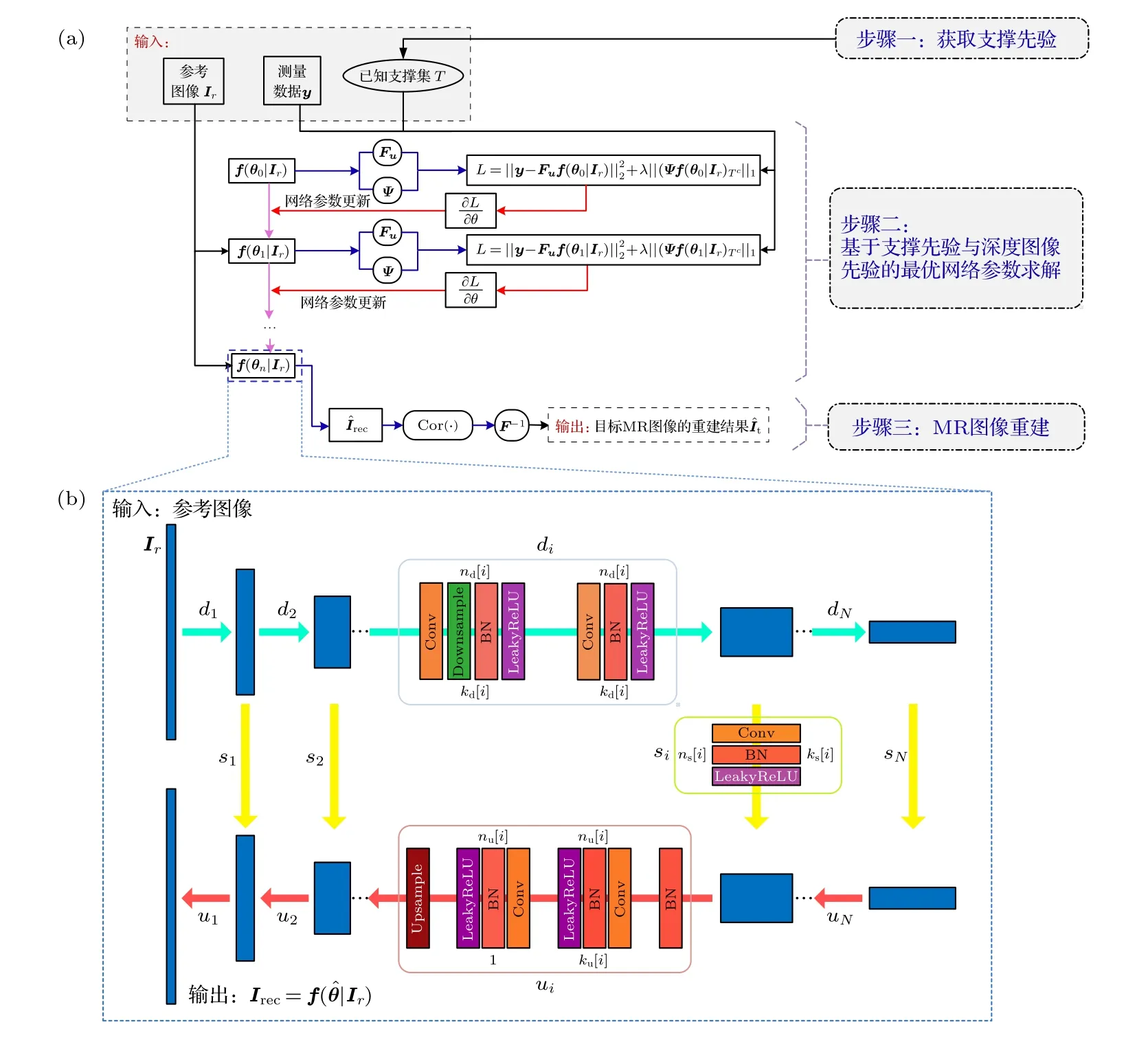
图1 方法总览图 (a)本文重建方法总体步骤;(b)本文重建方法采用的网络架构[24]Fig.1.Overview of the proposed method:(a) Overall process for the proposed reconstruction method;(b) network architecture[24]used in the proposed method.

1)获取支撑先验.本步骤基于参考图像与目标图像的结构相似性,从已知参考图像的小波域支撑中获取关于目标图像的支撑先验.

2)基于支撑先验与深度图像先验的最优网络参数求解.本步骤基于DIP 框架,提出融合支撑先验的目标函数,将对网络的训练转化为网络参数的最优化求解,无需预训练、不需训练数据集.

3) MR 图像重建.上一步求解得到的最优网络参数下的网络输出即为k空间测量数据对应的重建结果,本步骤进一步利用测量数据对重建结果进行数据矫正以提高重建精度.

下文将对该方法分步进行详细叙述.

2.1 获取支撑先验

在实际临床MRI 应用中,通常对同一病人同一组织器官进行多次连续扫描,以确保通过多幅MR 图像对病灶区域进行综合判断.由于组织器官的连续性,这些图像间,尤其是连续图像间具有非常相似的结构;此外,对于介入式手术成像、序列成像、动态MRI、连续帧之间的相似性更加显著.图2(a)和图2(b)分别为同一病人脑部不同层面的MR 成像,可以看出,它们不仅在像素空间具有相似的结构特征,而且经同一小波变换后亦具有相似的能量分布,如图2(c)和图2(d)所示.由图2可以看出,两幅结构相似的MR 图像在小波变换下,刻画组织概貌的低频系数(幅值大的系数)具有近似相同的支撑分布.因此,本文考虑选取已知参考图像在小波域中幅值最大的P个小波系数对应的索引集作为目标图像的已知支撑集T.

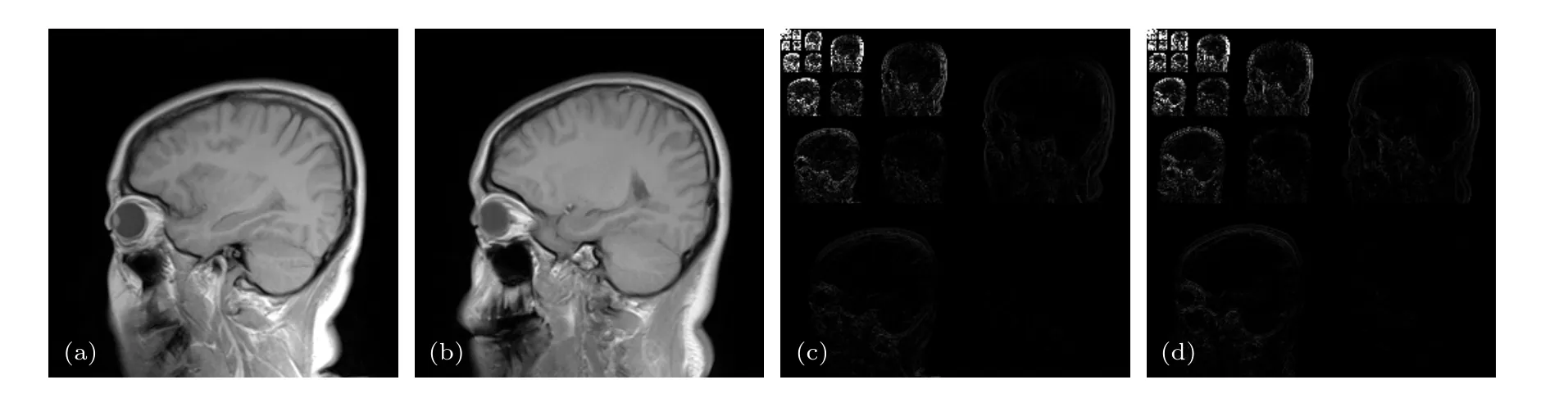
图2 参考图像和目标图像的结构相似性及小波域支撑分布 (a),(b)同一病人的脑部扫描MR 图像;(c),(d)对应的小波系数分布(Haar 小波,9 层小波分解)Fig.2.Structural similarity between the reference and target images and support distributions in the wavelet domain:(a),(b) Brain MR images from the same patient;(c),(d) corresponding wavelet coefficient distributions (Using Haar wavelet at level 9).

2.2 基于支撑先验与深度图像先验的最优网络参数求解

本方法中最优网络参数可通过求解如(1)式所示的最优化问题获得:

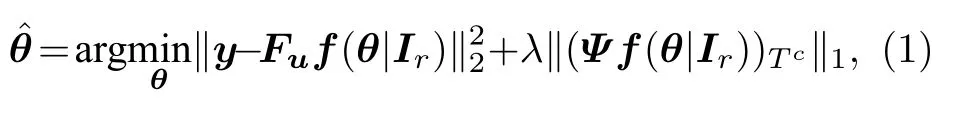
其 中,y ∈CM×1是 目 标图 像It∈CN×N的k空间测量数据;Ir ∈CN×N为提前获取的高分辨率参考图像,其与目标图像具有相似的解剖结构;Fu代表傅里叶降采样算子;Ψ代表小波变换;‖·‖2与‖·‖1分别为l2范数与l1范数;正则化参数λ ＞0 ;f(θ |Ir)是以参考图像为输入、以θ为参数的未经训练的深度神经网络;T为目标图像的已知支撑集,Tc代表已知支撑集T的补集.

本文基于DIP,提出如(1)式所示的目标函数,将深度神经网络的训练转化为网络参数的最优化求解,通过反复迭代地优化求解获得最优网络参数.第一项为数据保真项,用来约束网络输出与k空间测量数据的一致性.本方法将已知的参考图像作为网络输入,由于参考图像与目标图像的结构相似性,此策略能够充分利用并引入结构化先验至深度网络.相较于DIP 采用随机噪声作为网络输入,本方法将有利于提升学习效率.

(1)式中的第二项为正则化项,用于约束部分支撑T已知的目标图像在小波域的稀疏性,该项的引入基于Modified-CS 理论[33].该理论证明,若已知信号的部分支撑T,则可通过约束该信号在已知支撑集补集Tc上的l1范数,在相同采样数据量下获得更高精度的重建结果.由于参考图像与目标图像具有相似的解剖结构,在小波变换下,两者刻画组织概貌的低频系数具有近似相同的支撑分布.因此,考虑选取参考图像Ir在小波域中具有较大幅值的小波系数对应的索引集作为目标图像It的已知支撑集T.

2.3 MR 图像重建

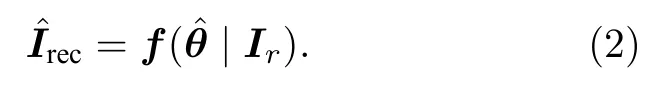
为进一步确保测量数据的一致性,增加数据矫正步骤,即对网络输出的重建图像作用数据矫正算子 Cor(·),可得经矫正的k空间数据ycor:

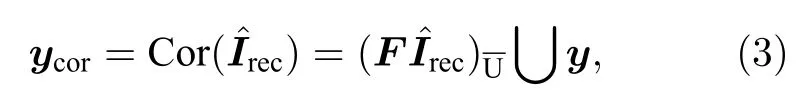
其中,F是傅里叶变换,y是欠采样模板U 下对应空间位置处的测量数据,U 代表U 的补集.(3)式所示的k空间数据矫正算子保证了重建结果与扫描获取的k空间测量数据的完全一致性,使得重建误差仅集中于未采样的k空间数据.

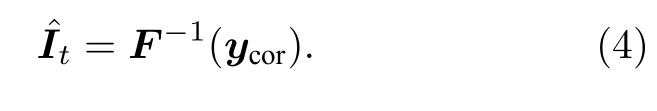
2.4 网络结构

本文方法采用U-net 网络架构,与DIP 方法[24]采用的网络架构相同.图1(b)给出了该网络架构,它是一种具有跳跃连接、形如“沙漏”的编码器-解码器架构.其中,编码路径(上)和解码路径(下)由跳跃连接(黄色箭头标记)链接,以保留不同分辨率下的特征信息.该网络包括卷积(Conv)层、批标准化(batch normalization,BN)层、泄漏校正线性单元(LeakyReLU)层、降采样(downsample)和双线性插值上采样(Upsample)的重复应用.网络的最大深度为L.nd[i],nu[i]和ns[i]分别表示第i层降采样、上采样和跳跃连接的滤波器数量,kd[i],ku[i]和ks[i]表示对应的核大小.

3 实验与分析

3.1 实验设置

3.1.1 对比方法与评价指标

实验中,将零填充重建、基于CS 的MR 图像重建及传统DIP 重建作为对比方法,以评估所提出方法的重建性能.其中,基于CS 的MR 图像重建方法采用如下的重建模型:

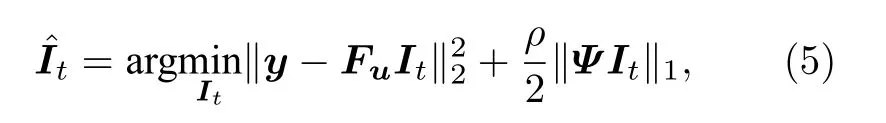
式中,Ψ为小波变换,即利用MR 图像的小波域稀疏性约束重建,下文简称该方法为CS-WS.实验中选用Daubechies 小波db2,采用迭代阈值收缩算法 (iterative shrinkage thresholding algorithm,ISTA)求解.

为确保公平对比,所有方法都使用与零填充重建相应的k空间测量数据作为输入,且本文方法和传统DIP 方法采用相同的网络架构.

采用相对误差、峰值信噪比(peak signal-tonoise ratio,PSNR)以及结构相似性(structural similarity index,SSIM)[34]作为重建结果的量化评价指标:

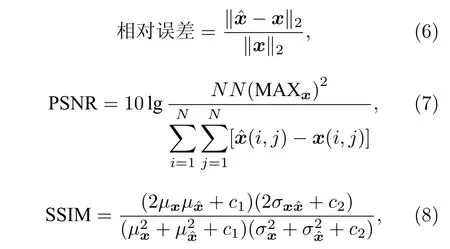
其中,x表示真实MR 图像,表示重建MR 图像,两者大小均为N ×N;MAXx取x中最大值.此外,(8)式中,μx,,σx,和分别为x和的均值与方差,σx表示x和xˆ的互协方差,常数c1=0.01,c2=0.03.

3.1.2 数据获取

为验证本文方法的有效性,并评估其重建性能,选取两组临床获取的人体脑部MR 图像进行仿真实验,如图3 所示.为模拟欠采样k空间数据的获取过程,使用降采样模板作用于MR 图像的二维(2D)离散傅里叶变换.实验所用的两组MR数据均来自3T Siemens MRI 扫描仪,第一组MR数据成像参数为:SE 序列,偏转角=120°,TR=4000 ms,TE=91 ms,FOV=176 mm×176 mm,层厚 5.0 mm.图像大小为 256×256.选取图3(a)作为参考图像,为图3(b)所示的目标图像(记为目标图像1)的重建提供结构先验和支撑信息.第二组MR 数据成像参数为:GR 序列,偏转角=70°,TR=250 ms,TE=2.5 ms,FOV=220 mm×220 mm,层厚 5.0 mm.此组MR 数据取自于同一病人的脑部扫描序列,图像大小为 512×512.此处选取图3(c)作为参考图像,分别为图3(d)和图3(e)两幅目标图像(分别记为目标图像2、目标图像3)的重建提供结构先验和已知支撑信息.

图3 实验数据.第一组 (a)参考图像;(b)待重建的目标图像1.第二组 (c)参考图像;(d)待重建的目标图像2;(e)待重建的目标图像3Fig.3.MR images used in the experiments.Group one:(a) Reference image;(b) target image 1.Group two:(c) Reference image;(d) target image 2;(e) target image 3.

考虑到不同采样模板对本文方法重建性能的影响,采用3 种类型的采样模板:笛卡尔采样模板、径向采样模板和变密度采样模板,如图4 所示.

图4 降采样模板 (a)笛卡尔采样模板;(b)径向采样模板;(c)变密度采样模板Fig.4.Undersampling masks used in the experiments:(a) Cartesian mask;(b) radial mask;(c) variable density mask.

3.1.3 实验参数设置

本文方法采用的网络架构如图1(b)所示,实验中所涉及的各参数设置均在表1 中列出.其中包括网络超参数、小波参数(小波函数及分解层数)、已知支撑集(选取参考图像的最大系数个数P.经实验验证,通常选取参考图像最大的前20%小波系数索引集作为已知支撑集)和正则化参数λ.

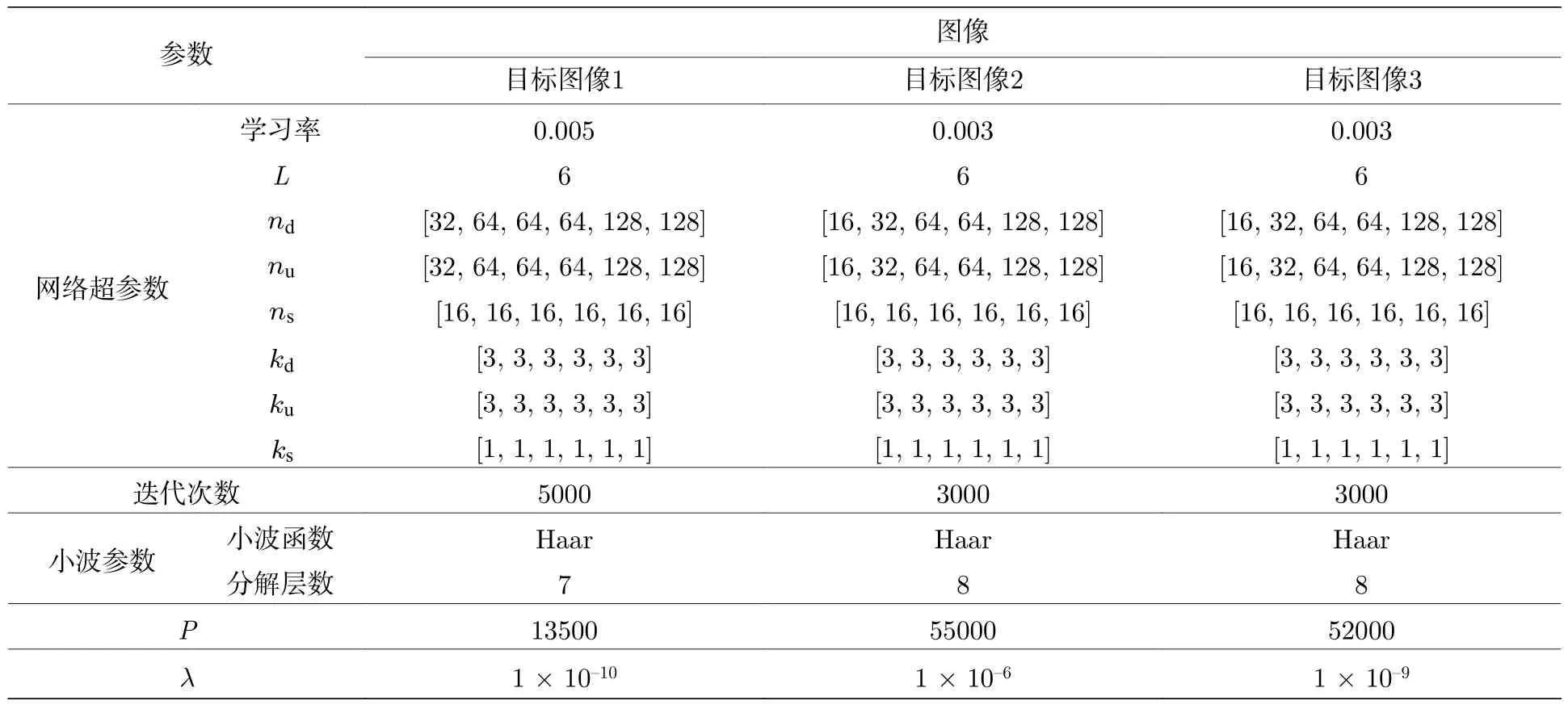
表1 实验参数设置Table 1.Parameter setting for experiments.

本文实验在Ubuntu 16.04 LTS (64 位)操作系统上实现,平台配置为Intel Core i9-7920X 2.9 GHz CPU 和Nvidia GeForce GTX 1080Ti GPU,11 GB RAM;运行环境为PyTorch,CUDA,CUDNN.

3.2 实验结果与分析

3.2.1 重建性能分析

实验一不同采样率下重建结果.为了评估本文所提方法的重建性能,采用笛卡尔采样模板,分别在不同采样率下进行实验.表2 列出了本文方法、传统DIP 方法、基于CS 理论的CS-WS 方法和零填充重建在10%,20%,30%和40%采样率下的相对误差、PSNR 和SSIM 指标的数值结果.考虑到训练过程中的随机性(本文方法中网络参数的随机初始化;传统DIP 方法中网络输入和网络参数均为随机初始化),表中列出的数值结果都为运行10 次后取平均获得.由表2 中的数据对比显而易见,对于3 组MR 数据,在相同采样数据量下,本文方法具有最低的相对误差、最高的PSNR 和SSIM 值,即本文方法可获得更精确的重建结果.

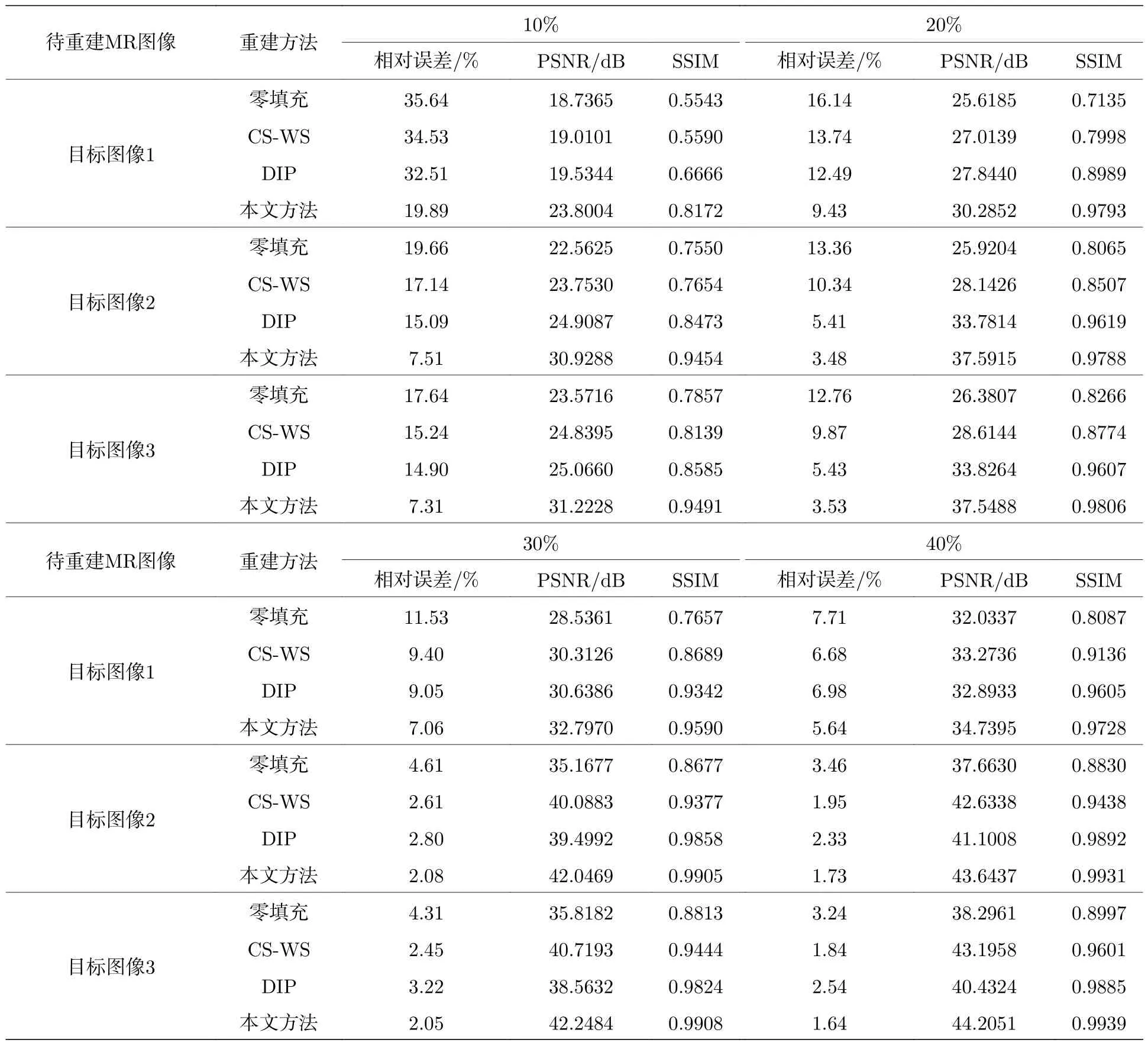
表2 笛卡尔采样模板下不同重建方法的相对误差、PSNR 及SSIMTable 2.Relative errors,PSNR and SSIM values of reconstruction by different methods under Cartesian undersampled mask.

图5 为目标图像1 的重建结果及相应的误差图,可以看出,相同采样率下,本文方法的重建误差更小,可获得更为精确的重建.

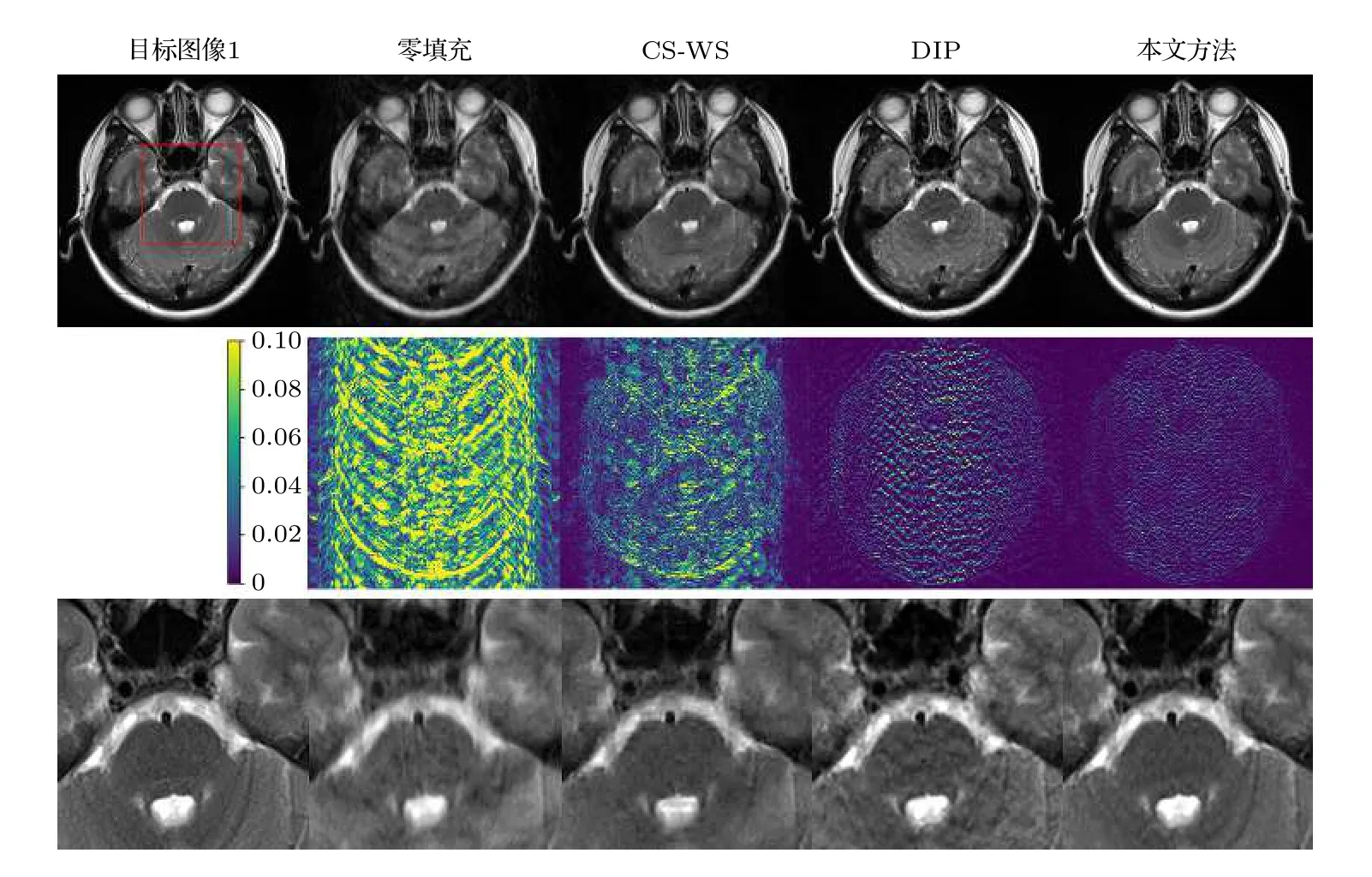
图5 笛卡尔采样模板40%采样率下目标图像1 的重建结果对比.第一行为目标图像1 与各方法重建结果,第二行为对应的误差图像,第三行为对应的局部放大图Fig.5.Comparison of reconstructions of target image 1 using Cartesian undersampled mask with 40% sampling rate:Target image 1 and reconstruction results (1st row),the corresponding error images (2nd row),and the corresponding zoom-in images (3rd row).

图6—图7 给出了目标图像2、目标图像3 在本文方法及对比方法下的重建结果.显然,本文方法在保留MR 图像中结构细节、纹理特征方面具有优势,尤其在局部放大图中更为明显.相应的误差图像也进一步表明,本文方法的重建结果误差最小,最接近目标MR 图像.

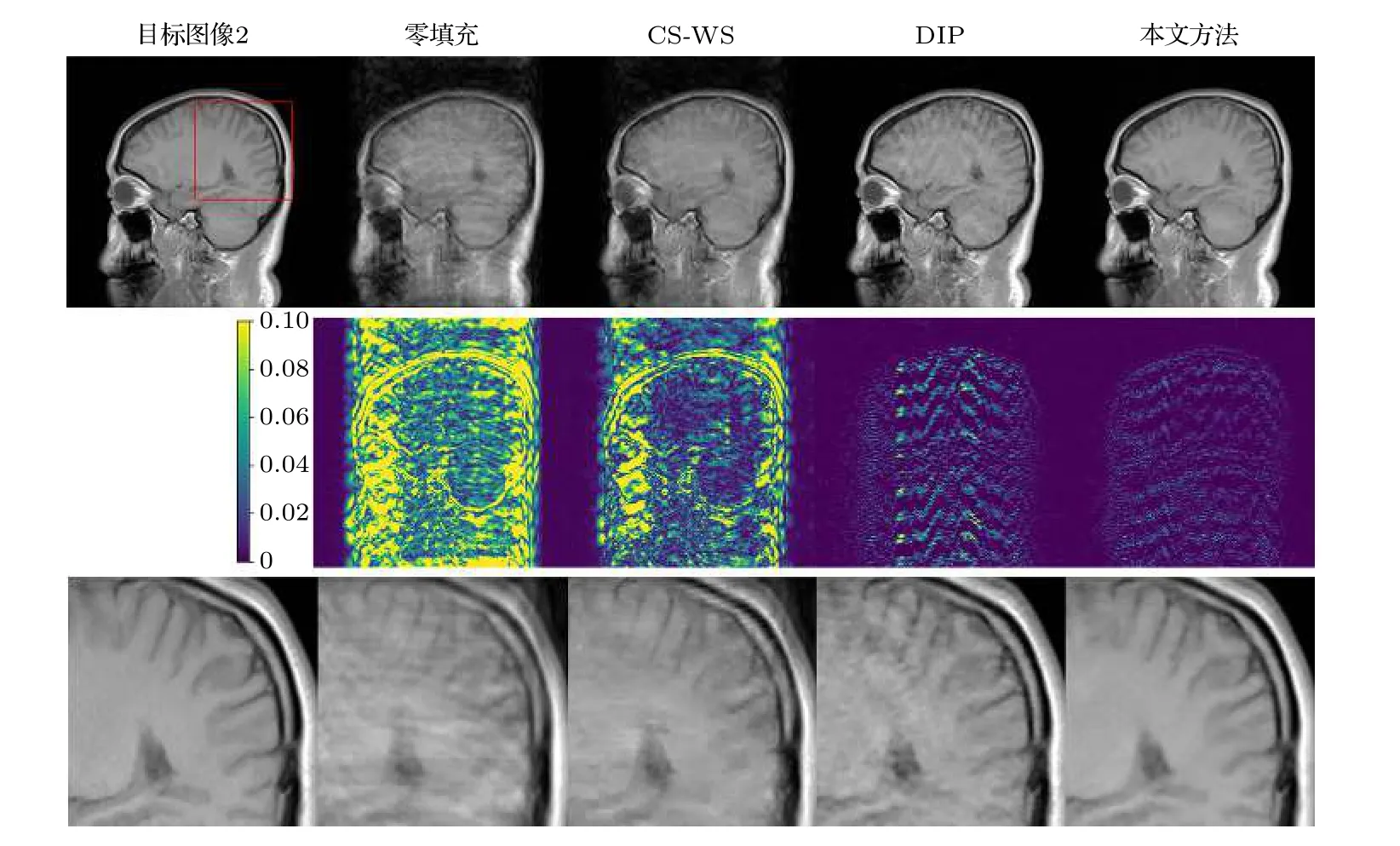
图6 笛卡尔采样模板20%采样率下目标图像2 的重建结果对比.第一行为目标图像2 与各方法重建结果,第二行为对应的误差图像,第三行为对应的局部放大图Fig.6.Comparison of reconstructions of target image 2 using Cartesian undersampled mask with 20% sampling rate:Target image 2 and reconstruction results (1st row),the corresponding error images (2nd row),and the corresponding zoom-in images (3rd row).

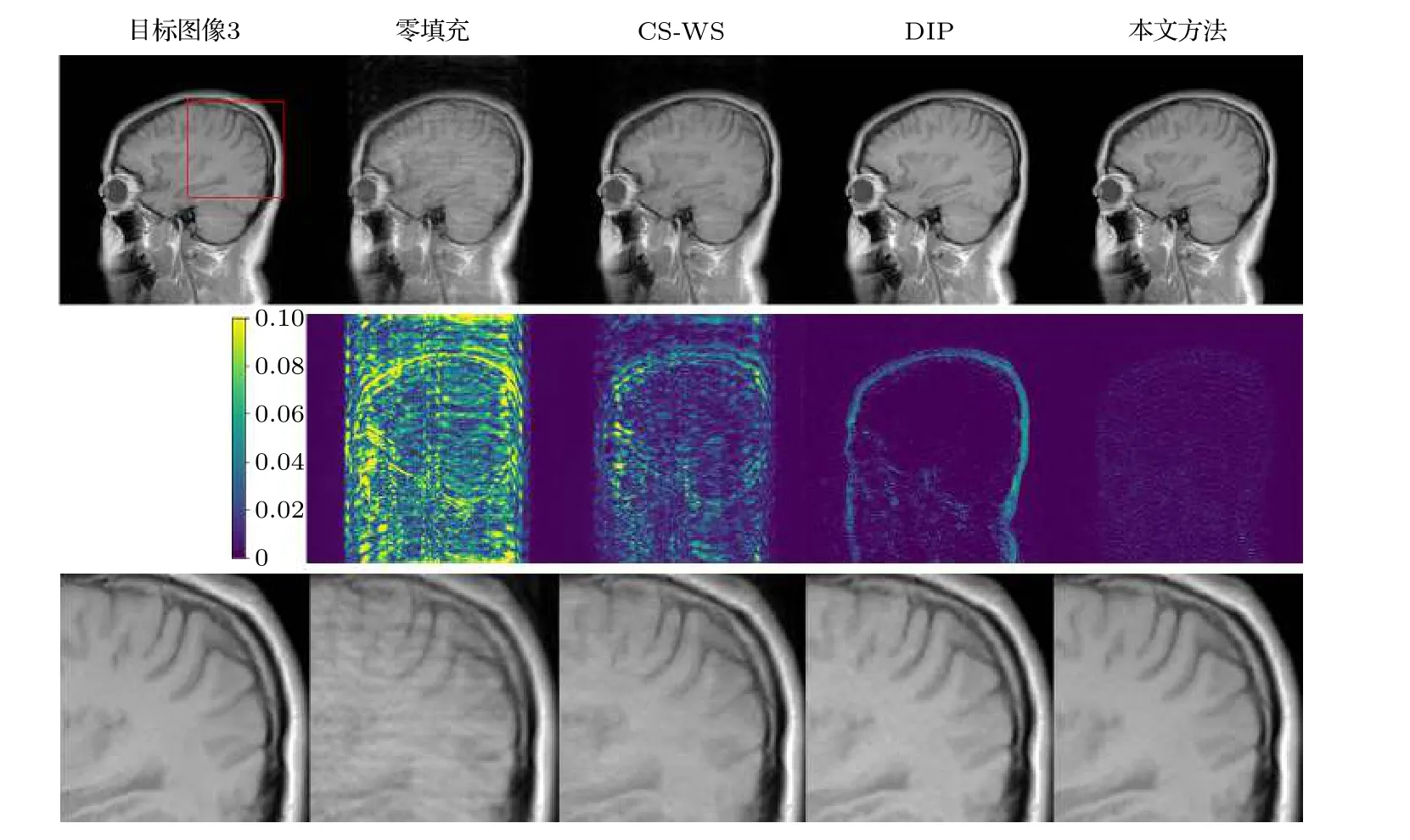
图7 笛卡尔采样模板30%采样率下目标图像3 的重建结果对比.第一行为目标图像3 与各方法重建结果,第二行为对应的误差图像,第三行为对应的局部放大图Fig.7.Comparison of reconstructions of target image 3 using Cartesian undersampled mask with 30% sampling rate:Target image 3 and reconstruction results (1st row),the corresponding error images (2nd row),and the corresponding zoom-in images (3rd row).

实验二不同采样模板下重建结果.本部分采用径向采样模板与变密度采样模板分别进行实验,评估本文方法在不同采样模板下的重建性能.本文方法与对比方法重建结果的相对误差、PSNR 和SSIM 值如表3 所列.由表中数据对比可知,本文方法在径向采样模板、变密度采样模板下的重建图像均具有更低的相对误差、及更高的PSNR 和SSIM 值,可获得更为精确的重建结果.

重建图像的视觉对比如图8—图9 所示.相应的误差图像和局部放大图表明,在径向采样模板、变密度采样模板下,本文方法的重建更为精确,能够保留更多的结构特征与细节.

图8 变密度采样模板30%采样率下目标图像1 的重建结果对比.第一行为目标图像1 与各方法重建结果,第二行为对应的误差图像,第三行为对应的局部放大图Fig.8.Comparison of reconstructions of target image 1 using variable density undersampled mask with 30% sampling rate:Target image 1 and reconstruction results (1st row),the corresponding error images (2nd row),and the corresponding zoom-in images (3rd row).

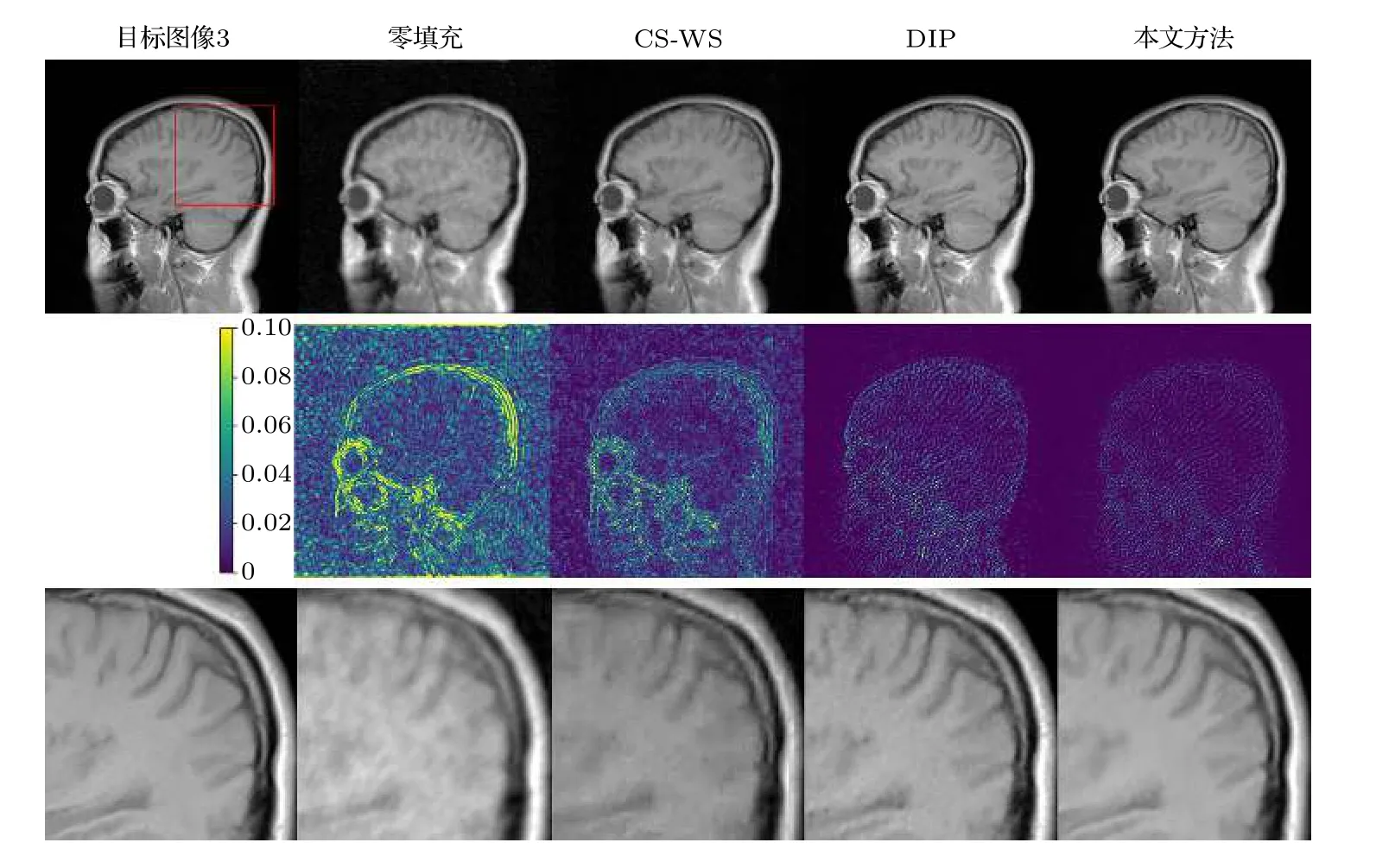
图9 径向采样模板10%采样率下目标图像3 的重建结果对比.第一行为目标图像3 与各方法重建结果,第二行为对应的误差图像,第三行为对应的局部放大图Fig.9.Comparison of reconstructions of target image 3 using radial undersampled mask with 10% sampling rate:Target image 3 and reconstruction results (1st row),the corresponding error images (2nd row),and the corresponding zoom-in images (3rd row).

3.2.2 收敛性分析

为评估本文方法的收敛性,本部分实验并画出目标图像在不同采样率下的重建误差曲线.图10中的曲线表示每100 次迭代输出重建结果的相对误差(运行10 次的平均值).从曲线可以看出,在不同的采样率下,随迭代次数的增加,相对误差逐渐收敛至一个较低的值.虽迭代过程中有轻微波动,但总体趋势保持收敛.

图10 笛卡尔采样模板下本文方法的相对误差曲线Fig.10.Relative errors curves of the proposed method under Cartesian undersampled mask.

4 讨论

4.1 消融研究

由前文多组实验结果验证,本文提出的MR 图像重建方法相较于对比方法具有重建性能的提升.为了分析验证与本文方法创新性相关的各因素对于重建性能提升的作用与贡献,本节进行消融实验.本文方法基于DIP 框架以削减对预训练及数据集的依赖,用以提升重建性能的因素有3 个.因素1:采用高分辨率参考图像作为深度网络输入,将结构先验信息引入网络;因素2:将参考图像在小波域中幅值大的系数索引集作为目标图像已知支撑集,提供支撑先验;因素3:k空间数据矫正,保证重建结果与扫描获取的k空间测量数据的完全一致性.表4 给出了目标图像1 在仅有因素1 作用下(简称DIP+Ref)、仅有因素2 作用(简称DIP+Sup)、因素1 和2 同时作用(简称DIP+Ref+Sup)以及因素1,2,3 全部作用(简称DIP+Ref+Sup+Cor) 时重建结果的量化指标数据.

结合表4 及表3 中数据可以看出,仅引入参考图像至DIP 框架可提升重建精度,仅利用参考图像获取支撑先验用于目标图像的重建,也可提升重建精度.相比而言,前者对于重建精度的提升更为显著.两者结合后,共同作用下的重建结果更加精确.从实验结果可以看出,k空间数据矫正可进一步降低重建的误差.

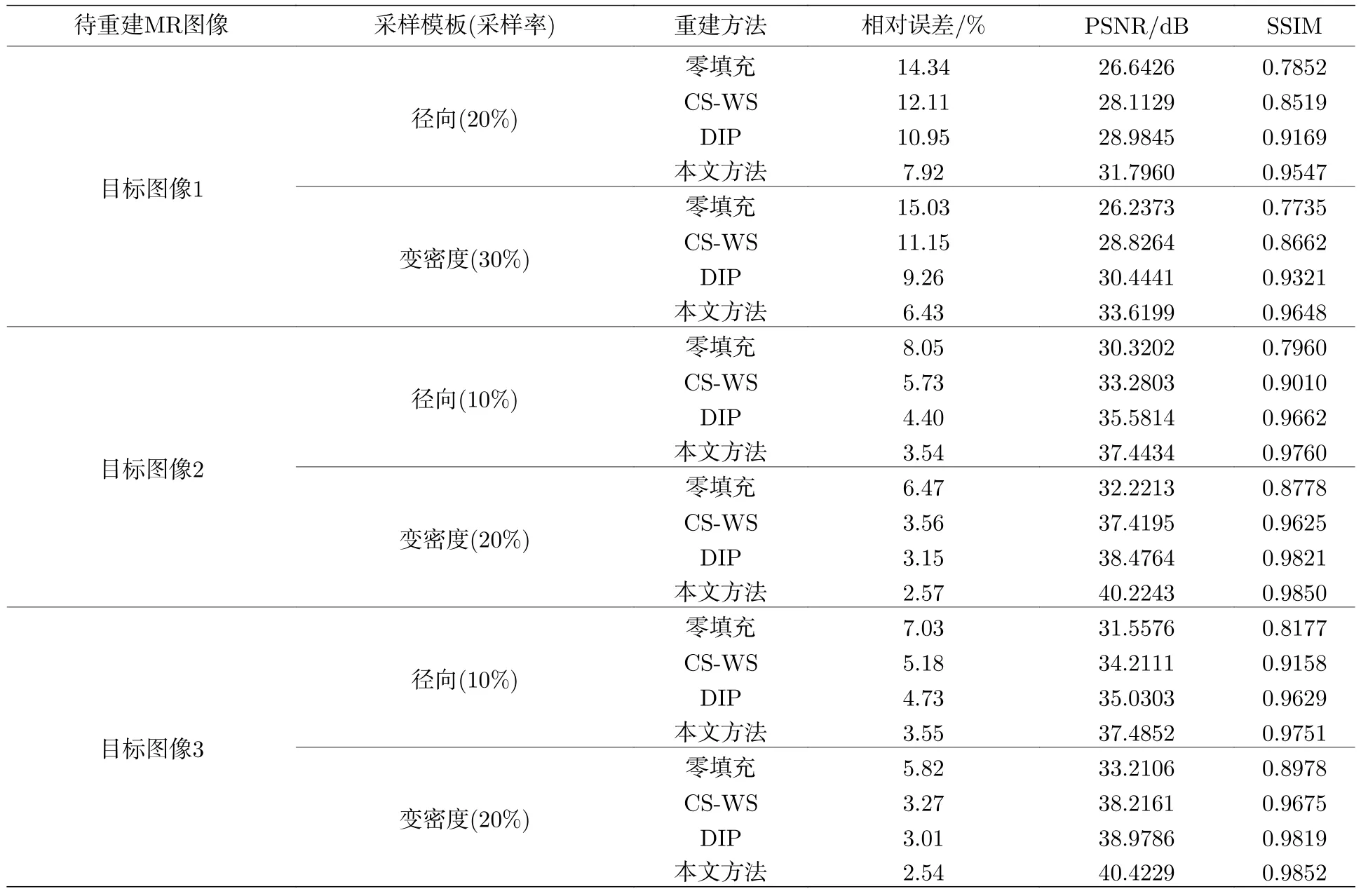
表3 径向采样模板及变密度采样模板下不同重建方法的相对误差、PSNR 及SSIMTable 3.Relative errors,PSNR and SSIM values of reconstruction by different methods under radial undersampled mask and variable density undersampled mask.

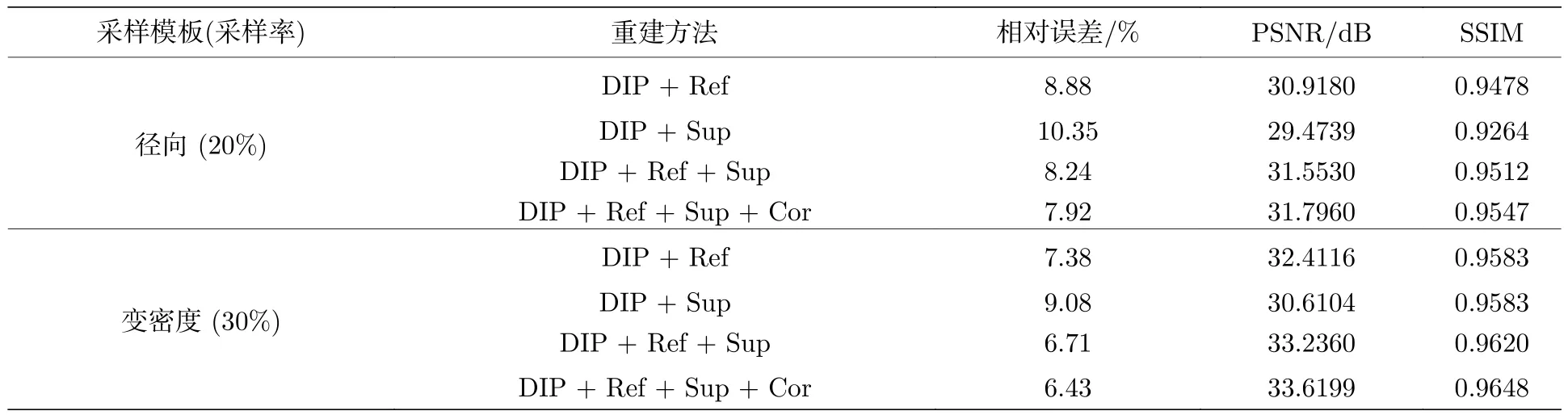
表4 径向采样模板及变密度采样模板下不同重建方法的相对误差、PSNR 及SSIMTable 4.Relative errors,PSNR and SSIM values of reconstructions by different methods under radial undersampled mask and variable density undersampled mask.

4.2 对比度差异/运动偏移下鲁棒性分析

本节主要讨论当参考图像与目标图像之间存在对比度差异及运动偏移时,本文所提方法的有效性.选取两幅对比度不同的MR 图像,如图11(a)和图11(b)所示,它们均来自3T Siemens MRI 扫描仪.成像参数分别为:(a) T2 加权图像,SE 序列,偏转角=120°,TR/TE=4000/91 ms,层厚5.0 mm;(b) T1 加权图像,GR 序列,偏转角=70°,TR/TE=250/2.5 ms,层厚 5.0 mm.以图11(a)为参考图像重建图11(b),20%笛卡尔采样下的重建结果如图11(c)所示,重建相对误差为2.19%.为了进一步验证本文方法对于运动偏移的鲁棒性,构造如图11(d)所示的目标图像,与图11(a)的参考图像相比,既有对比度差异、又存在运动偏移,20%笛卡尔采样下的重建结果如图11(e)所示,重建相对误差仅为2.54%.由此可见,本文方法对于对比度差异及运动偏移具有一定的鲁棒性.

图11 参考图像与目标图像间存在对比度差异及运动偏移情况下本文方法的重建结果 (a)参考图像;(b)待重建目标图像;(c)本文方法对(b)的重建结果;(d)待重建目标图像(存在运动偏移);(e)本文方法对(d)的重建结果;(a)—(c) 相对误差为2.19%,PSNR=40.8788 dB,SSIM=0.9937;(d),(e) 相对误差为2.54%,PSNR=39.0825 dB,SSIM=0.9937Fig.11.Reconstructions of the proposed method when there is contrast difference and motion between the reference image and the target image:(a) Reference image;(b) target image to be reconstructed;(c) reconstruction of (b) by the proposed method;(d) target image to be reconstructed(with motion effects);(e) reconstruction of (d) by the proposed method;(a)—(c) the relative error is 2.19%,PSNR=40.8788 dB,SSIM=0.9937;(d),(e) relative error 2.54%,PSNR=39.0825 dB,SSIM=0.9937.

4.3 计算效率分析

表5 给出了笛卡尔采样模板下,采样率分别为10%,20%,30%和40%时,本文方法与对比方法的计算时间.从表中数据可以看出,本文提出的方法没有节省时间.这是由于为了更新损失函数,每次迭代后的网络输出都需要进行欠采样及正则化项的运算.尽管如此,本文方法不依赖于预训练及数据集,并在重建精度上具有显著提升,这使得其依然具有一定价值及吸引力.提升本文方法的重建效率是后续研究的重要内容,将针对重建模型及进程,研究提出更为高效的重建策略及算法.

表5 笛卡尔采样下不同重建方法的计算时间Table 5.Computational time for different reconstruction methods under the Cartesian mask.

5 结论

本文提出一种新的基于深度学习的欠采样MR 图像重建方法,无需预训练、不依赖训练数据集,对临床应用具有重要意义.该方法利用参考图像与目标图像之间的结构相似性,由参考图像驱动、为目标图像的重建提供支撑先验和结构先验.将参考图像作为网络输入,以引入目标图像的结构先验至学习进程,并将参考图像在小波域中大系数的索引集作为目标图像的已知支撑集,正则化约束其补集的l1范数.实验表明,本文方法可获得更为精确的重建结果,且在保持组织边缘与细节方面更具优势.