Bessel 型光晶格中自旋-轨道耦合极化激元凝聚的稳态结构*

陈海军 任元 王华

1) (航天工程大学宇航科学与技术系,北京 101416)

2) (航天工程大学基础部,北京 101416)

3) (航天工程大学,激光推进及其应用国家重点实验室,北京 101416)

1 引言

固体中的玻色子和光子在两者能量和动量接近时发生强耦合时形成的准粒子称之为极化激元,激子是电子和空穴(带正电)由于库仑力的作用形成的束缚态.激子-极化激元是指半导体微腔中的光子和内嵌在微腔量子阱中的激子发生强耦合形成的准粒子[1],是一种半光半物质的状态,是激子和光子的叠加态,具有 10-31量级的质量和ps 量级的寿命,其中的激子部分容易和其他粒子产生相互作用[2].激子-极化激元彼此之间发生相互作用,形成复合玻色子,可在接近室温的条件下经历类似于玻色-爱因斯坦凝聚(Bose-Einstein condensates,BECs)的非平衡相变,称之为激子-极化激元BEC(简称为极化激元凝聚,polariton condensates)[3-6].

原子除了轨道角动量l外,还有自旋角动量s,轨道角动量和自旋角动量的耦合称为SO 耦合(spinorbit coupling,SOC)或者s-l耦合,SOC 是量子力学诞生之初就已知的一种现象,代表了磁原子内相互作用的主要来源[7].SOC 引起了原子能谱的变化,进而导致了原子能谱的精细结构的形成.在中性原子中,不存在SOC 作用[8],但是可以通过适当修改原子和光之间的相互作用产生非Abelian规范势[9],从而使中性原子受到SOC 作用[10].

在固体物理中,SOC 作用是许多基本效应的起源[11],由晶体结构决定,很难操纵,而且很难与其他影响分开.在没有反转对称性的半导体中,晶体中的静电场通过Lorentz 变换成运动电子坐标系中的磁场,进而和电子自旋耦合,产生SOC 作用[12].在能用单离子完美描述的固体磁性方面,SOC 起着重要作用,如在稀土绝缘体中和半导体中,在极值点附近SOC 通常会引起能带分裂[7],另一方面,SOC 通过耦合自旋和轨道运动自由度来提升单电子能级的简并性[13].

在极化激元凝聚中,可以通过极化激元能级的腔诱导TE-TM 分裂实现足够强的SOC[14].SOC对于具有旋量序参数的多组分旋量BEC 系统的拓扑结构有十分重要的作用,在四分量旋量BEC 系统中,发现了依赖于自旋的明暗激子转换,发现SOC产生了丰富多样的拓扑元素,观察到了明暗激子的相分离以及密度和自旋极化的奇异空间结构[11].在原子BEC 中,SOC 会极大地影响周期势场中可用非线性激发的稳定性和对称性[15].基于此,文献[16]研究了双组分旋量极化激元凝聚中,周期势场中SOC 对能隙极化激元基本孤立子和涡旋孤立子形成的影响,给出了4 个不同族,拓扑荷数为m=±1的稳定的涡旋孤立子.文献[17]研究了径向周期势场中自旋极化激元凝聚的演化,在该周期势场中允许新的非线性激发,并支持极化激元凝聚体中以前从未证明过的各种动态稳定孤立子状态,包括密度峰值位于不同径向最小值的环状孤立子和扩展的动态稳定多环模式.

事实上,将光晶格势场引入非线性介质显著提高了BEC 中局域波结构的稳定性[18].上述文献中研究了周期势场中极化激元凝聚中局域波结构及其稳定性,除此之外,非周期性势场中极化激元凝聚的相关研究也引起了人们的关注,非周期性势场最经典的例子是Bessel 型光晶格(Bessel lattice,BL).BL 可由非衍射Bessel 光束产生,Bessel 光束或称为无衍射光束由Durnin[19]于1987 年首先提出,可由计算机生成的全息图[20]或者锥形棱镜[21]产生.由于晶格诱导场的衍射受到抑制,类似于谐波晶格的情况,使得这种柱对称的径向非周期的晶格显得特别重要.

物质波孤立子是一种重要的非线性局域态,能长时间保持形状和能量不随时间变化,包括明孤立子、暗孤立子和涡旋孤立子等.有很多理论工作研究了BL 中孤立子的类型、结构、稳定性和动力学行为.在散焦立方非线性介质中,由BL 可以支持静态的、旋转多极模孤立子和多环结构多极模孤立子[22].在自聚焦介质中由BL 可以支持稳定的三维孤立子,如果晶格强度超过某一阈值,孤立子在其范数的一个或两个区间内是稳定的[23].在立方-五次方非线性介质中,BL 可以支持涡旋孤立子、多极孤立子和“项链”形孤立子[24].在立方非线性介质中,BL 可以支持在自然界中非常罕见的、具有明亮形状的、稳定的环形涡旋孤立子,由于BL 的存在,这种环形涡旋孤立子是动态稳定的[22].Kartashov等[25]研究了BL 中涡旋孤立子家族的显著特性,并给出了它们的稳定性条件,结果表明,孤立子拓扑荷数越高,使其稳定所需的晶格深度越大.另外,BL 中线性和非线性情况下基础孤立子和多极孤立子的稳定性被研究,在线性情况下,通过数值方法求解了不同深度的BL 对应的本征值和本征函数,在非线性情况下,研究了基础孤立子和多极孤立子的存在性和稳定性[26].

综上所述,本文将BL 势场引入极化激元凝聚系统,研究在BL 势场囚禁下双组分旋量极化激元凝聚系统的稳态结构.第2 节首先介绍了BL 势场的数学模型及其基本特征,然后给出了描述双组分旋量极化激元凝聚系统的GP (Gross-Pitaevskii)方程,并阐述了GP 方程中各参数的物理意义及其取值范围,最后介绍了求解GP 方程的数值算法.第3 节研究了实验室坐标系中极化激元凝聚的稳态结构.第4 节研究了旋转坐标系中极化激元凝聚的稳态结构.第5 节研究了BL 势场中多极孤立子的旋转稳定性.最后,第6 节给出了主要结论.

2 模型和方程

本节首先介绍BL 势场的数学模型及其主要特点,然后给出描述极化激元凝聚动力学的主要方程,并阐述方程中各参量和函数的物理意义和取值范围,最后介绍求解方程的数值方法.

2.1 Bessel 型光晶格

图1 不同阶数n 的Bessel 型光晶格势场的空间分布(a) n=0;(b) n=1;(c) n=2;(d) n=3 .x,y ∈[-8,8].势场的数学表达式为其中V0=1,b=0.5Fig.1.The BL potentialwith different n:(a) n=0;(b) n=1;(c) n=2;(d) n=3 .x,y ∈[-8,8],V0=1,b=0.5.

高阶(n≥1) BL 的最小值分布在靠近势场中央(势场中央是势垒)的第一圆环处(图1(b),(c),(d)中黑色部分),第一圆环的半径随阶数n的增大而增加,其深度随阶数n的增加而减小,高阶BL 在第一圆环处形成环状浅势阱,其特点是在中央存在“倒钟形”势垒.高阶BL 中,除第一圆环外,其他圆环都由环状势垒彼此分割.因此,为了维持相同的势阱深度,高阶BL 需要更大的势阱强度.需要指出的是,中央深势阱和环状浅势阱的宽度可以通过径向收缩因子b调节,在没有特别指出的情况下,计算过程中均取b=0.5.另外,高阶BL 的势阱深度和势场强度不一致,势阱深度由势场最小值和势场强度共同决定.如n=3 时,势场最小值为-0.2,为了维持和n=0 时具有相同的势阱深度,其势场强度应取V0=5.

2.2 Gross-Pitaevskii 方程

由于极化激元具有有限寿命以及极化激元之间存在散射,因此极化激元凝聚是非平衡系统[27],其动力学通常用由衰减和泵浦引起的非厄米平均场近似理论描述[28].但是,如果极化激元凝聚达到稳定状态,其中的泵浦和衰减达到动态平衡,可以看成是准保守系统[16].另外,在自旋极化激元凝聚系统中,包含两种自旋特征的分量,假定描述双组分极化激元凝聚系统的波函数为ψ=(ψ1,ψ2)T,其满足的Gross-Pitaevskii 方程的无量纲形式为[14,29]无量纲过程中,空间、时间和能量单位分别是x0=1 μm,t0=1.9ps 以及ε0=0.35 meV[16].势能项α表示由腔诱导TE-TM分裂引起SO 耦合强度[30].g1=g2=1 表示同种自旋组分内部极化激元之间存在排斥相互作用.g12=-0.05表示两种自旋组分极化激元之间存在微弱的吸引相互作用,由于组分之间的相互作用十分微弱,因此组分之间的相互作用对系统稳态结构不起决定作用.

考虑到要计算极化激元凝聚由于旋转引起的稳态结构,以及稳态结构在旋转过程中随时间的演化情况,因此选取旋转坐标系 (x′,y′) 是十分方便的,具体旋转方案可以参考文献[31].旋转坐标系和实验室坐标系 (x,y)之间的关系为x′=xcos(Ωt)+ysin(Ωt),y′=ycos(Ωt)-xsin(Ωt),其 中Ω表 示旋转坐标系相对于实验室坐标系的旋转角速率.在不至于混淆的前提下,采用相同的符号x,y表示两种坐标系,如果Ω=0表示实验室坐标系,Ω/=0表示旋转坐标系.在旋转坐标系中,会在方程(1)中 引 入-Ωz项[32,33],其 中(ℏ=1)表示角动量z方向分量算符,则-Ωz=iΩ(x∂y-∂x).

2.3 计算方法和参数选择

为了得到系统的稳态结构,利用虚时演化方法[34]求解方程(1).虚时演化方法求解方程(1)需要选择合适的初始条件,虽然初始条件的选择不会影响最终稳态结构,但是合适的初始条件会使得计算程序尽快地收敛到最终的稳态结构[35].在实验室坐标系中,常见的初始条件包括高斯型波包和TF近似求解方程(1)得到的解析解.在旋转坐标系中,初始条件的选择没有确定的结论,文献[35]提出了高斯型波包和量子化涡旋的叠加态作为初始条件,叠加态中的比例系数分别是 1-Ω和Ω.

为了计算多极孤立子稳态结构,本文采用了正反涡旋叠加态[36]

作为初始条件,其中α,β是实数,使得α2+β2=1,其平方表示正反涡旋在叠加态中所占的比重,为了方便,取w是高斯波包的宽度,l1和l2分别表示正反涡旋的角动量量子数,对应的角动量分别是l1ℏ,l2ℏ.

势场结构和系统参数对稳态结构有重要影响.BL 的两个参数分别是势场强度V0和径向收缩因子b,通过调节这两个参数,可以改变势场的结构,进而在其中形成对应的稳态结构.系统参数包括组分之间极化激元间的相互作用和组分内部极化激元间的相互作用,以及SOC 相互作用,在本文计算过程中,固定g1=g2=1,g12=-0.05,即组分内部有较强的排斥相互作用,而组分之间只有微弱的吸引相互作用,即可调节的系统参数只有SOC 相互作用.另外,旋转参考系的旋转角速率在旋转参考系中也是重要的参数,其取值范围选择Ω ∈[0,1].

3 实验室坐标系中极化激元凝聚的稳态结构

本节在实验室坐标系中求解无SOC 作用和有SOC 作用时极化激元凝聚的稳态结构.

3.1 无SOC 作用时实验室坐标系中极化激元凝聚的稳态结构

实验室坐标系中,Ω=0.首先计算0 阶Bessel势场(n=0)中极化激元凝聚的稳态结构,该势场在中央形成深势阱,中央深势阱类似于抛物型势阱,又不完全相同于抛物型势阱,中央深势阱的深度可以通过势场强度调节,而抛物型势阱是无限深势阱.0 阶Bessel 势场(n=0)中的稳态结构如图2所示,图2(a)给出的是高斯型孤立子密度分布,高斯型孤立子属于抛物型势阱对应的本征态,属于基础孤立子类型,维持高斯型孤立子的势场强度是V0=1.图2(b)和图2(c)表示多极孤立子密度分布,分别对应偶极和四极孤立子,可以看出,维持多极孤立子需要更大的势场强度,由于0 级Bessel势场的中央深势阱深度和势场强度一致,即维持多极孤立子需要更深的中央势阱.假定多极孤立子的极 数 用np表 示,则np=2时,V0=4;np=4 时,V0=20,随着极数的增加,势场强度增大,而且在中央深势阱中很难支撑极数较大的多极孤立子,即使势场强度再大.图2(c)的计算范围是x,y ∈[-3,3],而图2(a)和图2(b)的计算范围是x,y ∈[-8,8],可以看出,随着势场强度的增加,多极孤立子越来越局域化,占据的空间范围越小,与之对应的密度分布的最大值随之增加.另外需要指出的是,多极孤立子相邻极对应的相位是反相的,图2(d)所示是和图2(c)对应的相位分布,可以看出,相位在0 和π之间交替变化.

图20 阶BL 中央深势阱中的(a)高斯型孤立子、(b)偶极孤立子和(c)四极孤立子的密度分布;(d)与图(c)对应的相位分布.图(a)和图(b)的计算范围是 x,y ∈[-8,8],图(c)和图(d)的计算范围是 x,y ∈[-3,3],BL 参数分别是(a) V0=1;(b)V0=4,b=0.4;(c),(d)V0=20Fig.2.Densities of (a) Gassian,(b) dipolar,(c) quadrupolar solitons and (d) the phase of the quadrupolar soliton in the central deep potential well of the BL,where x,y ∈[-8,8]for panels (a) and (b),x,y ∈[-3,3]for panels (c) and (d).Values of other parameters are V0=1for panel (a),V0=4,b=0.4for panel (b),V0=20 for panels (c) and (d).

除中央深势阱外,环状浅势阱的特点是深度随着Bessel 晶格势场阶数n的增加而减小,半径随着阶数n的增加而增加.环状浅势阱中极化激元凝聚的稳态结构如图3 和图4 所示.图3 给出的是环状孤立子,可以看出,浅势阱中环状孤立子的结构完全依赖于环状势阱,其半径随着阶数n的增加而增大.维持稳定环状孤立子结构的势场强度随着阶数n的增大而增加.另外,由于本文选择保守系统,粒子(极化激元,下同)数应该守恒,随着BL 阶数n的增加,分布范围(环形宽度不变,半径增加)随之增加,因此环状孤立子的最大密度随着阶数n的增加而减小.环状浅势阱中极化激元凝聚的多极孤立子稳态结构如图4 所示,和中央深势阱相比,环状势阱中央存在势垒,可以阻止粒子向中央移动,更易于多极孤立子的形成.图4 给出多极孤立子的极数np=2,4,6,8,10,12,可以看出,极数是偶数.实际上,这种多极孤立子可以看成是正反涡旋的叠加态,当l1=l2=l时,形成叠加态的极数是 2l,此时正反涡旋的角动量彼此抵消,整体的角动量为0,如果l1/=l2,可以形成极数为奇数的叠加态,但是l1/=l2,整体叠加态有剩余净角动量,因此稳定的多极孤立子是极数为偶数、整体角动量为0 的稳态结构.

图3 BL 环状浅势阱中极化激元凝聚环状孤立子稳态结构的密度分布 |ψ1,2|2随阶数n 的变化,计算范围 x,y ∈[-8,8],角速率Ω=0,SOC 作用强度 α=0.BL 参数分别是 (a) V0=10,n=1;(b) V0=10,n=2;(c)V0=20,n=3Fig.3.Densities |ψ1,2|2of ring-shaped solitons in the ring-shaped shallow potential well of the BL with different (V0,n) :(a) (10,1);(b) (10,2);(c) (20,3).x,y ∈[-8,8],Ω=0,α=0.

图4 BL 环状浅势阱中极化激元凝聚多极孤立子稳态结构的密度分布 |ψ1,2|2,计算范围 x,y ∈[-8,8],角速率 Ω=0,SOC 作用 强 度 α=0,n=3 .V0 和 np分 别 是 (a) V0=30,np=2;(b) V0=30,np=4;(c) V0=30,np=6;(d) V0=60,np=8 ;(e) V0=60,np=10;(f)V0=70,np=12Fig.4.Densities (|ψ1,2|2) of multipole solitons in the ring-shaped shallow potential well of BL with different (V0,np) :(a) (30,2);(b) (30,4);(c) (30,6);(d) (60,8);(e) (60,10);(f) (70,12).x,y ∈[-8,8],Ω=0,α=0,n=3.

另外,在同一阶数的Bessel 势场中可以形成极数不同的多极孤立子,图4 中BL 势场的阶数是n=3,可以看出,多极孤立子的极数np随着势场强度的增加而增大,较大极数的多极孤立子需要较强的势场强度,即某一势场强度能维持多极孤立子的极数是确定的.如V0=30 维持的多极孤立子的最大极数是np=6,V0=60 维持的多极孤立子的最大极数是np=10,而当np=12 时,需要的势场强度V0=70.另外,需要指出的是,同一势场强度可以维持不同极数的多极孤立子,势场强度和极数之间并没有一一对应的关系.如V0=30 可以维持np≤6的多极孤立子,V0=60可以维持np≤10 的多极孤立子,V0=70至少可以维持np≤12 的多极孤立子.最后,多极孤立子各极的最大密度随np没有较大变化,在Bessel 势场环状浅势阱中形成的多极孤立子各极随角度均匀分布,边缘清晰,各极所占空间范围随着np的增加而减小.相位分布和图2(d)结果一致,多极孤立子相邻极相位反相,相位在0 和 π 之间交替变化.

3.2 SOC 作用对实验室坐标系中极化激元凝聚稳态结构的影响

图5 和图6 给出了存在SOC 作用时实验室坐标系中极化激元凝聚的稳态结构.图5 给出了SOC作用对中央深势阱中基础孤立子结构的影响,不存在SOC 作用时,基础孤立子呈柱对称分布,当出现SOC 作用时,基础孤立子在y方向被压缩,随着SOC 作用系数α的增加,这种压缩趋势变得强烈,基础孤立子的中心密度也随之增加,如图5(a),和图5(b)所示.当SOC 作用系数α继续增加,如接近0.5 时,基础孤立子在x方向和y方向同时被压缩,y方向压缩的程度更大,如图5(c)所示.当α非常接近0.5 时,基础孤立子开始分裂,除了中央主要部分外,有少部分粒子围绕在中央部分外侧,并且关于x轴分离对称,如图5(d)所示.

图5 BL 势场中央深势阱中基础孤立子稳态结构的密度分布 |ψ1,2|2随SOC 作用强度α 的变化 (a) α=0.3;(b) α=0.4 ;(c) α=0.495;(d) α=0.499.计算范围 x,y ∈[-3,3],BL 参数为 V0=1.0,n=0,角速率Ω=0Fig.5.Densities |ψ1,2|2of fundamental solitons in the central deep potential well of the BL with different α:(a) α=0.3 ;(b) α=0.4;(c) α=0.495;(d) α=0.499.x,y ∈[-3,3],Ω=0 ,V0=1.0,n=0.

图6 给出了SOC 作用对环状浅势阱中环状孤立子的影响,可以看出,相同强度的SOC 作用对不同阶数Bessel 光晶格势场中环状孤立子结构的影响一致,使得不存在SOC 作用时的完全柱对称的环状孤立子结构在y方向发生分裂,分裂间隙随着阶数n的增大而增加.从稳态结构的密度分布可以看出,SOC 作用影响下的稳态结构类似于偶极孤立子,但是从相位图6(d)可以看出,该稳态结构的相位图完全不同于偶极孤立子的相位分布,相位分布的极数是密度分布极数的2 倍,相邻极所对应的相位在0 和约 0.86 之间交替变化,而偶极孤立子的相位在0 和 π 之间交替变化.

图6 存在SOC 作用时,不同阶数BL 势场环状浅势阱中极化激元凝聚稳态结构的密度分布 |ψ1,2|2.计算范围 x,y ∈[-8,8],角速率 Ω=0,SOC 作用强度 α=0.2.BL 参数分别是 (a) V0=10,n=1;(b) V0=10,n=2;(c),(d)V0=20,n=3Fig.6.In the presence of SOC,the densities (|ψ1,2|2) of stationary state structures in the ring-shaped shallow potential well of the BL with different V0 and n:(a) V0=10,n=1;(b) V0=10,n=2;(c),(d) V0=20,n=3 .x,y ∈[-8,8],Ω=0,α=0.2.

4 旋转坐标系中极化激元凝聚系统的稳态结构

研究旋转坐标系中极化激元系统的运动时,实验室坐标系是静系,旋转坐标系相对于静系以角速率Ω旋转是动系.旋转坐标系中的稳态结构指的是观察者处于动系中时观察到的极化激元凝聚的密度分布,根据运动的相对性,这种密度分布也可以看成是旋转坐标系不动,而极化激元凝聚旋转引起的,其旋转角速率是-Ω.

4.1 旋转坐标系中环状浅势阱中的涡旋孤立子

为了讨论极化激元凝聚系统的旋转状态,引入了旋转坐标系(x′,y′),其旋转角速率是Ω.在旋转参考系中,可以得到涡旋孤立子.图7 给出了不存在SOC 作用时环状浅势阱中涡旋孤立子的稳态结构,可以看出,不存在SOC 作用时,两种组分形成对称的稳态结构,即|ψ1|2=|ψ2|2,上述实验室坐标系中的稳态结构皆是如此.由于受到环状浅势阱的束缚,环状涡旋孤立子和环状孤立子的密度分布相同,从密度分布上不能区分是环状孤立子还是环状涡旋孤立子.图7(a)表示旋转坐标系角速率Ω=0.05时形成的涡旋孤立子的密度分布,图7(b)表示与之对应的相位分布,可以清楚地看出,涡旋孤立子中涡旋对应相位分布中的奇点,相位围绕奇点从0 到 π 均匀变化.图7(b)表示旋转坐标系角速率Ω=0.1 时形成的涡旋孤立子的密度分布,图7(d)表示与之对应的相位分布,可以看出,相位在奇点周围经历了两次从0 到 π 的均匀变化,这种变化次数和环状涡旋孤立子对应的角动量成正比,角速率为0.1 时对应涡旋孤立子的角动量是角速率为0.05时形成涡旋孤立子角动量的2 倍.

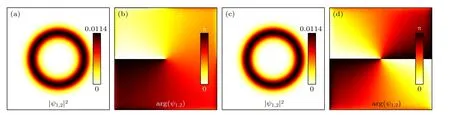
图7 无SOC 作用,旋转坐标系中,处于BL 环状浅势阱中极化激元凝聚的涡旋孤立子结构的密度((a),(c))和相位((b),(d))分布,BL 参数为 V0=10,n=3,计算范围 x,y ∈[-8,8],α=0.角速率分别是0.05((a),(b))和0.1((c),(d))Fig.7.In the absence of SOC,the densities ((a),(c)) and phases ((b),(d)) vortex solitons in the ring-shaped shallow potential well of the BL in the rotating coordinate frame with different Ω (0.05 for panels (a) and (b),and 0.1 for panels (c) and (d)),where x,y ∈[-8,8],α=0 ,V0=10,n=3.

图8 是存在SOC 作用时,环状浅势阱中涡旋孤立子的稳态结构.可以看出,当存在SOC 作用时,两组分之间发生了组分分离,这和无SOC 作用系统的组分分离条件是不一致的,无SOC 作用系统的组分分离条件是＞g1g2[37],而本文所给的参数并不满足这一条件,因此在存在SOC 作用的系统中,由于SOC 作用的存在,不满足条件1g2时,组分之间也发产生了分离.另外可以看出,当系统中存在SOC 作用时,在旋转坐标系中,环状浅势阱中两组分形成不对称的(|ψ1|2/=|ψ2|2)稳态结构.

图8(a)表示旋转角速率为Ω=-0.15 时环状浅势阱中的极化激元凝聚的稳态结构.第一组分的密度分布|ψ1|2呈现类似于偶极孤立子的结构,偶极孤立子的两极关于x轴分离对称.|ψ1|2对应的相位分布呈不规则的区域显示,每个区域内相位是从0 到 π 变化,但是每个区域的边缘不规则,而且每个区域对应的相位奇点也不重合.第二组分的密度分布|ψ2|2也呈现类似于偶极孤立子的分布,但是两极没有完全分离,关于y轴对称,相位分布和第一组分具有相同特点.整体上看,两个组分发生了组分分离,第一组分上下布局,第二组分左右布局.

图8 存在SOC 作用时,不同角速率下形成的涡旋孤立子的密度和相位分布 (a) —0.15;(b) 0;(c) 0.15.计算范围x,y ∈[-8,8],α=0.1 ,V0=10,n=3Fig.8.In the presence of SOC,the densities and phases of vortex solitons in the ring-shaped shallow potential well of the BL with different Ω :(a) —0.15;(b) 0;(c) 0.15.x,y ∈[-8,8] ,V0=10,n=3,α=0.1.

图8(b)表示旋转角速率为0 时环状浅势阱中的稳态结构,两组分呈对称分布,即|ψ1|2=|ψ2|2,其特点在第3.1 节做了分析,两组分的相位分布相差 π/2 角度,即第二组分的相位分布相对于第一组分的相位旋转了 π/2 角度.图8(c)表示旋转角速率为Ω=0.15 时环状浅势阱中的稳态结构,和图8(a)的旋转方向相反,可以看出,由于SOC 作用的存在,相比于图8(a),两组分的密度和相位分布刚好完全交换.因此,对于存在SOC 作用的体系,环状浅势阱中涡旋孤立子的基态结构对于角速率不是完全对称的,而是反对称的,即|ψ1(Ω)|2=|ψ2(-Ω)|2,|ψ2(Ω)|2=|ψ1(-Ω)|2.

4.2 BL 的径向缩放因子对旋转系统稳态结构的影响

如上所述,当存在SOC 作用时,在环状浅势阱中的涡旋孤立子会产生组分分离使系统形成非对称的稳态结构,这种组分分离现象在实验室坐标系中并不会产生,在实验室坐标系中形成对称的稳态结构.本节讨论坐标系高速 (Ω ≈1) 旋转情况下,BL 势场的径向缩放因子b对中央深势阱中涡旋稳态结构的影响,缩放因子可以通过调节深势阱的宽度改变势场的结构进而影响稳态结构.

图9(a)给出了b=0.1 时系统的稳态结构,b的数值越小,势阱宽度越大,可以看出,两组分发生了完全的柱对称组分分离,组分1 占据深势阱的中央位置,而组分2 环绕在组分1 周围,而且组分1 的密度最大值远大于组分2 的密度最大值,1.405/0.1289≈11,即组分1 的密度最大值大约是组分2 密度最大值的11 倍.

图9(b)给出了b=0.2 时系统的稳态结构,随着b值的增加,势阱宽度减小,囚禁范围减小,可以看出,两组分所占据的空间范围减小,两组分的主要部分(密度分布较大的区域)也发生了组分分离,组分1 的密度空间分布没有很大变化,而相位分布有了变化,独立的4 个相位区域均匀分布,相位大小交替变化.组分2 的主要部分形成了上下对称的偶极孤立子形式,而其余部分在中央形成了相邻的两个涡旋,在相位图上可以清楚地看出,两组相位从0 到 π 变化区域,但是相位奇点没有完全重合.

图9 BL 势场的径向缩放因子b 对中央深势阱中涡旋稳态结构的密度和相位的影响 (a) b=0.1;(b) b=0.2;(c) b=0.3 ;(d) b=0.4.计算范围 x,y ∈[-2,2],SOC 作用强度 α=0.4,BL 参数为 V0=40,n=0,旋转角速率Ω=0.95Fig.9.Densities and phases of stationary vortex structures in the central deep potential of the BL with different b:(a) b=0.1 ;(b) b=0.2;(c) b=0.3;(d) b=0.4.x,y ∈[-2,2],α=0.4 ,V0=40,n=0,Ω=0.95.

图9(c)给出了b=0.3 时系统的稳态结构,随着b值继续增加,势阱宽度继续减小,囚禁范围继续减小,可以看出,两组分所占据的空间范围进一步缩小,整体上看,两组分没有完全组分分离,两组分都在深势阱中央部分有分布,组分1 全部分布在势阱中央部分,而组分2 呈“纺锤”型沿着y方向分布,沿x方向有两个涡旋对称分布.两组分的相位分布相对于图9(b)没有显著变化.

图9(d)给出了b=0.4 时系统的稳态结构,两组分的密度分布相对于图9(c)无显著变化,只是组分2 的“纺锤”型分布沿y方向.组分1 的相位分布由反对称的上下两部分构成,组分2 的两个从0 到 π 的相位变化区域奇点关于x轴分离对称分布.

5 BL 势场中多极孤立子的旋转稳定性

第3 节给出了实验室坐标系中,在Bessel 势场的中央深势阱和环状浅势阱中可以形成多极孤立子,由于环状浅势阱存在中央势垒,能阻止粒子向势场中心靠拢,从而更容易形成多极孤立子.第4 节研究了旋转坐标系中涡旋孤立子的稳态结构.本节研究第3 节中给出的多极孤立子的稳定性,即让多极孤立子以一定的角速率长时间旋转,检验其保持整体性的能力.

检验多极孤立子稳定性的一个有效方法是观察其长时间演化行为,如果其密度分布的整体性和相对结构不随时间变化,则极化激元凝聚系统是稳定的,否则系统是不稳定的.图10 为旋转角速率为Ω=0.1时,几种模式的多极孤立子在t ∈[0,100]区间内旋转的过程中其密度分布随时间的变化.图10(a)和图10(b)表示的是在中央深势阱中形成的偶极和四极孤立子密度分布随时间的演化情况.从图10(a)可以看出,中央深势阱中形成的偶极孤立子在长时间的旋转演化过程中密度分布的相对位置和结构保持不变,偶极孤立子是旋转稳定的.为了观察其旋转细节,给出了时间间隔 Δt=25 时的密度分布,可以看出,偶极孤立子整体做类似于刚体的匀速旋转运动,更进一步证实了其稳定性.

图10(b)给出了中央深势阱中形成的四极孤立子的旋转情况,可以看出在t ∈[0,22.5]区间内保持完整的刚体匀速旋转运动,但是,当t=30 时,四极孤立子突然塌缩.一方面,在Bessel 势场的中央深势阱中很难形成极数较多的多极孤立子,如在本文给定的条件下,形成了np=2 的偶极孤立子;另一方面,在Bessel 势场的中央深势阱中形成的极数较多的孤立子是不稳定的,如本文给定的条件下,偶极孤立子是稳定的,而四极孤立子是不稳定的.

图10(c),(d)给出了Bessel 势场中环状浅势阱中形成的多极孤立子的旋转过程.图10(c)表示环状浅势阱中四极孤立子在t ∈[0,100]区间内旋转过程中密度分布随时间的变化过程,同样地,给出时间间隔 Δt=25 时的密度分布,可以看出,旋转过程中,四极孤立子保持了整体的刚性匀速旋转,密度分布的四极之间的相对位置没有变化,密度分布的最大值也保持恒定.

图10 BL 势场中多极孤立子在旋转过程中,密度分布 |ψ1,2|2随时间变化,旋转角速率为Ω=0.1Fig.10.Evolution dynamics of the multipolar solitions in the BL with Ω=0.1.

图10(d)给出了np=12 的多极孤立子的旋转过程,可以看出,其旋转过程中保持了很好的完整性,内部各部分之间相对位形保持不变,因此,环状浅势阱中形成的多极孤立子具有良好的稳定性.另外,随着np的增加,稳定的多极孤立子的密度分布在空间形成类似仪表的刻度,能更好地标识旋转运动的角位置,进而根据多极孤立子旋转角速率和坐标系旋转角速率之间的关系,确定坐标系旋转运动的角速率,基于此,有人提出了多极孤立子陀螺的概念[38].

6 结论

BL 势场具有环状势阱和无限深势阱的双重性质,0 阶BL 在势场中央形成类似于抛物型势阱的深势阱,而高阶BL 在第一圆环处可以形成环状浅势阱,这种环状浅势阱由于中央存在势垒,能阻止粒子向中央聚集.BL 势场是非周期性势场,柱对称的BL 势场中央深势阱和第一圆环处的浅势阱更具有特殊性,可以通过势场强度和径向缩放因子分别调节中央深势阱和环状浅势阱的深度和宽度,使得粒子被牢固地束缚在其中形成多种构型的稳态结构.另外,极化激元系统甚至可以在室温下发生相变形成极化激元凝聚,这种能在室温下实现凝聚的系统给量子物理研究带来了十分优越的平台,而在其中通过TE-TM 分裂形成具有较强SOC 作用的双组分旋量极化激元凝聚系统,SOC 作用的引入使得系统多了一个自由度,可以通过调节SOC强度改变系统的稳态结构.

本文把BL 引入具有SOC 作用的双组分旋量极化激元系统,研究了实验室坐标系和旋转坐标系中极化激元凝聚系统的稳态结构.系统的稳态结构包括基础型孤立子(高斯孤立子)、多极孤立子、静态环状孤立子和涡旋环状孤立子.由于多极孤立子在量子导航领域具有潜在应用,本文也验证了多极孤立子的稳定性,在BL 势场的环状浅势阱中形成的多极孤立子具有良好的稳定性,能在旋转坐标系中保持稳定和结构的完整性.