基于虚拟机迁移的能量收集MEC系统资源分配策略

方 鹏，赵宜升，刘志超，陈忠辉

(福州大学 福建省媒体信息智能处理与无线传输重点实验室，福州 350116)

0 引 言

尽管智能移动终端得到快速发展，但计算能力和电池容量仍然相对有限。移动云计算(mobile cloud computing, MCC)技术[1-2]可以将终端的计算任务卸载到云服务器，显著减轻终端的计算压力。移动边缘计算(mobile edge computing, MEC)技术[3-4]是对MCC的补充和优化，可以通过无线接入网络将终端的计算任务卸载到边缘服务器，就近为用户提供计算服务。同时，射频能量收集技术[5]可以从周围环境电磁波中收集能量，为终端持续提供电能。此外，通过设计资源分配策略，能够高效利用收集到的能量。因此，结合MEC的能量收集通信系统的资源分配，能够显著提高系统性能。

结合MEC的能量收集通信系统的资源分配问题已经吸引了较多学者观注文献[6]中移动设备由无线接入点(access point, AP)通过无线功率传输技术进行供电，将计算任务卸载至MEC服务器，在完成用户计算任务的基础上，以最小化AP的总传输能量为目标，提出一种资源分配策略。文献[7]利用收集到的射频能量为MEC系统供电，移动设备使用收集到的能量来进行本地计算或将计算任务卸载给MEC服务器，以最小化本地计算的能量消耗为目标，提出一种动态计算任务卸载策略。文献[8]在一个具有射频能量收集的MEC系统中，采用体现任务执行时延和任务失败的执行成本为性能指标，提出一种基于李雅普诺夫(Lyapunov)结构的低复杂度计算任务卸载算法。文献[9]研究基于MEC服务的多用户联合计算任务卸载和资源分配问题，为了最小化所有移动设备在约束条件下的总任务执行时间，提出一种计算卸载和资源分配算法来动态确定移动设备的能量收集时间，进而提高系统性能。文献[10]考虑用户在移动性场景中具有多频段射频能量收集功能，提出一种基于MEC的异构网络上行资源分配方法，达到最大化能量效率的目标。文献[11]提出基于多阶段随机规划的分布式博弈理论来激励相邻移动设备共享自己的感知资源。然而，现有的大多数研究没有考虑用户移动性对MEC服务器反馈计算结果的影响。当用户移动时，其位置发生改变，和所连接的MEC服务器的距离在不断增大。当用户移动到超出当前基站的覆盖范围时，原来的MEC服务器如何将计算结果及时反馈给用户，是面临的一个挑战。文献[12]提出一种虚拟机(virtual machine, VM)迁移策略，可以对数据通过VM进行迁移。受文献[12]的启发，在用户发生远距离移动时，如果通过VM迁移的方式将MEC服务器的计算结果反馈给用户，可以在很大程度上减小反馈时延。

针对用户远距离移动后对MEC服务器反馈计算结果的影响，本文提出一种基于VM迁移的最大化系统能量效率的资源分配策略。用户在移动过程中，可以从多个频段中收集环境射频能量。当用户移动后，由MEC控制器发起VM迁移，将用户卸载给原始MEC服务器的计算任务迁移到当前MEC服务器。当前MEC服务器处理完计算任务后，将计算结果直接反馈给用户，能够大幅度降低时延。综合考虑用户卸载计算任务和MEC服务器反馈计算结果，将资源分配问题建模为混合整数非线性规划(mixed-integer nonlinear programming, MINLP)问题，以最大化系统能量效率为目标,同时受能量消耗、子载波分配和发射功率的限制。通过引入遗传算法获得该问题的次优解。最后，通过仿真对提出的资源分配策略进行性能评估。

1 系统模型

本节研究系统模型。先给出网络结构，然后分别分析移动模型和能量收集模型。

1.1 网络结构

基于MEC的网络场景如图1所示。MEC服务器部署在用户附近，由MEC控制器分配不同区域用户所连接的服务器。假设有K个用户在该网络中，用户k(k=1,2,…,K)可用一个三元组Tk≜(bk,dk,rk)来表示，bk表示用户卸载给服务器的数据量，dk表示服务器的中央处理器单元(central processing unit, CPU)处理数据所需要的计算量，用CPU周期数来表示，rk表示服务器处理完成后的数据量。每个用户移动前位于位置A，在t1,k时间段，一个基站服务K个用户，用户k将数据量bk通过其附近的基站上传给服务器。待计算任务卸载完成后，用户开始移动，移动的时间为t2,k，移动模型见下一小节。待每个用户移动到各自的位置B后，MEC控制器检测到用户位置发生改变，为用户重新分配新的服务器，并指示初始服务器上对应的VM迁移到新分配服务器上，每个用户均有相关联的基站为其服务，此阶段花费的时间为t3。新分配服务器处理用户上传的计算任务所消耗的时间为t4,k。在t5,k时段，新分配服务器将处理后的数据rk通过基站传给用户。

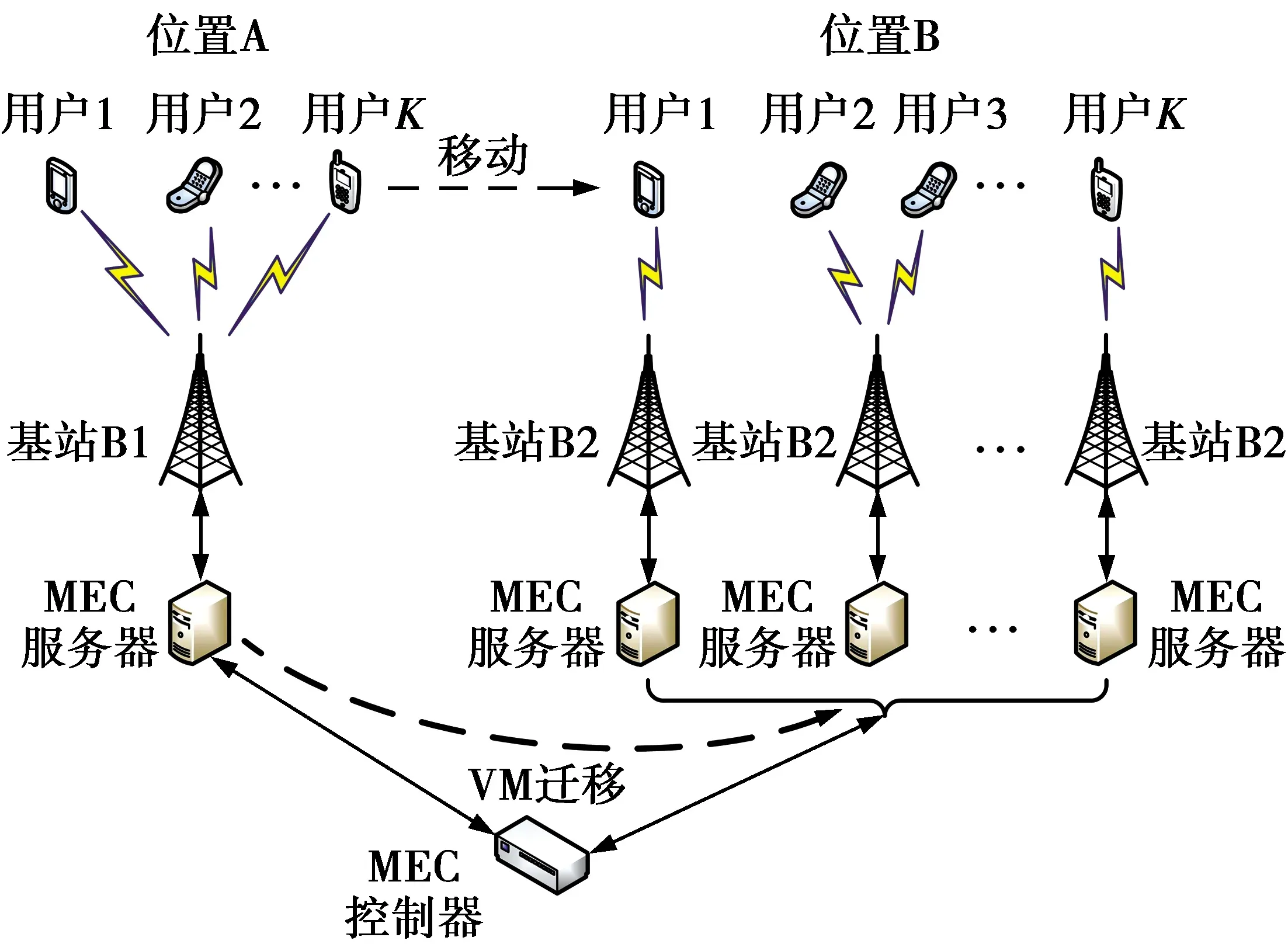
图1 基于移动边缘计算的网络场景Fig.1 Networks scenario based on mobile edge computing

1.2 移动模型

本小节分析用户移动模型。建立一个以米(m)为单位的直角坐标系，假设用户k的初始位置表示为(xk(0),yk(0))，每个用户在随机方向上沿直线移动，移动方向通过角度来表示。用户移动速度为v，经过时间Tstep后，每个用户随机改变其方向并继续沿直线移动，一共改变Qk次方向。用户k在t时刻的位置表示为(xk(t),yk(t))。具体的移动模型可以表示为

(1a)

(1b)

(1a)—(1b)式中：q表示用户改变移动方向的次数；角度θ0和θq都为在[-π,π]均匀分布的随机数。

1.3 能量收集模型

本小节分析用户能量收集模型。每个用户均配备宽带天线，可以不间断地从以下5个频段[13]的环境射频源中收集能量：数字电视，频段为550～600 MHz；LTE，频段为750～800 MHz；GSM900，频段为850～910 MHz；GSM1800，频段为1 850～1 900 MHz；UMTS，频段为2 150～2 200 MHz。相应的发射机是电视塔和不同类型的基站。

假设用户周围共有L个发射机，并且发射机均在持续地发射电磁波。根据文献[14]，可得到用户k在时间段t内收集到的射频能量为

(2)

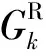
(3)

2 资源分配问题建模和求解

本节提出具体的资源分配策略。首先，建立资源分配最优化问题模型。然后，通过引入遗传算法，来对优化问题进行求解。

2.1 问题建模

针对第1小节的系统模型，提出一种系统能量效率最大化的资源分配策略。假设用户移动前所对应的基站为B1。在t1,k时间段，用户k对基站B1的上行吞吐量为

(4)

(5)

用户k所消耗的能量表示为

(6)

基站B1和所有用户在该时间段所消耗的总能量分别表示为

(7a)

(7b)

在t2,k时间段，用户从位置A移动到位置B，移动了Qk次，则

t2,k=QkTstep

(8)

用户的电路能量消耗为

(9)

假设所有用户对应的服务器移动前为A，移动后为B。在t3时间段，服务器A向各个服务器B发起VM迁移，VM的大小为BVM，假设迁移一台VM所消耗的能量为σ，则所有用户对应的服务器迁移VM所消耗的能量为

EVM=Kσ

(10)

用户的电路能量消耗为

(11)

在t4,k时间段，服务器B计算用户上传的数据bk。所需要的计算量dk=αbk，α为服务器计算每bit数据所需要的CPU周期数，则服务器B完成计算量所花费的时间与消耗的能量分别为

(12a)

(12b)

(12a)—(12b)式中：f为服务器所能提供的计算能力；ε为每个CPU周期的能量消耗。用户的电路能量消耗为

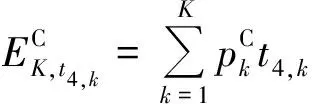
(13)

(14)

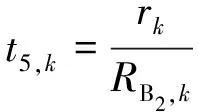
(15)

用户k接收数据所消耗的能量为

(16)

(17a)

(17b)

因此，系统所传输的总数据量为

(18)

系统所产生的能量消耗为

(19)

将功率和子载波分配问题建模为最优化问题。优化目标是最大化系统能量效率[15-16]，同时满足若干约束条件。该优化问题模型可表示为

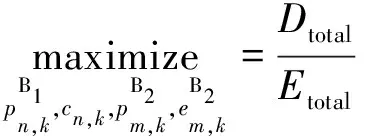
(20a)

(20b)

(20c)

cn,k∈{0,1},∀n,k

(20d)

(20e)

(20f)

(20g)

(20h)

(20i)

(21)

2.2 遗传算法优化

MINLP问题具有较高的复杂度，直接求解复杂度极高，可以使用启发式算法进行次优求解。根据文献[17-18]，遗传算法是一种借鉴生物界自然选择和自然遗传机制的随机搜索算法，适用于求解复杂的优化问题。该方法具有一定的随机性，可以逐代演化产生出越来越好的近似解。图2为基于遗传算法的资源优化策略流程图。

图2 基于遗传算法的资源优化策略流程图Fig.2 Flow chart of resource optimization strategy based on genetic algorithm

首先，产生初始种群。假设种群中个体数量为P，并将K个用户的子载波分配因子和发射功率定义为个体的染色体，则个体p(p=1,2,…,P)的染色体向量可以表示为

(22)

(23)

本文采用实数编码，通过随机方式产生所有个体染色体的初始值。

其次，计算适应度值。适应度值表示个体对环境的适应程度，用于区分个体的优劣。适应度值越大，个体越优秀。根据文献[19]，通过惩罚函数法将(20b)—(20i)式所示的约束优化问题转化成无约束形式，构造一个由目标函数和惩罚函数组成的适应度函数，形式如下

(24)

(25)

包含8项，分别对应公式(20b)—(20i)的8个00约束条件，具体形式为

(26a)

(26b)

(26b)

(26d)

(26e)

(26f)

(26g)

(26h)

(26a)—(26b)式中，max(·,·)表示在两个数值之间取较大的一个数值。对于(26a)式的C1和(26b)式的C2，分别表示为

(27a)

(27b)

根据构造好的适应度值函数，代入每个个体的染色体，分别计算适应度值。惩罚函数法是从解的非可行域出发逐渐移动到可行域的方法。如果当前种群为可行解，则fpen=0，从而有F=fobj；如果当前种群个体为非法解，则γfpen为较大的正数，它的存在是对该个体脱离可行域的一种惩罚，其作用是在极大化过程中迫使解靠近可行域。

最后，判断是否达到终止条件，得到次优解。如果达到最大迭代次数，从所有适应度值中选出一个最大的，其对应个体的染色体为次优解。否则，进行遗传操作。遗传操作是仿照达尔文进化论对染色体的基本操作，分为选择、交叉和变异。选择是根据适应度值大小对种群个体进行优胜劣汰操作，采用轮盘赌选择法[20]对种群进行选择，个体的适应度值越高，被选入下一代的概率就越大；交叉采用单点交叉法使得两个配对的染色体在其交叉点处相互交换其部分染色体，从而形成两个新的个体；变异是以较小概率对个体上某个或某些位的值进行改变，决定了遗传算法的局部搜索能力。本文使用均匀变异法和高斯变异法[21]协作，使得遗传算法能够以良好的搜索性能完成寻优过程。经过遗传操作以后，产生新的种群。根据适应度函数，计算新种群中所有个体的适应度值。直到达到终止条件，得到次优解。

3 仿真结果与分析

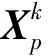
图3对比了不同惩罚因子下三种策略的能量效率。在仿真中，遗传算法中的种群数量和迭代次数都设置为200，用户数量K=5，子载波数量N=M=60，VM大小BVM=800 MB。从图3中可以看出，能量效率随着惩罚因子的增加逐渐降低。这是因为惩罚因子的大小决定着算法对非法解的惩罚大小。当惩罚因子取值大于1.5时，能量效率下降的速度加快。因此，在接下来的仿真中，将惩罚因子设置为1.5。

图4评估了遗传算法中种群数量和迭代次数对能量效率的影响。在仿真中，用户数量K=5，VM大小为BVM=800 MB，子载波数量N=M=60。从图4中可以看出，随着种群数量和迭代次数的增大，能量效率也随之增大，并逐渐趋于平稳。这是因为种群数量和迭代次数的增多可以使得算法的全局搜索性能增加，但效果最终也会趋于饱和。此外，能量效率的大小存在不同程度的波动，当种群数量为160，迭代次数为160时，能量效率达到最大。因为遗传算法中存在变异算子，使得最佳适应度值具有一定的随机性，但这并不影响算法趋于收敛的趋势。在接下来的仿真中，将种群数量和迭代次数分别设置为160和160。

图3 惩罚因子和能量效率的关系Fig.3 Relationship between penalty factor and energy efficiency

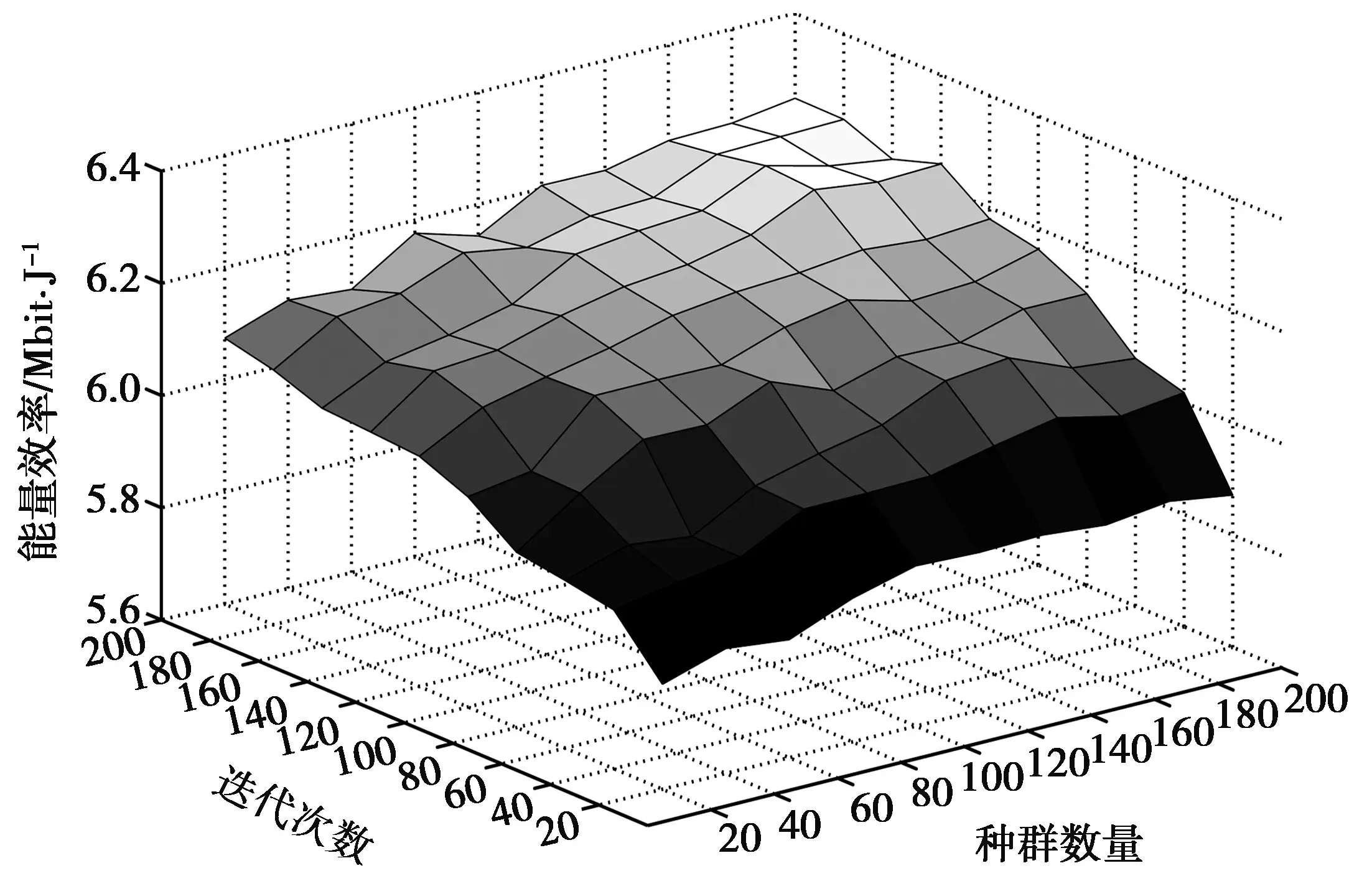
图4 遗传算法中种群数量和迭代次数对能量效率 的影响Fig.4 Effect of population size and iteration times on energy efficiency in genetic algorithm

图5对比了不同VM大小下四种策略的能量效率。在仿真中，用户数量K=5，子载波数量N=M=60。在文献[24]的基础上，当网络带宽为100 Mbit/s时，根据800 MB、1 800 MB和2 700 MB三种VM大小对应的迁移能耗和迁移时长，得到表1。从图5可以看出，随着VM的增大，四种策略的能量效率均随之变大。这是因为VM的大小影响着系统的总数据量以及总能耗，但总数据量要比总能耗增长得快。此外，提出方法的优化能力要比其他三种方法好，P-GA的优化能力与提出方法相近，并且高于S-GA和EP-HS。这是因为发射功率对能量效率的影响比子载波分配因子更为显著。

表1 不同VM的参数Tab.1 Parameters of different VMs

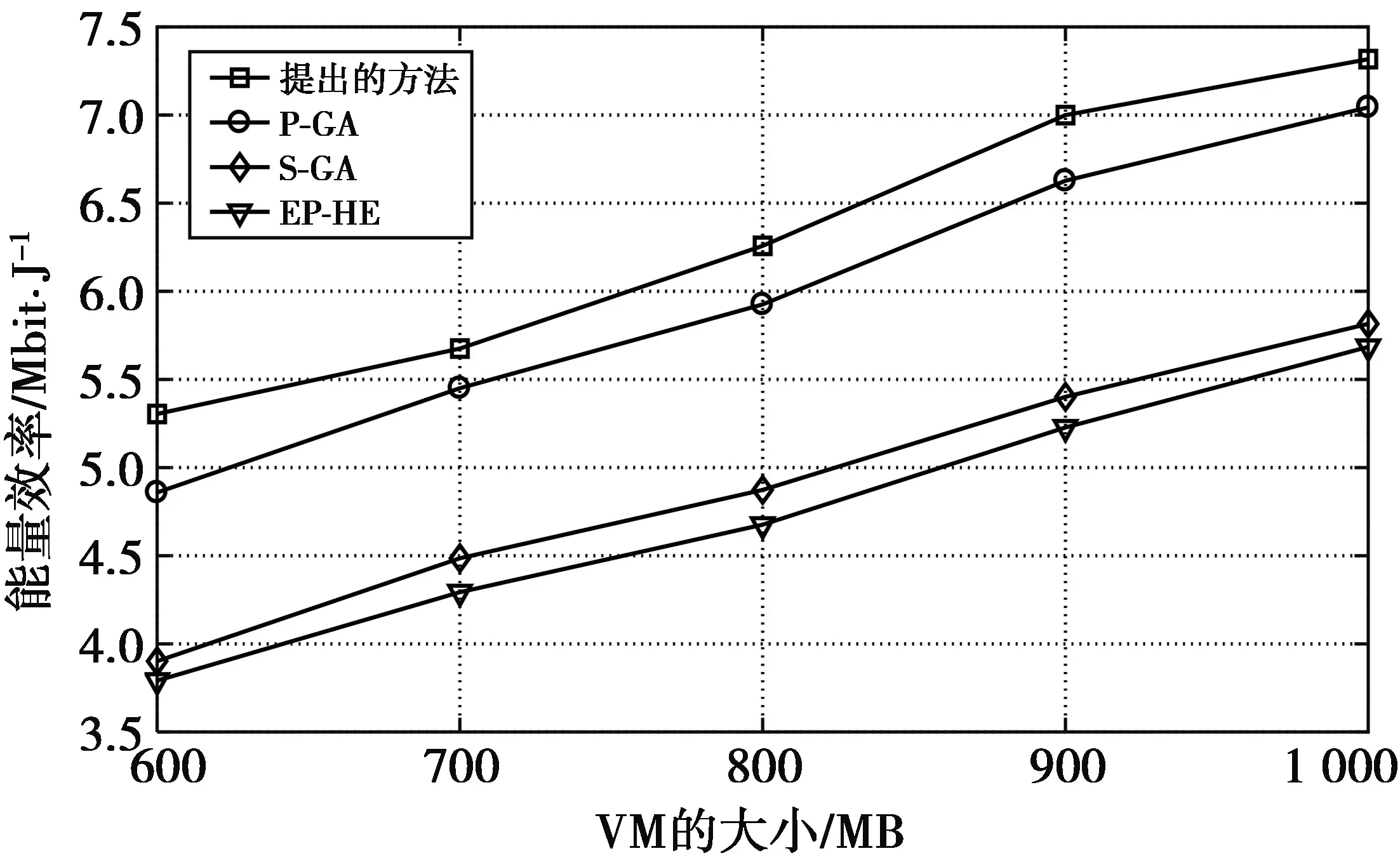
图5 VM大小和能量效率的关系Fig.5 Relationship between virtual machine size and energy efficiency

图6对比了不同用户数量下四种策略的能量效率。在仿真中，VM大小BVM=800 MB，子载波数量N=M=60。从图6可以看出，在不同的用户数量下，提出方法比其他方法具有更高的能量效率。这是因为提出方法同时对发射功率和子载波分配因子进行搜索，具有更好的优化能力。此外，对于提出的方法和P-GA，随着用户数量的增加，能量效率明显降低。这是因为系统总能量消耗的增长速度高于总数据量。

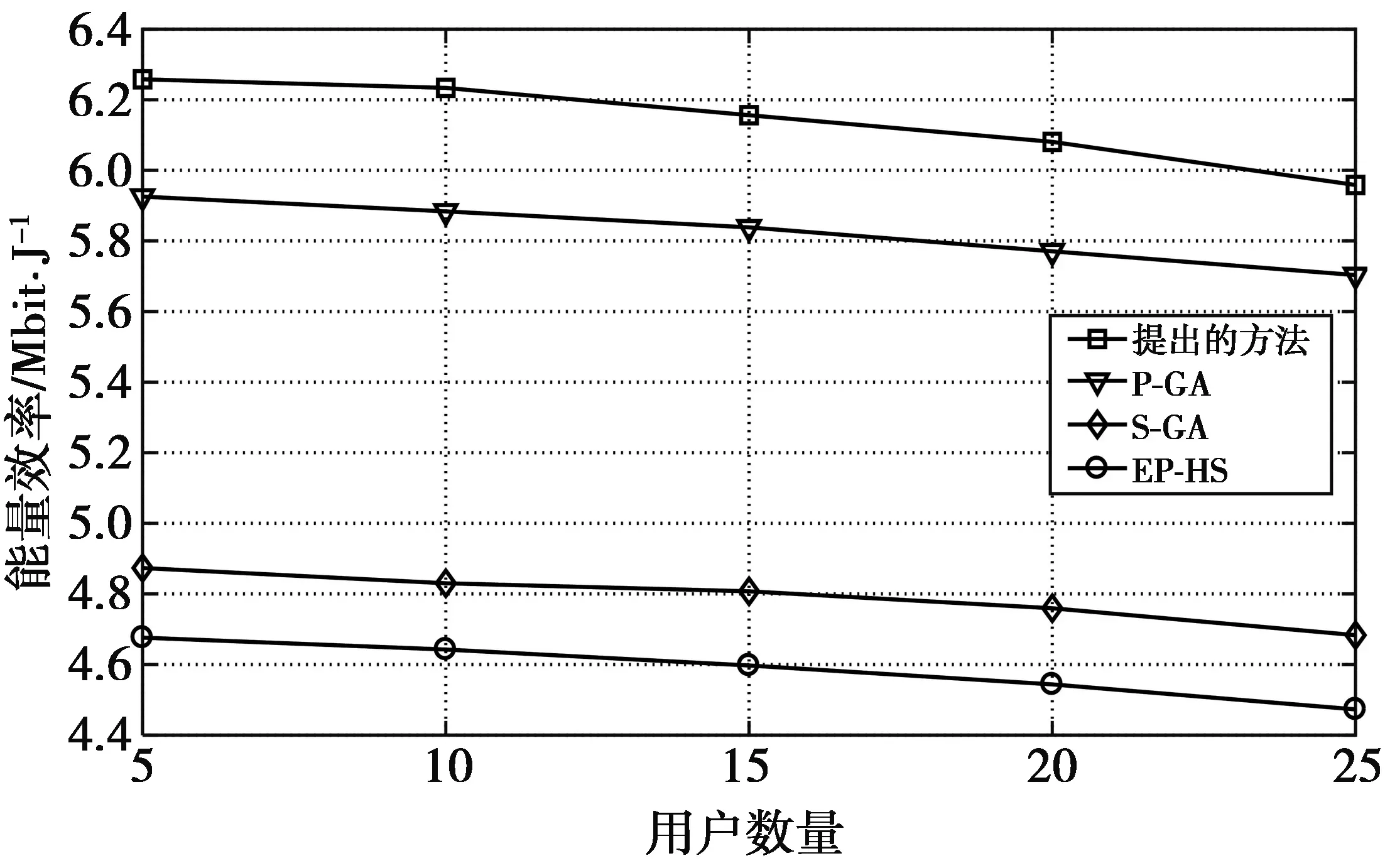
图6 用户数量和能量效率的关系Fig.6 Relationship between number of users and energy efficiency

图7对比了不同子载波数量下四种策略的能量效率。在仿真中，用户数量K=5，VM大小BVM=800 MB。从图7可以看出，当子载波数量从50到100逐渐增大时，能量效率也逐渐变大。这是因为数据传输的速度随着子载波数量的增多而增大，导致系统总的电路能量消耗变小。此外，提出方法和P-GA的优化能力明显比S-GA和EP-HS强，具体原因同图5所述。

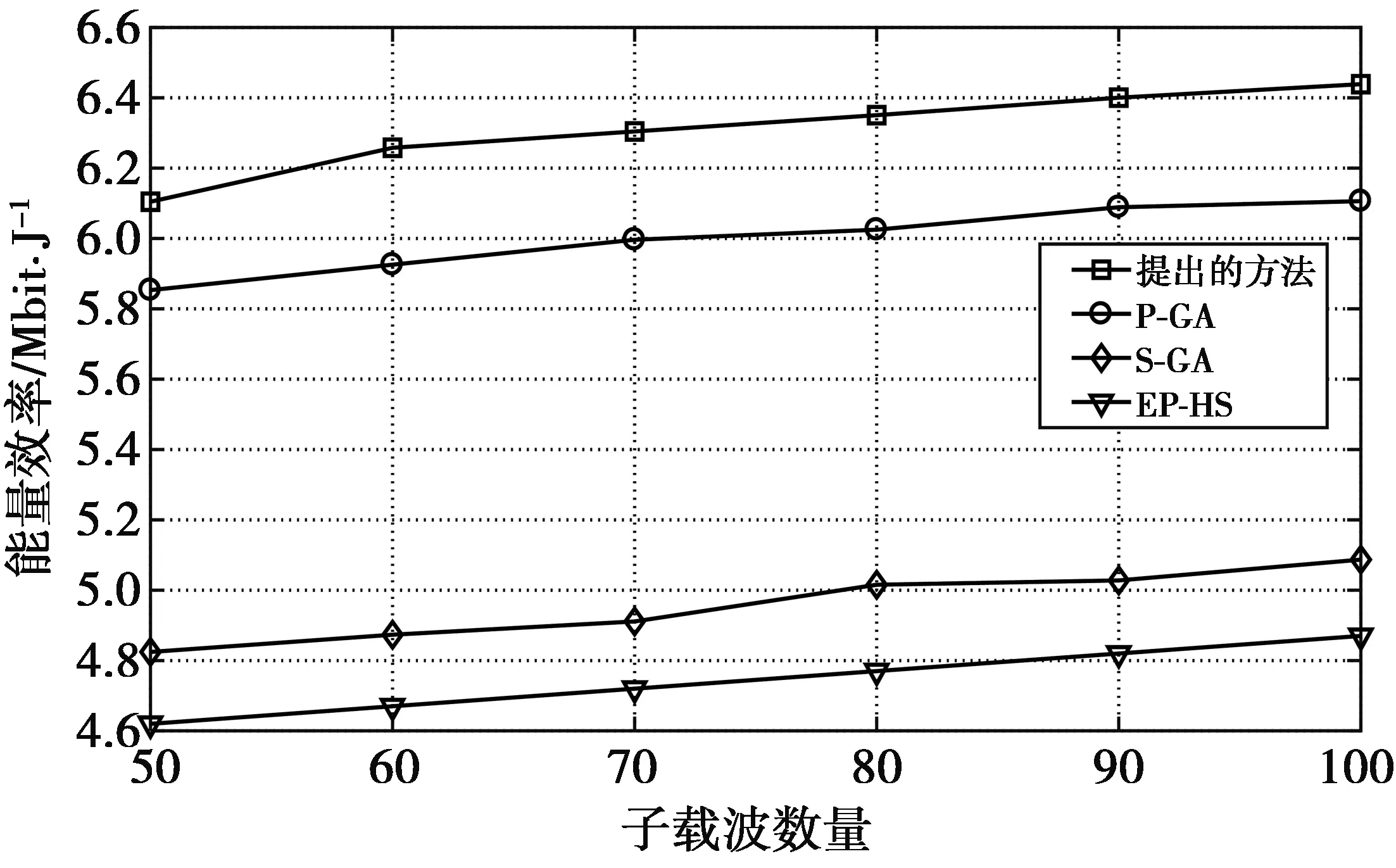
图7 子载波数量和能量效率的关系Fig.7 Relationship between number of subcarriers and energy efficiency

4 结 论

本文针对用户移动性对MEC服务器反馈计算结果的影响，提出一种基于VM迁移的最大化系统能量效率的资源分配策略。用户在移动过程中，能从多个频段收集环境射频能量。当用户远距离移动时，采用VM迁移的方式，把用户卸载给初始MEC服务器的计算任务转移到当前MEC服务器。当前MEC服务器完成计算任务以后，将计算结果直接反馈给用户，能够显著降低时延。联合考虑用户卸载计算任务和MEC服务器反馈计算结果，将资源分配问题建模为MINLP，在满足能量消耗、子载波分配和发射功率的约束条件下，以最大化系统能量效率为目标。通过引入遗传算法进行求解，获得次优解。仿真结果显示，与S-GA、P-GA和EP-HS方法相比，提出的方法具有更高的能量效率。本文假设用户在卸载完计算任务后才开始移动，未来的工作中，将考虑用户在卸载部分计算任务时就开始移动的情况，并针对用户对服务连续性要求较高的实时性业务，采用实时虚拟机迁移的方式，开展进一步研究。