CSMA/CA网络协议的无线区块链安全性研究
朱晓明,刘 蓓,白 翔,李孟阳
(1.中国电子科技集团公司第五十四研究所,石家庄 050081;2.中国电子科技网络信息安全有限公司,成都 610041;3.重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
在现今的网络数据存储中,关系型数据库管理系统和NoSQL数据库应用都是由专业的软件服务商开发的,而数据库管理人员对数据库的数据拥有绝对的控制权,公众无法判别数据的真实性和参与数据的更新进程[1]。不仅如此,每个商业公司的数据库都是“集中式的”,因为它的管理权和维护权都被商业公司唯一享有。另一方面,集中式数据库容易成为信息孤岛,它极大地提高了信任的成本,同时阻碍了共享经济的发展。比特币[2]的出现将其去中心化的分布式账本技术带入人们的视野,为新一代互联网架构的改革方向提供了思路。
众所周知,区块链是电子数字货币系统稳定运行的基础[3]。区块链集成了P2P协议、哈希计算、数字签名、非对称加密和共识算法等多种技术,一方面保障了数据的安全性;另一方面解决了数据的信任问题[4]。然而,现有区块链平台的性能和安全还远不能满足人类社会的生产需求。相应地,当前区块链的理论研究主要是考虑共识算法层面的优化和安全问题,还没有研究从通信的角度去考虑区块链的共识算法和安全问题。
区块链是共识算法、密码学和通信网络3种核心技术的结合体,而通信网络是区块链的交易过程的基础设施。具体而言,网络中的参与节点贡献自己的资源,比如网络传输资源、计算资源、数据存储资源等。所有节点在网络中的拓扑连接都是扁平化的,这意味着整个网络中没有特殊的节点,任何节点都是资源的提供者和使用者。从通信网络的角度来看,区块链是一个对通信质量要求极高且容易敏感的技术,如果区块链的通信环境非常恶劣,那整个区块链的共识进程一定会遭受阻碍。另外,通信协议是通信网络的必不可少的部分,但是区块链对通信协议种类没有任何的限制[5]。因此,共识算法在与通信场景的匹配上也存在许多亟待解决的问题。比如,移动自组网下的特点是无中心、多级中继,动态路由和抗毁能力强的网络,主要用于军事、应急安全等场景[6]。那么,研究人员需要考虑区块链中哪种共识算法能够与通信协议相匹配,从而发挥较好的性能。
另一方面,安全性是区块链系统能否正常运转的基本保证,它主要分为通信安全和共识安全。对于通信安全而言,网络数据监听和篡改是区块链面临的首要威胁。在比特币系统中,区块链技术增加了流量加密协议来避免P2P通信的监听。不仅如此,在网络层引入智能路由链路的流量监测,检测行为不正常的节点以避免自己受到攻击。因此,对于不同的区块链系统,它的安全级别是否满足应用的条件是学术界和工业界首要考虑的问题[7]。
共识算法是区块链共识安全的体现。而非安全共识会导致交易或区块(比如比特币中的数字货币)的双重花费[8-10],即同一个数字货币可以获得2次及以上商品或服务。从通信系统的角度来看,双重花费可以理解为恶意节点欺骗了其他的诚实节点。在缺少了中心化的权威机构后,区块链中没有公认的实体去验证每笔数字交易的合法性。为了应对双花问题,区块链系统改进共识算法,让节点花费更多的计算资源和电力成本来保证账本的真实性。同时,区块链系统还引入了验证交易的激励机制,加快了交易的验证速度,从而大大增加了攻击者的成本[11]。
基于此,本文专注于研究共识算法能否完美地匹配特定通信场景下的网络协议,通过建立数学模型,针对具体的共识算法,定量地分析特定通信场景下区块链的双花安全。详细地说,本文着重探讨在接入控制协议的影响下攻击者发起双花攻击的攻击进程,从而得到双花攻击成功概率的变化情况。该研究针对无线通信场景中的区块链安全问题,从通信层面指出了要想提高区块链的安全性必须要考虑适配的通信协议,对未来的区块链研究具有理论和指导意义。
1 预备知识和相关工作
共识算法的核心作用是在互不信任的节点之间提供一份统一的账本。区块链中常见的共识算法有工作量证明(proof of work, PoW)[12]、权益证明(proof of stake,POS)[13]、基于有向无环图(directed acyclic graph,DAG)的共识算法[14]、实用拜占庭容错(practical Byzantine fault tolerance,PBFT)[15]等。下面将详细介绍本文采用的基于DAG的共识算法和载波多路侦听/碰撞避免(carrier sense multiple access/collision avoidance, CSMA/CA)通信协议[16]。
1.1 预备知识
1.1.1 共识算法
在基于DAG结构的共识算法中,研究和应用最广泛的算法是Tangle共识[17],Tangle账本结构如图1。其中,任何2笔交易之间相连接的边表示节点在接入区块链时验证了哪些旧交易。那么,直接相连的边代表着两交易的直接验证,间接相连的边代表着两交易的间接验证,例如,图1中H直接验证了C,而I间接验证了E。图1中数字表示每个交易的2个参数:①累积权重;②自身权重。另外,交易的自身权重与交易加入到区块链中花费的工作量证明有关,而累积权重是该交易的自重再加上所有直接或者间接验证该交易的累积权重之和。因此,一个交易的累积权重越大,代表着它在账本中存在的时间越长,就越难被篡改。交易的累积权重的大小直接影响着交易在区块链中是否被验证,这与系统所设定的验证阈值有着紧密的关系。值得注意的是,系统验证阈值的设定间接决定了Tangle共识的速度和账本的安全性。另外,图1中的Tip表示账本中还未被新交易选择的一类交易集合。
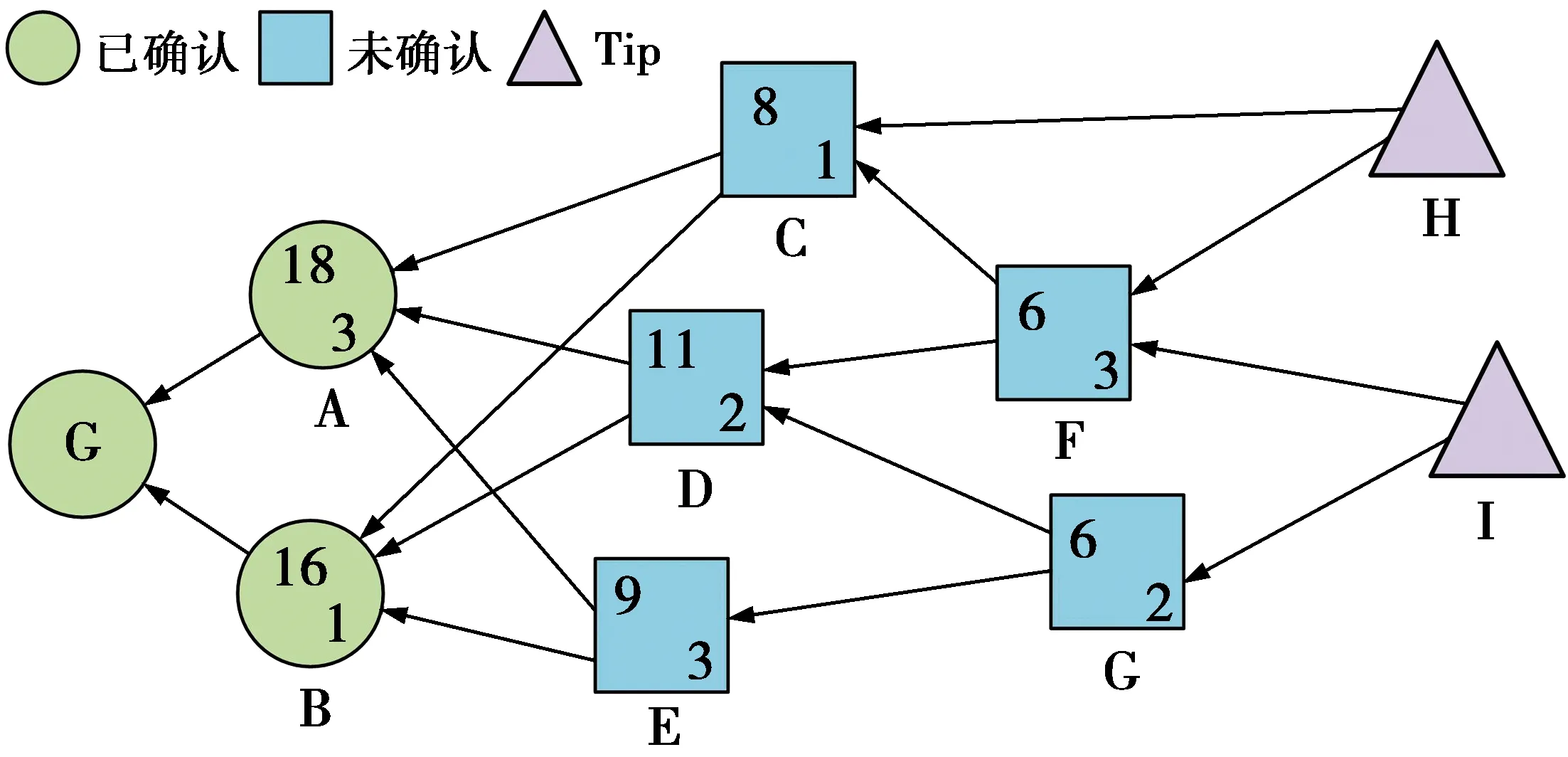
图1 Tangle账本结构图Fig.1 Typical structure of tangle
在Tangle共识,节点在选择旧交易是遵循马尔可夫链蒙特卡罗(Markov chain Monte Carlo, MCMC)算法的。该算法背景是随机概率中经典的随机游走理论,节点在特定区间的权重值上随机游走,多次试验后,节点总是倾向于选择权重值更大的交易,并且最后在随机游走次数较多的位置停下。在Tangle共识中,发现节点这一行为能够有效提高账本的安全性。
1.1.2 通信协议
绝多数无线网络场景使用的协议标准都是IEEE 802.11协议簇,其中媒体控制接入访问机制通常采用分布式协调一致功能(distributed coordination function, DCF)[18],它是一种基于CSMA/CA协议来随机接入节点的工作模式。在本文中,本文假定任何节点需要遵循CSMA/CA协议的规则,通过竞争无线信道来广播数据交易到无线区块链网络(wireless blockchain network, WBN)中。
DCF机制在传输数据包时采用四次握手的过程如图2。在广播数据交易之前,发送方节点需要监听信道的状态是否为空闲。如果信道空闲,发送方节点和接收方节点依次发布请求发送指令(request-to-send, RTS)、清除发送指令(clear-to-send, CTS)、数据交易和接收确认指令(ACK),而网络中其他的节点需要更新自己网络分配向量状态器来记录当前信道状态是繁忙的。如果信道不是空闲的,发送方节点需要等待一个退避时间来准备下一次的数据传输。需要注意的是退避时间其实是一个计数器,它是从当前竞争窗口(contention window, CW)区间以均匀分布随机选取一个数值来作为当前退避时间。在每次数据交易传输时,如果出现了传输失败,那么竞争窗的大小会增大一倍,以降低节点在传输数据交易时发生碰撞的概率。在不同网络协议标准中,CW的最大值和最小值各不相同,通常有CWmax=2SCWmin,S表示当前网络采用最大退避次数。
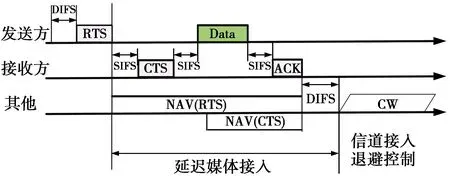
图2 基于DCF机制的CSMA/CA协议流程图Fig.2 Communication process of DCF based CSMA/CA
1.2 相关工作
当前,已有学者提出了许多有潜力的业务解决方案和架构来探究区块链的安全性。在车辆自组网(vehicular ad hoc networks, VANETs)领域,文献[19]提出了一种车载单元根据道路基础单元共同组建移动自组网的架构。该架构将车—车通信与车-基础设施通信结合到一起,解决了车联网通信的信息安全和隐私问题,并使得车辆行驶中信息传输通信的时延降到更低。在设备与设备(device to device, D2D)通信领域,文献[20]设立一系列接入点(access points, APs)来验证终端节点的交易,构建了安全的分布式的数据分享D2D区块链架构。它提出了协助中级交易的转发方案,并探讨最优的区块价值和交易价值来激励含有丰富资源的节点与转发交易,实现了一种高效且安全的数据D2D通信的数据分享解决方案。更有甚者,文献[21]提出区块链通信网络(blockchain communication network, BCN)的概念,在OSI体系中增加一层用来区分网络数据流类型,将区块链数据流和一般数据流分别传输交付到网络层,根本上解决现有区块链效率偏低的缺点。文献[22]在比特币双花攻击模型基础之上,使用正则化的Beta函数来推导出双花攻击概率的闭合表达式,同时给出了攻击概率随着区块确认数量增加而指数型下降的证明过程,最后,还提出渐进公式来逼近攻击概率的变化。文献[23]搭建NS-3的网络仿真平台来模拟比特币中攻击者的行为,结果表明,攻击者增大攻击成本和攻击次数会严重威胁到区块链系统的安全。此外,文献[24]提出一种基于区块链技术保护NFC移动支付安全的解决方案,它将区块链技术集成到支付设备从而实现支付场景的隐私和安全保障。
2 系统模型
2.1 攻击模型
根据文献[25],恶意节点通过秘密地构建寄生链发动双花攻击。寄生链攻击示意图如图3,本文中攻击者发动双花攻击的具体过程如下。

图3 寄生链攻击示意图Fig.3 Parasite chain for double-spending attack
1)在t0时刻,攻击者广播一笔真实付款交易给商家,Tangle共识网络中的其他节点开始选择此交易来批准。
2)在t1时刻,攻击者以离线的方式构建寄生链来批准已经准备好的与真实付款相冲突的交易(也称为双花交易),并且它只在本地账本中秘密地附到账本中Tip。注意,t1时刻也是真实付款交易适应期子阶段结束的时间。
3)在t2时刻,真实付款交易的累积权重到达了系统认证阈值ω。然后,商家发送产品或服务给攻击者。
4)在t1时刻之后,攻击者不断消耗自己的算力来发布许多毫无意义的交易去增加双花交易的累积权重。
5)在t2时刻之后,只要双花交易的累积权重超过了真实付款交易的累积权重,攻击者可以广播它的寄生链到WBN中。
6)攻击者在成功竞争到无线信道后,一次性将寄生链更新到整个Tangle共识网络中。由于寄生链分支在系统中有者更高的累积权重,WBN中其他诚实节点根据MCMC选择算法将会批准双花交易。因此,账本中真实付款交易将会被Tangle共识网络孤立,商家将无法获得相应的报酬。最终,攻击者成功地实现了双花攻击。
2.2 问题抽象
假定WBN中有n-1个节点和1个攻击者来参与Tangle共识,节点之间在相同信道下互相通信交换信息。每个节点的交易到达率假定服从泊松分布,用λ表示诚实节点节点的交易到达率,用μ表示攻击者的新交易到达率。为了方便研究交易的累积权重增长变化,将每个交易的自重都归一化处理设为1。
在WBN的无线通信中,节点按照CSMA/CA协议获得信道后成功传输一个数据包花费的平均传输时延设为h,它也是相邻的2次广播之间的时间间隔。根据DCF机制的数据传输方式和无线网络的参数设置,可以准确地计算出信道的平均传输时延h。此外,无线信道的容量资源是有限的,假定最大容量是l笔交易,那么每个节点受到其限制也只能一次向无线信道中广播l笔交易。与此同时,h也是Tangle共识中节点发布一个新交易的揭示时间。
考虑到WBN网络流量负载的影响,本文将模型划分为低流量负载和高流量负载2种场景来描述不同队列缓存状况。
2.2.1 低流量负载场景
当网络流量为低负载时,用λ=λl表示该网络场景。根据CSMA/CA协议的DCF机制,每个节点获得信道权的机会是均等的,均为1/n。那么,节点在上一轮使用无线信道后想要重新成功竞争到无线信道的平均等待时间是nh,该节点的队列缓存中累计的待广播交易数量是nhλl。当nhλl小于等于一次广播的最大容量l个交易时(即nhλl≤l),节点在竞争到无线信道后,本地缓存的所有交易都能够一次性地通过无线信道广播到WBN中参与共识。
2.2.2 高流量负载场景
当网络流量为高负载时,用λ=λh表示该网络场景。与之相对,网络流量与无线信道大小的关系为nhλl>l。在这种情况下,即使节点当前享有信道权,也无法将队列缓存中的所有交易一次性全部广播到无线信道里,并且广播成功后,队列缓存的剩余交易需要继续等待下一次广播。此外,如果网络流量特别大,队列缓存空间被填满,后续到达的新交易将被丢弃。需要注意的是,因为无线信道的容量上限是l个交易,那么每一轮广播新进入Tangle共识中交易最多只有l个。
接下来,本文利用马尔可夫链模型来抽象双花攻击的过程。在t1-t2时刻,假定诚实节点和攻击者发布的双花交易数量分别为ih和ia。诚实节点与攻击者发布交易竞争的状态流如图4,每个马尔可夫状态定义为诚实节点与攻击者发布交易数量的差值,同时这里的初始状态是t2时刻下的差值ih-ia。更详细地说,状态“+1”和“-1”表示Tangle共识网络中的下一个交易是攻击者发布的还是诚实节点发布的。

图4 诚实节点与攻击者发布交易竞争的状态流图Fig.4 State flow for transactions issuing competition between attacker and honest nodes
根据以上分析,双花攻击成功的概率为
P{攻击成功}=P{时刻t2攻击成功}+
{1-P{时刻t2攻击成功}}P{时刻
t2之后攻击成功}
(1)
需要注意的是,攻击者不能在t2时刻之前广播寄生链到WBN中,因为此时真实付款交易还未被区块链验证。也就是说,攻击者发动双花攻击一定在攻击条件满足后的t2时刻之后进行。
3 理论分析
3.1 理想通信下的双花攻击
为了简洁形象表示攻击过程,本文定义状态“0”为攻击者发布的交易还没有超过诚实节点发布的交易,状态“1”表示攻击者赢得了双花攻击。那么,图4转化为一步概率转移图,如图5。

图5 理想通信下的一步概率转移图Fig.5 One step state transition probability in expected situation
令Tangle共识网络中下一个到达的交易是诚实节点发布的概率为p,可以表示为
(2)
同理,下一个到达的交易是攻击者发布的概率q,可以表示为
(3)
由随机试验的特点,攻击者竞争过程可以视为独立重复的伯努利试验。在t2时刻,当攻击者发布的交易数量超过了诚实节点发布的数量,攻击者可以选择广播它的寄生链。否则,攻击者必须继续消耗算力发布交易来增加累积权重。因此,攻击者在t1-t2时刻发布的交易数量α是一个随机过程。依据文献[26],攻击进程函数α的概率密度是可以写成
(4)
(4)式中,Tq,ia表示攻击者控制的算力为q,同时发布了交易数量为ia所花费的时间。因为每个交易间是互不关联的,且攻击者的交易到达率服从泊松分布,那么交易的揭示时间间隔服从指数分布。换句话说,攻击者在时间Tq,ia内相当于做了ia次指数分布的独立试验,从而Tq,ia是服从整数变量的伽马分布。根据随机理论,可以写出其概率密度函数为
(5)
根据概率分布与概率密度函数之间的关系,对(5)式积分可以得到攻击者在t2时刻下,处于状态“0”和“1”的概率表达式分别为
(6)
(7)
如果ia>ih,双花攻击在t2时刻就成功了。否则,攻击者必须继续追赶诚实节点所更新的账本分支,并且不断地发布交易来弥补二者之间的差距。在t2时刻之后,攻击者的寄生链分支累积权重一旦超过了当前主分支的累积权重,追赶就成功了。然而,攻击者可以提前以离线的方式构建寄生链,一旦双花攻击开始发动了,攻击者的追赶进程也就开始了。那么当双花攻击还未开始时,即t<0,追赶概率也就不存在。最重要的是当双花攻击成功时,Tangle共识网络中最近新进入的交易一定是由攻击者发布的。那么,相应的追赶概率可以表示为
(8)
在t1时刻,真实付款交易已经获得批准,它的交易数量为W(t1)-1。因此,在t2时刻,真实付款交易也应被系统验证,它需要获得的由诚实节点发布的交易数量为ih-(W(t1)-1)。同理,Tangle共识网络中诚实节点控制的算力为p,发布了ih个交易所花的时间记为Tp,ih。攻击节点不断创建交易过程的概率密度函数为以随机变量XT=Tq,ia-Tp,ih的卷积积分,可以写为
PXT(q,ia,ih,t)=hq,ia*hp,ih=
(9)
最终,由(1)式,可以得到双花攻击成功的概率表达式为
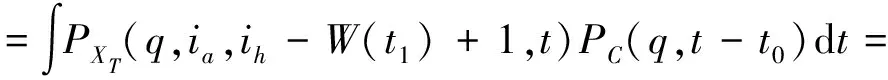
(10)
3.2 CSMA/CA协议下的双花攻击
很显然,CSMA/CA协议对双花攻击的影响主要在进入区块链的交易数量上。当诚实节点和攻击者所发布的交易都被限制,整个系统的双花攻击成功率如何变化值得深究。

(11)
同样,Tangle共识网络中下一个到达的交易是诚实节点发布的概率为p′,可以表示为
(12)
同理,下一个到达的交易是攻击者发布的概率q′,可以表示为
(13)
根据第3节的内容,CSMA/CA协议中初始退避窗口大小为CWmin,最大退避次数是S。那么Tangle共识网络中在排队完成后可能处在的状态有3种:请求发布、成功传输以及失败传输。为了更方便地求出不同状态下的稳态分布,图6用马尔可夫状态转移图来描述攻击者交易在CSMA/CA协议下的切换流程。
基于此,在每个时隙内成功广播数据的概率是ps,交易处在等待请求发布、成功传输和失败传输(碰撞、丢包)的3种状态分别记为Aj、B和Cj。因为交易成功发布后就状态终止,那么这里B是一个吸收态。用状态{Y(t),X(t)}表示交易在t时刻传输更新的状态和传播时候的状态,可以得到一步转移概率为
(14)
(14)式中,Aj,B和Cj分别表示交易在第j次传输的状态为等待请求发布、成功传输和失败传输,j=0,1,…,S。

图6 CSMA/CA协议下的概率转移图Fig.6 State transition probability in CSMA/CA situation
排队完成后的交易处在请求发布状态A0,如果在无线信道中成功传输,它转化马尔可夫图中状态B。否则,在退避区间中设置了退避计数器后,转化为状态Cj,最终进行退避倒计时,回到状态Aj。根据马尔可夫链的一步转移概率性质,可以得到
(15)
由(15)式可得到
(16)
以此类推,得到交易第j次请求发布和传输失败的稳态分布πCj表示为
πCj=(1-ps)πAj,j=0,…,S
(17)
在DCF机制中的二进制退避规则下,由于交易传输失败,其导致交易重发所花费的多余时间记为Dj,那么根据交易是否在一个时隙内发布成功的概率,得到Dj的表达式为
(18)
(18)式中,j=0,…,S-1,而j=S需要重写为
(19)
那么,可以通过计算Dj概率母函数的方法求得它的平均退避时间。令ZDj(z)表示Dj的概率母函数,那么(18),(19)式可以写为
(20)
(20)式中,GDj(z)是几何分布的随机函数,利用迭代递归得到ZDj(z)的一次导数。
当退避次数太多时,攻击者为了提供攻击效率,将直接丢弃该交易重新发布新交易来增加寄生链的累积权重。那么,这里可以用一次退避来代表单个交易由于传输失败所需要多花的平均时间,即
(21)
再结合(10)式,可以得出该种场景下的双花攻击概率为

(22)

4 实验仿真
为了验证CSMA/CA协议对双花攻击可能会产生的影响,本文利用MATLAB设计了多组仿真实验来验证相应的双花攻击概率,从而更深刻地分析和验证攻击模型的有效性。另外,在每次仿真实验中,本文分别用“Expected”和“Practical”代表理想通信和CSMA/CA协议影响下的双花攻击结果。假设无线区块链的无线信道中传输单个数据包的平均有效负荷E[P]=1 024字节,每个交易的大小为64比特。那么,无线信道一次可以携带的交易数量最大为l=128。同时,设定无线区块链中总共参与Tangle共识网络的节点数量n=50,传输时延h=0.5,每个节点缓存队列的长度k=10,和Tangle共识网络的认证阈值ω=1 000。同样的,归一化处理攻击者发动双花攻击的时间,即设t0=0。
在第一个实验中,固定诚实节点和攻击者的新交易到达率,变化攻击者的双花攻击持续时间来分析成功的概率。换句话说,固定了诚实节点和攻击者的算力,那么Tangle共识网络中下一个交易到达的概率p和q也是恒定不变的。不同网络负载下,双花攻击持续时间和成功概率分别如图7,8所示。2条曲线的双花攻击成功概率随着攻击时间的增大而增大。此外,在攻击者花费相同的攻击时间,“Expected”场景的成功概率明显要大于“Practical”下的概率。由于CSMA/CA协议对交易的接入控制作用,交易在成功接入到网络中需要加入多次退避重传花费的平均时间E[D1],这也就是2条曲线出现差距的原因。更为重要的是在高负载时,攻击者要想成功赢得双花攻击必须得延长攻击时间。当节点数量n非常大时,高负载下单个诚实节点的新交易到达率增大,攻击者必须花费接近n倍算力来与诚实节点维护的分支对抗。与此同时,高负载下2条曲线的差距明显增大,这是无线信道流量增大引起的平均退避时间增大而导致的。
在第3个实验中,当前网络为低负载时设定λ=5。变化攻击者的交易到达率μ从0到60。“Expected”曲线的双花攻击成功的概率随着攻击者的交易到达率μ的增大而增大,如图9。当攻击者的交易到达率达到区块链系统的一半时,此时双花攻击一定能够成功。然而,在μ≥25.6时,“Practical”曲线的双花攻击成功的概率随着攻击者的交易到达率μ增大到2%后趋于稳定。与此类似,图10的2条曲线也有类似的趋势,当μ<25.6时,“Practical”曲线的双花攻击成功的概率一直呈上升态势。在此之后,它随着攻击者的交易到达率μ增大后一直保持在1.3%。形成对比的是,“Expected”曲线的双花攻击成功的概率将随着攻击者的交易到达率μ增大到1。根据前面的分析,仿真结果说明了攻击者一次能够广播的交易数量被CSMA/CA协议限制为无线信道的最大传输容量。因此,这意味着攻击者的能力被无线网络的传输能力所限制。

图7 变化攻击时间的概率图(低负载)Fig.7 Successful attack probability vs. duration time of the double-spending attack (low load regime)

图8 变化攻击时间的概率图(高负载)Fig.8 Successful attack probability vs. duration time of the double-spending attack (high load regime)
5 未来展望
本文通过研究基于CSMA/CA网络协议的无线局域网中攻击者进行双花攻击的成功率,证明了通信场景中通信协议的使用对安全性具有提升作用。但限于当前基于DAG共识机制的无线区块链网络平台较少,实际操作较为困难,因此,本文的不足之处主要着眼于理论分析,并未在实际区块链系统上进行部署。在接下来的工作中,考虑通过搭建实际无线区块链网络平台,在平台中部署相关通信协议,分析无线区块链下的安全与性能。

图9 变化攻击者交易到达率的概率图(低负载)Fig.9 Successful attack probability vs. new transaction arrival rate of the attacker (low load regime)

图10 变化攻击者交易到达率的概率图(高负载)Fig.10 Successful attack probability vs. new transaction arrival rate of the attacker (high load regime)
6 结束语
针对区块链的安全问题,本文以最具代表性的双花攻击为例,建立了在WBN中的双花攻击过程模型。具体而言,攻击者通过离线方式提前构建寄生链,同时在真实付款交易被区块链验证时广播该寄生链,攻击者通过延长攻击时间和增加计算能力来提高双花攻击的概率。在无线连接的场景下,攻击者和诚实节点都需要不断地消耗本地计算资源来发布新交易,这是为了不断维护自己的DAG账本分支以免被系统抛弃。那么,攻击者和诚实节点都是在以DCF机制来竞争无线信道广播新交易,势必会受到无线信道传输容量的限制。也就是说,网络中所有节点的计算资源都会被CSMA/CA协议束缚。为了定量地体现无线连接方式区块链安全的变化,本文以攻击过程时间为基本单位,给出了2种网络流量负载下的双花攻击概率表达式,同时与理想通信下的概率表达式形成对比。最后,改变攻击者的算力或攻击时间,以多次仿真实验的结果来直观双花攻击概率的变化情况。本文发现,在网络流量为高负载时,攻击者的计算资源被传输容量大大限制,提高了区块链的安全性。然而,当网络的传输能力足够大时,拥有丰富计算资源的攻击者依然以较高概率成功实现双花攻击。

