基于随机游走扩散映射的降维算法

薛艳锋 王三虎 高志娥 高永强

1(山西大学计算机与信息技术学院 山西 太原 030006)2(山西大学复杂系统研究所 山西 太原 030006)3(吕梁学院计算机科学与技术系 山西 吕梁 033000)

0 引 言

降维是通过线性或非线性的映射关系将高维数据转换到低维数据的过程，且该低维数据代表原始高维数据的主要成分，并能描述原始高维数据的空间分布结构。一般情况下，由于降维后的数据更易于被分类、识别、可视化、存储等，故降维在机器学习[1]以及数据可视化[2-3]领域受到越来越多的关注。

现有的降维算法主要分为线性降维和流形学习降维，其中：线性降维仅对于数据维数相对较低且具有全局线性结构的数据有着良好的降维效果，代表算法包括主成分分析[4-5]、线性判别分析[6-7]、多尺度分析[8]算法等；流形学习降维主要是把高维空间的内在结构或本质特征在低维空间尽量得以保留，代表算法包括局部线性嵌入[9]、核主成分分析[10]、ISOMAP[11]算法等。然而，在实际的科学研究中，需要一种统一的降维算法，使得线性降维效果与线性降维算法相当(本文选择的参照对象为主成分分析算法)，同时流形学习降维效果尽可能合理(参照对象为局部线性嵌入)。

为此，本文利用数据点属性之间的欧氏距离定义了数据随机游走的转移概率矩阵A，然后通过归一化矩阵A得到马尔可夫转移矩阵M(该矩阵M描述数据的离散扩散过程)，其次通过该矩阵M得到对应的拉普拉斯矩阵L，最后按照该矩阵L的特征值升序排列对应的特征向量，按照累积特征值比例，原始数据依次投射到对应特征向量(从第2个特征向量开始)上。通过实验结果表明，在线性降维方面，本文算法与主成分分析算法相当，而局部线性嵌入失败；在流形学习降维方面，主成分分析算法失败，而本文算法虽然不及局部线性嵌入，但反映的内在结构一致。

1 算法描述

1.1 局部线性嵌入算法

局部线性嵌入的核心思想是假设数据在较小的局部是线性的，也就是说一个数据可以由它邻域的几个样本来线性表示。具体过程如下：假设有样本x1，在该样本的原始邻域中用K近邻思想找到其中的K(超参数)个样本x2,x3,…,xk+1且可以由它们线性表示：

x1=w1,2x2+w1,3x3+…+w1,k+1xk+1

(1)

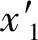
(2)

最后，通过均方差定义损失函数并求其权重系数：

(3)

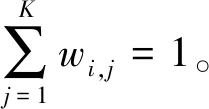
1.2 随机游走扩散映射算法

局部线性嵌入的局部线性关系只在样本附近起作用，离样本远的样本对该样本的线性关系没有影响且影响样本点是确定的。随机游走扩散映射的思想是K近邻思想的扩展，即所有其他样本都起作用，只是距离较近的样本比距离较远的样本影响更大且影响样本点是随机的。

随机游走扩散映射算法的具体步骤如下：

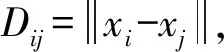
2) 使用这些距离来定义数据上的随机游走，从点i到点j的跳跃概率为：

(4)

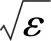
M=Σ-1A

(5)

设原始数据点降维的映射关系为f，则f(i)(i=1,2,…,N)为低维空间的坐标点,通过目标函数Φ(f)求其映射关系f：

(6)

4) 令f=[f(1)f(2) …f(n)]T且fTf=1，并求其马尔可夫转移矩阵M的拉普拉斯矩阵L=I-M，则式(6)可化为如下矩阵形式：

(7)

即转化为求特征值问题Lf=λf，其中λ表示拉普拉斯矩阵L的任一特征值。

5) 按照拉普拉斯矩阵L的定义以及对称矩阵的性质可知，存在最小的特征值λ1=0。按照特征值升序排序λ1≤…≤λN,则任一数据x映射到q维实数空间的坐标为：

(8)

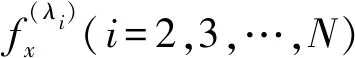
2 实 验

2.1 人造数据(线性降维)

该人造数据集为小世界网络[12-13]，通过Python库NetwordX[14]下面watts_strogatz_graph(n,k,p)函数生成，其中：n表示节点个数；k表示环状的邻居个数；p表示每条边的重连概率。本文选择节点个数n为100，k从{2,4,6,8,10,12,14,16,18,20}中等概率随机选择，p从{10-1,10-2,10-3,10-4,10-5,10-6,10-7}中等概率随机选择，重复执行该函数生成2 000个小世界网络，每个网络的特征表示为三元组(边密度，开三元组密度，闭三元组密度)[13]，最后依据该特征删除重复数据最终得到实验数据1 317条。该三元组特征降为1维后，为了更好可视化降维效果，需要经过归一化处理且在散点图中以纵坐标轴显示，左右总邻居数以横坐标轴显示。其中各个标题名称括号里的数字为超参数设置，比如图1(b)括号中数字为扩散映射的软阈值带宽，图1(c)和图1(d)括号中数字为局部线性嵌入的最近邻个数。

从图1可知，主成分分析与扩散映射降维之后的特征与小世界网络的左右总邻居数有着严格的对应关系，这是由于watts_strogatz_graph(n,k,p)函数生成的边数k是确定的，而重连概率p虽然是随机值，但由于有开三元组密度和闭三元组密度对该生成的小世界网络进行描述，故降维之后仍能保持与小世界网络左右总邻居数的严格对应关系，而局部线性嵌入降维之后无法刻画这种严格的对应关系。而且，主成分分析算法与扩散映射的累积方差贡献率分别为98.95、98.93，定量说明了随机游走扩散映射算法在线性降维方面与主成分分析算法效果相当。

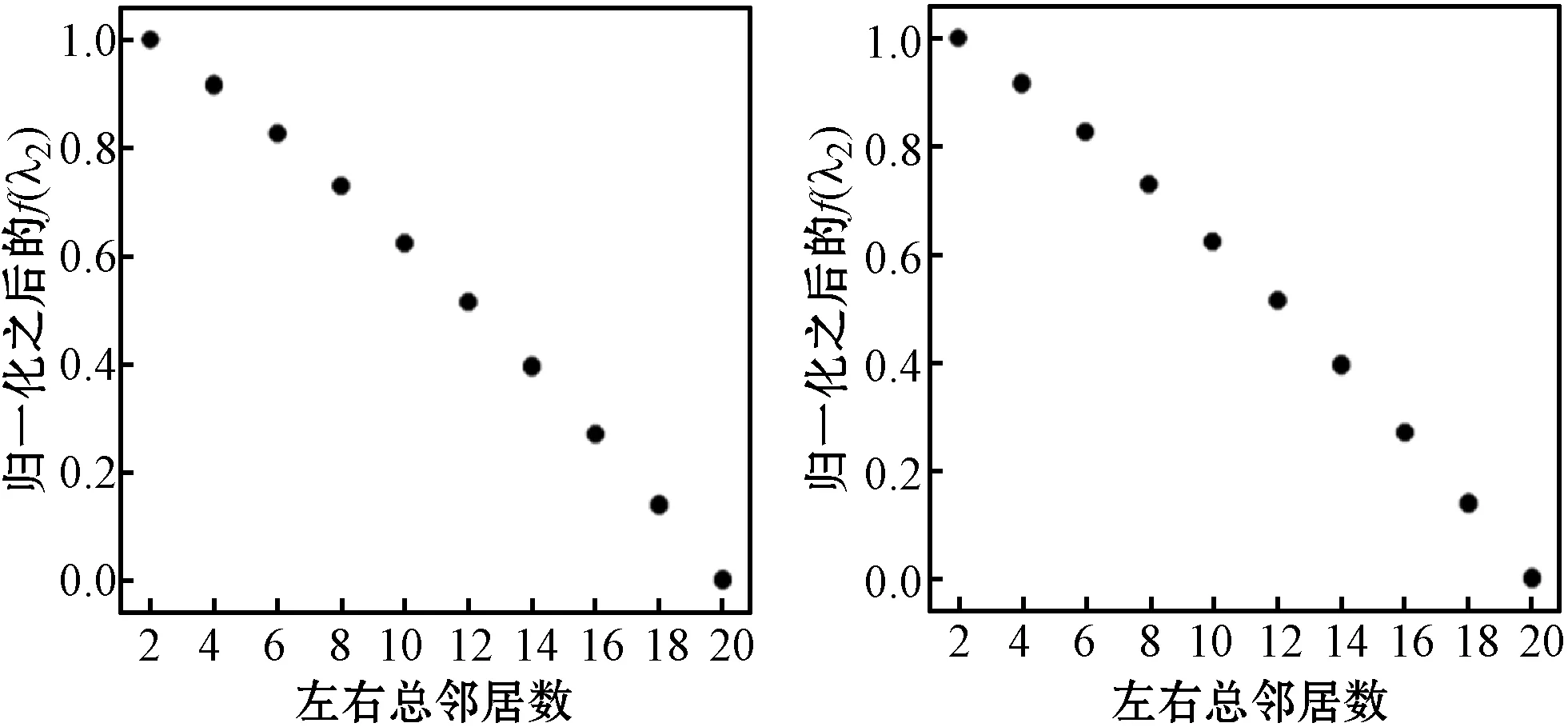
(a) 主成分分析 (b) 扩散映射(5)

2.2 真实数据(线性降维)

出于可视化的考虑，真实数据集为鸢尾花数据集，数据降为2维，且每一类数据通过散点图分别以不同的形状显示。如图2所示，主成分分析与扩散映射算法把“setosa”类与其他两类明显分开，局部线性嵌入算法也达到同等的分类效果；同时，主成分分析与扩散映射算法基本把剩余两类(versicolor与virginica类)基本分开，而局部线性嵌入把这两类嵌入到二维空间的同一坐标，即分类失败。

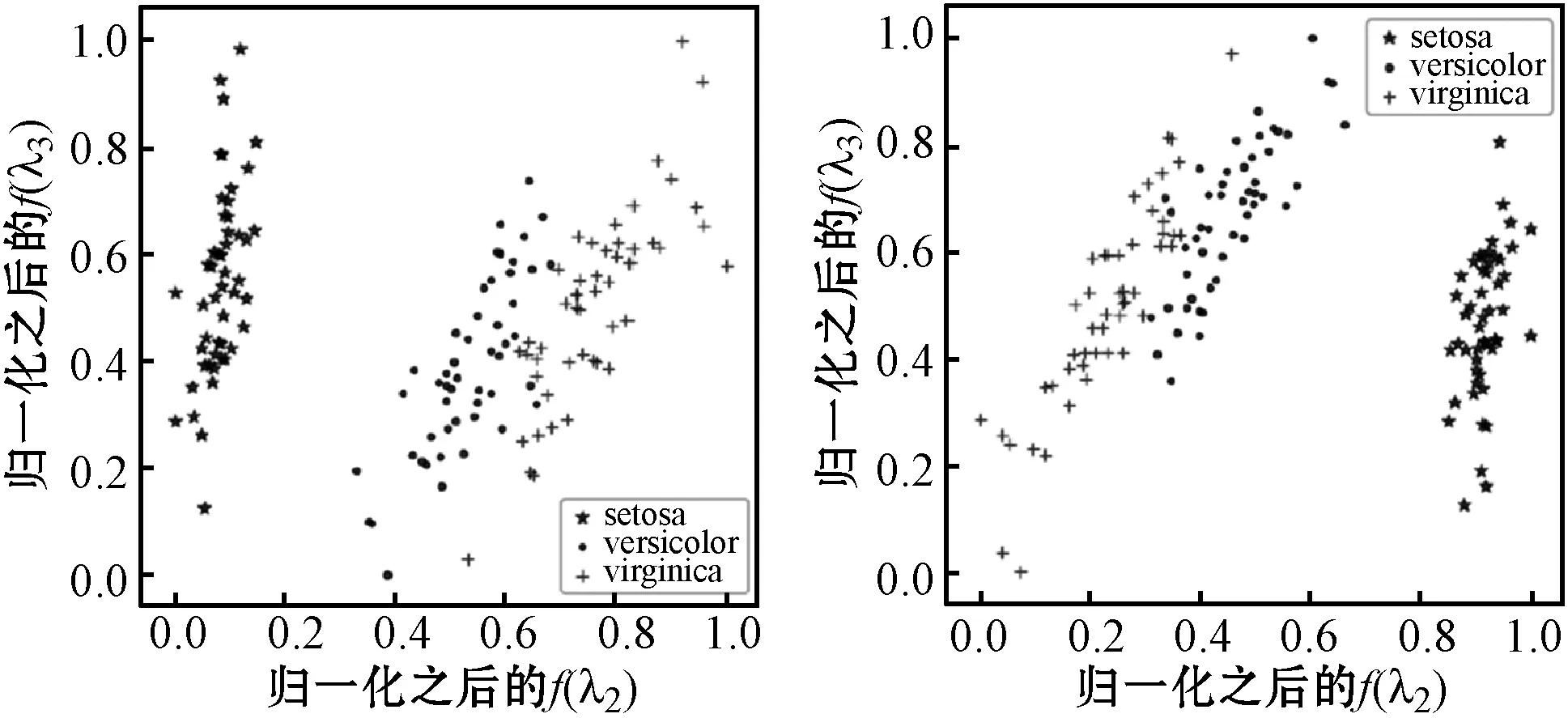
(a) 主成分分析 (b) 扩散映射(10)

2.3 人造数据(流形学习降维)

该人造数据集为S-curve数据集[15]，即流形数据集(一个不闭合的曲面)，三维显示如图3(a)所示(括号中数字为数据点数量)，流形曲面具有数据分布比较均匀且比较稠密的特征，流形学习降维就是将流形从高维到低维的映射过程，在该降维过程中，流形的高维特征尽可能在低维空间得以保留。在本文，就相当于把S-curve数据集从三维空间投影到二维空间，即把S-curve数据集展开到二维空间，展开的过程就是流形学习降维的过程，就像两个人拉开一样(如图4所示)。

(a) S-curve数据集(1 000) (b) 局部线性嵌入(110)

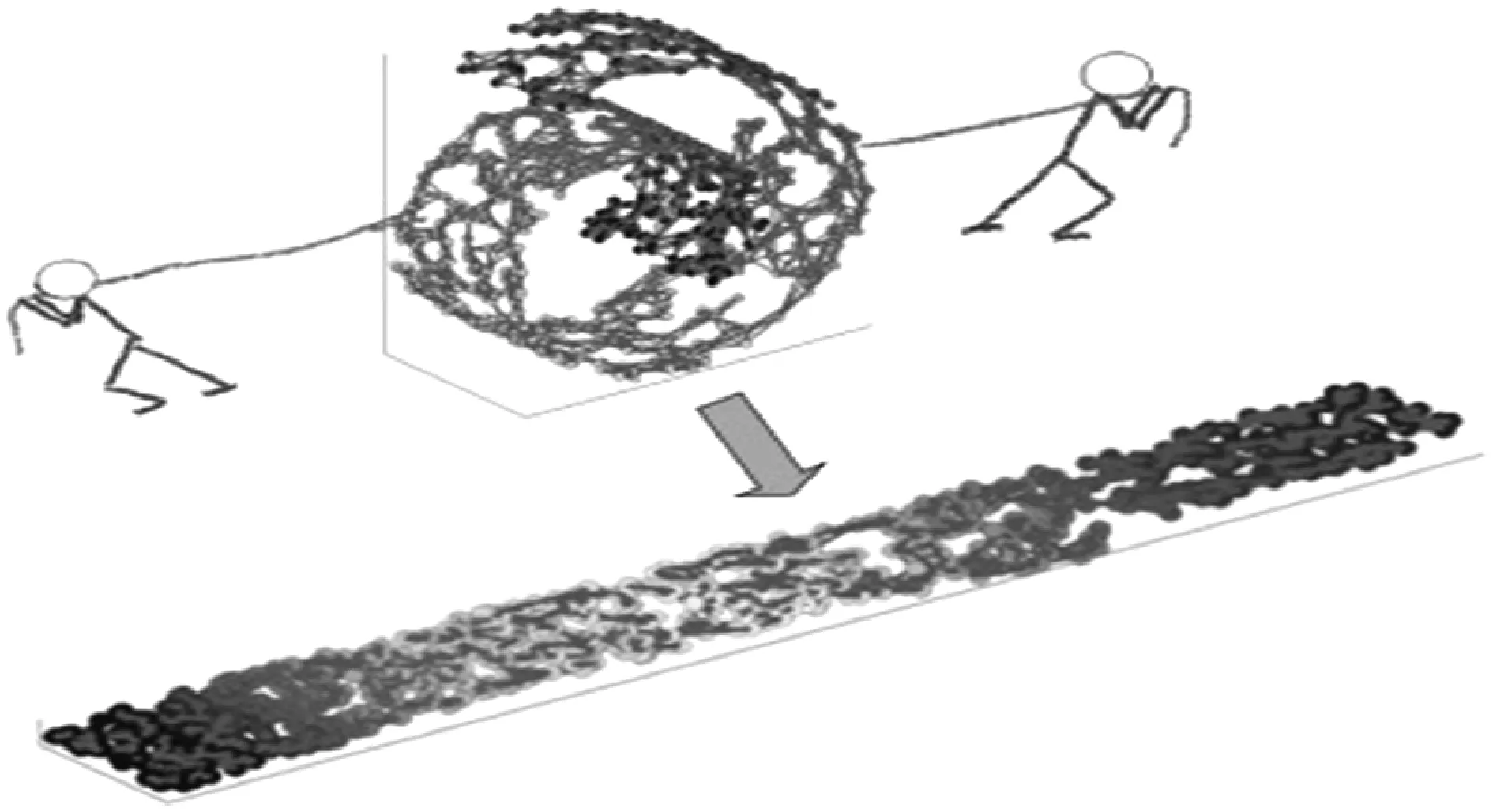
图4 流形学习降维示意图

由图3(b)可知，局部线性嵌入降维基本成功，即成功展开到二维平面。虽然左右两端没有展开，即在二维平面内有数据点重叠现象，但是设想从左右两边观察S-curve数据集的话，确实最下面与最上面互相重叠，且把三维空间下面的数据点映射到二维空间的左面，上面的数据点映射到二维空间的右面符合人的直观认识。由图3(c)可知，主成分分析算法流形学习降维失败，虽然“S”型轮廓从3维空间可以前后观察得到，但流形学习降维的目的是展开该数据集，且主成分分析算法把上面的数据集映射到二维空间左面，下面的数据集映射到二维空间右面不符合人的直观认识。图3(d)为扩散映射的降维效果，从展开效果看，不及局部线性嵌入，但对比局部线性嵌入算法，扩散映射降维算法左右两端对称的V字结构与原始S-curve数据集从三维空间左右观察有数据点重叠一致，且二维空间展开效果与人的直观认识一致。最后，三个算法就流形学习降维的效果比较如表1所示。

表1 流形学习降维效果比较

3 结 语

本文算法在线性降维效果方面，与主成分分析算法相当，局部线性嵌入完全失败；而在流形学习降维方面，对标局部线性嵌入，主成分分析算法在展开效果与直观认识上全面失败，而扩散映射在展开效果上虽然不理想，但与左右两端数据点重叠结果相一致，且符合直观认识。

今后的研究方向是改进扩散映射算法，使它在流形学习降维效果有所提升，比如设计随机游走的路径以及步长，设计更合理的距离度量以及转移概率等。