“互联网+”背景下“一阶线性微分方程”混合式教学探析
别群益 杨雯靖 周艳平
(三峡大学理学院,湖北 宜昌 443002)
0 引言
常微分方程中“一阶线性微分方程”是最基本也是最常见的一类方程。不论是数学专业的常微分方程[1,2]还是非数学专业的高等数学[3]课程,该知识点是要求学生熟练掌握的。混合式教学法是将传统面对面“线下”教学与以现代信息技术为平台的“线上”教学进行有机融合的一种新型教学模式[4]。“互联网+教育”背景下,海量的学习资源使学生对知识的获取更加迅速、便捷,名校名师的优质在线教学强烈冲击着传统的数学课堂教学。因此,基于优质在线教学资源的课堂教学改革势在必行。以高等数学课程中“一阶线性微分方程”教学内容为例,我们探索线上线下混合式教学的一些具体做法。
求解一阶线性微分方程,常用的方法是常数变易法。该方法是由法国著名数学家Lagrange发现的。所谓常数变易法,是先求解一阶线性非齐次微分方程所对应的齐次方程,将所得通解中的常数变为一个未知函数。为了求出这个未知函数,将该含有未知函数的解代入原方程解出这个未知函数,从而得到原方程的通解。尽管常数变易法在教材上给出了详细的讲解并给出了一些具体例子,但学生在运用该方法时,总感觉是知其然而不知其所以然。对于该内容的教学,我们考虑分三个阶段进行。即课前预习、课堂探究和课后练习。其中课前预习和课后练习放在线上进行,而课堂探究是教学的主战场,在预习的基础上进行线下探究式学习。
1 课前预习
课前预习的开展主要是在线上进行。首先让学生在互联网上观看一些关于常数变易法的视频,完成老师事先准备好并放在班级QQ群上的电子资料。这些资料主要是帮助学生弄清楚为什么可以将齐次方程通解中的常数变换成一个函数。课前预习所达到的目标是学生能够回答如下问题:
问题1:什么是一阶线性微分方程以及对应的齐次微分方程?
问题2:常数变易法的解题步骤是什么?
问题3:由常数变易法得出的求解一阶线性微分方程的求解公式是什么?
问题4:为什么可以进行常数变易?
其中前三个问题均可以在教材上通过学生的预习找到答案,但问题4是难点。为帮助学生课前思考并进行线上讨论,老师可设计如下资料:
一阶线性微分方程的一般形式为:

其中p(x)和q(x)都是x的连续函数。
为了求解一阶线性微分方程(1),通常教材主要介绍的是常数变易法。并且由常数变易法可以得出方程(1)的一个求解公式。
首先,求解方程(1)对应的齐次线性方程

通过变量分离,可得该方程的通解为

这里C是任意常数。因为一阶微分方程的通解中只能含有一个任意常数,故其中的不定积分-∫p(x)dx只需求出一个原函数即可。
其次,为了求出一阶非齐次方程(1)的通解,可以将方程(1)右端项q(x)移到左边变成
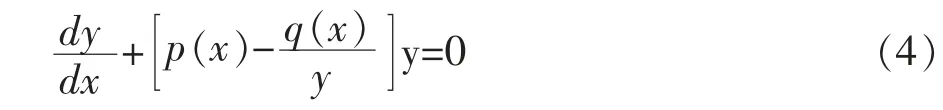
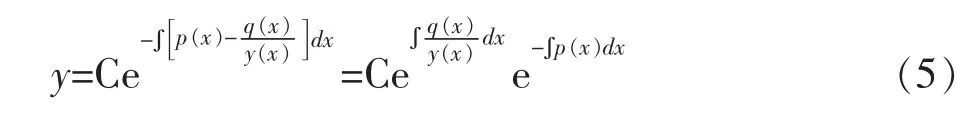

其中u(x)是一个待定函数。为了求出u(x),首先将式(6)关于x求导,得
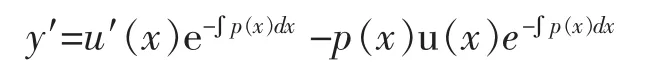
将y与y′代入方程(1)得
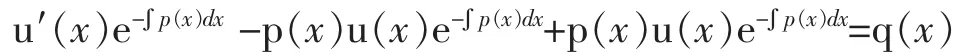
即

两边积分得
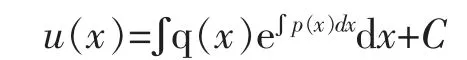
将上式代入(6),有
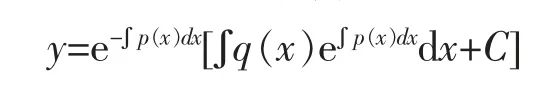
上式就是一阶非线性微分方程(1)的通解。需要说明的是式中不定积分所表示的是对应被积函数的某一个特殊的原函数。
通过比较(3)和(6)两个式子可知,为了求解一阶线性非齐次方程(1)的通解,我们先求出对应齐次方程的通解,然后将其中的常数C变为一个待定函数u(x),将该解代入原方程求出待定函数u(x),从而得到一阶线性非齐次方程(1)的通解,这就是通常所说的常数变易法。
2 课堂探究
课堂是教学的主要阵地,对于“一阶线性常微分方程”知识点的探究,课堂上主要呈现两个方面的内容:常数变易法的本质;积分因子法的探究。对于常数变易法的本质,由于学生课前通过线上的视频以及电子资料预习了,所以这部分内容特别是式(5)的推导,教师可以在课堂上对于常数变易法作小结,让学生再次领会常数变易法的本质。
积分因子法是在学习完常数变易法之后,通过分析常数变易法的求解过程,举一反三地引入的方法。该方法在高等数学教材上一般是没有呈现出来的。而这种方法的优点是容易理解,且相比常数变易法,计算更简洁。
接下来探究积分因子法。从常数变易法的求解过程中,特别是从(6)和(7)这两个式子中可以探索出一些新的结果。具体地,由(6)式可知
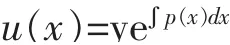
将其代入(7)式并展开得

即
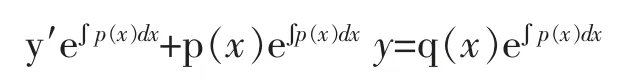
也就是
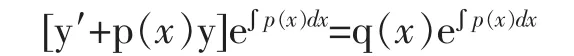
上式实质上是在原方程两边同时乘以因子e∫p(x)dx[注意到这里p(x)是已知的连续函数],这样可使方程转化为(8)的形式,从而再利用不定积分求出原方程的通解。这种求解方法可称之为积分因子法。
对于积分因子法,也可以从另外一个角度进行探究。首先让学生思考如下问题:
问题5:当p(x)=0时,方程(1)如何求解?
问题6:当p(x)≠0时,方程(1)左边的两项能否进行合并,使之成为一个关于x的函数a(x)和未知函数y的乘积的导数,即左边写成的形式?
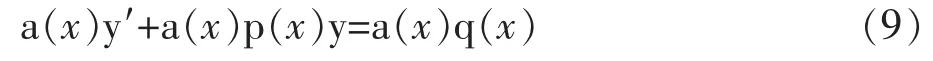
为了确定函数a(x),使得(9)式左边能够拼凑成导数形式将其展开得:
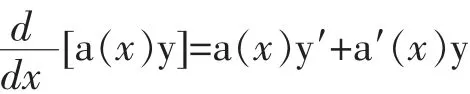
为了和(9)式左边一致,函数a(x)需满足
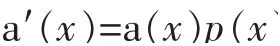
这里p(x)是一个已知函数。
显然未知函数a(x)满足的是一阶线性齐次微分方程:
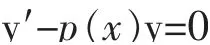
为解此方程,将其分离变量得
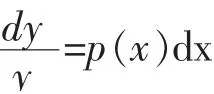
两边积分,有

这里只需找到一个特解y就可以作为需要的函数a(x),所以根据(10),找到一个y,使其满足:
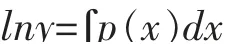
即y=e∫p(x)dx,所以要找的函数a(x)是e∫p(x)dx。这样式(9)变为:
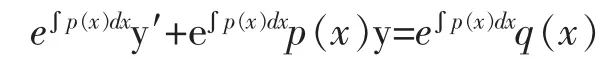
也就是
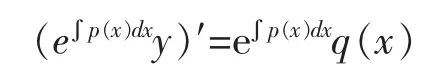
两边积分得
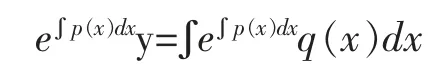
所以
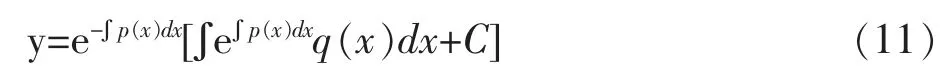
这里C为任意常数,其中的不定积分只表示对应的被积函数的一个原函数。式(11)可以作为求解一阶线性微分方程通解的公式。若直接套用该公式求解,往往称之为公式法。
教学过程中教师可以让学生思考如下问题:
解:为了将左边写成一个导数的形式,由于p(x)=-根据前面的分析,两边同时乘以函数需要指出的是虽然这个不定积分有无穷多个原函数这里只需取一个函数即可。这样原方程变为
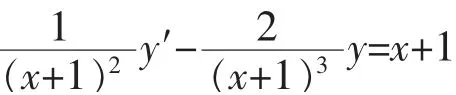
上式左边可以写成导数的形式,即
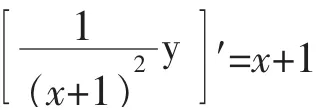
两边积分得
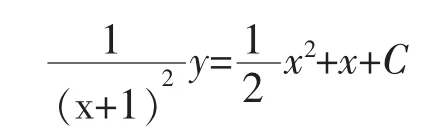
所以,原方程的通解为
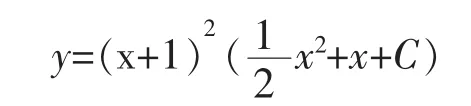
问题8:求方程y′-ytanx=secx满足y(0)=1的特解。
解:这里p(x)=-tanx,计算其中为C任意正常数。在x=0附近选取一个积分因子cosx,原方程两端同乘以这个积分因子,得:
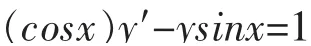
即[(cosx)y]′=1,也就是(cosx)y=x+C。由初始条件y(0)=1,可得C=1,故所求微分方程的特解为:
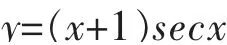
3 课后练习
课后练习作为电子资料放在QQ班级群里。学生先独立思考,然后师生在群里进行讨论答疑。课后练习题如下:
求解下列微分方程(要求用三种方法求解,即公式法、常数变易法及积分因子法)。