基于关键用例获取的测试用例排序方法

范书平，万 里，姚念民，张 岩，马宝英

（1.牡丹江师范学院计算机与信息技术学院，黑龙江牡丹江 157012；2.天津大学智能与计算学部，天津 300350；3.大连理工大学计算机科学与技术学院，辽宁大连 116024；4.宿迁学院信息工程学院，江苏宿迁 223800；5.牡丹江医学院卫生管理学院，黑龙江牡丹江 157011）

1 引言

回归测试是指修改了旧代码后重新进行测试，以确认修改没有引入新的错误或导致其他代码产生错误［1］.据估计，回归测试在整个软件测试预算中约占80%［2］.为了降低回归测试的成本，近些年国内外学者对高效自动化的回归测试技术展开了深入的研究，测试用例排序技术（Test Case Prioritization，TCP）［3］是目前研究的热点之一.测试用例排序技术在不减少测试用例数量的情况下，按照某种准则对测试用例进行排序，使得有较高优先级的测试用例优先执行［4］，该技术可以有效减少回归测试工作量［5］，其目标是更早揭示程序中的缺陷，从而降低回归测试的成本.

目前，许多学者研究了多种性能指标和技术来实现回归测试用例的优先排序，以最大化回归测试的有效性.Fang 等人［6］研究修改的条件/分支覆盖测试用例排序方法；Chen 等人［7］考虑用半监督学习改进聚类过程，并应用程序切片技术进行用例的排序；Noor 等人［8］则提出了基于历史故障数据的排序方法，该方法考虑了测试用例之间的相似性；潘伟丰等人［9］提出了一种基于复杂软件网络的回归测试用例优先级排序方法，该方法评价类的测试重要性，同时结合测试用例的覆盖信息，对测试用例进行排序；张卫祥等人［10］应用遗传算法，石宇楠等人［11］应用协同进化算法，Nayak 等人［12］应用粒子群算法分别实现了测试用例的排序.多数TCP技术使用结构覆盖作为衡量测试用例优先级的指标［12，13］，Mukherjee 等人［1］对2001—2018 年的90 篇关于测试用例排序的学术论文进行了研究，结果表明基于覆盖信息的排序技术应用得最为广泛，这类技术的目标［14］是尽可能早地实现代码覆盖.

贪心算法是解决测试用例排序问题的常用算法［11］，包括total 策略与additional 策略.Rothermel 等人［15］最早提出了面向覆盖的TCP技术，并应用这两种策略设计了不同的排序方法，结果表明所提方法能有效提高测试用例的缺陷检测率.作为该工作的延伸，Elbaum等人［16］则将测试用例排序划分为功能级技术、语句级技术的排序方法，在方法中引入节约系数，将平均缺陷检测百分比（Average Percentage of Fault Detected，APFD）转换为效益模型.Hao 等人［17］应用了集成线性规划，提出了基于最优覆盖的优先级排序技术，研究表明，与基于贪心算法的TCP 技术相比，所提出的排序技术在缺陷检测率或执行时间上没有明显弱势.张娜等人［18］则提出基于多目标优化的TCP 方法，有效缩短了软件测试时间.Jiang等人［19］提出了基于覆盖率的ART技术，其目的是尽可能地扩展代码覆盖空间.陈梦云等人［20］则在基于覆盖的total 策略与additional 策略中引入了圈复杂度，实现了测试用例优先级，提高了错误检测的有效性.

在基于分支覆盖的测试用例排序技术中，典型的total 策略总是将覆盖分支最多的候选用例加入到已排序序列中，而additional 策略则选择覆盖新分支最多的用例［15，21］.也有TCP 技术根据用例的输出覆盖程序切片情况，给在相关切片中覆盖更多语句与分支的用例分配更高的权重［22］.Mahdieh 等人［23］则在代码覆盖（包含语句和分支单元）的基础上，应用神经网络进行缺陷预测，以评估代码单元的故障倾向性.Huang 等人［24］结合代码覆盖与组合覆盖提出了一种新的覆盖准则，将该覆盖准则应用于测试用例排序中，并通过与两种贪心策略进行对比，验证了所提方法的有效性.此外，Fang 等人［21］在测试用例运行程序后，根据各用例覆盖程序实体的有序序列计算用例间的相似性，提出了面向语句和分支覆盖准则的测试用例排序技术，提高了排序用例的缺陷检测能力.

上述测试用例排序方法往往只考虑单一用例对测试目标的重要程度，并未有效利用已排序用例覆盖程序真假分支的均衡情况.这种不均衡性导致用例覆盖程序分支的偏离影响会更大，尤其对于大型复杂程序，分支或者循环结构较多，这种偏离程度尤为突出.然而，在测试用例排序中考虑用例对程序代码测试均衡的研究还很少并且不够深入.

本文的主要贡献如下：

（1）在测试用例排序技术中引入用例覆盖程序各分支的偏离程度；

（2）应用测试用例覆盖程序新分支情况与用例覆盖程序分支的偏离程度来计算候选用例的权重，并据此选择关键用例进行排序；

（3）提出了基于关键用例获取的排序算法来有效解决测试用例排序问题；

（4）将所提出的方法应用于典型程序，验证了方法的有效性.

2 基本概念

为了便于阐述，下面给出几个基本概念.

2.1 测试用例排序

测试用例排序问题可以定义［20］为给定测试套件T，T中所有测试用例排序的集合O，以及从O到实数集映射函数f；测试用例排序的目标为找到一个序列子集o∈O，满足∀o′∈O,f(o)≥f(o′).其中，f函数的作用是度量测试用例排序的有效性，为了提高给定测试套件的缺陷检测率，f函数通常为平均缺陷检测百分比（APFD）函数，其取值范围为［0，1］，APFD 值越大，缺陷检测率越高.

2.2 sigmoid函数

sigmoid 是一种激活函数，该函数常用作二分类的概率以及输出神经元，应用它可以把一个实数映射到区间（0，1），该函数的定义为

2.3 基于覆盖的测试用例排序技术

基于覆盖的测试用例排序方法通常将源代码划分为层次结构单元，例如包、文件、方法和语句，并定义这些单元的覆盖率，单元覆盖率［23］可以描述如下.

假设已经将被测程序的源代码划分为多个单元，U={u1,u2,…,um}.对于每个测试用例tk与代码单元uj，Cover(k,j)表示测试用例tk是否覆盖单元uj，如果被测代码的单元是语句，则覆盖范围为0 或1.用n(n＞0)表示代码单元的数量，通常将测试用例tk的总覆盖范围Cover(k)定义为

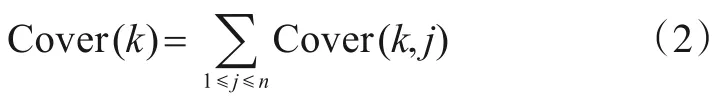
2.4 用例偏离度

已排序用例与候选用例tk运行被测程序后，覆盖程序中第w个分支节点真假分支的用例数目的差异，称为用例tk对第w个分支节点的用例偏离度（简称为用例偏离度），表示为BPkw，见3.1.3节中的式（7）.

2.5 关键用例

测试用例运行程序后，每次从候选用例中选择用例进行排序时，根据候选用例覆盖程序新分支数量以及用例偏离度，按照3.1.4 节中的式（8）计算各候选用例权重，得到权重最大的候选用例定义为关键用例.

3 基于关键用例获取的测试用例排序方法

3.1 关键用例的获取

为了便于分析，本文将循环节点按照循环体执行或者不执行转化为含有两个分支的情况，而switch语句本身也可以转换为双分支结构，为此，以下讨论中将分支节点与循环节点统称为分支节点，且仅考虑一个分支节点有两个分支的情况.

3.1.1 建立用例覆盖分支矩阵

首先，根据测试用例覆盖程序各分支节点真假分支情况，建立测试用例覆盖分支矩阵.假设当前测试套件中含m(m＞0)个测试用例，被测程序含n个分支节点，对应有2n个分支节点的真假分支，通过统计第w(1 ≤w≤n)个分支节点的真分支bwT与假分支bwF的被测试用例ti(1 ≤i≤m)的覆盖情况，得到用例覆盖分支矩阵，记为covm(2n)，矩阵中的行代表测试用例ti覆盖各分支节点的真假分支的情况，矩阵中的奇数列表示各测试用例覆盖各分支节点的真分支的情况，矩阵中的偶数列则代表不同的测试用例覆盖各分支节点的假分支的情况，covm(2n)表示为

其中，当j为奇数时，

3.1.2 记录已排序用例覆盖程序分支情况

假设当前已排序用例总数为m′(0 ＜m′≤m)，根据3.1.1 小节中建立的用例覆盖分支矩阵covm(2n)，计算覆盖第w个分支节点真分支、假分支的已排序用例数目，分别记为sumwT与sumwF.则可以将sumwT表示为

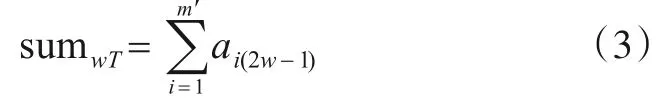
式（3）表明，覆盖第w个分支节点真分支的已排序用例数目，可以通过对矩阵cov 的第(1～m′)行中的第(2w-1)列元素求和得到.同理，可以将sumwF表示为

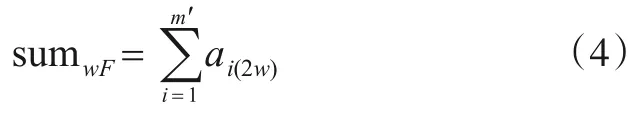
式（4）表明，覆盖第w个分支节点假分支的用例数目通过对矩阵cov的第(1～m′)行中第2w列元素求和得到.

3.1.3 计算候选用例的用例偏离度

为了考查候选用例tk是否能有效改善用例覆盖程序分支的均衡性，本文通过计算该候选用例排序后的用例偏离度来实现.候选用例tk排序后，将覆盖第w个分支节点真分支与假分支的用例数目分别记为与，则可以表示为

同理，覆盖第w个分支节点假分支的用例数目可以表示为

则tk排序后覆盖第w个分支节点真假分支用例数目的差异可以表示为为了便于计算，本文通过应用Sigmoid 函数（见式（1）），将该值规范化为（0，1）区间内的值，并将规范化后的差异性记为候选用例tk对第w个分支节点的用例偏离度BPkw，该值表示为

由式（7）可知，BPkw∈(0,1)所定义的用例偏离度实际上反应了用例tk排序后覆盖第w个分支节点的用例覆盖其真假分支的差异情况.若BPkw较大，则说明覆盖第w个分支节点真假分支的用例差异较大，说明覆盖该分支节点真假分支的用例偏离程度较大；反之，若BPkw的取值较小，说明覆盖该分支节点真假分支的用例差异小.不难得出，用例偏离度BPkw越小越好.

3.1.4 计算候选用例的权重

在候选用例tk权重的计算中，综合考虑用例偏离度及覆盖新分支的情况.根据式（7），进一步计算tk排序后所有分支节点的用例偏离情况，并将式（2）单元覆盖率中的代码单元uj表示为分支节点的真假分支，用Cover(k)表示tk覆盖新分支的数目，则可以将候选用例tk的权重表示为

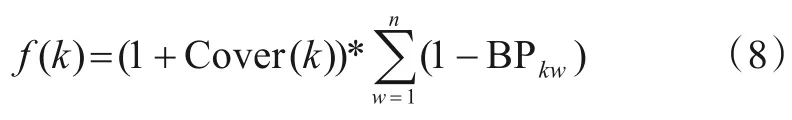
其中，Cover(k)∈[0,n].

从式（8）可以看出，候选用例权重的计算综合考虑了候选用例偏离度及覆盖新分支的能力，候选用例tk覆盖的新分支越多，tk排序后用例偏离度越小，则该用例的权重越大.此外，若某一候选用例tk虽然不能覆盖新分支，但是排序后能有效改善用例偏离度，这样的候选用例权重也较高，并会优先加入到排序序列中.

3.2 基于关键用例获取的测试用例排序算法

本文算法步骤如算法1 所示.该算法的基本思想是：首先插桩被测程序，并对算法的控制参数赋值，测试用例运行被测程序，从中选择覆盖程序语句最多的用例作为第一个已排序用例；然后根据用例覆盖程序各分支情况，建立用例覆盖分支矩阵，并据此得到用例偏离度及候选用例覆盖分支情况，进而获取关键用例进行排序，直到所有用例均已排序.

4 实验

实验中所有程序均用C 语言编写，仿真环境为VC++6.0.选择的实验程序包括space 程序、tot_info 程序、replace 程序、flex 程序与sed 程序［1］.并从space 程序、flex 程序与sed 程序中各选择两个函数进行实验.表1中列出了实验中各程序参数的设置情况，包括选择的程序代码行数（LOC）、插入缺陷数目（Faults）以及用例规模（Test Cases）.对比方法包括：根据程序实体相对执行次数，通过计算用例间距离的基于语句覆盖或分支覆盖的排序技术［21］，将这两种方法分别记为SED 与BED，选择的第三种对比方法为典型的Additional算法，记为AGA，该方法按照候选用例覆盖新语句情况选择用例进行排序［25］.

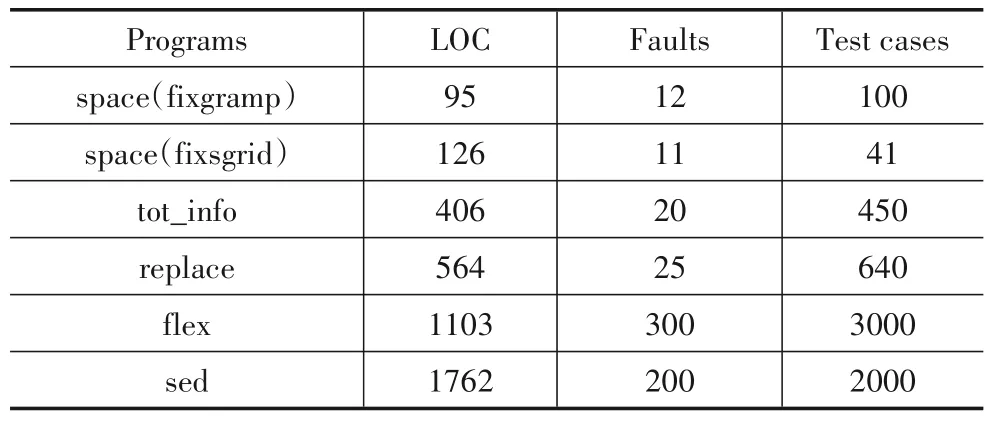
表1 程序说明

4.1 需要验证的问题与评价指标

问题1所提的测试用例排序方法的时间效率如何？

本文应用多次实验中算法的平均运行时间AT 来衡量算法的时间有效性［26］，如式（9）所示，其中Ti(1 ≤i≤total)表示第i次实验算法的运行时间，total表示总实验次数，可知AT值越小，算法的时间有效性越好.

问题2所提方法的缺陷检测有效性如何？

通过考查不同排序方法检测出各缺陷时需要执行的测试用例情况，来比较不同方法的缺陷检测性能，以验证所提方法的有效性.

问题3所提方法的缺陷检测效率如何？

用平均缺陷检测百分比APFD 来验证所提方法的缺陷检测效率，如式（10）所示，其中m′与num 分别表示测试套件包含的测试用例数和测试用例可检测出的缺陷数，TFi(1 ≤i≤m′)表示第i个缺陷第一次被检测出的测试用例在排序后的测试用例集中的次序编号.

问题4所提方法的测试用例排序序列对程序分支覆盖均衡性如何？

本文比较了不同方法得到用例排序序列的TB 值，该值表示了每个排序用例对各程序分支覆盖的平均均衡程度，计算方法见式（11）.假设排序后得到的序列为t1,t2,…,tm′，公式中BPkw表示在用例排序过程中找到的各关键用例tk对第w个分支节点的用例偏离度.

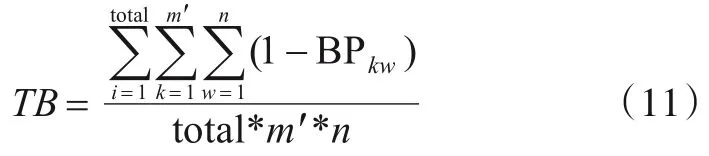
4.2 实验结果及分析

实验结果如表2、图1、图2所示.

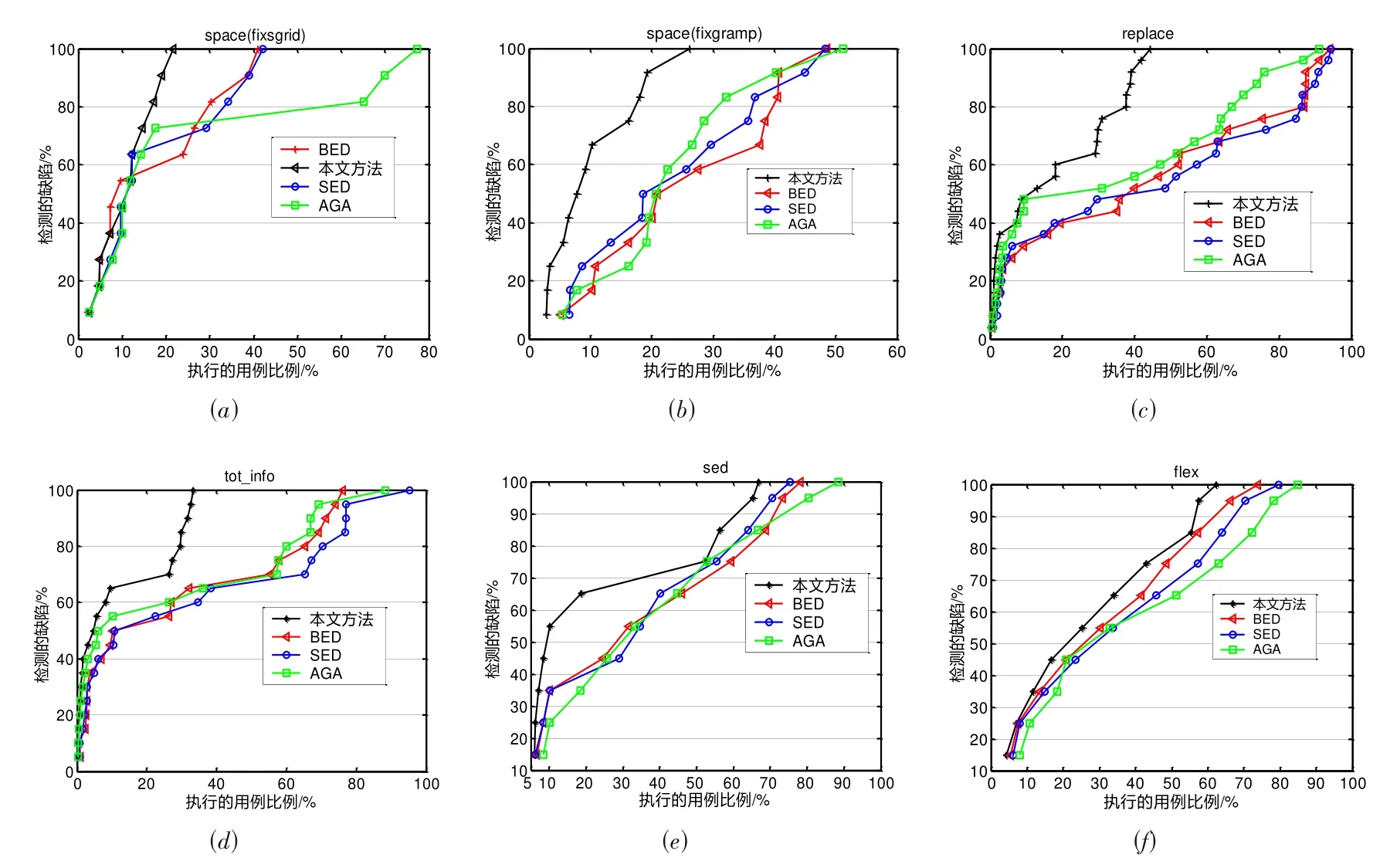
图1 测试用例检测缺陷情况

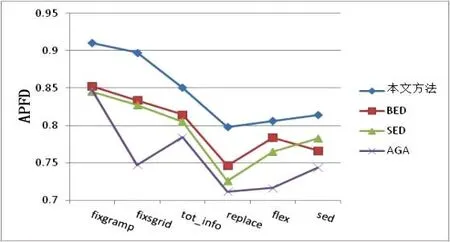
图2 不同方法的APFD值

4.2.1 运行时间的比较

从表2中运行时间上看，AGA方法的运行时间明显少于其他方法，原因是AGA 方法按照各排序用例的语句覆盖情况排序用例，计算量小，但也因此导致覆盖相同数目缺陷执行的用例比其他方法多；而本文方法的运行时间除略高于AGA 方法外，明显少于BED 方法与SED 方法的运行时间，这是因为应用BED 方法与SED方法，在用例排序时需要根据程序实体执行次数反复计算用例之间的编辑距离，计算量大.从表2 中也可以看出，除了replace 程序外，针对其他被测程序，SED 方法的运行时间比BED 方法更长；而本文方法在用例排序中仅需要计算候选用例排序后的用例偏离度与覆盖新分支数目，计算量明显少于BED 方法与SED 方法，这也验证了问题1.与BED 方法与SED 方法相比，应用本文方法的运行时间较少，能有效降低软件测试代价.

4.2.2 缺陷检测有效性的比较

为了比较不同方法的缺陷检测性能，针对不同被测程序，比较了四种方法检测全部缺陷需要执行的用例百分比情况，如表2所示.从表2中可以看出，与其他三种方法相比，应用本文提出的方法检测全部缺陷时需要执行的用例更少，也就是说，在相同的实验条件下，应用本文方法需要更少的用例即能检测出程序中的所有缺陷.

表2 运行时间与用例数目的对比

为了进一步说明本文提出的方法的有效性，实验中比较了各排序方法随着缺陷数目的增加测试用例的执行情况，实验结果如图1所示.从图1中不难看出，对于不同被测程序的六种情况，与BED 方法、SED 方法和AGA 方法相比，应用本文方法排序的用例能更早检测出程序中的缺陷；从总体上看，随着测试用例的增加，各种方法检测的缺陷也越来越多，除了图1（a）中个别缺陷检测上本文方法使用了比其他方法更多的用例外，其他情况下本文方法检测到的各缺陷执行的用例数目比其他三种方法少.从图1（a）中被测程序的执行结果来看，对于个别缺陷，应用本文方法需要执行的用例略多于BED 方法，这是因为被测程序space（fixgrid）含有的分支结构较多，BED 方法在用例排序中考虑了候选用例的分支覆盖情况，因此如果测试用例覆盖了缺陷所在分支就容易检测出这类缺陷，因此，在这种情况下，BED 方法比本文方法、SED 方法和AGA 方法更早检测出了这些缺陷，针对其他缺陷，本文方法明显优于BED 方法、SED 方法与AGA 方法.从总体上看，与其他方法相比，对于不同的被测程序，在执行相同的用例情况下，应用本文方法检测的缺陷数目更多，这也验证了问题2，与BED 方法、SED 方法与AGA 方法相比，本文的测试用例排序方法更有效.

图2 中对比了不同方法的APFD.针对不同的测试用例规模、不同的被测程序，本文方法的APFD 值要高于其他三种方法.这是因为本文方法在选择关键用例进行排序时考虑了候选用例的用例偏离度与覆盖新分支情况，使得所选择的用例要么能覆盖已选择用例未覆盖的新分支，要么能够降低用例偏离度，即能有效减少覆盖各分支节点真假分支的用例差异，使得排序的用例更均衡的覆盖程序分支，尤其是对于难以检测到的缺陷，本文方法通过更快速地达到分支覆盖的均衡，来提高程序中缺陷的检测效率.总体上看，BED方法优于SED 方法与AGA 方法，这也验证了问题3，本文方法不仅能有效地进行缺陷检测，更能提高测试用例缺陷检测的效率.

4.2.3 覆盖程序分支均衡情况的比较

针对不同被测程序比较了TB 值，实验结果如表3所示.从覆盖程序分支均衡情况上看，针对不同实验设置，应用本文方法得到的实验结果比其他3 种方法的TB 值均要高，这也验证了问题4，本文方法得到的排序序列能更均衡地覆盖程序分支.这是因为本文方法在测试用例排序过程中考虑了候选用例覆盖程序分支的均衡情况.同时，对于不同被测程序，AGA方法的TB值要高于BED 方法与SED 方法，这是因为，应用AGA 方法在排序过程中每次达到代码覆盖要求后，将重置代码为未覆盖并重新执行该算法，导致排序的用例更均衡覆盖程序分支.

表3 覆盖程序分支均衡性的对比

5 结论

测试用例排序是回归测试研究的重要内容.本文提出了一种基于关键用例获取的测试用例排序方法，在测试用例运行被测程序后，根据覆盖程序各分支用例的偏离情况，计算候选测试用例的分支偏离度，并考虑候选用例覆盖新分支情况，据此对用例进行排序.本文方法提高了软件缺陷的检测能力与用例排序的效率，但本文方法仅应用于规模有限的被测程序，下一步研究的工作重点是在规模更大的工业程序中应用本文方法，以进一步验证该方法的有效性.