结合决策系数和ESMD-TEO的集电线路故障定位方法

王晓东，王永浩，刘颖明，高 兴

（沈阳工业大学电气工程学院，沈阳 110870）

目前世界各国非常重视新能源的发展，海上风能作为一种储能丰富的可再生能源得到越来越多的利用[1-3]。在实际中集电线系统工作环境复杂、运行中易受自然灾害影响导致故障频繁发生。此外，集电线路具有的多分支和长度短的特点增加了故障定位的难度。因此，快速准确找出故障点不仅能够缩短排除故障的时间，更能降低水下维护成本。

行波法定位不受过渡电阻、系统运行条件等因素的影响被广泛应用[4-11]，准确标定行波波头是行波法故障定位的关键。文献[4-6]利用小波变换WT（wavelet transform）分解暂态故障行波信号，但检测结果受小波基和分解尺度选取的影响，选取不当将会出现较大偏差。文献[7]利用经验模态分解具有的自适应性解决了WT选取小波基和分解尺度的难题，但会出现模态混叠造成较大误差。文献[8]通过将集合经验模态分解和总体局部均值分解相结合抑制模态混叠现象，但是并不能完全消除影响。

在实际系统中，集电线分支众多是故障定位另一关键问题。现有方法一般需要采集各分支末端故障数据，且故障区段定位准确率较低。文献[12]提出一种适用于T型线路故障定位判据，但不能将其应用于集电多分支线路。文献[13-15]利用故障行波线模分量与零模分量传播时间差进行定位，有效地避免了多分支线路的影响，但零模分量衰减迅速难以检测。文献[16-18]采用多测点方法实现多分支的故障定位，但需要装设大量测点，经济性较差。

综上所述，目前集电多分支线路故障定位方案受系统分支结构的影响，难以准确定位故障区段，且需要大量的故障数据检测点，经济性和实用性较差。现有方法处理微弱行波信号过程中，故障特征并不明显难以准确标定行波波头，且定位结果受故障类型、过渡电阻等因素的影响，导致较大的定位误差。

针对上述问题，本文提出一种基于决策系数与ESMD-TEO的风电场集电多分支线路故障定位方法。仅在主集电线路两端装设故障数据采集装置的情况下，通过分析风电场内不同位置故障的决策系数，得出决策系数与故障点位置之间的映射关系，提出相对应故障支路判据。利用极点对称分解ESMD（extreme-point symmetric mode decomposition）滤除信号中的低频分量和噪声，并通过Teager能量算子TEO（Teager energy operator）对一阶固有模态函数信号IMF（intrinsic mode function）进行差分计算增强暂态故障特征，准确标定故障行波波头。利用双端故障定位算法实现主集电线路故障点定位。

1 基于决策系数的故障区段定位原理

1.1 决策系数函数的构建

如图1（a）所示，海上风电场含有多条集电线路且存在大量电源分支，导致故障区段定位准确率低，且在所有风机支路末端都配置故障数据检测装置经济性和实用性差。为此，本文提出利用各条风机支路决策系数准确辨别故障区段的方法。

为准确阐述决策系数函数的构建，在图1（b）所示含有n个终端、m个节点的主集电线路模型上进行说明。其中，M1Mn为主集电线路；MiKj(i=2,3,…,n-1;j=1,2,…,m )为风机支路。将M1和Mn设置为检测点，并作为参考点。对于系统中任意条风机支路MiKj，定义其决策系数函数LMiKj为

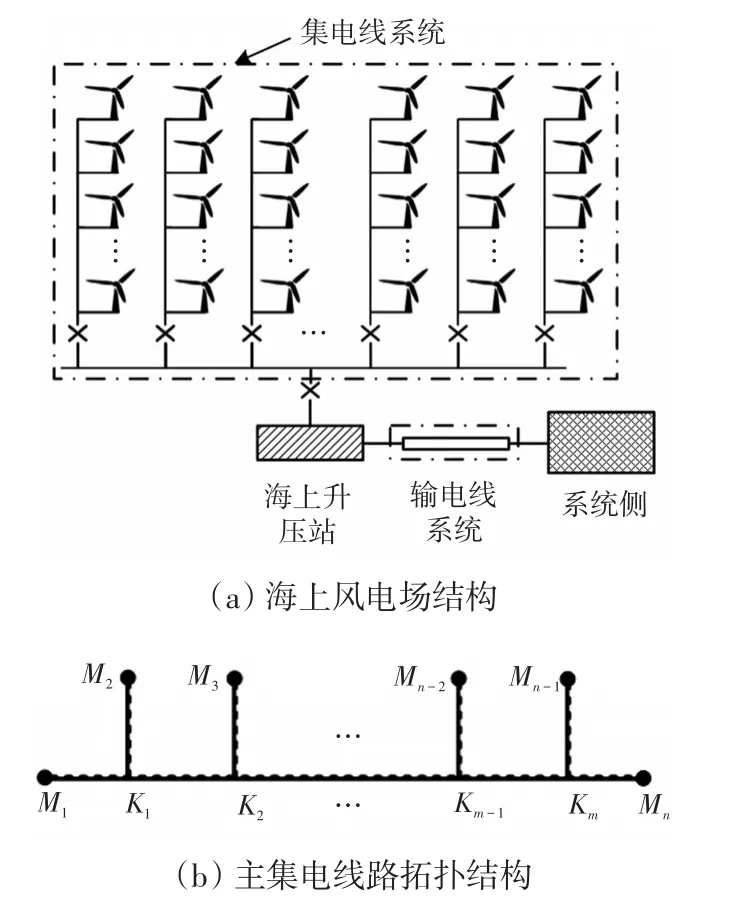
图1 海上风电场拓扑模型Fig.1 Topological model of offshore wind farm

1.2 决策系数分析

准确得到故障点到线路终端M1和Mn的距离是实现故障区段定位的关键。而集电线具有分支众多、线路短的特点导致传统单端法和双端法难以准确计算故障距离dM1F和dMnF，使所得决策系数出现较大误差造成故障支路误判的情况。为此，本文提出了一种改进的单端行波法计算决策系数。

假设故障发生在风机支路MiKj。此时，故障点到线路始端M1的故障距离可以表示为

假设故障点发生在主集电线路Kj-1Kj支路之间，同理分析可得故障点F到始端M1和终端Mn的故障距离与上述式（6）和（7）相同。

综上所述，对风电场中任意点故障，利用式（6）和式（7）计算出dM1F和dMnF，并根据已知线路长度dM1Mi、dMnMi和式（1）计算出各条风机支路的决策系数。

1.3 基于决策系数的故障支路判据

为说明基于决策系数的故障支路判据的有效性，在图2所示的海上风电场集电线路模型中进行阐述。将主集电线路M1M7当作由支路M1K1、K1K2、K2K3、K3K4、K4K5和K5M7组成的特殊支路。

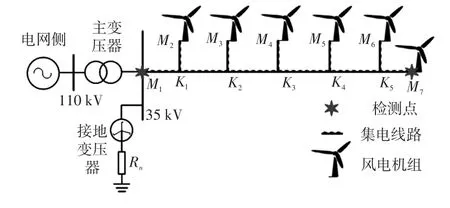
图2 海上风电场集电线路模型Fig.2 Collector line model of offshore wind farm

故障发生后，计算各条风机支路的决策系数。表1展示了故障发生在风机支路时各支路的决策系数。定义由始端M1到终端M7为正方向，根据表1结果可知，故障支路的决策系数为0，剩余支路的决策系数不为0；以故障风机支路为参考点，沿着正方向靠近始端M1支路的决策系数大于0，靠近终端M7支路的决策系数小于0。

表1 风机支路故障各风机支路决策系数Tab.1 Decision coefficient of each wind branch under wind branch fault

从表2结果可知，故障发生在主集电线路时，各条风机支路的决策系数全不为0，其数值与故障点位置有关。沿着正方向靠近始端M1风机支路的决策系数大于0，靠近终端M7风机支路的决策系数小于0。

表2 主集电线路故障各风机支路决策系数Tab.2 Decision coefficient of each wind branch under main collection line fault

在实际系统中，考虑到测量误差和计算误差，通过设置裕度ε对决策系数L进行修正，其修正原则为：当决策系数在裕度ε内，将L修正为0，否则保持不变。综上所述，海上风电场集电多分支线路故障区段判据如下：

（1）若风机支路的决策系数全不为0，则故障发生在主集电线路；若相邻的两条风机支路的决策系数符号相反，则故障发生在两条风机支路之间主集电线路部分；

（2）若某条风机支路的决策系数为0，其余风机支路的决策系数不为0，则说明故障发生在该条风机支路（风机支路较短，无需故障点定位）。

2 主集电线路故障点定位

2.1 故障行波波头标定

在集电线系统中任意点发生故障，故障点产生的故障行波信号将向各条线路的终端传播。通过模态分解可以滤除低频信号和噪声信号，减小信号干扰。ESMD是一种完全自适应的非线性信号处理方法，可以解得出模态信号的瞬时频率与幅值，实现不同频段信号的分离。设故障行波信号为f（t），ESMD具体分解流程如图3所示。线路发生故障后，通ESMD分解将故障行波信号分解为不同频段的模态信号IMFi（t）和分解余量R（t）。

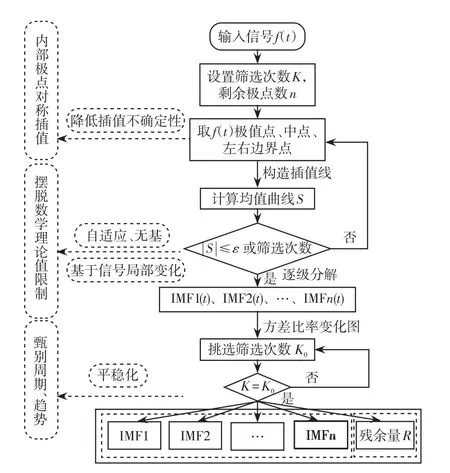
图3 ESMD算法流程Fig.3 Flow chart of ESMD algorithm

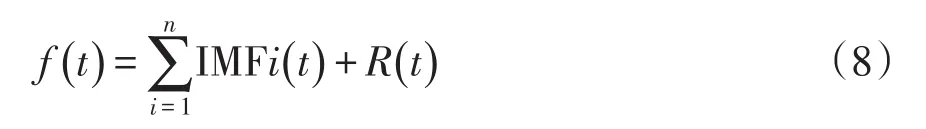
针对故障行波波头标定中暂态故障特征不明显导致波头难以识别的问题，本文通过Teager能量算子对分解后的一阶模态信号IMF1（t）进行差分运算，利用其能量集聚性增强暂态信号故障特征。本采用离散型Teager能量算子对故障行波信号进行波头标定，并通过式（9）差分运算得出Teager能量曲线，将首个峰值作为初始故障行波暂态波头的到达时刻。

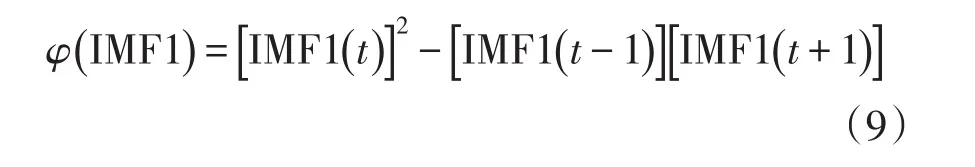
2.2 故障点定位

海上风电场集电线路故障定位流程如图4所示。考虑到行波定位方案的经济性和可行性，本文在仅主干线路末端设置检测点的情况下进行研究。由于风电场网络结构的复杂性，根据式（6）计算出的故障距离可能对应多个故障位置。因此，基于决策系数故障区段判定故障支路发生在主集电线路后，根据双端行波定位法实现故障点定位，利用式（10）计算出故障点到参考端M1和M7的距离。值得说明的是本文针对主集电线路故障实现故障点定位；针对风机支路故障，由于风机支路较短；仅实现故障区段定位。

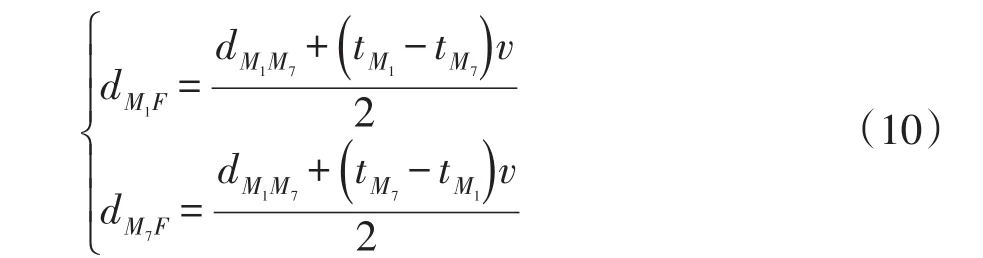
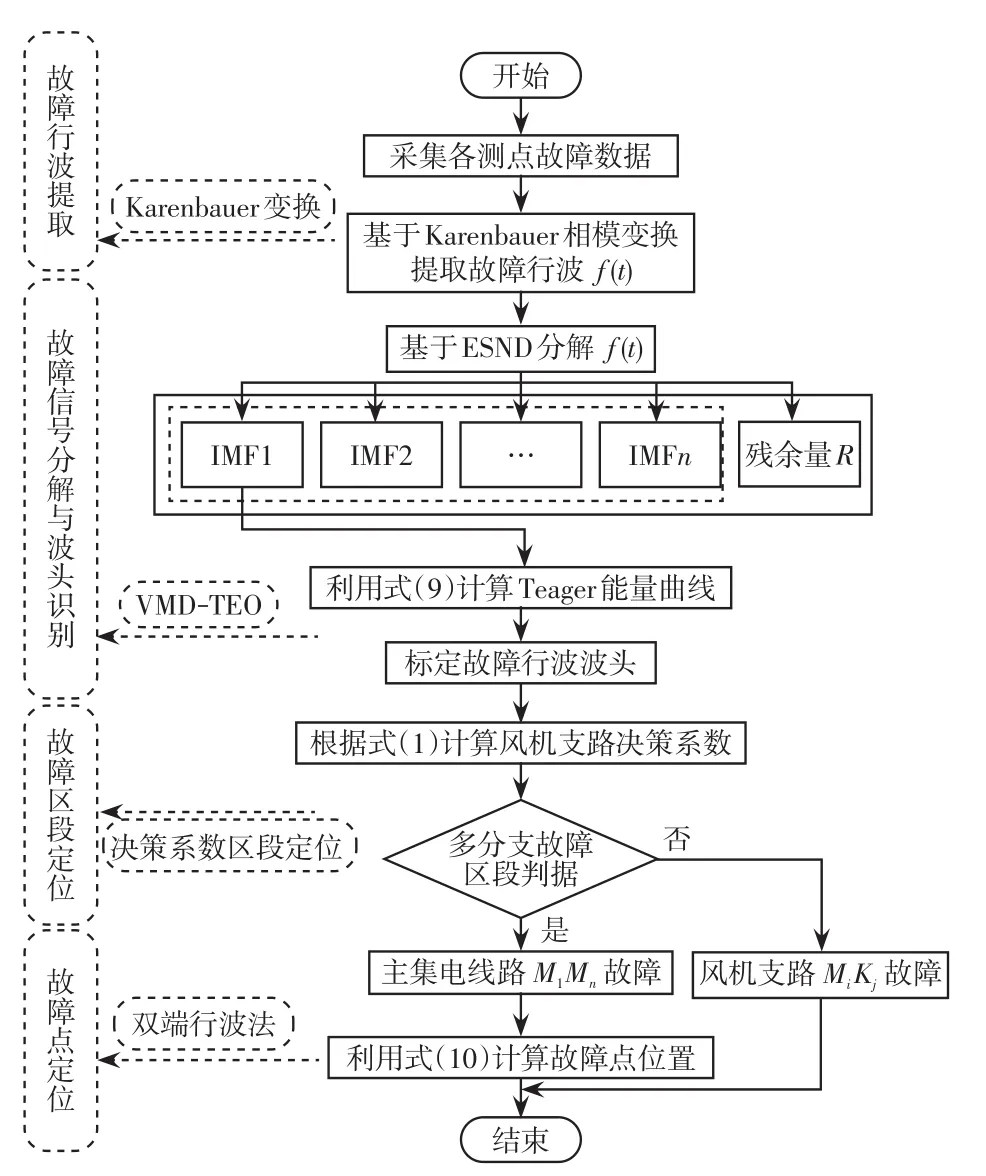
图4 海上风电场集电线路故障定位流程Fig.4 Flow chart of fault location of collector line in offshore wind farm

3 算例分析

为验证所提故障区段定位和故障点定位算法的有效性，参照图2搭建风电场集电线路模型。其中，线路 M1K1、K1K2、K2K3、K3K4、K4K5长度分别为2 km，M2K1、M3K2、M4K3、M5K4、M6K5、K5M7分别为0.6 km；其正序参数为L=9.337×10-4H/km，C=1.274×10-8F/km。在线路端M1和M7处采集故障数据。在仿真中，将故障点分别设置在线路的不同位置，采样频率为1 MHz，利用ESMD-TEO标定线模、零模分量故障行波波头。与高压输电线路相比，分支线路长度较短，可认为波速稳定不变，本文基于计算故障行波在线路中传播速度为2.899×105km/s。

3.1 故障区段定位分析

为验证所提基于决策系数的故障区段定位算法准确性，在主集电线路K1K2距离检测点M1端3.4 km处，设置故障起始角为20°，过渡电阻为20 Ω的A相接地故障。分别在测量点M1和M7提取故障行波，利用ESMD-TEO标定故障行波线模分量和零模分量达到M1和M7端的时间。检测结果如图5所示。

由图5可知，故障行波零模分量到达端M1和M7的时间分别为0.119 ms和0.141 ms；线模分量分别到达检测端M1和M7的时间分别为0.111 ms和0.124 ms。将识别的各模态故障行波波头的时间分别代入公式（6）和（7）计算出故障点到线路终端的距离dM1F和dM7F分别为3.350 km和7.119 km。

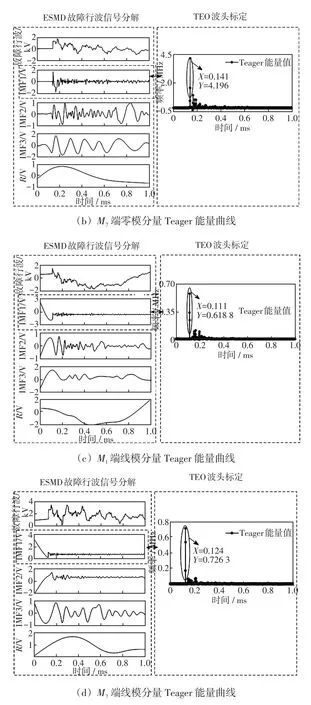
图5 K1K2故障时行波模态分量Fig.5 Mode components of traveling wave under fault K1K2

根据计算出的dM1F、dM7F和线路固有拓扑线路长度，并基于式（1）计算出风机支路M3K2故障时风机支路M2K1的决策系数为

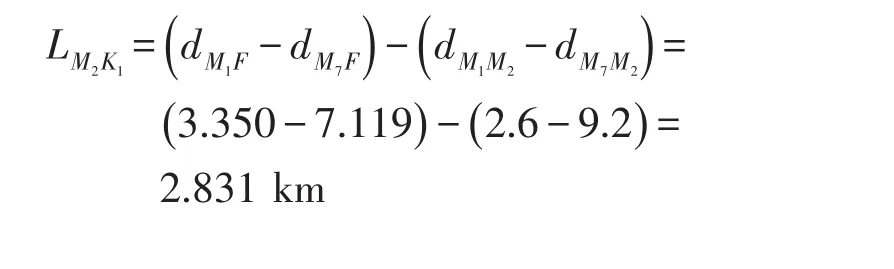
同理计算剩余风机支路的决策系数，结果如表3所示。表3结果表明，风机支路的决策系数都不为0，且支路M2K1和支路M3K2的决策系数符号相反，满足故障判据（1），判定故障发生在支路K1K2，与实际故障区段相符。

表3 支路K1K2故障各风机支路决策系数Tab.3 Decision coefficient of each wind branch under faultK1K2

在风机支路M3K2距离M3端0.3km处，设置故障起始角为30°，过渡电阻为10 Ω的AB相间故障。同理，通过ESMD-TEO标定出故障行波零模分量到达检测端M1和M7的时间为0.123 ms和0.138 ms；线模分量到达时间为0.113 ms和0.122 ms。并根据上述结果计算得出dM1F和dM7F分别为4.349 km、6.958 km，支路M3K2的决策系数为-0.009 km。取修正裕度ε为-0.05 km≤ε≤0.05 km，可以将支路M3K2的决策系数修正为0。根据表4结果可知，支路M3K2的决策系数为0，其余风机支路的决策系数不为0，判定故障发生在支路M3K2，与实际故障区段相符。

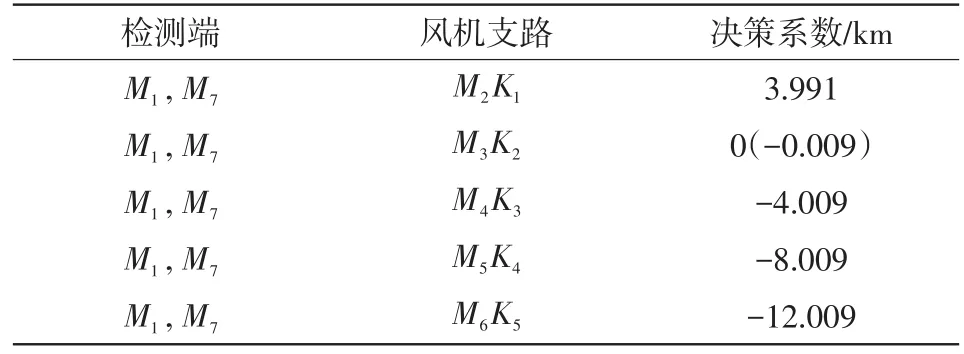
表4 支路M3K2故障各风机支路决策系数Tab.4 Decision coefficient of each wind branch under faultM3K2

为测试不同故障类型、故障起始角、过渡电阻和故障距离对所提故障区段识别方法的影响，按照表5所示的故障条件，分别在主集电线路M1M7，风机支路M2K1、M3K2、M4K3、M5K4、M6K5上模拟200组故障，模拟故障总数为1 200组。利用所提方法进行故障区段定位，由表6结果可知：基于决策系数的故障区段定位方法基本不受故障类型、过渡电阻、故障距离等因素的影响，且区段定位最低准确率在95%以上。

表5 故障初始条件Tab.5 Initial fault conditions

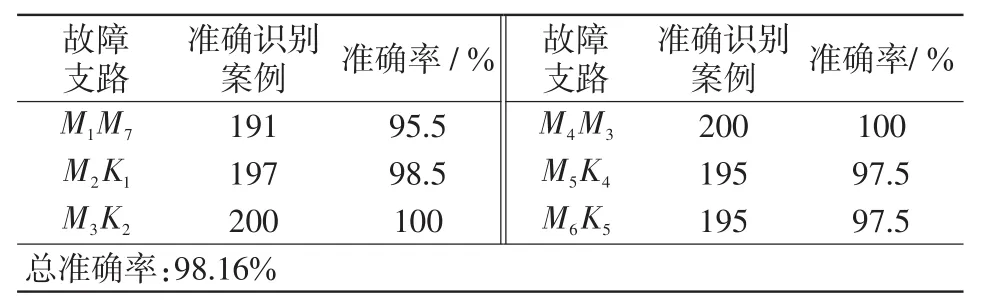
表6 各支路故障区段定位准确率Tab.6 Location accuracy of fault section in each branch

3.2 故障点定位分析

考虑到故障类型、故障距离、过渡电阻、故障起始角对定位结果的影响，分别在主集电线路的不同位置仿真不同类型故障。为比较所提ESMD-TEO算法的故障定位效果，与文献[4]所提出的小波变换模极大值WTMM（wavelet transform modulus maxima）分析方法在相同故障条件进行仿真对比。

1）不同故障距离的影响

为验证不同故障距离对定位精度的影响，分别在距M1端0.4 km、1.2 km、2.3 km、3.6 km、4.7 km、5.8 km、6.3 km、7.7 km、8.4 km、9.2 km、10.1 km处设置过渡电阻为20 Ω、故障起始角20°的AB相间故障。ESMD-TEO和WTMM两种方法的仿真对比结果如图6所示。

根据图6结果可知，在主集电线路不同位置发生故障时，本文所提的方法与WTMM方法都能定位到故障点，而ESMD-TEO的最大绝对误差为131.3 m，平均误差为48.9 m；WTMM最大绝对误差分别为188.9 m，平均误差为110.4 m。因此，ESMDTEO算法的定位精度受故障距离的影响更小，平均误差减小了61.5 m。

图6 不同故障距离测试结果Fig.6 Test results at different fault distances

2）不同过渡电阻的影响

为验证该算法在不同过渡电阻Rf下的性能，在距离M1端3.7 km处分别设置Rf为10 Ω、50 Ω、80 Ω、150 Ω、300 Ω，故障起始角为10°的AB相间故障。不同过渡电阻下的定位结果和绝对误差如表7所示。结果表明：两种算法的定位结果都不随Rf而显著变化，但ESMD-TEO最大绝对误差比WTMM更小。

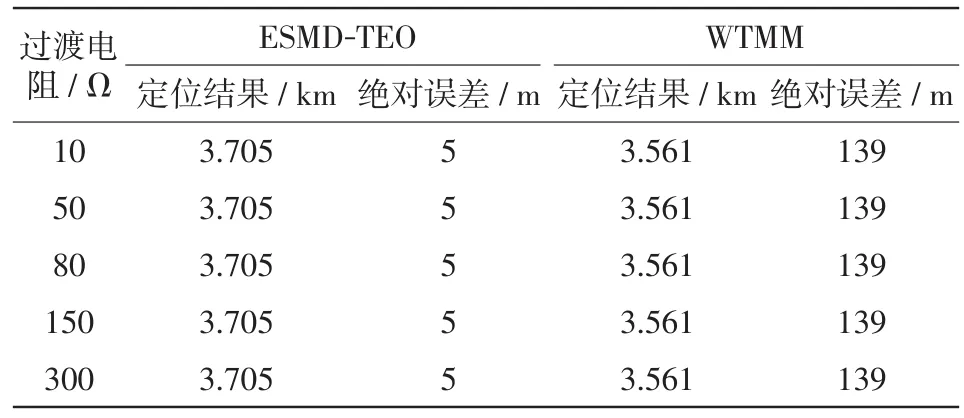
表7 不同过渡电阻测试结果Tab.7 Test results with different transition resistances

3）不同故障类型的影响

在距离M1端4.5 km处，过渡电阻为20 Ω、故障起始角为10°的情况下设置不同类型的故障。表8结果表明，ESMD-TEO和WTMM方法的定位结果都基本不受故障类型的影响，但相对而言ESMD-TEO具有更高的定位精度。

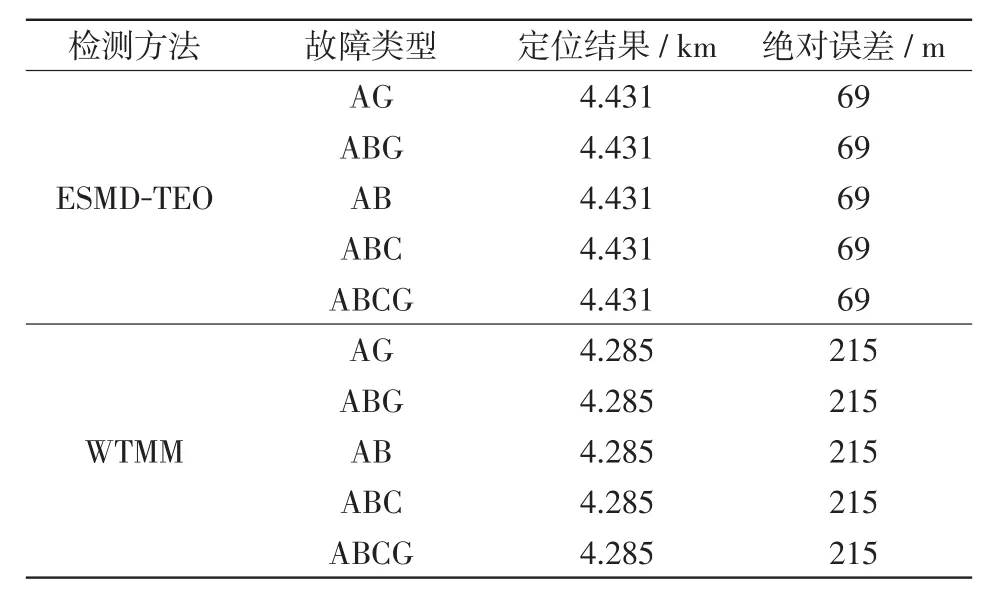
表8 不同故障类型测试结果Tab.8 Test results under different types of fault

4）不同故障起始角的影响

在距离M1端6.7 km处，过渡电阻为20 Ω、发生A相接地故障。故障起始角分别为20°、30°、45°、60°、80°时的测试结果如表8所示。根据表8结果可知，ESMD-TEO和WTMM方法都基本故障起始角的影响，但WTMM在故障起始角较小时定位误差较大。

综上分析，本文所提方法能够准确的辨别故障区段并计算出故障距离，且ESMD-TEO算法对故障起始角、故障类型和过渡电阻具有更强的鲁棒性，适用于海上风电场集电线路故障定位。

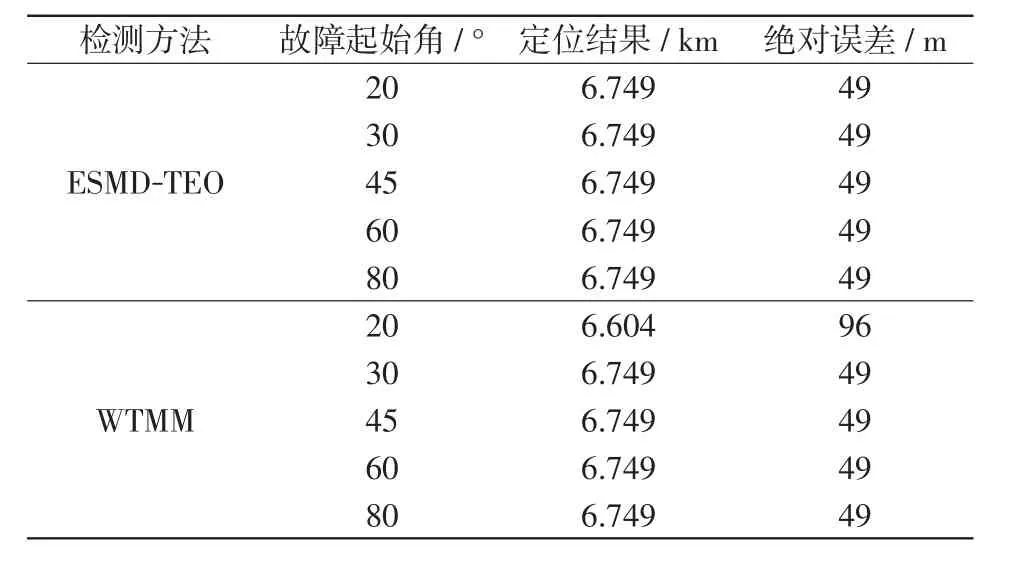
表9 不同故障起始角测试结果Tab.9 Test results at different fault inception angles

4 结论

本文针对海上风电场多分支线路故障区段定位和主集电线路故障点定位展开研究，主要结论如下。

（1）在不采集所有分支线路终端故障数据的情况下，通过分析故障点到各端点的距离和线路固有长度的关系构建决策系数函数，并基于决策系数与故障点位置之间的映射，提出相对应故障区段的定位判据，实现集电多分支线路故障区段的准确定位，解决了分支结构复杂对故障区段定位的影响。

（2）通过ESMD分解故障行波信号，滤除信号中的低频分量和噪声。利用TEO差分运算使一阶IMF信号幅值突变特征更加明显，实现故障初始行波波头的准确标定，有效地提高故障定位精度。

（3）仿真结果表明，所提方法能准确地定位出故障支路并准确计算出故障点位置。与WTMM算法相比，平均绝对误差减小了61.5 m，且定位结果基本不受故障距离、过渡电阻等因素的影响，鲁棒性更强。