抗干扰算法改进的发电机转子接地保护

朱宇聪，王树刚，桑建斌，包明磊，李玉平，陈福锋

（1. 国电南京自动化股份有限公司，江苏 南京 211100；2. 南京国电南自电网自动化有限公司，江苏 南京 211100；3. 国网江苏省电力有限公司，江苏 南京 210024）

0 引言

发电机转子回路一点接地故障是发电机转子绕组绝缘破坏常见的故障形式，因此需要配置可靠的转子接地保护［1］。目前乒乓式转子接地保护［2-3］和注入式转子接地保护［4-6］在现场应用最为广泛。

转子接地保护采用转子电压和漏电流等模拟量计算转子接地电阻和接地位置，实现转子接地保护功能，其中漏电流易受干扰。为了减少误差，一般使用转子电压和漏电流等模拟量的平均值进行计算。转子绕组和轴电压阻容吸收回路的等效对地电容充放电过程［7］、测量回路受高次谐波［8］、分数谐波［9］和电磁干扰等影响，都可能导致转子接地保护误动作。

经过长期的运行实践，转子接地保护已经得到了较大的改进，但其精度和可靠性仍有待提升。文献［4，7，9］中通过调整电子开关的切换周期消除等效对地电容充放电的影响；文献［10］对转子电压Ur的变化率dUr/dt进行自动跟踪计算，当其不超过一个小的门槛值时，认为等效对地电容的充放电已完成，取之后的稳态数据用于计算，从而消除等效对地电容充放电的影响。文献［9］通过调整直流量计算周期的大小，消除了因转子偏心产生的分数谐波对保护的影响，该方法值得借鉴。

目前大部分文献在测量转子接地电阻时均假设转子电压在切换周期内保持不变，部分文献提到切换周期内转子电压变化的情况，但未进行进一步分析研究；大部分文献对转子电压和漏电流固定取等效对地电容充放电过程结束后某个时刻的采样点，未考虑电容充放电过程结束后励磁调节和电磁干扰的影响。因此，本文提出了一种新型转子接地保护抗干扰算法，该算法主要采用软硬件滤波、漏电流采样值平均值之和值变化率比较和分段数据筛选的方法，实验验证结果显示该算法有效提高了转子接地保护的精度与可靠性。

1 转子接地保护原理简介

注入式转子接地保护原理为：在转子绕组的正、负两端（或负端）与大轴之间注入一个直流电压，根据电子开关的打开和闭合状态，实时求解电路回路方程得到转子接地电阻与接地位置。下面以双端注入式转子接地保护原理为例进行说明［4］，电路原理图如图1 所示。图中，α为转子接地位置；R为大功率电阻，其阻值为40 kΩ；E为50 V的注入直流电源；Rg为转子接地电阻；Ip、In分别为转子漏电流1、2；K为电子开关。

图1 双端注入式转子接地保护原理图Fig.1 Principle diagram of double-terminal injection rotor grounding protection

根据图1，得到K 打开、闭合状态下的回路方程分别如式（1）、（2）所示。

式中：ΔUs为电子开关的通态压降；上标“′”表示K 闭合状态下的变量。

根据式（1）、（2）得到Rg、α的计算公式为：

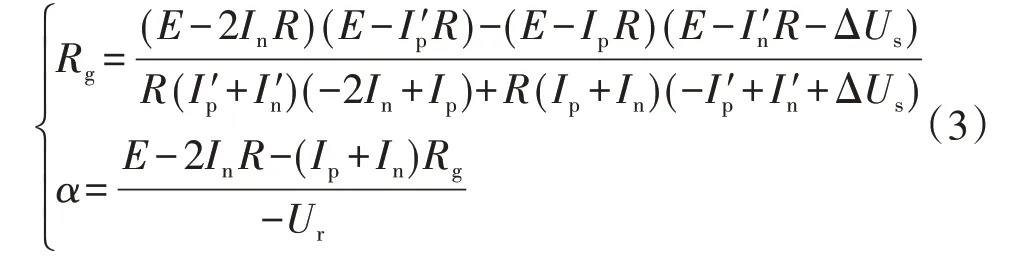
准确求取Rg、α的关键在于获取准确的转子电压和漏电流，后文将针对如何消除干扰信号影响进行详细介绍。

2 转子电压特征及测量回路内干扰信号

2.1 典型转子电压波形和谐波

在同步发电机励磁系统中，晶闸管整流电路将交流电压转换为直流电压，其中以三相桥式全控整流电路应用最为广泛。该电路产生的转子电压波形为锯齿状波形，一个周期（20 ms）内有6 个锯齿。图2 为三相桥式全控整流电路带阻感负载时的典型转子电压波形［11］。图中30°为脉冲角。

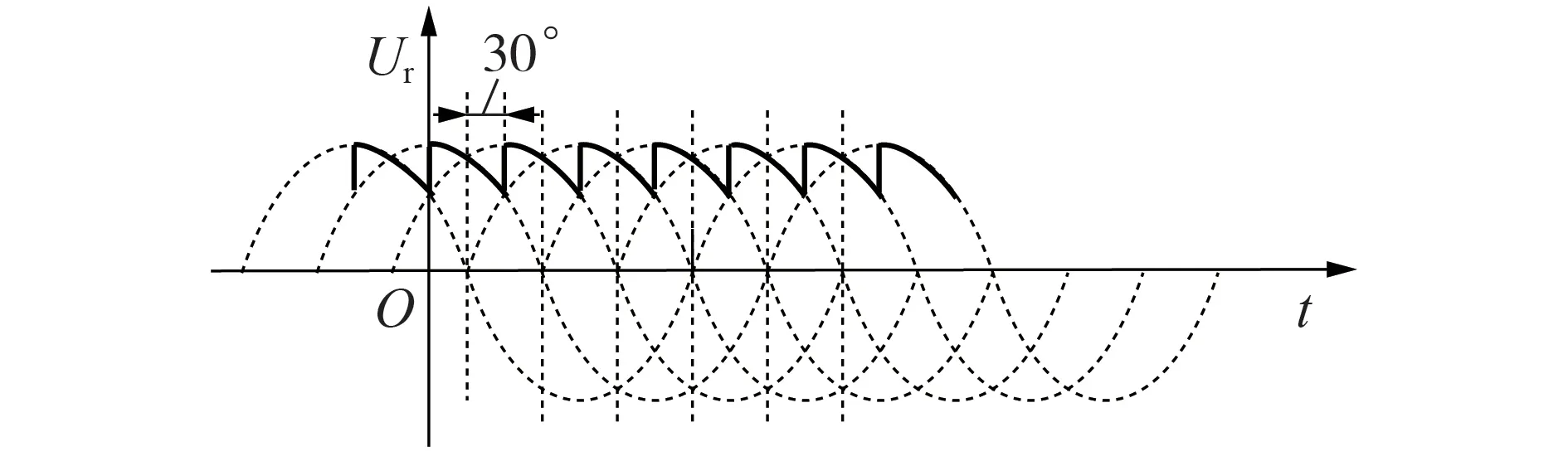
图2 三相桥式全控整流电路带阻感负载时的典型转子电压波形Fig.2 Typical waveform of rotor voltage generated by three-phase bridge full-controlled rectifier with resistive inductive load

晶闸管整流电路的输出电压是周期性的非正弦函数，其主要成分是直流，同时包含pk次特征谐波，其中p为脉动数，k=1，2，…。p=6 时，特征谐波幅值与脉冲角的关系如图3 所示。图中，U*rw为特征谐波幅值的标幺值；β为脉冲角。由图可见：随着谐波次数的增大，U*rw迅速减小；当β在0°～90°范围内变化时，U*rw随着β的增大而增大，β=90°时U*rw最大；当β在90°～180°范围内变化时电路工作于有源逆变状态，U*rw随着β的增大而减小［11］。

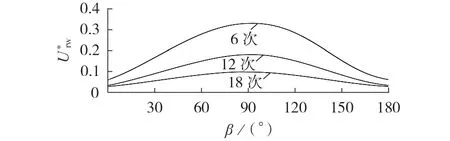
图3 特征谐波幅值与脉冲角的关系（p=6）Fig.3 Relationship between characteristic harmonic amplitude and pulse angle（p=6）

在电网中，波动负载、电弧类负载、静止变频装置、感应电动机、整周波控制的晶闸管装置等均可能产生分数谐波，并通过电磁耦合传递到转子绕组中。此外，发电机转子绕组偏心故障严重时，部分气隙变宽，部分气隙变窄，发电机气隙磁场将发生畸变，转子绕组中将产生幅值较大的分数谐波［9］。可见转子电压在1 个周期内是波动变化的，且转子绕组的高次和分数谐波不容忽略，因此应对转子电压和漏电流采取低通滤波处理。

2.2 测量回路内干扰信号

大型发电机的转子绕组本身的等效对地电容最大为1～2 μF［1］，大型汽轮发电机通常采用静止励磁系统，为了抑制轴电压的幅值，通常装设如图4 所示的专用轴电压阻容吸收回路。图中，r为电阻；C为电容。国内外的励磁系统的阻容吸收回路各不相同，一般电阻值较小，电容值为2～10 μF不等［7，12］。

图4 阻容吸收回路示意图Fig.4 Schematic diagram of RC absorption circuit

转子接地保护测量电路和阻容吸收回路共同组成的等效电路如图5（a）所示，从ab 端口进行二端口网络等效可以得到简化等效电路如图5（b）所示。图中，U′为转子电压的等效电压源；i（t）为注入直流电源E所在支路的等效电流；∑R、∑C分别为电路等效总电阻、总电容。时间常数τ=∑R∑C，约3τ～4τ的时间后，电容充放电过程完成。转子绕组等效对地总电容越大，其充放电暂态过程越长，将影响转子接地保护的精度和可靠性。

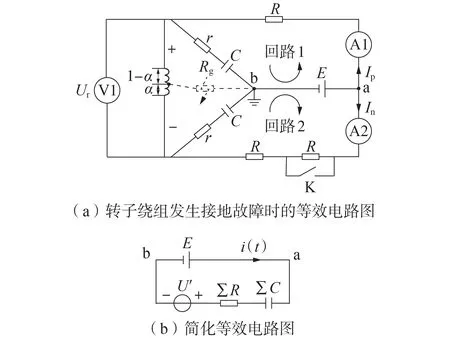
图5 转子接地测量回路和阻容吸收回路共同组成的等效电路及其简化电路Fig.5 Equivalent circuit composed of rotor grounding measurement circuit and RC absorption circuit and its simplified circuit

此外，受励磁系统调节、电磁干扰等的影响，转子接地测量回路的转子电压和漏电流可能会发生剧烈波动，从而影响转子接地保护的精度和可靠性，因此算法需要消除干扰信号的影响。

3 转子接地保护直流量抗干扰算法

3.1 抗干扰算法流程图

本文所提转子接地保护直流量抗干扰算法的流程图如图6所示。

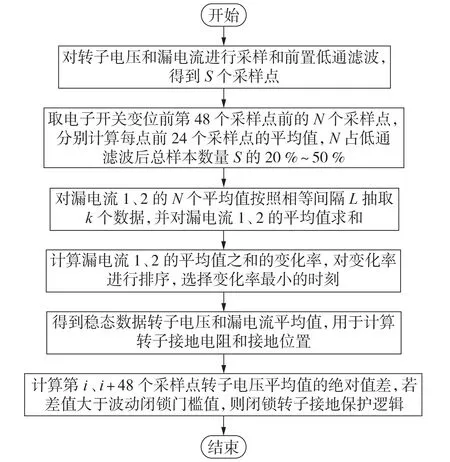
图6 抗干扰算法流程图Fig.6 Flowchart of anti-interference algorithm

3.2 低通滤波处理

保护装置同时采用硬件和软件方式对转子电压和漏电流进行低通滤波处理，滤除转子绕组中的高次和分数谐波。

软件低通滤波器为非递归数字低通滤波器，其幅频特性如图7所示。由图7可见，软件低通滤波器截止频率为10 Hz 左右，对于50 Hz 及以上谐波的滤过比达到90。

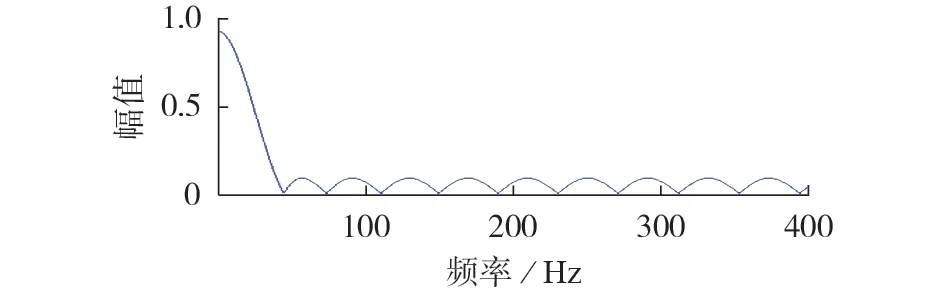
图7 软件低通滤波器的幅频特性Fig.7 Amplitude-frequency characteristic of software low-pass filter

软件低通滤波器的实现方式为：

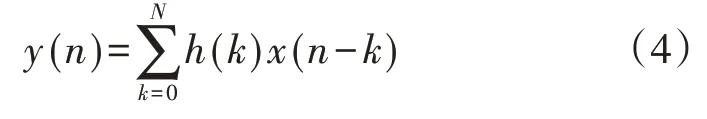
式中：x(n)为当前采样点；h(k)为滤波器系数，其数量为N+1；y(n)为滤波后的采样点。

3.3 第一次数据选择

第一次数据选择主要是消除等效对地电容充放电暂态过程的影响。在电子开关K 打开状态下，分别获取S个采样点的转子电压与漏电流，S值由电子开关K 的切换周期T和保护装置采样频率fs共同决定，设置S=0.5T fs。对于含有轴电压阻容吸收回路的大型汽轮发电机组，由于其等效对地电容较大，电容充放电暂态过程较长，需要根据现场实际情况增大电子开关K的切换周期T。

第一次数据选择示意图如图8 所示。图中，SK为电子开关状态，其值为1、0 分别表示电子开关打开和闭合。该数据序列包括N个采样点，N在0.2S～0.5S范围内自动取值。为了防止电子开关状态信号延迟，导致采样序列跨越2 个状态，图中选取电子开关变位前第48个采样点之前的采样序列。

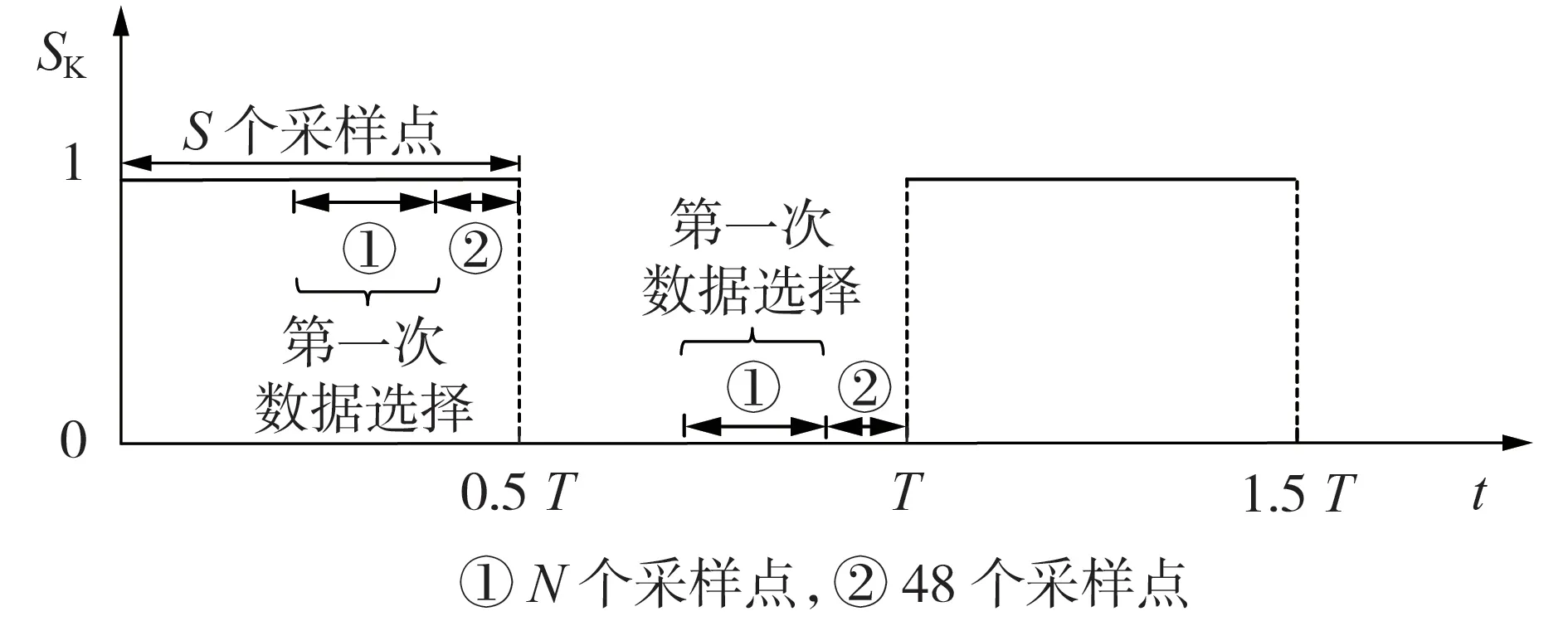
图8 第一次数据选择示意图Fig.8 Schematic diagram of first data selection

记每次电子开关变位前第48 个采样点对应时刻为当前时刻，ip(n)、in(n)、ur(n)分别为当前时刻的漏电流1采样值、漏电流2采样值、转子电压采样值，ip(n+i)、in(n+i)、ur(n+i)分别为当前时刻前的第i个采样点的漏电流1 采样值、漏电流2 采样值、转子电压采样值，装置采用逆序存储方式，存储数据包括采样点以及每个采样时刻对应的平均值，当前时刻前第i个采样点的平均值计算公式如下：

第一次数据选取方式有效地避开了转子绕组等效对地电容的充放电过程，减小了电子开关位置状态延迟的影响。

3.4 第二次数据选择

第二次数据选择主要是消除励磁系统调节和电磁干扰的影响，采用的方法为对包含N个平均值的数据序列进行的分段筛选，查找漏电流和值变化率最小时刻的数据，主要步骤如下。

1）将漏电流1、2采样值的N个平均值分成k组，每组包含L个数据，按照相等的间隔L抽取k个数据，并对漏电流1、2 采样值的平均值求和，形成新的数据序列，即：

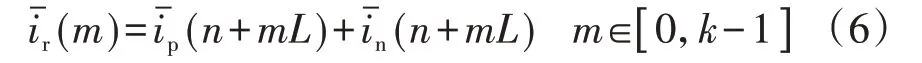
式中：N=kL且L＞24。

通常在转子绕组对地绝缘良好的情况下，漏电流1 与2 幅值相等、方向相反，则漏电流1、2 的和值为0；当转子绕组对大轴绝缘降低，漏电流和值大于启动门槛时，程序才计算Rg，这样处理能够有效减少共模干扰影响。

转子绕组对大轴绝缘降低时，漏电流1、2 采样值的平均值之和增大，程序开始计算Rg；当受干扰信号影响时，漏电流1、2 的采样值的平均值之和会发生剧烈的变化；当干扰信号消失后漏电流1、2 的采样值的平均值之和变化趋于平缓。所以按照采样值的平均值之和最小选取数据，能有效地避开间歇性的干扰信号。

4）依据步骤3）得到的M值，得到K 打开状态下稳态数据漏电流1、2 的平均值和转子电压平均值为：

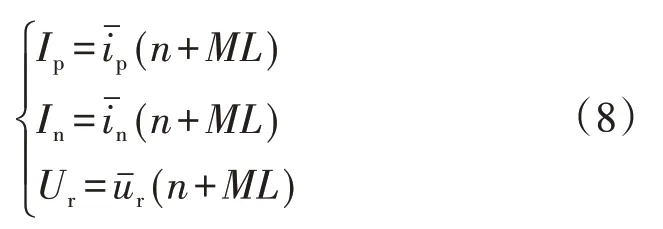
同理得到K 闭合状态下稳态数据漏电流平均值I′p、I′n，将Ip、In、Ur、I′p、I′n代入式（3）计算得到Rg和α。

3.5 转子电压剧烈波动闭锁

当转子电压和漏电流在整个数据窗内都剧烈波动，前文所述的2 次数据选择无法选出波动较小的数据窗时，判断转子电压波动过大，闭锁转子接地保护的逻辑判断，延时t1（t1∈［3T，10T］）后返回。转子电压波动过大的判据为：

4 抗干扰算法的试验验证

4.1 静模试验验证

保护装置采用ZYNQ 高性能双核处理器，装置的采样频率fs=1 200 Hz，投入的保护类型为双端注入式转子接地保护。本文中，进行静模测试时将转子绕组视为直流电压源，采用PW466 测试仪输出的直流电压叠加交流电压来模拟转子电压，仅模拟转子绕组正端或负端接地故障，设置电子开关K 切换周期T=1 s。

1）静模试验1：转子绕组负端分别经5、20 kΩ 电阻接地，测试仪输出60～170 V 剧烈波动的直流电压。图9为静模试验1的结果。图中，Rgc1和Rgc2为Rg的测量值。Rgc1的测量方式为：采用式（3）进行测量，且式（3）中转子电压和漏电流采用经本文算法处理后的平均值。为方便对比接地电阻的测量效果，Rgc2的测量方式为：采用式（3）进行测量，但式（3）中转子电压和漏电流未经本文算法处理，固定取电子开关变位前第48个采样点的24点平均值。下文中的Rgc1和Rgc2均采用上述测量方式。

由图9可见：转子绕组负端经5 kΩ电阻接地时，Rgc1为4.55～5.38 kΩ，Rgc2为4.12～4.96 kΩ；经20 kΩ 电阻接地时，Rgc1为19.0～20.5 kΩ，Rgc2为18.05～35.64 kΩ；Rgc1的数值虽然存在一定的波动，但仍然满足精度要求（0.5 kΩ 或±10%）［13］，而Rgc2的数值精度相对较差。

2）静模试验2：转子绕组负端分别经5、20 kΩ 电阻接地，测试仪输出30 V（30 Hz）的交流电压叠加在转子绕组上，保护装置自身产生50 V 直流电压源。静模试验2的结果如图10所示。由图可见：软、硬件低通滤波器对30 Hz 分数谐波的滤除特性较强，可有效减小转子电压和漏电流的波动幅值；转子绕组负端经5 kΩ 电阻接地时，Rgc1为4.99～5.05 kΩ，Rgc2为4.40～5.04 kΩ；转子绕组负端经20 kΩ 电阻接地时，Rgc1为18.94～20.44 kΩ，Rgc2为16.00～24.82 kΩ；可见Rgc1的精度更高，满足精度要求。

3）静模试验3：转子绕组负端经5、20 kΩ 电阻接地，测试仪输出30 V（10 Hz）交流电压叠加在转子绕组上。静模试验3的结果如图11所示。从图中可见：相对30 Hz分数谐波，软、硬件低通滤波器对10 Hz分数谐波的滤除特性较弱；转子绕组负端经5 kΩ 电阻接地时，Rgc1为3.82～4.82 kΩ，Rgc2为0～6.03 kΩ；转子绕组负端经20 kΩ电阻接地时，Rgc1为18.4～19.75 kΩ，Rgc2为17.91～27.44 kΩ；可见在静模试验3 中，Rgc1的精度仍然更好。

图11 静模试验3的结果Fig.11 Results of Static Test 3

4.2 电磁兼容试验验证

电磁兼容（EMC）试验采用PEFT4010 快速瞬变试验仪器输出干扰信号；干扰信号试验电平为±4.4 kV，重复频率为4 kHz［14］，持续时间为正、负极性各60 s。EMC 试验接线如图12 所示。试验方法为：保护装置处于正常工作状态，电子开关K切换周期T=1.2 s，通过PW466 试验仪输出转子电压，试验时PEFT4010输出干扰信号，通过共性耦合夹将干扰信号分别加到转子绕组正、负端端子。

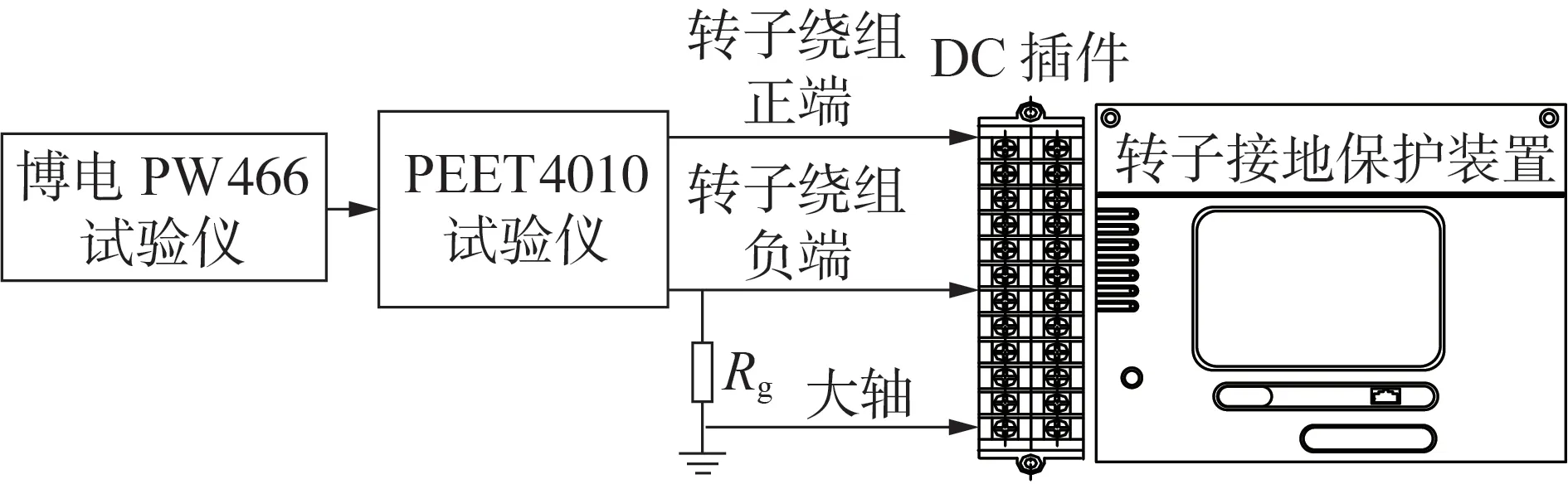
图12 EMC试验接线图Fig.12 Wiring diagram of EMC test

EMC 试验结果如图13所示。由图可见：转子绕组负端经5 kΩ 电阻接地时，Rgc1为4.98～5.05 kΩ，Rgc2为4.41～5.06 kΩ；经转子绕组负端经20 kΩ 电阻接地时Rgc1为19.87～20.02 kΩ，Rgc2为19.61～43.88 kΩ，Rgc1精度较好，利用本文算法可有效避开干扰信号；当快瞬干扰信号发生在Rgc2采用的固定数据窗内时，Rgc2的数值波动很大，超出精度要求范围，精度受干扰信号影响较大。

图13 EMC试验结果Fig.13 Results of EMC test

4.3 动模试验验证

本节采用动模故障波形回放方式对算法进行验证，动模机组主回路接线如图14所示。

图14 动模试验主回路Fig.14 Main circuit of dynamic test

设置电子开关K切换周期T=1 s，转子绕组负端分别经5、20 kΩ 电阻接地。在物理动模环境下设置发变组高压侧发生金属性故障，通过测试仪器回放转子电压波形，如图15 所示。当发变组高压侧发生接地故障时，为了维持机端电压稳定，励磁系统强励调节，转子电压迅速增加至160 V，故障消失后，转子电压逐渐恢复正常。从图中可知：转子绕组负端经5 kΩ 电阻接地时，Rgc1为4.74～5.26 kΩ，Rgc2为4.72～5.15 kΩ；转子绕组负端经20 kΩ 电阻接地时，Rgc1为19.60～20.57 kΩ，Rgc2为19.18～20.17 kΩ，励磁系统强励调节只影响2～3 个切换周期，Rgc1和Rgc2均满足精度要求。

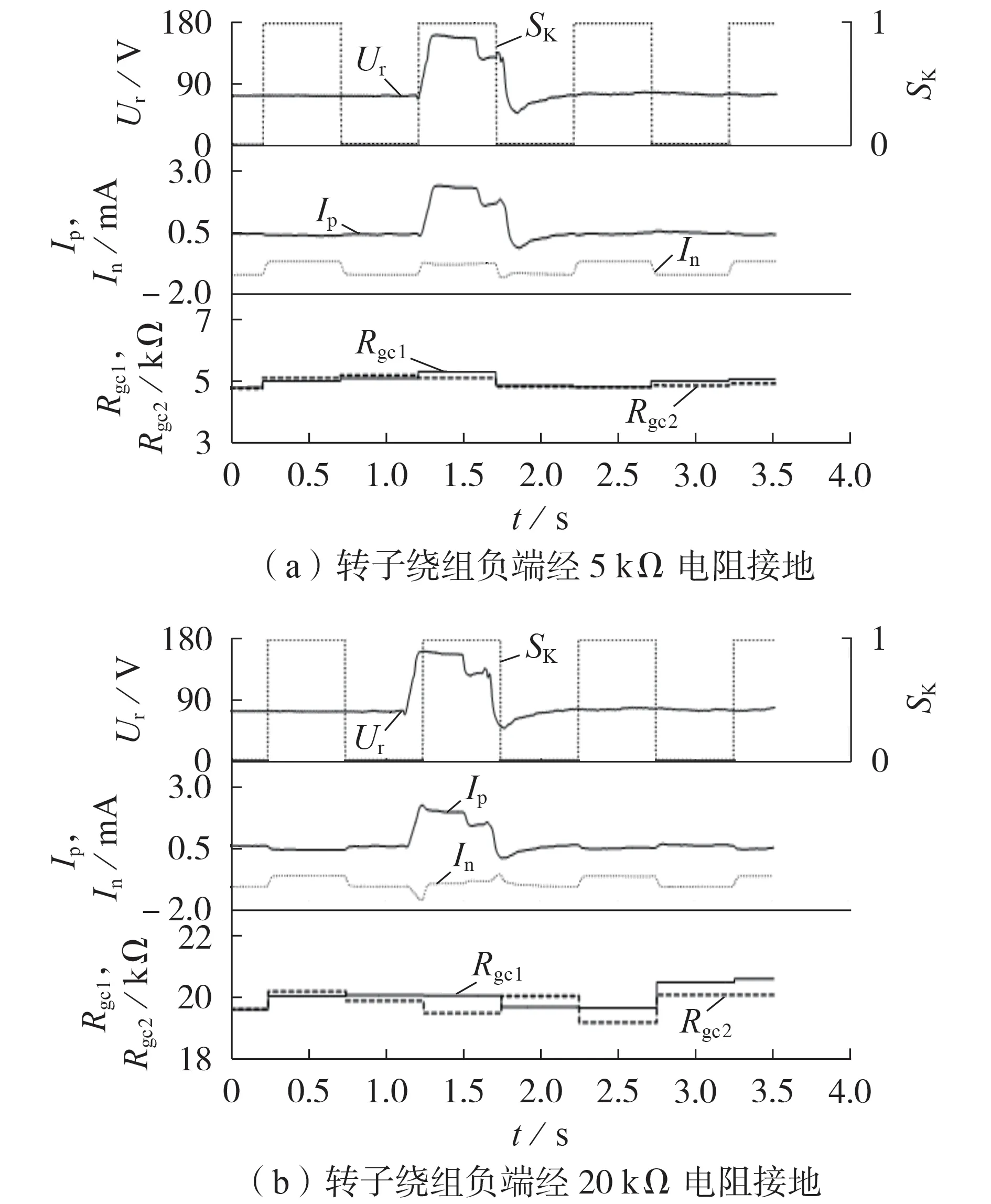
图15 动模试验结果Fig.15 Results of dynamic test

综上可知：当转子绕组发生接地故障时，采用新抗干扰算法的转子接地保护在转子电压叠加高次谐波和分数谐波时，接地电阻的测量精度较高，且满足精度范围要求；在受励磁调节和电磁干扰影响导致转子电压剧烈波动时，保护的动态测量精度同样较好。

5 结论

本文分析了发电机转子绕组中存在的干扰信号，提出了一种转子接地保护抗干扰算法。本文算法考虑了励磁系统调节、谐波、非周期分量、电磁干扰等对转子接地保护的影响，并在保护装置上进行了试验验证。本文通过理论分析及试验验证得到以下结论：

1）本文根据电子开关位置、切换周期、漏电流采样值平均值的和值变化率等，选取出波动较小和干扰较小的转子电压和漏电流稳态数据，有效提高了转子接地电阻的测量精度与可靠性；

2）本文要求在转子接地测量周期内存在不含干扰信号的时间窗口，对于全测量周期内都充斥着干扰信号的情况并不能保证精度，针对此情况提出了转子电压剧烈波动闭锁判据，闭锁保护装置逻辑计算；

3）本文以双端注入式转子接地保护为例介绍所提抗干扰算法，该算法同样适用于乒乓式和单端注入式转子接地保护。