换相电压负序分量对LCC-HVDC输电系统换相的影响分析及其抑制策略

刘 对，李晓华，蔡泽祥，殷珊珊

（华南理工大学 电力学院，广东 广州 510640）

0 引言

传统的基于电网换相换流器的高压直流（LCCHVDC）输电系统因具有建设成本相对低、传输容量大、功率调节灵活等优点在电网中得到了大规模应用［1］。然而晶闸管器件的半控特性及LCC-HVDC 输电系统的正常运行以基波正序换相电压为前提进行分析，这就使得换相失败、多次换相失败可能会在逆变侧交流系统发生故障时出现。此时系统中的电气量会发生剧烈的变化，这将对交直流混联电网的安全稳定运行提出巨大挑战［2］。

目前，国内外学者针对LCC-HVDC 输电系统换相失败方面的问题做了大量的研究。针对多次换相失败机理研究，文献［3］运用谐波电压-时间面积方法来分析LCC-HVDC 输电系统多次换相失败机理，发现导致后续换相失败的主要原因是故障恢复期间的谐波，然而文中并没有给出相应的抑制措施。文献［4］以我国某特高压主变充电为例，说明了励磁涌流导致换流母线畸变从而导致周期性换相失败，但发生故障与励磁涌流所引起的谐波特性存在一定差异。文献［5］通过分析证明，在不对称故障下系统的触发角会表现出周期性波动，从而引发多次换相失败；并在分析的基础上给出了相应的抑制措施，但没有分析对称故障下系统触发角对LCC-HVDC输电系统换相失败的影响。文献［6］从锁相环的角度出发，指出了传统的同步旋转坐标锁相环（SRF-PLL）在故障下存在的问题并提出抑制多次换相失败的方法，但并未给出故障过程中锁相环受影响的理论分析。

针对换相失败抑制问题，文献［7］采用换相失败预测控制来抑制LCC-HVDC 输电系统的换相失败，然而需要快速地检测电压幅值以及零序分量以实现该抑制效果。文献［8］提出采用交流量来启动低压限流环节以达到换相失败抑制的作用，但在直流侧线路发生故障时该方法没有预想的优势。文献［9］通过分别在低压限流环节前增加虚拟电阻、电感来改进启动电压，对抑制多次换相失败有一定的效果，然而在故障恢复期间虚拟电阻、电感的存在导致恢复速度较慢。文献［10］从控制的层面进行改进，以减少换相失败的发生，但这些方法同样需要较高的检测速度。文献［11］提出采用虚拟换相面积缺乏量来确定电流的参考值，但该方法受延时条件制约。此外，换流器拓扑改造［12］、无功补偿装置［13］、改进电流偏差［14］等方法也可以抑制换相失败。虽然上述方法可以抑制换相失败，但锁相环的暂态性能对LCCHVDC 输电系统的影响研究较少。文献［15］从畸变电压对锁相环的影响出发分析了LCC-HVDC输电系统的运行特性，但在后续分析中认为锁相环锁定的仍是正序基波电压。

鉴于此，本文基于逆变侧交流系统故障下换相电压负序分量的分析结果，对LCC-HVDC 输电系统的锁相环进行改进。首先定量解析了换相电压负序分量对锁相环的影响；然后结合换相电压-时间面积方法定性分析了换相电压负序分量对LCC-HVDC输电系统换相的影响；最后提出了多次换相失败抑制策略的双二阶广义积分器锁相环（DSOGI-PLL）改进方法。该方法首先利用具有正、负序分离特性的相序解耦谐振（SDR）控制器，提取换相电压正序分量以减少后续低次谐波滤除的负担；然后采用双二阶广义积分-正交信号发生器（SOGI-QSG）对该正序电压再次分离并消除谐波；最后应用正交谐波消除模块（QHCM）滤除低次谐波，从而完成电网电压相位的快速、准确追踪。在LCC-HVDC 输电系统中应用该锁相环，通过PSCAD／EMTDC 仿真验证了所提改进DSOGI-PLL 的快速性与准确性。仿真结果表明，采用所提改进方法能够减少系统在故障持续期间发生换相失败的概率，可为多次换相失败的抑制提供参考。

1 换相电压负序分量对LCC-HVDC 输电系统的影响分析

传统电力系统中一般认为发生对称故障时不存在负序分量（或负序分量较小可以忽略），负序分量仅出现在不对称故障中。然而在LCC-HVDC输电系统中，由于控制系统的作用，在换流母线处发生对称故障时也将出现较大的换相电压负序分量。

1.1 换流母线不同故障下换相电压负序分量的对比

为了验证LCC-HVDC输电系统中逆变侧换流母线对称故障下同样会出现较大的换相电压负序分量，以文献［16］中的CIGRE HVDC 模型为例进行说明，分别在单相接地短路、三相短路、相间接地短路、相间短路故障下进行仿真验证。设故障发生时刻为第2 s，持续时间为0.5 s，接地短路故障和相间故障中的接地电感和相间电感均为0.9 H。不同故障下换流母线负序电压低次谐波分量U的分布情况见附录A图A1。

对比图A1 所示各故障下换流母线负序电压低次谐波分量可以发现，在LCC-HVDC 输电系统中即使发生对称故障，其U的含量也基本与发生不对称故障时相持平。同时由于LCC-HVDC输电系统的触发、控制以及保护系统大多以正序基波电压为基础进行设计，当系统发生故障时，控制系统的调节作用所产生的换相电压负序分量将导致系统再次出现不平衡量。因此，当交流系统发生故障时，应着重考虑换相电压负序分量对LCC-HVDC输电系统的影响。

1.2 换相电压负序分量对LCC-HVDC 输电系统锁相触发的影响分析

根据前文分析，逆变侧交流母线无论发生对称还是非对称故障，LCC-HVDC 输电系统换流母线中换相电压负序电压低次谐波含量均较高。这也表明此时系统的三相电压不平衡程度较高，下面将重点分析三相电压不平衡时对锁相环的影响。设三相不平衡电压ua、ub、uc为：

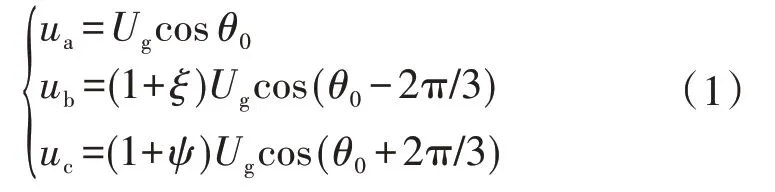
式中：Ug为电网电压幅值；ξ、ψ分别为b、c 相电压不平衡度；θ0为ua的初相位。根据Clark 变换，三相电压在α β坐标系下的表达式为：

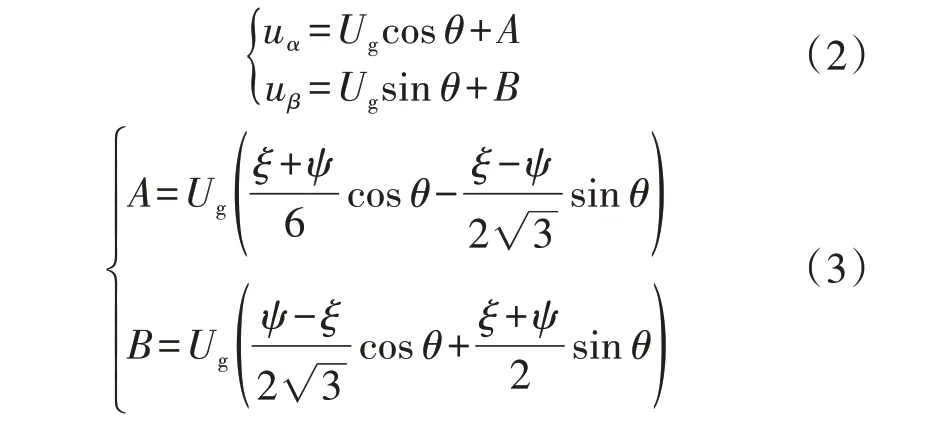
式中：θ为α轴超前a轴的夹角。由式（2）、（3）可知，A、B为三相电压不平衡量。同样根据Clark 变换，dq坐标系下三相电压q轴分量为：

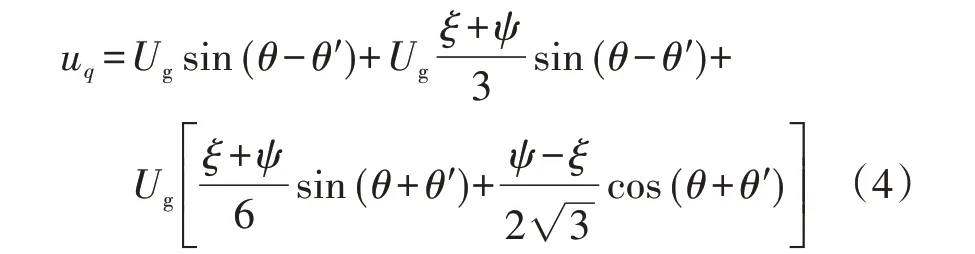
式中：θ′为d轴超前a轴的夹角。由于θ≈θ′，则uq所含有的误差Δe为：

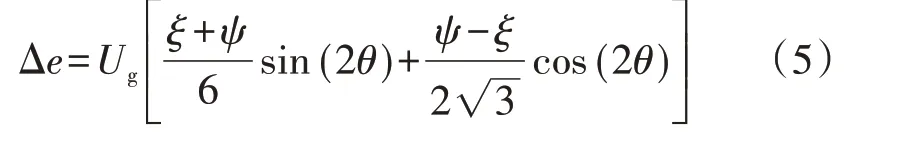
由式（5）可知：三相电压不平衡将引起一个2 倍频振荡的锁相误差；该误差也将影响锁相环的精度，从而影响LCC-HVDC输电系统的正常运行。

1.3 锁相触发对LCC-HVDC输电系统的影响分析

LCC-HVDC 输电系统一般采用12 脉动换流器，附录A 图A2 为CIGRE HVDC 模型中换流器接线图。CIGRE HVDC 模型中采用SRF-PLL 来跟踪换相电压的相位［16］；换流阀VY1—VY6、VD1—VD6按照VY1-VD1-VY2-VD2-…-VY6-VD6-VY1-VD1的顺序轮流导通，触发脉冲间隔为30°。

由图A2 可知，换流阀的换相过程是2 个换相电路中电感元件能量倒换的过程。因此，换相完成需要足够的电压-时间面积S0予以驱动。下面以VY4向VY6换相为例定性说明锁相触发对LCC-HVDC 输电系统的影响，其换相过程见附录A 图A3。故障后提前触发时刻tq、滞后触发时刻th提供的最大换相电压时间面积分别记为S′max、S″max，其表达式如式（6）所示。

式中：u′Yab为故障后换相电压；t3为故障后换相失败临界时刻。比较式（6）中的S′max、S″max与图A3 所示阴影部分S0可知，触发时刻与换相过程存在一定的关联，而触发时刻的准确与否受锁相环的影响。

由上述分析可知，故障情况下各触发脉冲发生器的输入信号将受到电压不平衡以及谐波的影响，影响LCC-HVDC 输电系统的正常换相，进而诱发换相失败［6］。研究发现，交流系统故障后LCC-HVDC输电系统的首次换相失败一般难以消除，但在故障未及时消除时，应该降低换相失败在LCC-HVDC 输电系统恢复过程中再次发生的概率［6］。然而，实际运行中的LCC-HVDC输电系统受换相电压负序分量以及谐波的影响较大。因此，实现快速、准确的锁相触发需首要考虑对换相电压负序分量以及谐波的处理。

2 改进的DSOGI-PLL

基于上述问题，本文提出一种可抑制LCC-HVDC输电系统多次换相失败的锁相方法。DSOGI-PLL具有一定滤波功能，故在谐波含量较少时，基波信息能够被有效提取。然而，当电压不对称或者谐波含量较高时，DSOGI-PLL 同样会受不对称度及谐波的影响，进而不能较准确地追踪同步信号。因此，DSOGI-PLL需要提升这方面的鲁棒性才能得以广泛应用。

2.1 SDR控制器

为了避免负序分量对锁相环的影响，正序分量的有效提取成为三相电压不平衡时需要解决的重要问题。由于SDR 控制器具有较好正、负序分量分离的特性，锁相环中可以借鉴这一特性进行设计［17］。SDR 控制器正、负序分量分离过程的传递函数GPSDR(s)、GNSDR(s)表达式如式（7）所示。

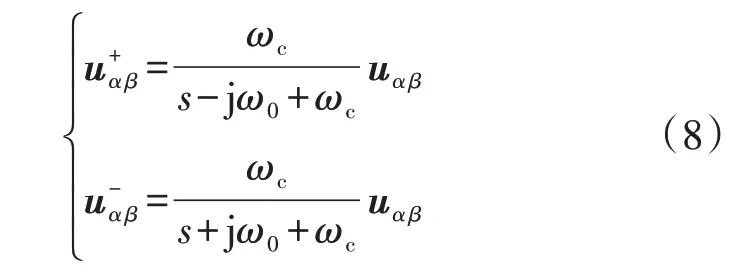
式中：uαβ=[uα uβ]为SDR 控制器在α β坐标系下的输入电压。当ω0=100 rad／s、ωc=150 rad／s 时，传递函数的伯德图如附录B 图B1 所示。由图可知，SDR 控制器本质上为谐振控制器，基波正序分量可以通过选取适当的ωc来提取。不同ωc（ωc分别为100、150、200 rad／s）下正序SDR 控制器伯德图如附录B 图B2 所示。对比图B2 中曲线可知，控制器的带宽、响应速度与参数ωc呈正相关，而增益衰减作用与参数ωc呈负相关。综合考虑本文的ωc取为100 rad／s。另外，通过对式（7）、（8）整理可得：

此时，正、负序分量在α β坐标系下存在式（10）所示关系。

通过式（9）、（10）即可得到SDR 控制器的控制结构框图如附录B 图B3 所示。经上述分析可知，通过SDR 控制器后换相电压正、负序分量被解耦，负序分量对输出的正序分量影响将大幅减小。

2.2 SGOI-QSG结构

由于SOGI-QSG 具有一定的滤波功能，在产生90°相位偏移方面被广泛应用［18］，典型的SGOI-QSG结构图如附录B 图B4 所示。SGOI-QSG 的输出电压信号v′(s)及滞后其90°的输出电压信号v′q(s)对于输入电压信号v(s)的传递函数D1(s)、Q1(s)表达式如式（11）所示。

式中：k为传递函数D1(s)、Q1(s)的阻尼系数；ω′为角频率。不同k值下，D1(s)、Q1(s)伯德图见附录B 图B5。由图可知：SGOI-QSG 含有滤波特性；其滤波特性与k值负相关，其动态响应则相反。因此，为兼顾二者的平衡性，取k=［18］。

2.3 正交谐波消除法

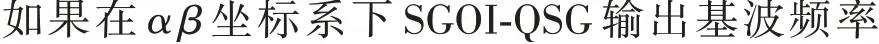
图1 QHCM结构图Fig.1 Structure diagram of QHCM

2.4 改进DSOGI-PLL结构

改进DSOGI-PLL 结构框图如附录B 图B7 所示。有较多文献已经对SRF-PLL 进行了详细介绍［19］，同时PNSC 模块为代数运算［18］，此处不再对以上2个环节进行介绍。

采集的电压信号首先进行Clark 变换；然后依次通过SDR 控制器、SOGI-QSG 实现正、负序电压分量的分离并消除部分谐波分量的影响；再经过QHCM滤除低次谐波电压分量；最后误差信号被输入比例积分控制器中，实现同步电压的锁相。通过前文分析可得改进后锁相环的整体伯德图见附录B图B8。

3 仿真验证

3.1 改进的DSOGI-PLL性能分析

在PSCAD／EMTDC 仿真平台中搭建电力系统，其由相电压为30 kV的电源以及有功功率为0.27 MW、无功功率为-0.1 Mvar 的负载构成。采用谐波注入的方法来验证不同锁相环的性能。在0.05 s 时，电压幅值跌落至0.8 p.u.，并添加表1 所示的各次谐波电压的正序、负序分量（均为标幺值）；同时假设测量过程中含0.05 p.u.的直流电压分量。附录C图C1为三相电压波形，由图可知，在0.05 s 后三相电压不平衡且有较大的谐波。

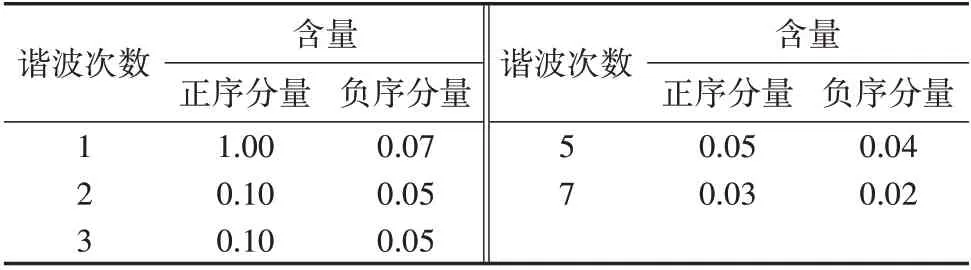
表1 各次谐波电压含量Table 1 Contents of each harmonic voltage

此时三相电压经Clark 变换得到的uα、uβ以及SDR 控制器输出的u+α、u+β与三相电压经快速傅里叶变换分解得到基波电压后经Clark 变换得的uα0、uβ0分量对比如附录C 图C2 所示。对比图中的曲线可知，uα、uβ的 波 形 畸 变 较 为 严 重，而u+α、u+β波 形 与uα0、uβ0较为接近，说明SDR 控制器能够较好地实现正、负序电压分离，从而使输出更加接近基波分量。

将改进的DSOGI-PLL 与SRF-PLL、DSOGI-PLL进行对比，对比结果如附录C 图C3 所示。设置锁相环的比例、积分参数分别为Kp=10、Ki=50［6］。根据相关标准，电力系统应在（50±0.2）Hz 的频率范围内波动，而中、小型容量的系统可在（50±0.5）Hz［20］的频率范围内波动。对比图C3中的结果可以发现，在三相电压平衡、不含谐波时，3 种锁相环输出的相位误差、频率波动相对较小；当a 相电压ua跌落至0.8 p.u.，并注入谐波时，不同锁相环作用下仿真波形出现较大差异。其中，SRF-PLL、DSOGI-PLL 在相位误差以及频率方面存在较大的误差，无法准确追踪电网电压。改进的DSOGI-PLL 由于采用了SDR 控制器减少了负序分量对锁相环的影响，同时正交谐波消除模块也有效地消除了谐波的影响，使改进的DSOGI-PLL 达到较高的锁相精度。图2 为改进的DSOGI-PLL 输出频率波形，由图可知其频率在0.018 s 后基本收敛在稳定的波动范围内。

图2 改进的DSOGI-PLL输出频率Fig.2 Output frequency of improved DSOGI-PLL

图3 为改进的DSOGI-PLL 输出相位追踪图，图中ua为标幺值。由图可知：改进的DSOGI-PLL 无论在电压平衡与否的情况下均可以锁定电压相位；满足精度的同时其在抗干扰力和动态响应速度方面也具有较大的优势。因此，改进的DSOGI-PLL 具有实用性。

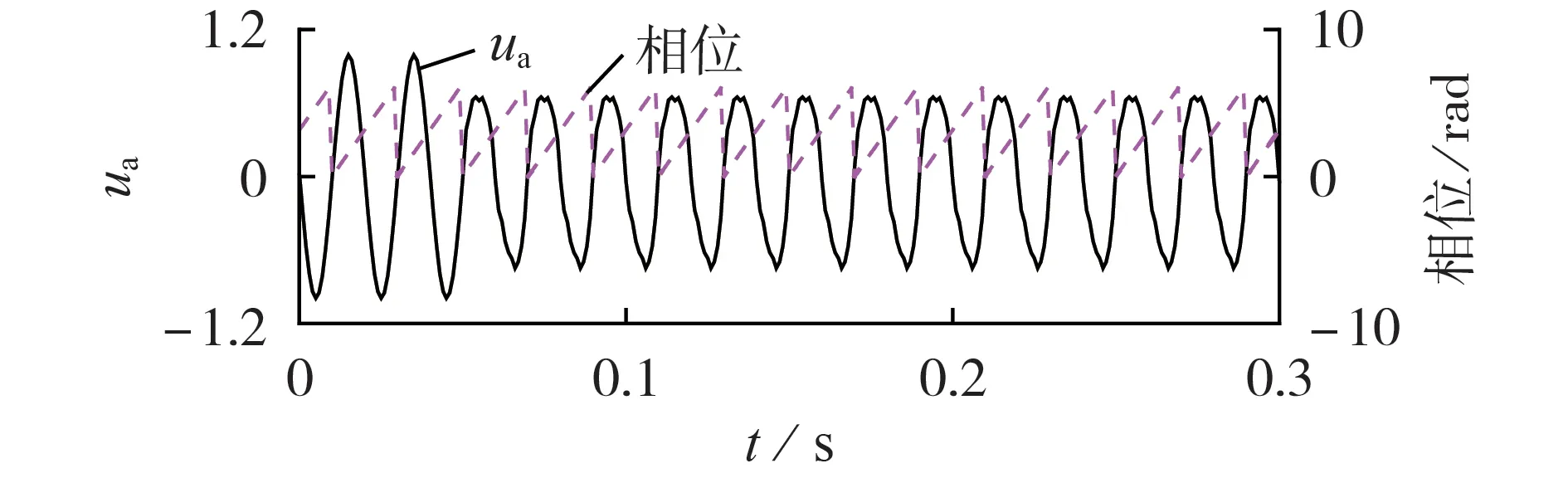
图3 改进的DSOGI-PLL输出相位Fig.3 Output phase angle of improved DSOGI-PLL

为了验证改进的DSOGI-PLL 针对不同情况的适应性，采用PSCAD／EMTDC 中自带的锁相环测试系统进行分析，同时与文献［6］中提及的级联延迟信号消除法锁相环（CDSC-PLL）进行对比，锁相环比例积分参数的设置情况与3.1 节相同。所搭建的测试系统由相电压为66 kV 的电源以及有功功率为0.27 MW、无功功率为-0.1 Mvar 的负载构成。在0.5 s 时电源电压相位发生90° 跳变，1.5 s 时发生单相接地短路故障，并在2 s 时切除负荷。此时2 种锁相环的相位误差、频率波动对比结果如附录C 图C4所示。对比图中结果可以发现：稳态时2种锁相环输出的相位误差、频率波动相对较小；当出现相位跳变、接地短路故障以及切除负荷时，2种锁相环的仿真波形出现较大的差异，其中CDSC-PLL达到稳定的速度较慢，其受到的干扰较严重，而改进的DSOGI-PLL可以有效避免这些情况引发的干扰。

3.2 不同锁相触发下LCC-HVDC输电系统运行特性

3.2.1 对比不同锁相环的基本特性

基于CIGRE HVDC 模型构建的LCC-HVDC 输电系统仿真模型见附录C 图C5。设2种锁相环方案对比分析交流系统发生不同故障后LCC-HVDC输电系统的运行特性：方案1，采用CIGRE HVDC 模型中锁相环进行仿真；方案2，将方案1 中锁相环改为改进的DSOGI-PLL，其参数与CIGRE HVDC 模型中的锁相环相同。

实际LCC-HVDC输电系统中发生较多的故障为感性故障，且容易诱发换相失败。因此，本文设置2种经电感Lf的接地故障，Lf大小代表故障的严重程度，具体工况设置如下。

1）工况1：设2 s 时逆变侧换流母线处发生单相接地故障，Lf=1.1H，持续时间为0.5 s。在此工况下，LCC-HVDC 输电系统在锁相环方案1、2 下逆变侧直流电压Udc、直流电流Idc、直流传输功率P以及熄弧角γ的变化情况如附录C 图C6 所示，图中Udc、Idc及P均为标幺值，后同。由图可知，对于类似较轻故障，采用锁相环方案1、2 时LCC-HVDC 输电系统均未发生换相失败，且基本不会引起任何不良后果。

2）工况2：设接地电感为Lf=0.35 H，其余参数设置情况与工况1 相同。在此工况下，LCC-HVDC 输电系统在锁相环方案1、2 下逆变侧直流电压、直流电流、直流传输功率以及熄弧角的变化情况如图4所示。由图可知，Lf=0.35 H 时系统的不平衡程度以及谐波均较为严重，采用锁相环方案1 并不能够准确地检测基波电压相位，影响了触发脉冲的准时性，导致LCC-HVDC 输电系统发生2 次换相失败。由于LCC-HVDC 输电系统控制效果有限，首次换相失败难以避免，但采用锁相环方案2 能有效避免发生多次换相失败。同时对比图4 所示直流传输功率曲线可以发现，与采用锁相环方案1 下的模型相比，采用锁相环方案2 后的LCC-HVDC 输电系统直流传输功率恢复能力更强。这说明改进的DSOGI-PLL 不仅可以有效避免LCC-HVDC输电系统发生多次换相失败，而且对系统在故障后的恢复作用也有一定帮助。

图4 工况2下2种锁相环方案的对比Fig.4 Comparison of two PLL schemes in Condition 2

另外，采用锁相环方案1、2 时逆变侧换流母线的换相电压负序分量1—4 次谐波电压对比情况如附录C 图C7 所示。由图可知：在故障期间，当采用锁相环方案1 时LCC-HVDC 输电系统的控制系统在调控的过程中也会产生换相电压负序分量，该换相电压负序分量甚至有可能大于系统故障时产生的换相电压负序分量；而采用锁相环方案2 时，系统仅在故障时存在较大的换相电压负序分量，而在后续故障持续期间换相电压负序分量各次谐波电压含量明显降低，说明改进的DSOGI-PLL 有利于LCC-HVDC输电系统控制调节作用，抑制了换相电压负序分量的产生，从而有助于系统的后续换相，减少了多次换相失败发生的概率。

采用锁相环方案1、2 时整流、逆变侧触发角的对比情况如图5 所示。通过图中的对比曲线可以发现采用锁相环方案1 时，在故障情况下整流、逆变侧的触发角将发生多次的剧烈变换，进而导致系统发生多次换相失败；而采用锁相环方案2 时，整流、逆变侧的触发角仅在故障时有一次剧烈变化而后快速收敛至稳定值，从而避免发生多次换相失败。这再次说明了改进的DSOGI-PLL 能够降低多次换相失败发生的概率。

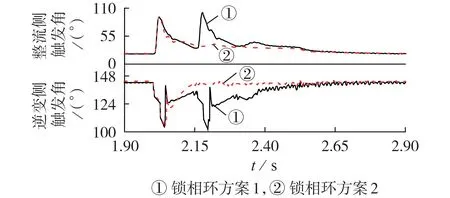
图5 2种锁相环方案下的触发角对比Fig.5 Comparison of trigger angles between two PLL schemes

最后，为了验证改进的DSOGI-PLL在LCC-HVDC输电系统中应对其他故障类型的控制效果。在工况2 的基础上改变系统的故障类型，同时加入文献［6］提及的CDSC-PLL 进行对比分析。在三相短路、相间接地短路、相间短路故障下LCC-HVDC 输电系统熄弧角的变化如附录C 图C8 所示。对比图5 及图C8 可以发现，改进的DSOGI-PLL 在不同故障类型下均具有波动抑制效果，对系统换相具有一定的改善作用，而CDSC-PLL 在相间接地短路故障及相间短路故障类型下的改善效果较弱。

3.2.2 对比不同故障水平下锁相环的控制特性

定义故障水平fFL表示系统故障的严重程度［1］，其表达式如式（16）所示。

式中：UN、ω分别为额定电压、额定角频率；PN为额定功率。

设故障发生时刻为第2 s，持续时间为0.5 s。在单相接地短路、三相短路、相间接地短路以及相间短路故障下根据式（16）进行故障水平计算，不同故障水平下采用锁相环方案1、2 时换相失败次数如附录C 表C1 所示。由表可知：在不同故障类型下，故障持续期间采用锁相环方案1 后LCC-HVDC 输电系统发生多次换相失败；而采用锁相环方案2 后仅发生首次换相失败。这说明改进的DSOGI-PLL 在故障期间可以对换相电压正、负序分量有效解耦，并消除换相电压负序分量及谐波的影响，快速地追踪电网电压的频率与相位，为LCC-HVDC 输电系统提供准确、可靠的触发信号。

3.2.3 对比不同短路比下锁相环的控制特性

调整逆变侧交流系统的阻抗以提高系统短路比，进一步验证改进的DSOGI-PLL 在LCC-HVDC 输电系统中的控制效果。设附录C 图C5 方框中系统等效串联阻抗为R=2.738 3 Ω、L=0.032 5 H，此时系统的短路比为5。不同故障水平下锁相环方案1、2下LCC-HVDC 输电系统的换相失败次数如附录C 表C2所示。

对比表C1及表C2可以发现，系统短路比增大后LCC-HVDC 输电系统发生多次换相失败的次数有所减少，但当短路比为5 时LCC-HVDC 输电系统在采用锁相环方案1 时仍然会出现多次换相失败，而采用锁相环方案2 时未出现该情况，再次验证了改进的DSOGI-PLL能够降低多次换相失败发生的概率。

4 结论

针对LCC-HVDC输电系统在逆变侧故障时容易发生换相失败的问题，本文基于逆变侧交流系统故障下换相电压负序分量的分析结果，提出了一种改进的DSOGI-PLL，并验证了其控制效果，所得结论如下：

1）改进的DSOGI-PLL 的动态响应效果好，其在负序、谐波抑制方面具有较大的优势；

2）当电网电压不平衡及谐波含量较高时，改进的DSOGI-PLL 仍能够高效地追踪电网电压的频率与相位；

3）由于改进的DSOGI-PLL在负序分量以及谐波抑制方面具有较好的鲁棒性，将其应用于LCC-HVDC输电系统中可以有效降低多次换相失败的发生概率，进而为实际工程中多次换相失败的抑制提供参考。

本文研究了换相电压负序分量对LCC-HVDC输电系统底层锁相触发控制环节的影响，换相电压负序分量还会对LCC-HVDC输电系统其他控制环节造成不利影响，后续将进行深入研究。

附录见本刊网络版（http：//www.epae.cn）。