旋转控制头密封胶芯性能三维有限元分析与结构优化*

郭良林 宋顺平 李 刚 李俊雄 韩雪莹 夏成宇

(1.长江大学机械工程学院 湖北荆州 434023；2.川庆钻探工程有限公司长庆钻井总公司 陕西西安 710018)

当井底压力低于地层孔隙压力，地层液体可以进入井筒并循环至地面进行有效处理的钻井方法，称为欠平衡钻井[1]，因其可降低地层损害、提升钻井效率而被广泛运用于工程实际。石油钻采过程中，井喷事故会造成人员伤亡与较大的经济损失，并扰乱正常的工作秩序[2]。旋转防喷器(RBOP)是欠平衡带压起下钻过程中重要的井控装备[3]，可有效预防井喷事故的发生。RBOP胶芯用以密封钻杆与井筒之间的环空，它与钻杆间的接触压力极大地影响着防喷器的密封性能[4]。现如今，欠平衡钻采作业中对胶芯密封性能要求越来越高，而国内生产的旋转控制头胶芯密封性与国外同类产品存在较大差距[5-7]。因此，改善胶芯的密封性能可有效提高作业安全性，降低经济损失，推进带压设备的国产化进程。

欠平衡钻井过程中，由于需要反复进行起钻与下钻操作、反复过钻杆本体与钻杆接头，胶芯密封面受交变循环应力而易产生疲劳失效[8]，如图1所示。因此，在满足密封要求的前提下，需要降低接触面上的应力幅值。目前常用2种方法描述橡胶材料的力学性能：第一种基于热力学统计方法，认为橡胶中熵的减少致使橡胶弹性力恢复；另一种是唯象学理论，将橡胶视作连续介质，用应变能密度来描述橡胶的力学性质[9]。许多学者基于现象学理论建立了胶芯动态密封CAE模型，并对其密封性能进行了研究。2002年，王复东[10]利用ANSYS软件对旋转控制头胶芯进行有限元分析，研究了井压、过盈量、摩擦等对胶芯与钻杆间的接触压力的影响，并运用现场实验证明了仿真方法的有效性。2007年，付海龙等[11]在COMSOL软件上建立过油管防喷器分析模型，并通过改变油室控制压力及胶芯长径比改进了胶芯的密封性能。2008年，LI和ZHANG[12]通过ABAQUS软件建立了胶芯有限元模型，分析了欠平衡带压起下钻过程中胶芯与钻杆之间的接触压力分布规律。2012年，魏晓东等[13]基于Mooney-Rivlin本构模型，对井口偏心工况下的接触情况进行了分析。2015年，刘亮等人[14]探讨了胶芯在不同密封环境下的失效机制。2017年，HU等[15]基于橡胶的超弹性本构和有限元分析方法，探讨炭的粒径与含量对胶芯密封性能的影响；马卫国等[16]选用Ogden模型作为胶芯本构模型，研究了井筒压力对带压作业防喷器闸板胶芯的疲劳寿命及密封失效的影响。2019年，姚尧等人[17]基于载荷迭代方法，对煤层气井气控环形防喷器胶芯各变形阶段的接触压力方程进行推导，并通过有限元仿真进行验证。2020年，何宇航等[18]基于单轴拉伸与压缩试验确立橡胶材料本构关系，并探讨常用钻杆与胶芯的最优搭配组合。

综上所述，胶芯结构、橡胶材料种类与配方、实际工况等是影响钻杆与胶芯间接触压力和胶芯使用寿命的重要因素。而目前的研究大多基于有限元仿真方法来分析单一因素对胶芯密封性能的影响、胶芯材料配方优选与接触压力分布规律。本文作者考虑到因素间的耦合作用，基于橡胶单轴压缩试验结果，选用Yeoh模型作为胶芯变形过程中的本构模型，运用ABAQUS试验平台建立胶芯三维有限元模型，分析起下钻过程中胶芯动态密封过程与密封面受力情况；分析单个胶芯结构参数变化对接触压力的影响，并基于正交试验在胶芯内、外锥角与内径等参数共同作用下时对胶芯结构进行优化，通过现场应用验证仿真分析的准确性。

1 动态密封力学方程

带压起下钻时，胶芯在起密封作用的同时会因产生大变形而进入塑性状态，胶芯与钻杆间的接触和密封过程是一个复杂的非线性问题[19]。利用虚功原理可以建立动态密封过程的有限元控制方程：

∭vσijδεi jdv=∭vxiδuidv+∬sxiδuids

(1)

式中：σij为静力允许应力；δεi j为虚应变；v为给定的体积力边界；xi为单位载荷矢量；δui为虚位移；s为给定的面力边界。

2 胶芯动态密封有限元分析

2.1 橡胶芯材料参数的确定

2.1.1 单轴压缩试验

为确定丁腈橡胶材料的本构关系，首先对橡胶试样进行单轴压缩试验。试验设备选用图2(a)所示的万能材料试验机，并选用图2(b)所示的圆柱状试样，试样直径为(29.0±0.5)mm，高度为(12.5±0.5)mm，基于标准GB/T 2941—2006和GB/T 7757—1993进行试验[20-21]，取5组数据的平均值作为试验结果。

2.1.2 Yeoh本构模型

基于唯象学理论的常见本构模型有Mooney-Rivlin、Yeoh与Ogden 3种，运用ABAQUS软件将单轴压缩试验数据分别与上述3种本构模型进行拟合，结果如图3所示。Yeoh本构关系的拟合程度较高，因此文中选用Yeoh本构模型来描述带压起下钻过程中胶芯的应力-应变关系，拟合所得模型系数为C10=1.117 MPa，C20=0.059 MPa，C30=0.412 MPa。

2.2 CAE模型的建立

以国产11.67 mm钻杆的下部自封式胶芯为研究对象，其中胶芯由胶芯本体与铁芯组成，钻杆由钻杆接头与钻杆本体组成。根据钻杆与胶芯结构，建立胶芯动态密封三维有限元模型，如图4所示。其中钻杆均设为解析刚体，胶芯与铁芯均设为可变形体，胶芯本体与铁芯之间的接触类型为绑定，钻杆与胶芯本体之间的摩擦因数设为0.3，并将7 MPa的井口压力均布于胶芯外表面，铁芯上表面为全约束。以六面体C3D8R划分三维模型网格，网格数为52 204。设定初始方案中内锥角为28°，外锥角为60°，胶芯内径为72 mm，以0.75 m/s的速度带压起下钻。

2.3 密封面受力情况

为分析胶芯在密封过程中的受力情况，在密封面上自上而下取19个点，如图5所示，并按1～19对其进行编号，对接触压力创建场变量输出。该19个点在起钻过程中平稳过接头时刻的接触压力如图6所示，从点1至点11接触压力整体呈上升趋势，点11至点19接触压力整体呈下降趋势，点11为主密封面与内锥面间的拐点。由此可知，在胶芯内锥面与主密封面相交处容易产生应力集中现象。

图7与图8分别显示了利用三维有限元分析时平稳过接头时刻的接触压力与Mises应力云图，主密封面较之其他部位的接触压力与Mises应力更大。

在胶芯主密封段自上而下取3个点，观测起下钻过程中接触压力变化情况，变化规律如图9所示。初始时刻(t=0)，钻杆与胶芯尚未接触；0～t1为下钻过程中钻杆本体逐渐插入胶芯时段，t1～t2为下钻过程中钻杆本体第一次平稳过胶芯时段，t2～t3为下钻过程中钻杆接头逐渐插入胶芯时段，t3～t4为下钻过程中钻杆接头平稳过胶芯时段，t4～t5为下钻过程中钻杆接头逐渐捅出胶芯时段，t5～t6为下钻过程中钻杆本体第二次平稳过胶芯时段；t6～t7为起钻过程中钻杆本体第一次平稳过胶芯时段，t7～t8为起钻过程中钻杆接头逐渐插入胶芯时段，t8～t9为起钻过程中钻杆接头平稳过胶芯时段，t9～t10为起钻过程中钻杆接头逐渐捅出胶芯时段，t10～t11为起钻过程中钻杆本体第二次平稳过胶芯时段。起下钻过程中，钻杆本体平稳过胶芯时的接触压力低于钻杆接头平稳过胶芯时的接触压力，钻杆本体第一次与第二次平稳过胶芯时的接触压力相等；钻杆本体和钻杆接头在下钻过程中平稳过胶芯时的接触压力比起钻过程中平稳过胶芯时略低；钻杆本体和钻杆接头过胶芯时的过渡段，接触压力变化幅度较大。

3 胶芯结构参数的影响及优化

3.1 单因素对密封性能的影响

带压起下钻过程中，旋转控制头胶芯的结构极大地影响着其密封性能。为更好地改进胶芯结构，通过一次因子试验分别对不同内、外锥角与内径情况下胶芯与钻杆间的接触压力进行分析，得出单个胶芯结构参数变化对接触压力的影响规律。

3.1.1 内锥角对接触压力的影响

钻杆与胶芯间的密封面可分为主密封面与辅助密封面，内锥面为辅助密封面，在起下钻过程中起过渡与辅助密封作用[22]。如图10所示，胶芯内锥角为主密封面与辅助密封面间的夹角；固定点A，当点B朝B1移动时，内锥角增大，朝B2移动时减小。分别在内锥角为25°、30°、35°、40°的情况下分析主密封段胶芯与钻杆间接触压力作用规律，提取起钻过程中平稳过钻杆接头时刻密封面上的接触压力，结果如图11所示。图11中，波峰处为主密封面与辅助密封面间的拐角，波峰之前为辅助密封面，波峰之后为主密封面；随着内锥角的增大，辅助密封面上接触压力逐渐增加，主密封面上变化不大。当内锥角增大时，内锥面附近胶芯体积有所增加，密封过程中钻杆与胶芯在该处的过盈量有所增加，从而使得内锥面上接触压力变大。

3.1.2 外锥角对接触压力的影响

如图12所示，外锥角为胶芯外锥面与底面的夹角；固定点A，当点C朝C1移动时，外锥角减小，朝C2移动时增大。分别在外锥角为57°、60°、63°、66°、69°的情况下分析主密封段胶芯与钻杆间接触压力作用规律，并提取整个起下钻过程中密封面上的接触压力峰值与Mises应力最大值，结果如图13所示。可知，外锥角增大时，密封面上接触压力峰值与Mises应力最大值均有所波动，其中外锥角为69°时最小。当外锥角变化时，胶芯厚度产生变化，对抗压性产生影响，又由于井口压力方向与外锥面垂直，外锥角变化时会引起外压的作用方向产生变化。由此，外锥角的变化会影响密封面受力情况，其应力峰值也会产生变化。

3.1.3 内径对接触压力的影响

胶芯内径d是影响接触程度的重要因素，其变化过程如图14所示，由d变为d1时，内径增大。分别在内径为65、70、75、80、85 mm的情况下分析主密封段胶芯与钻杆间接触压力作用规律，并提取起钻过程中过钻杆接头时刻密封面上的接触压力，结果如图15所示。图15中，波峰之前为辅助密封面，波峰之后为主密封面；随着胶芯内径的增大，主密封段接触压力有所降低。增大胶芯内径将减小主密封段胶芯与钻杆间的过盈量，从而减小钻杆通过时胶芯的张紧力，接触显著降低。

3.2 基于正交试验的结构参数优化

在胶芯大变形过程中，各结构因素并非独立影响，还存在耦合作用，所以进行优化前需要充分考虑多因素共同作用带来的影响。文中采用正交试验设计从多个试验因素组合中进行优选[23]。

将有限元分析与正交试验相结合，基于数值模拟试验结果得出各试验方案中σc(接触压力)的范围与σm(Mises应力)的幅值σa，记钻杆本体平稳过胶芯时的最小Mises应力为σm(min)，记钻杆接头平稳过胶芯时的最大Mises应力为σm(max)，则：

(2)

由于最低密封要求为7 MPa，所用丁腈橡胶芯材料许用应力值为25 MPa，记起下钻过程中密封面间最小接触压力为σc(min)、最大接触压力为σc(max)，则建立如下优选模型：

(3)

st.σc(min)>7

σc(max)<25

选定内锥角A、外锥角B、胶芯内径C作为试验因子，设定起下钻速度v=0.75 m/s，以提升胶芯密封性能和使用寿命为试验目标，选用L9(34)正交表，进行三水平三因素试验，试验因子及其水平安排见表1，9次试验方案及其结果见表2。

表1 试验因子及其水平

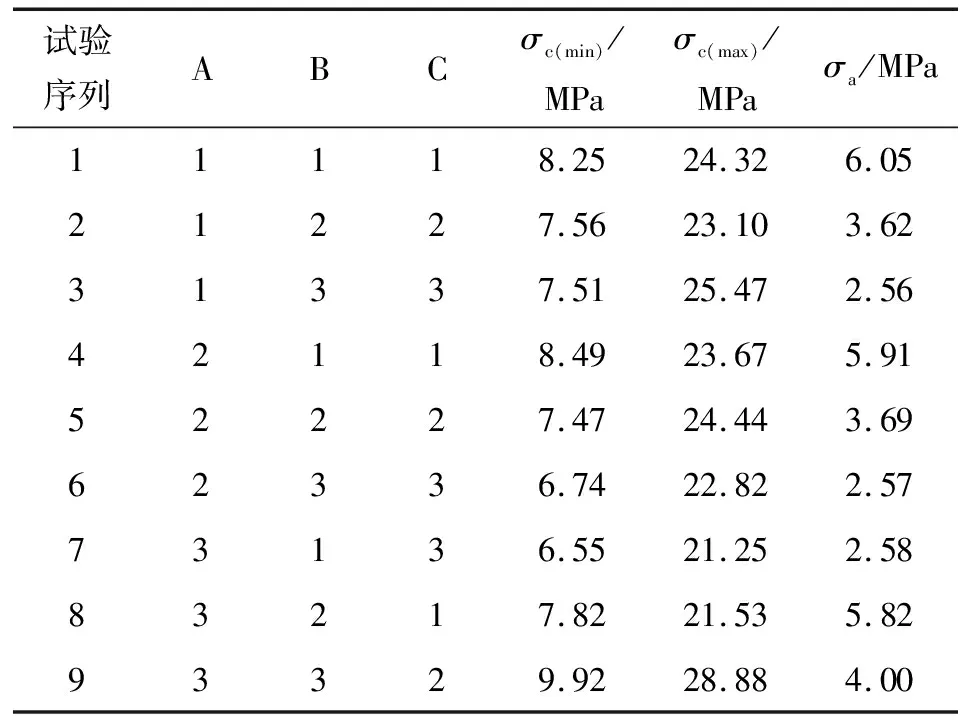
表2 正交试验结果

由表2可知，不满足优选模型条件的为第3次、第6次和第7次试验，其余6组试验中，第2次试验的Mises应力幅值σa最小。极差分析指将每一列的极差求解出来，因子的影响越大，极差越大[24]。对9组试验的Mises应力幅值进行极差分析，Wi表示某试验因子在第i水平下的Mises应力幅值总和，wi表示试验因子在第i水平下分析的Mises应力幅值算术平均值，θ为极差，极差分析结果见表3。可知，试验中各试验因子对Mises应力幅值的影响按从大到小排序为胶芯内径、外锥角、内锥角，根据极差分析结果所取的最优解为A2B3C3，其试验因子与第6次试验的相同，不满足密封要求。

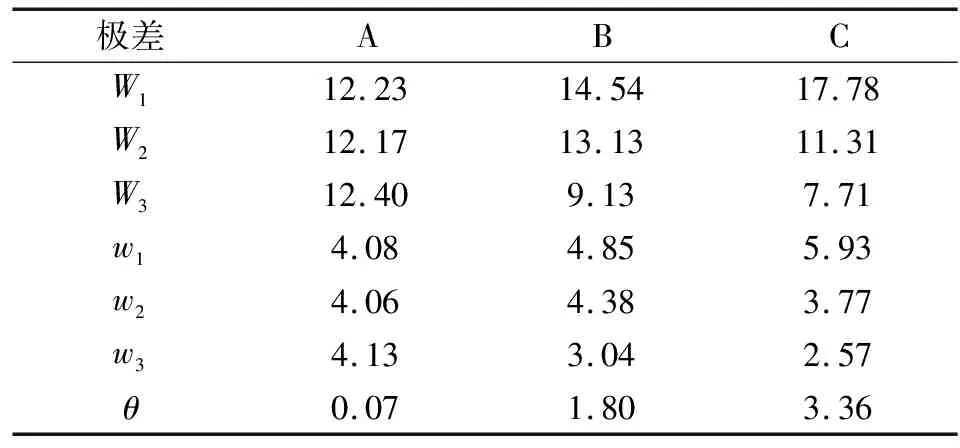
表3 极差分析及其结果

综合考虑，以正交试验第2次试验方案为最优方案，该方案中各试验因子水平数为A1B2C2。如表4所示，将初始方案与优化后试验方案的仿真分析结果进行对比，2种方案均能满足密封要求，且接触压力峰值低于材料许用应力值;但优化方案的接触压力峰值降低了0.51 MPa，Mises应力幅值降低了57.5%，受交变循环应力而发生疲劳失效的周期将会有所增长。

表4 优化前后结果对比

4 胶芯现场应用

结构优化前胶芯在钻采过程中的平均使用寿命为90 h，密封性可满足一般钻采要求。将优化后的胶芯运用于四川盆地多个油田钻采现场，现场应用结果如表5所示。可知，优化后胶芯的密封性能良好，能够满足欠平衡带压起下钻过程中的钻采要求，且寿命有所增长，从而证明了胶芯三维有限元仿真结果的正确性。

表5 现场应用相关参数

5 结论

(1)胶芯主密封面的接触压力大于其他部位，主密封面与内锥面拐点处取最大值，该处易产生应力集中效应。欠平衡起下钻过程中，起钻时的接触压力更大，过钻杆本体时的接触压力低于过钻杆接头。

(2)分析单一结构参数对接触压力的影响，结果表明：内锥角增大时，辅助密封段接触压力增大；外锥角变化时，起下钻过程中密封面接触压力峰值与Mises应力最大值产生波动；内径增大时，主密封段接触压力减小。考虑多因素耦合作用，基于正交试验优化的结构参数组合为内锥角24°、外锥角64°、内径79 mm，对应的试验因子水平为A1B2C2。相比初始方案，优化方案的接触压力峰值降低了0.51 MPa，Mises应力幅值降低了57.5%，受交变循环应力而发生疲劳失效的周期将会有所增长。极差分析结果显示：对主密封面Mises应力幅值的影响程度排序依次为胶芯内径、外锥角、内锥角。

(3)对优化后的胶芯在珙县、东安等地区的油田进行现场应用，得出胶芯在优化后密封性能可满足钻采要求，且胶芯密封面寿命较之优化前有所增长，验证了胶芯三维有限元仿真分析的正确性。