旋转轮胎中压电悬臂梁离心距优化

张云顺，赵香帅，王万树

(1. 江苏大学 汽车工程研究院，江苏 镇江 212013；2. 筑波大学 系统信息工程学院，日本 筑波 3058573)

0 引言

随着微电子处理技术的发展，无线传感器已广泛应用于各种设备中，但如何为无线微传感器提供永久电源是目前面临的主要问题[1]。近年来，压电式振动能量采集器大多采用悬臂梁结构，其理论分析模式是基于线性结构存在频率响应单一性问题。Leadenham等[2]利用非线性系统将激励与谐振子间的耦合扩展到宽频带区域，以拓宽振动能量采集器的有效频率范围，但在低频区域提高采集器性能较难。

随机共振是指在弱周期信号中加入噪声，在一定概率内显著放大输出响应的现象。这一现象已被用于信号检测和故障诊断[3-4]、图像处理[5]和生物神经分析[6]等。已有研究成果表明，双稳态系统中随机共振现象可提高能量采集器回收的电能[7-9]。冷永刚等[10]建立了Duffing振子随机共振的判别函数，阐述了Duffing振子在不同噪声强度及信号频率输入条件下的广义调参随机共振规律。Zhang等[11]利用路面环境振动产生的噪声激励，成功地提高了悬臂梁的振动响应。Kim等[12]证明了旋转系统中随机共振频率的可调节特性。然而，上述基于随机共振的振动能量俘获研究，只讨论了在某一确定频率下的随机共振现象，尽管研究了可调节的随机共振，但并未对其进行进一步的参数优化。

本文提出了一种基于自调节随机共振的压电式振动能量采集器模型(简称压电悬臂梁)离心距优化方法。通过构建压电悬臂梁动力学方程，结合自调节随机共振优化离心距，与不可调节随机共振和不同离心距下的压电悬臂梁响应进行对比，结果表明基于自调节随机共振优化后的离心距能更好地拓宽能量采集频带，提高能量俘获性能，验证了本文提出的离心距优化方法。

1 随机共振的基本原理

双稳态系统的动力学方程[13]为

(1)

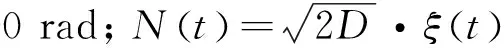
在无周期激励时，系统势函数在x=±(a/b)1/2处有2个对称的最小值，势阱高度ΔU=a2/(4)。在有周期激励下，双势阱呈不对称的上下倾斜，如图1所示。

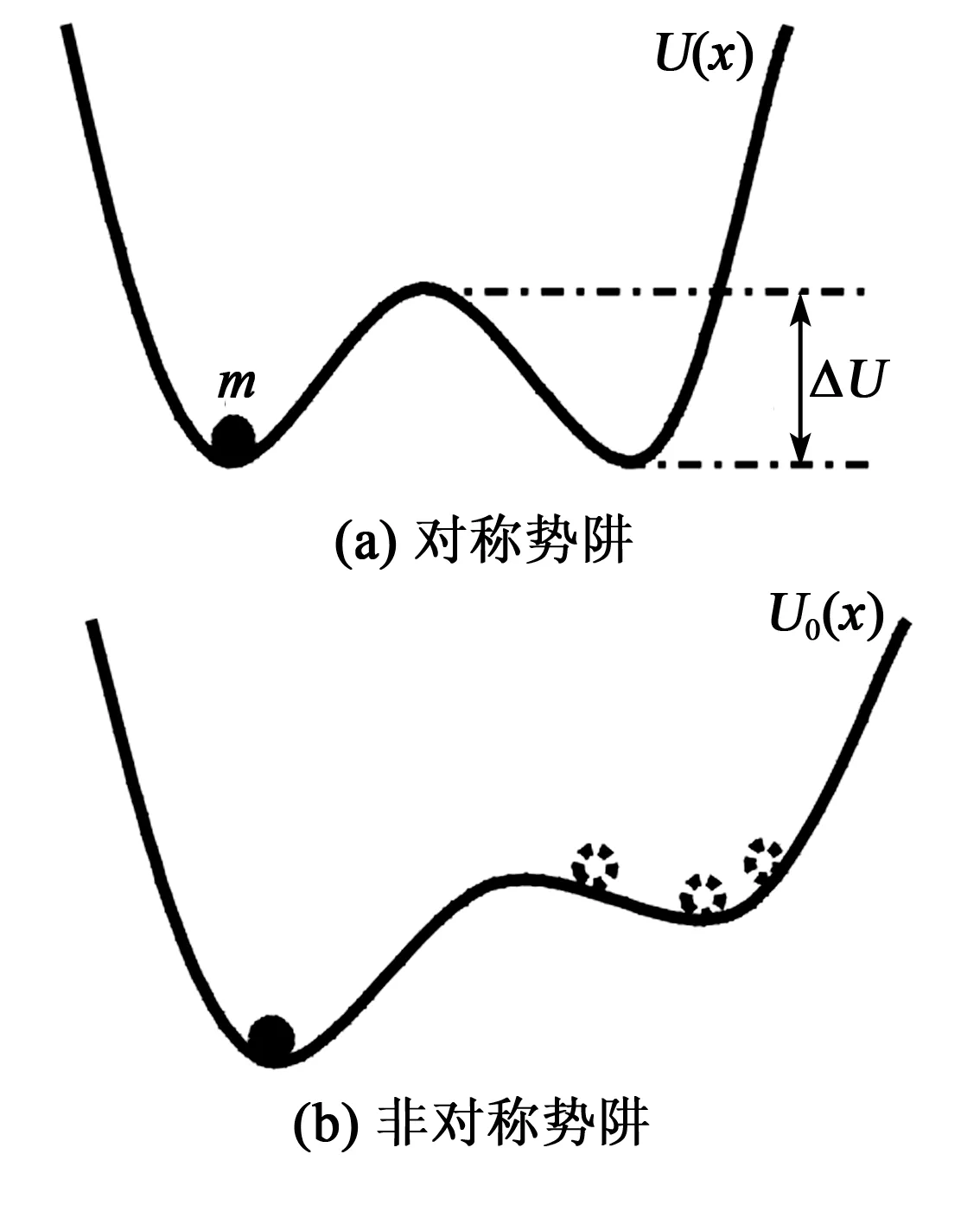
图1 势阱图

标准势能方程为

(2)

式(2)可转化为

(3)

当周期激励太弱不能使振子从某一势阱跃迁至另一势阱时，振子在某一势阱内振荡，而加入噪声激励后，振子获得足够的能量产生跳变，振子可在势阱间振荡。当振子阱间跃迁的平均等待时间Tw为周期激励周期Ts的1/2时，振子跃迁与势阱倾斜发生同步，即随机共振的发生条件为

Ts=2Tw

(4)

用Kramers逃逸速率γk定义Tw=1/γk，其中γk[14]为

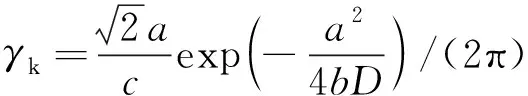
(5)

因此，由式(4)可知随机共振频率γ为

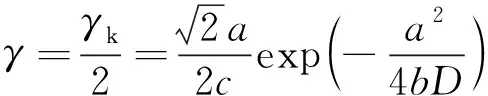
(6)

2 压电悬臂梁的理论模型

本文将压电悬臂梁安装在轮胎上，噪声激励来自于不可预知的路面粗糙度，加上车轮引起的周期性旋转力和磁体间的磁力，共同为随机共振的发生提供了必要条件。

图2为压电悬臂梁模型示意图。悬臂梁沿轮胎径向安装，包含2个磁铁，一个位于悬臂梁的自由端，另一个固定安装，其质量为m。压电悬臂梁绕y轴旋转，如果磁铁间距d调至合适值，在磁铁间的磁力FM的切向分量FH和悬臂梁恢复力kxT的共同作用下，悬臂梁末端磁铁会在两势阱间来回振荡，表现为双稳态特征。

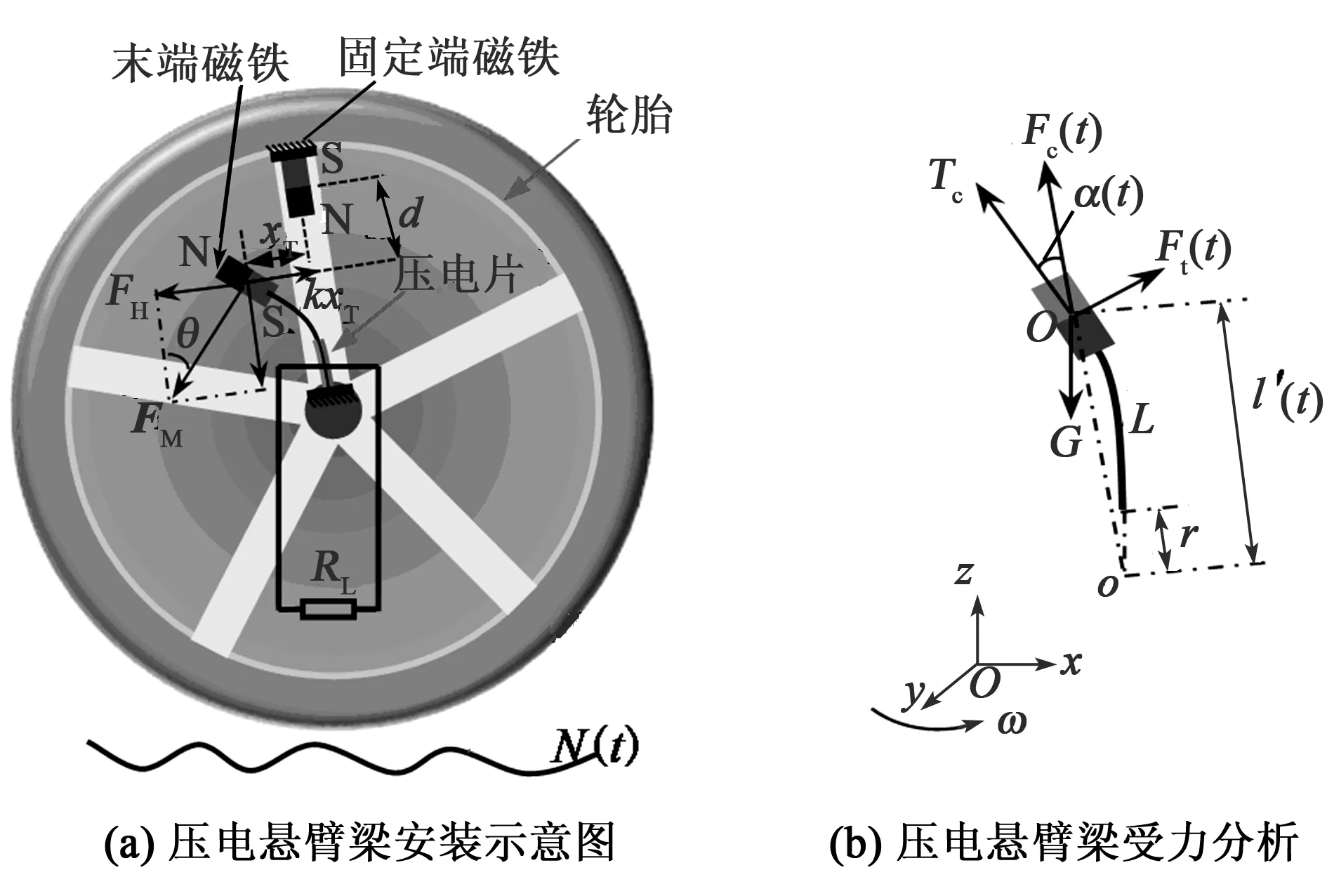
图2 压电悬臂梁模型示意图

磁铁间磁力切向分量FH可基于磁偶极子间的力学模型[15]：

FH=FMsinθ

(7)

式(7)在xT=0处进行泰勒展开并简化为

(8)

式中:Mf=(Mfx,Mfy),Mc=(Mcx,Mcy)分别为悬臂梁末端磁铁和固定端磁铁磁化强度的水平分量和垂直分量；v为磁铁体积；μ为真空中的磁导率；xT为末端磁铁切向的位移。

由磁力产生的线性项和非线性项系数分别为

(9)

(10)

磁力切向分量FH可进一步表示为

(11)

当压电悬臂梁以ω旋转时，悬臂梁末端磁铁离心力Fc(t)为

Fc(t)=mω2l′(t)

(12)

离心力切向分量为

Ft(t)=mω2l′(t)sinα(t)≈mω2l′(t)α(t)

(13)

式中：l′为末端磁铁重心到旋转中心的距离;α(t)为离心力Fc(t)与向心力Tc之间的夹角。

l′可表示为

(14)

式中：L为悬臂梁长度;r为悬臂梁根部到旋转中心的距离。

悬臂梁的静态偏转为

(15)

式中：E为杨氏模量;I为惯性矩;xp为悬臂梁尖端位置到载荷力P′的距离。

悬臂梁尖端的偏转角α(t)为

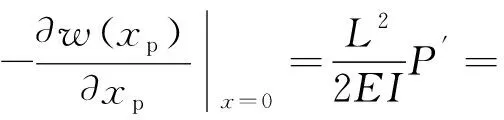
(16)

将式(14)、(16)代入式(13)可得离心力切向分量为

(17)

考虑离心力后的压电悬臂梁的机械方程为

θpV+[G+N(t)]sinωt

(18)

式中：H=L+r为末端磁铁的离心距(简称离心距)；k为悬臂梁刚度系数；V为负载端电压；θp为机电耦合系数；Cp为压电片的等效电容。

根据基尔霍夫定律，可得压电悬臂梁的电学方程为

(19)

式中RL为负载阻抗。式(18)、(19)描述了压电悬臂梁的振动能量俘获机理。因此，压电悬臂梁的等效刚度系数为

(20)

离心距H=0，即悬臂梁末端磁铁位于轮胎旋转中心时，磁铁不受离心力作用，等效刚度为常数。当H≠0时，等效刚度随旋转频率增加而增加，且不同离心距呈现不同的变化率，如图3所示。

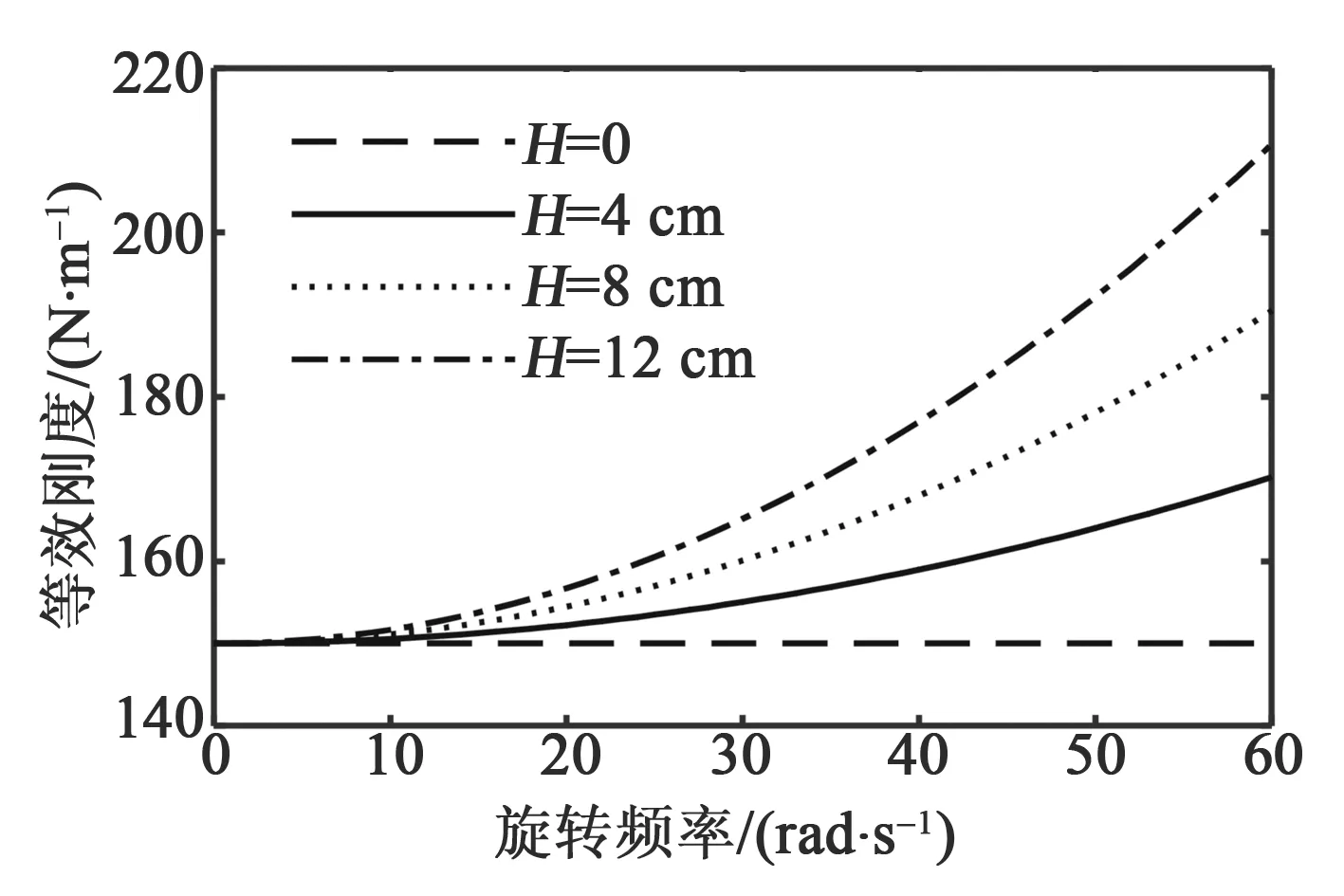
图3 等效刚度系数

3 压电悬臂梁在自调节随机共振下的离心距优化

随机共振的产生条件通常由Kramers逃逸速率定义。根据第2节的理论分析可知，伴随旋转频率的变动，系统的线性项系数呈现可调节性变化趋势。因此，随机共振频率同样呈现可调节性变化趋势即自调节随机共振。旋转环境下随机共振频率γ′可被进一步表示为

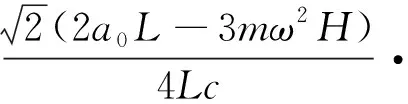
(21)

式中：a0=a′-k；c为阻尼系数。

为研究低频区域的自调节随机共振，通过分析式(21)可知存在最优离心距，在此离心距下，γ′(ω)与旋转频率能满足较高的匹配。当满足旋转频率等于γ′(ω)且与γ′(ω)相切时有

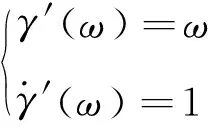
(22)

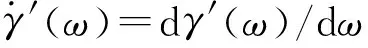
由式(22)可求出压电悬臂梁最优离心距。根据γ′(ω)进一步可将式(22)表示为

(23)

令λ=ω2H，联立式(22)中两个条件式，可得关于λ的方程：

bD)λ-2a0bLD=0

(24)

由式(24)可得：

(25)

其中：

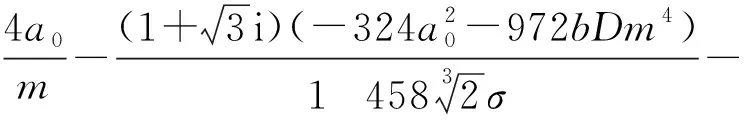
(26)

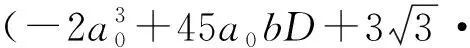
(27)

压电悬臂梁的最优离心距与其对应的频率点为

(28)

(29)

运用上述提出的压电悬臂梁最优离心距优化方法，计算可得最优离心距。

选取双稳态系统参数a0=75 N/m，b= 5.2×106N/m3，c= 0.25 N/(m·s-1)，D= 1.22×10-4N，不同离心距下随机共振频率曲线与旋转频率曲线的匹配结果，如图4所示，当离心距为最优解 8ψL/(6a0-mψ)2/c2exp[-(6a0-mψ)2/(72bD)]时，求得离心距为6.45 cm，随机共振频率曲线与旋转频率曲线在30～60 rad/s内相切,且重合良好。

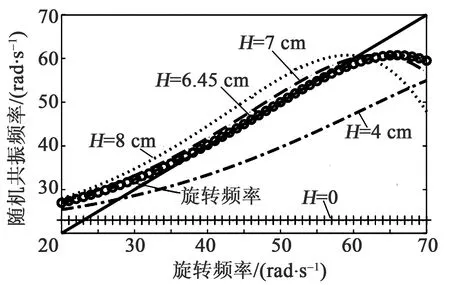
图4 随机共振频率与旋转频率匹配图

4 自调节随机共振对压电悬臂梁动态特性的影响

4.1 自调节与不可自调节随机共振频率的悬臂梁响应比较

本文在轮胎旋转处于低频区域(0～50 rad/s)环境下进行研究，当悬臂梁末端磁铁重心位于旋转中心即H=0时，磁铁不受离心力作用，随机共振频率不可调节。H≠0时，末端磁铁受离心力作用，悬臂梁等效刚度发生变化，随机共振频率可调节。压电悬臂梁的速度和位移相轨迹如图5所示。在低频区域，不可自调节随机共振的悬臂梁响应较差,如图5(a)所示。自调节随机共振的悬臂梁响应显著提高，如图5(b)所示。

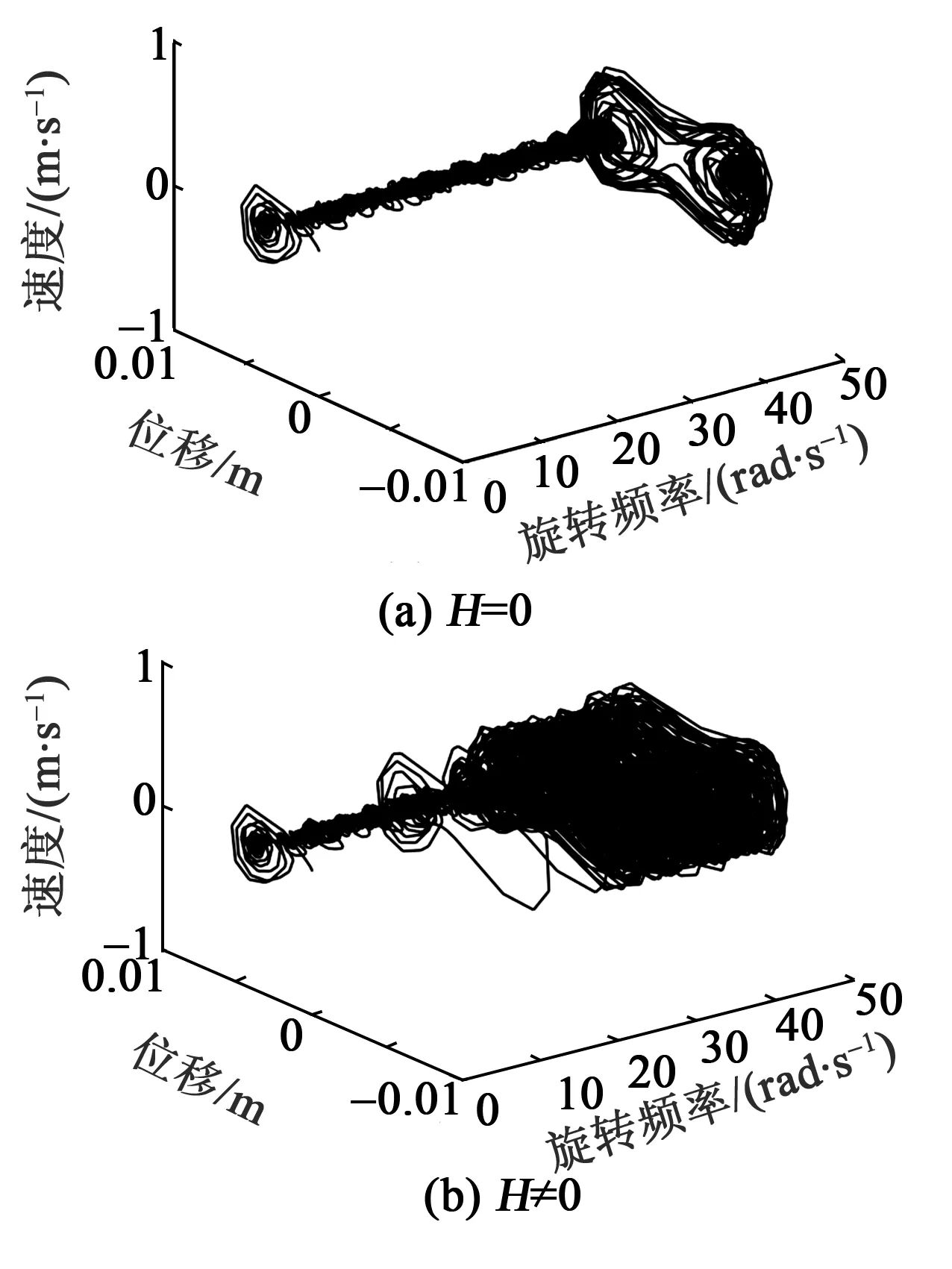
图5 压电悬臂梁的速度和位移相轨迹图

4.2 离心距对压电悬臂梁动态特性的影响

4.2.1 速度位移响应

本文所有数值模拟均在Matlab软件中采用龙格-库塔算法进行。压电悬臂梁参数如表1所示。

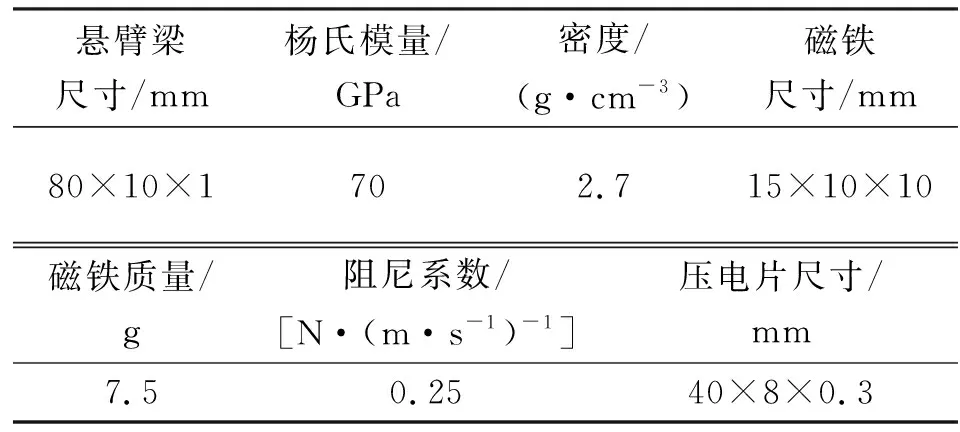
表1 压电悬臂梁参数

考虑到离心距对压电悬臂梁性能的影响，首先根据第3节的离心距优化法求出最优离心距H=6.45 cm，因此,离心距分别取0、4 cm、6.45 cm、7 cm、8 cm，分析压电悬臂梁在低频区域内的位移、分岔响应(图中，灰色线为位移响应，黑色点划线为分岔响应)和速度响应，如图6、7所示。

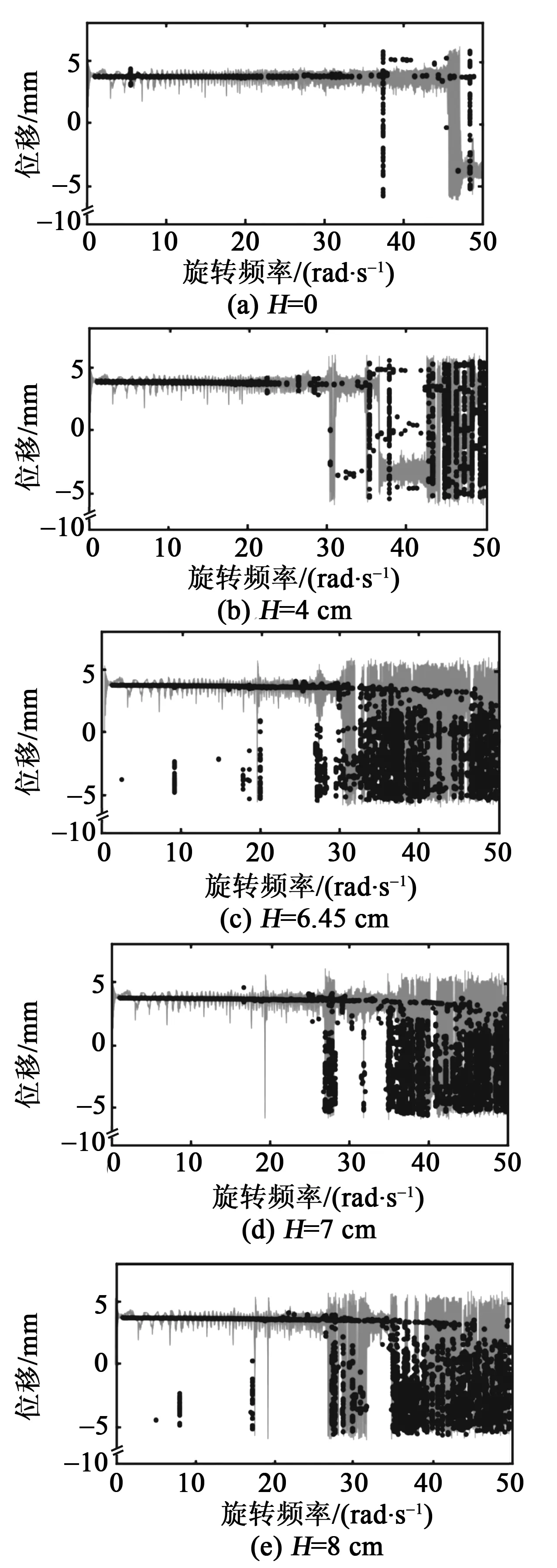
图6 不同离心距下的位移和分岔响应

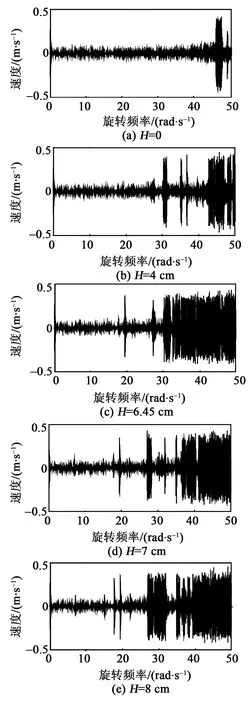
图7 不同离心距下的速度响应

在0～50 rad/s，当H=0时，悬臂梁末端磁铁在0～45 rad/s无足够的动能跃过势垒，做小幅低速运动，只在45～50 rad/s内偶尔跳出势阱做大幅高速运动，随机共振的影响较弱，整体动态响应较差。随着离心距逐渐增大，当H=6.45 cm时，在自调节随机共振的影响下，末端磁铁在30～50 rad/s内有足够的动能越过势垒，做大幅高速运动且可保持相对持续稳定，整体动态响应提高。当H>6.45 cm时，末端磁铁在30～40 rad/s 间尽管有自调节随机共振的影响，但不能保持大幅高速运动。仿真结果表明，压电悬臂梁在最优离心距条件下更易诱发并稳定随机共振，扩展随机共振的发生频带。

4.2.2 电压响应

为了仿真不同离心距对压电悬臂梁能量俘获的影响，本文选取RL=33.4 kΩ，根据式(19)，仿真计算电阻两端的电压，计算结果如下：

1)H=6.45 cm为最优离心距时，此时压电悬臂梁的瞬时电压如图8所示。

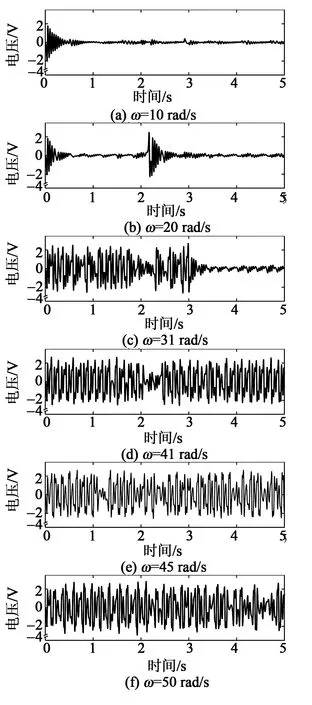
图8 最优离心距时不同旋转频率的瞬时输出电压

2) 取H分别为0，4 cm，6.45 cm，7 cm，8 cm，此时压电悬臂梁的电压均方根值如图9所示。

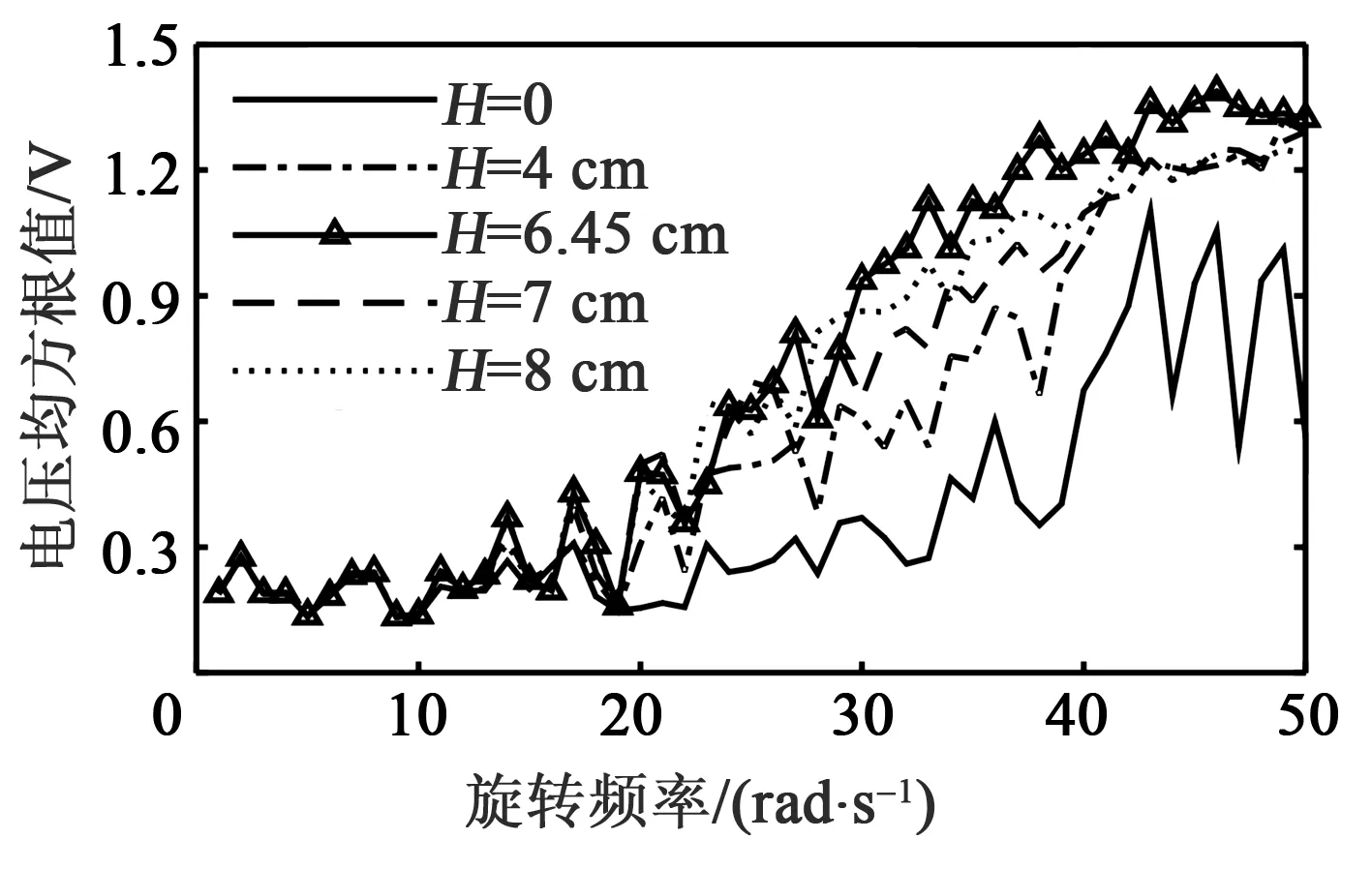
图9 不同离心距下输出电压均方根值

图9中每个点的数据为经过平均模拟时间100 s，固定旋转频率，每个离心距模拟40次后，计算出平均输出电压均方根值。设有效电压为0.9 V，随着离心距增加，电压均方根值同时增加。当H=6.45 cm时，压电悬臂梁的电压均方根值在30～50 rad/s内达到最大值。随着离心距继续增大，电压均方根值开始降低。由图8可看出，在30～50 rad/s内电压幅值显著提高。上述分析结果与位移和速度响应分析结果相同。在30～50 rad/s，最优离心距(H=6.45 cm)下自调节随机共振频率使压电悬臂梁的输出电压显著提高，拓宽频带比约为40%，同时其输出电压高于其他离心距下的输出电压。

5 结论

本文建立了旋转能量采集器的系统动力学模型，通过Kramers逃逸速率与旋转频率的非线性匹配关系，从理论上得到了最优离心距。对系统进行动力学特性仿真研究，得到不同离心距情况下采集器的响应情况，为压电悬臂梁在低频下的模型优化提供了一定的理论依据。研究表明：

1) 压电悬臂梁安装在轮胎上并处于旋转状态时，系统的等效刚度系数是关于旋转频率的函数，且系统的随机共振频率呈现可调特性。

2) 建立旋转频率与Kramers逃逸速率的优化匹配机制，可获得最优离心距及其频率匹配点理论模型。

3) 低频区域自调节随机共振在最优离心距条件下，更易诱发并稳定随机共振，扩展随机共振的发生频带，有效提高系统输出响应，从而提升能量俘获综合性能，为自调节随机共振在旋转振动场景中的进一步广泛应用提供了通用理论技术支撑。