泰勒公式应用的实例探讨
王仲梅 ,孟献青,何国满
(1.湖南工商大学数学与统计学院,湖南长沙 410205;2.山西大同大学数学与统计学院,山西大同 037009)
定理1(带有皮亚若型余项的泰勒公式)若函数在f(x)点x0存在直至n阶导数,则

定理2(泰勒定理)若函数f(x)在[a,b]上存在直至n阶的连续导数,在(a,b)内存在(n+1)阶的导数,则对于任意给定的x,x0∈[a,b],至少存在一点ξ∈(a,b),使得
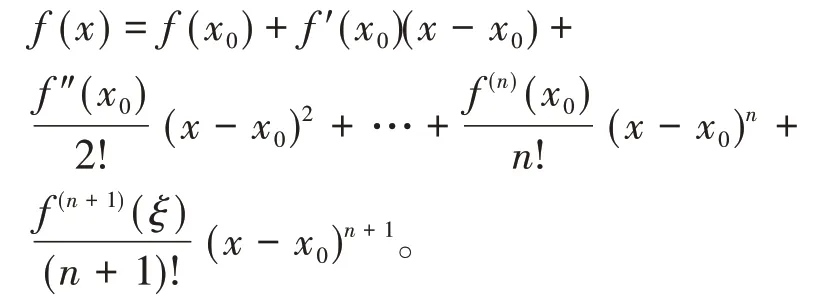
这里ξ是x0与x之间的某个值,该公式称为带有拉格朗日型余项的泰勒公式。
(1)当n=0 时,带有拉格朗日型余项的泰勒公式即为拉格朗日中值公式f(x) -f(x0)=f´(ξ)(x-x0);
(2)在x0=0 展开的泰勒公式,也称为麦克劳林公式;
(3)定理1的条件要求低,仅用于x0邻域,例如讨论x→x0时的极限,确定无穷小的阶,考察局部极值问题等;定理2 的条件要求相对高些,这个公式为整体泰勒公式,可用于讨论区间[a,b]上函数的整体性质,证明函数或者导数存在某特点等[1-3]。
1 利用泰勒公式求极限

比较(1)错误解法(等价无穷小量代换),
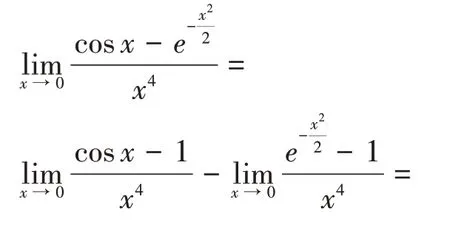
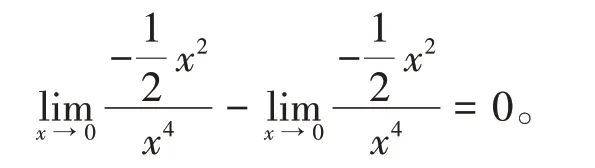
2 利用泰勒公式讨论无穷小的比较
例2设x→0 时,ex-(ax2+bx+1)是比x2高阶的无穷小,求a,b的值。
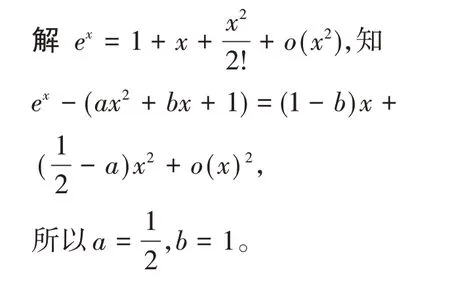
3 利用泰勒定理证明等式与不等式
例3设f(x) 在[0,1] 上二阶可导,且f(0)=f(1)=0,f(x)在[0,1]上的最小值等于-1,试证:至少存在一点ξ∈(0,1),使f″(ξ)≥8。
证明由题设存在a∈(0,1),使得f(a)=-1,f´(a)=0,利用泰勒公式
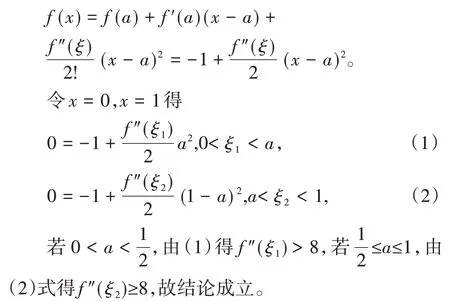
用泰勒公式时,x0的选取是关键,若证明结果中不含一阶导数时,x0可考虑选取为题设条件已知一阶导数的点或隐含为一阶导数的点。
4 利用泰勒公式讨论函数的极值
例4设f(x)在x0的某一邻域内存在连续的三阶导 数,且f´(x0)=f″(x0)=0,而f‴(x0)≠0,试证:(x0,f(x0))是曲线的拐点,而x0不是f(x)的极值点。
证明由f‴(x0)≠0,不妨设f‴(x0)>0,
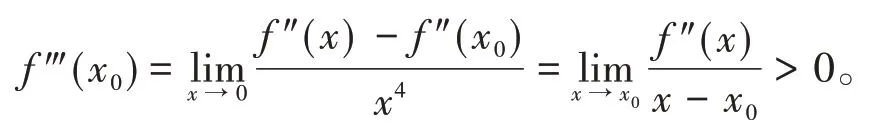
所以根据保号性存在x0的某邻域,使得>0,即x>x0时,f″(x) >0,x<x0时f″(x) <0,从而(x0,f(x0))是曲线的拐点。而
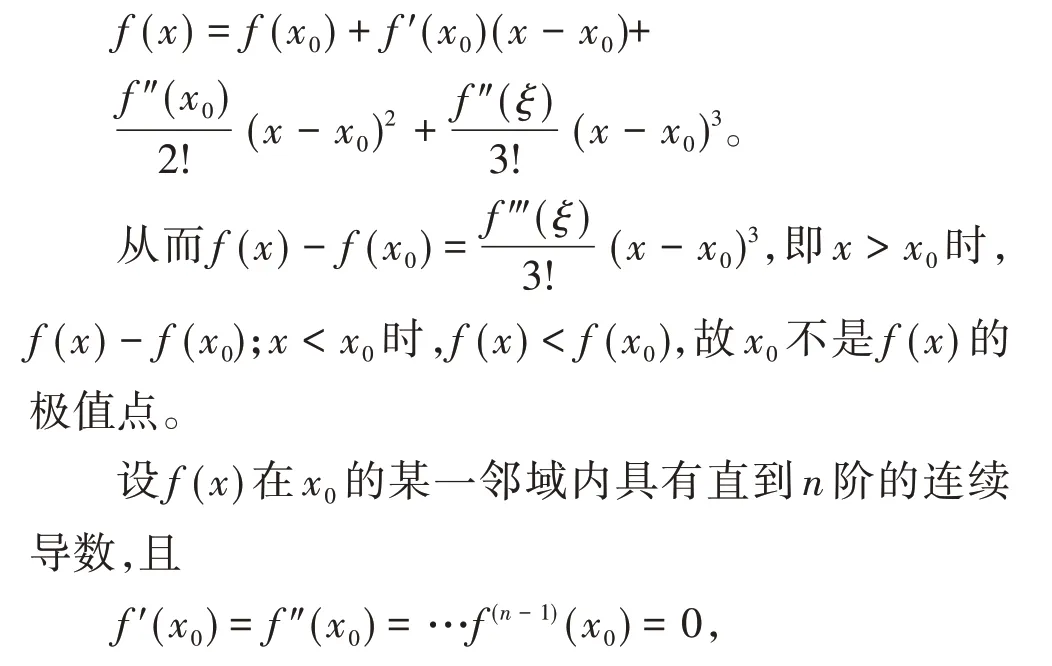
而f(n)(x0)≠0,则(1)当n为偶数,若f(n)(x0)>0 时,f(x0)为极小值;若f(n)(x0)<0 时,f(x0)为极大值(2)当n为奇数时,f(x0)不是极值。
5 与泰勒展开式中的系数比较求高阶导数
例5设y=x3sinx,求y(6)(0)。


