基于考虑居家隔离的新型冠状病毒的动力学建模与分析

梁 娟，张 伟，杨焕青，马慧莲

（1.太原工业学院理学系，山西太原 030008;2.山西大学复杂系统研究所，山西太原 030006）

2019 年12 月爆发的新型冠状病毒，是一种冠状病毒。新冠肺炎被认为是一种与SARS 病毒不同的冠状病毒，它可能是通过蝙蝠或其他宿主传播的，而突变赋予了它感染人类的能力[1]。为控制疫情的继续蔓延，中国政府于2020 年1 月23 日对武汉采取了封城举措，全国控制人口流动，这有效的减缓了疾病的发展态势[2]。2019 年12 月12 日，中国卫生健康委员会在武汉确诊的第一例冠状病毒感染以来，至2020 年3 月16 日，中国共确诊病例81 000 余例。而世界100多个国家现在也面临着挑战，并以每日数千的病例增加。该冠状病毒的传播性和危害性已经严重影响到了人类的安全。对该病毒的研究和预测已尤为重要。

为了更好地控制和预测新型冠状病毒的传播，国内外很多科研工作者已经对该病有了很多研究。Chinazzi 等人使用一个全球超人口疾病传播模型来预测旅行限制对该病毒在国内和国际传播的影响。研究表明，在武汉的旅游禁令开始时，中国大多数城市已经有了受感染的人群，中国大陆的整体疫情进展推迟了3～5d，在国际范围内的影响更为明显[3]。一些建模工作者给出了新的模型预测疾病的流行势态[4]。黄森忠等提出了符合实际的SEIR模型，并通过模型对COVID-19进行了预测，同时评估了控制策略的效率[5]。将干预效果进行参数化加入模型中，更有助于对疾病的预测[6]。一些学者根据流行病学分析方法将2019 年的新冠肺炎与2003 年的SARS 做了比较，建立了多元函数模型，得到了新冠肺炎的致死率要低于SARS、发病主要集中在30～50 岁之间的结论。

自新冠肺炎疫情暴发以来,中国政府全力抗击疫情,使得新冠疫情在我国得到了有效的控制。主要考虑居家隔离对新型冠状病毒传播的影响。以上海市为例，研究了新冠肺炎疫情在上海市的传播动力学。通过运用最小二乘法对SEIR模型中的传染率系数进行了参数估计，并对基本再生数进行了灵敏度分析。对研究疾病发展和控制病毒传播给出了一定的理论指导，同时也证明了我国政府在抗击疫情中采取的正确有效的措施。

1 动力学模型构建

主要考虑到COVID-19 通过人与人之间传播，且该病潜伏期具有传染性。将人群分为两大部分：一部分为“出门的人群”（活跃度较高的人群即活跃态的人群），S1(易感者)，E1(处于潜伏期的人群),I1(染病人群)；另一部分为“居家自行隔离的人群”(活跃度较低的人群即隔离状态的人群)，S2，E2，I2。R为移出的总的活跃人群与不活跃人群。模型假设如下：

(1)主要考虑采用居家隔离措施对新型冠状病毒传播的影响，不考虑自然出生和死亡；

(2)假设S2只要处于“隔离”状态就不会被传染。

根据以上分析，我们给出了这几类人群的仓室流程图，如图1所示。

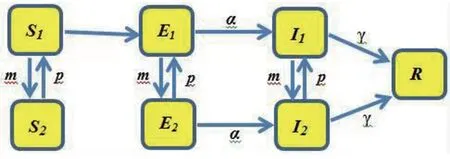
图1 疾病传播流程图

动力学模型

其中β1为潜伏期的传染率；β2为染病者的传染率；α为潜伏率，1/α为潜伏期；γ为移出率；m为从活跃度较高的人群进入活跃度较低的人群的转化率；p为活跃度较低的人群进入活跃度较低的人群转化率.以上考虑的时间都以天为单位。

定理1设系统(1)的初始条件S1（0），S2（0），I1（0），I2（0），E1（0），E2（0）,R（0）为非负的，则∀t＞0，系统(1)的解的正不变集和吸引域为Γ={(S1,S2,…,R) ∈R+|0≤S1,S2…,R,S1+S2+…+R≤N}。

证明将(1)的7个方程相加得

可知N为常数，即总人口保持不变。从而有(S1+S2+…+R)≤N。

因此，具有非负初始条件的系统(1)的解将始终在集合Γ中。给出基本再生数R0[7]

将无病平衡点带入(2)式可求Jacobian矩阵为：

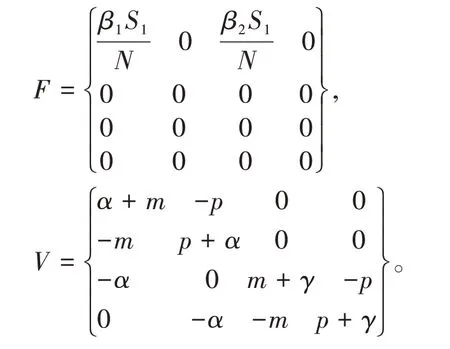
通过计算，得到基本再生数为：

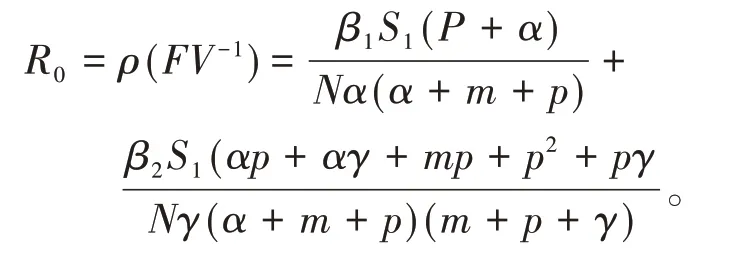
2 主要结果

2.1 参数估计

以上海市为例，对模型(1)进行了参数估计。该市于2020 年1 月20 日出现感染者病例，考虑到正值春节前夕，绝大部分人处于非隔离阶段。分如下几步将模型中初值和参数的数据给出：

(I) 根据上海市卫健委数据可知，在1 月20 日首次出现两例病例，过五天后即1 月24 日为除夕，所以平均5d 后进入不活跃状态，但在其中部分人有工作的需要，假设有60%的人居家隔离，所以m=1/5*0.6=0.12。根据当时数据得，一个多月后上海市没有新增病例（除国外输入），基本解除隔离，在不活跃人群平均停留时间为40 d，所以p=1/40。

(II) 上海市人口共有24 237 800 人（数据来源上海市统计局），根据上述分析，居家隔离比例为m=0.12，所以S2=24 237 800 × 0.12=2 908 536。

(III)根据中国疾控中心文件《新型冠状病毒肺炎公众防护指南》(第二版)，潜伏期为1～14 d，多为3～7 d，我们取3 d，则α=1/3。根据上海市卫健委数据，第二天的确诊累积病例有9例，第三天的确诊累积病例有16例，所以潜伏期的人数不超过16，但多余9。假设潜伏 期人数 为10，其中E1=5，E2=5。因此，S1=24237800 -2908536 -10 -1=21329 252。

为了估计模型(1)中的参数β1和β2，通过最小二乘估计对上海市2020 年1 月20 日-2020 年2 月19 日的染病者累计确诊人数进行了拟合（含外来人口，不含境外输入）并对2020年2月20日-2020年3月14日累计病例数进行预测。上海市累计确诊人数的拟合结果和预测结果由图2 给出。从图2 可以看出，模拟结果符合真实的数据走势，说明所研究的模型以及通过拟合得到的参数值可以较好的反应真实的疾病发展态势。同时从该图可以得到，在30 d 后，疾病预测结果与实际相符。累积病例数并无增长，表明了疾病得到了较好控制。

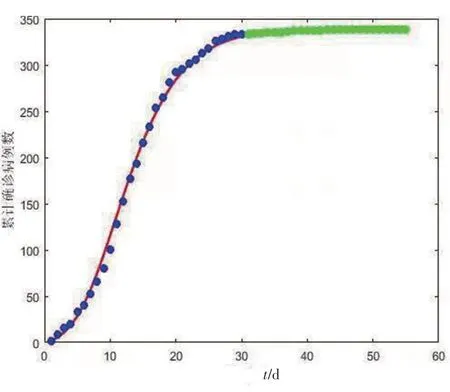
图2 上海市累计确诊病例拟合结果与累积确诊病例的预测结果

2.2 对各参数的灵敏度分析

进行灵敏度分析，以确定对基本再生数影响较大的参数[8-9]。使用Matlab 软件，计算了R0和参数之间的偏秩相关系数(PRCC)和对应值。偏秩相关系数(PRCC)反映在控制其他变量时，两变量之间的相关关系，其计算公式如下：

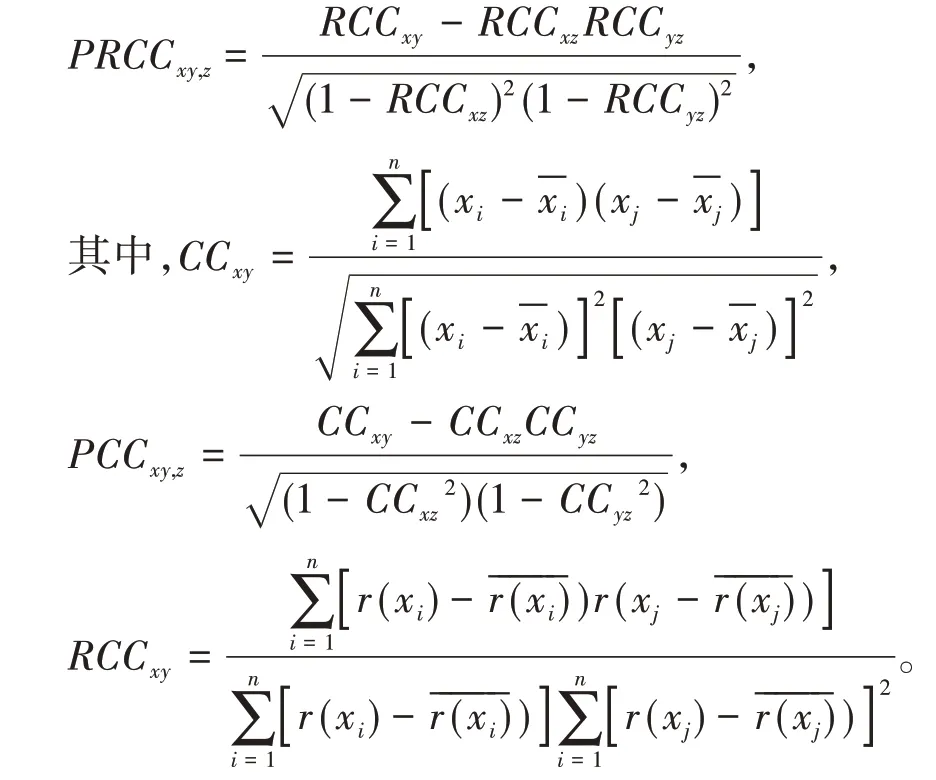
图3 给出了模型(1)中各个参数与R0的相关性。通过图3 可以看出，影响疾病传播较大的参数有m，α，β1和β2，且参数m的影响最大。参数β1和β2对R0有正的影响，说明随着β1和β2的增加，R0会增加。反之，m和α对R0有负的影响，即随着m和α的增加，R0会减少[10]。通过灵敏度分析，得出结论

图3 模型（1）中各个参数与基本再生数的相关性

(1)尽量增大参数m的值，扩大“不活跃人群”的比例，即采取居家隔离，减少社交活动等措施是最有效的控制新型冠状病毒的措施之一。

(2)尽量降低传染率β1和β2，避免与感染者和潜伏者的有效接触。本着“早发现早隔离”的原则，尽量切断传染源是降低传染率的有效方法。比如，可以通过外出戴口罩降低有效接触。

3 结论

通过考虑带有居家隔离的SEIR 动力学模型,以上海市为例，研究了新型冠状病毒在该地区的传播情况。通过数学分析，得到了基本再生数R0。由已有的上海市55 d 的感染者确诊病例数，通过最小二乘法对模型(1)中传染率进行了参数估计，得到了最优的符合实际情形的传染率。最后将参数关于基本再生数进行了灵敏度分析并且模拟了各个参数对染病者累计确诊病例的影响。

模拟结果发现，传染率β1和β2、活跃人群向不活跃人群的转化率m以及潜伏期β1，对疾病传播有较大的影响。其中，参数m的影响最大。所以，尽量减少传染率同时尽量扩大不活跃人群的比例是控制疾病的有效方法。所以，在实际中应当采取居家隔离策略，尽量避免外界接触，减少社交活动。同时为了降低传染率，应当对疾病早发现早隔离，尽早切断传染源。出门带口罩也可很大程度降低被感染的机率。

对新冠肺炎疫情的控制提供了一定的指导意义，同时也证明了中国控制疫情采措施的有效性。在新型冠状病毒传播的过程中，还会受到很多因素的影响，比如：社交距离、环境、扩散、年龄等[11]。目前，世界很多国家疫情还未得到控制，在未来的工作中，我们会将这些因素加入传染病模型中，研究它们对疾病的影响，进一步探讨新型冠状病毒的传播动力学。