三角形h-BNC/石墨烯复合异质结的整流特性
王丽华,丁秉钧
(1.山西大同大学物理与电子科学学院,山西大同 037009;2.西安交通大学理学院,陕西西安710049)
Aviram 和Ratner 在1974 年首次提出了分子整流器的概念[1],此后由于它在分子存储和逻辑电路中的广泛应用而引起了广泛关注。Li 等的研究[2]发现,金属原子钝化TG/氢原子钝化TG 异质结的整流方向与非金属原子钝化TG/氢原子钝化TG 的异质结相反。Deng 等的研究[3]证明,通过硼-氮键连接两个TG的整流比随其尺寸增大显著提高。Ling 等人[4]计算了两个TG 通过硼、氮或硼-氮连接异质结的电子输运特性。研究结果证明,随硼-氮键增加,整流比和负微分电阻效应都减小。
实验上已经成功制备出了单层六方硼氮(h-BN)纳米片[5],它是类似蜂窝晶格中硼和氮原子交替的类石墨烯绝缘材料。事实证明,h-BN 中硼和氮原子也会形成非常强的sp2键,从而形成与石墨烯类似的平面结构。值得注意的是,Gao 等人[6]在钛(111)表面成功生长了h-BNC。Qiu 等人[7]提出扶手椅型h-BNC的整流特性和负微分电阻效应可通过接触原子及元素比例调节。此外,在边界类型改变的锯齿型h-BNC 中观察到了整流行为,其电子输运特性与边界类型密切相关,而与杂化纳米带的宽度无关[8]。文章采用密度泛函理论(DFT)结合非平衡格林函数方法(NEGF),研究了由不同顶点原子和不同元素比例的三角形h-BNC和TG构成异质结的整流性能。
1 模型和计算方法
如图1 所示,构建的异质结由三角形h-BNC 和TG 组成,每个模型都可分为左电极(LE),散射区(SR)和右电极(RE)三个区域,这种异质结具有最小的接触界面,可有效防止三角形h-BNC 和TG 之间的分子态混合。其中蓝色,粉色和灰色小球分别代表氮原子,硼原子和氢原子。为了保持稳定性,所有边界原子的悬挂键都被氢原子饱和。两个半无限扶手椅型石墨烯(AGNR)电极都由沿输运方向两个重复的AGNR 超原胞构成。考虑到分子和电极之间的屏蔽效应,散射区在靠近电极处包含两个AGNR 晶胞。h-BNC 中的元素比例用P=N硼+氮/N硼+氮+碳表示,其中N硼+氮表示硼原子和氮原子数目之和,N硼+氮+碳表示硼原子、氮原子和碳原子总数。如图1(a)~(d)所示,四个模型分别命名为E1(p=6/22,氮-碳键),E2(p=13/22,氮-碳键),F1(p=6/22,硼-碳键)和F2(p=13/22,硼-碳键)。为了消除异质结与其邻近镜像之间发生相互作用,在x和y方向都添加了15Å的隔离层。

图1 三明治异质结构模型图
文章涉及的计算均使用基于DFT 结合NEGF 的Atomistix Toolkit (ATE) 程序包完成[9]。该方法已经被很多研究人员采用,他们的计算结果与实验数据很符合[10],充分说明了该方法的可靠性。输运计算中,电子采用Troullier -Martins 标准守恒赝势描述,交换相关势采用局域密度近似(LDA)。平衡密度矩阵采用等值线积分法计算,非平衡密度矩阵在虚部为0.001 eV 的直线上进行数值计算。为实现计算效率和精度的平衡,所有原子均采用SZP 扩展波函数,电子温度固定在300 K,k-mesh 在x、y、z方向分别采用1、1、100,其中z为AGNR 的周期方向,截断能和密度矩阵的收敛标准分别设置为200 Ry 和10-4。器件的电子和输运特性使用开放边界条件描述。首先松弛每个模型的原子位置,直到作用在每个原子上力的绝对值小于0.05 eV/Å 。平均费米能级(EF),即左右电极化学势的平均值,设置为零。在自洽计算中,电荷密度沿半圆积分超过400个能量点。
自洽计算收敛后,通过双探针系统的电流通过类Landauer 公 式[11]I=T(E,Vb)dE计 算,其中,T(E,Vb)是在能量E 和偏压Vb时的透射系数,μL(μR)是左(右)电极的电化学势,它们的差值为μL-μR=eVb。因此,电流仅由偏压窗内透射系数的积分确定。左(右)电极为阴(阳)极时产生正电流。否则,就会产生负电流。
2 结果与讨论
电流-电压(I-V)曲线(偏压为-2.2~2.2 V)如图2所示。首先,四个模型都具有相同的特性,即在-1.8~1.8 V 范围内电流被完全抑制,而当偏压的绝对值大于1.8 V时才产生了电流。这个结果与之前报道的不同顶点原子掺杂的两个TG 相吻合[12]。其次,对模型E1 和E2,正偏压电流总大于负偏压电流。而模型F1和F2 表现出了相反的特性,即负偏压电流总大于正偏压电流。最后,模型E2 和F2 的I-V曲线非对称性比其它两个模型更明显。这种非对称性用整流比表示,如图2(a)和(b)图所示。对于模型E1和E2,整流比定义为正偏压电流与负偏压电流的绝对值之比,即RR=I(V)|I(-V) |。因此RR>1(RR<1),表示正向(反向)整流。而对于F1 和F2,整流比通过RR=|I(-V)|I(V)计 算,RR>1(RR<1) 表示反向(正向)整流。此外,从图2(a)和(b)图发现了两个有趣的整流特性:①整流方向取决于h-BNC 的顶点原子类型(氮或硼)。顶点原子为氮时的E1 和E2 表现出正向整流特性,而顶点原子为硼时的F1 和F2 表现出反向整流特性;②正向或反向整流比与元素比例相关。模型E2(F2)中的元素比例较大,正向(反向)整流效应明显比E1(F1)的强。综上所述,h-BNC 的顶点原子类型可控制异质结的整流方向,而具有相同顶点原子异质结的整流比可通过元素比例调节。

图2 I-V特性曲线
为了理解上述四种模型的整流特性,计算了随能量和偏压变化的透射谱,如图3 所示,其中EF如上所述设置为零。一般认为透射谱是器件量子输运特性最直观的表征。从图3 可以看到,随偏压增加,透射谱发生了很大变化。对于模型E1,正偏压时偏压窗内总会出现一个大透射峰,而负偏压时只在EF附近出现了一个很小的透射峰,导致正偏压电流总是大于负偏压电流,从而产生了正向整流。模型E2 与E1 的情况相似,因此E2 仍呈现正向整流,但由于负偏压时偏压窗内的输运系数接近零,导致其整流比明显大于模型E1。模型F2 负(正)偏压时偏压窗内的透射谱明显大(小)于F1,带来F2较大的反向整流比。
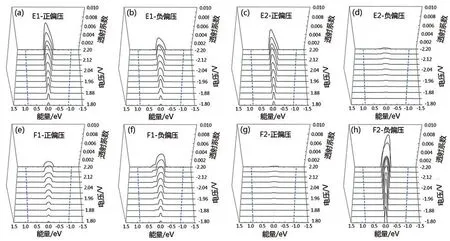
图3 不同偏压下的透射谱
为了明确不同轨道对整流特性的贡献,图4展示了± 2 V 时SR 区域的总态密度(DOS)和投影态密度(PDOS)。对于所有模型,观察到DOS 峰值主要来自p轨道的贡献,即s、d或f轨道对总DOS 的贡献很小或没有贡献。值得注意的是,DOS 和PDOS 强烈依赖于偏压的极性,这有助于在纳米器件中实现整流效应。

图4 ±2 V时的DOS和PDOS
对于模型E1和E2(F1和F2),p轨道在正(负)偏压时的总DOS和PDOS 峰值大于负(正)偏压的值,因此,模型E1和E2(F1和F2)表现了正向(反向)整流特性。
3 结语
应用DFT 结合的NEGF 的理论,研究了三角形h-BNC 和TG 夹在两个AGNR 电极之间形成的异质结构的电子输运性质。结果表明,通过改变顶点原子类型和元素比例p(P=N硼+氮/N硼+氮+碳)可有效调节构建体系的整流效应。当h-BNC 和TG通过氮-碳对结合时,出现了正向整流行为。而当h-BNC和TG 通过硼-碳对结合时,观察到了反向整流行为。此外,h-BNC中的元素比例P越大,正向(反向)整流比越大。

