增长区域上扩散的昆虫捕获模型解的渐近性
梁建秀 ,罗 芳,石漂漂 ,张雪霞
(1.晋中学院数学系,山西晋中 030619;2.山西大同大学数学与统计学院,山西大同 037009)
在20 世纪50 年代初,Skellam[1]就将扩散引入到生态模型中用来研究种群的渐近行为,之后反应扩散系统被广泛应用于描述种群动力学中生物体空间扩散的影响,Marray 等在文献[2]中研究了一类简单的非线性反应扩散昆虫模型

其中u(x,t)表示昆虫的种群密度,d为扩散系数,a,b分别为种群的内禀增长率和种内竞争率,q为正的常数,Ω ∈ℝn(n≥1),且具有光滑边界∂Ω,齐次Dirichlet边界条件表示边界没有种群传播,对于模型(1)有如下结果。
定理1设μ1为下列问题的主特征值

(Ⅰ)若a≤dμ1,则模型(1)有唯一非负稳态解u=0,且该解是全局渐近稳定的。
(Ⅱ)若a>dμ1,则模型(1)有唯一非负稳态解,则模型(1)有唯一正稳态解u=u*(x),且该解是全局渐近稳定的。
当q=1 时,问题(1)就是经典的具有扩散的Logistic 方程,对该问题已经得到了广泛而深入的研究。通常人们通过反应扩散模型来刻画生态现象时,大多数考虑的空间区域都是固定的,近年来,区域的增长对种群或传染病的发展演化的影响引起了较多学者[3-9]的关注。文献[3]分别在区域有限增长和区域无限增长情形下研究了具有扩散的Logistic模型解的渐近性态;文献[4]在问题(1)的基础上考虑了区域增长,建立了增长区域上的昆虫扩散问题,对其解的渐近性态进行了讨论。考虑到可再生资源的持续开发和利用,很多学者又关注并研究了单种群的捕获模型[5]等,文献[6]在周期演化区域上对单种群的Logistic捕获模型的动力学进行了分析,受已有工作的启发,将研究增长区域上一类具有捕获的反应扩散的昆虫模型。
对于模型(1),引入捕获项,则得如下反应扩散的昆虫模型
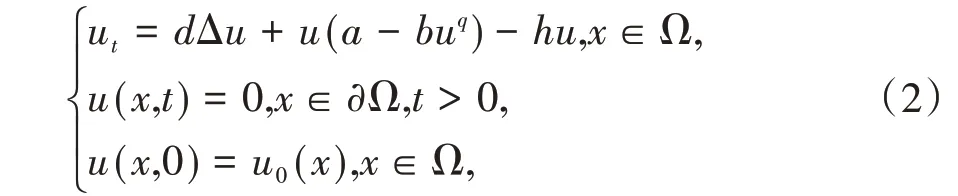
这里h为捕获能力系数,hu表示捕获数,其它参数的生物意义同模型(1)。
类似于文献[4],设Ω(t)为一个随时间而变化的区域,其边界为∂Ω(t),对于任意一点
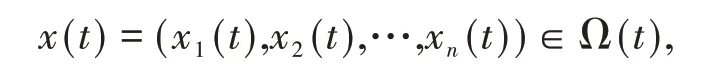
假设u(x(t),t)为种群在时刻t和位置x(t)处的密度,根据质量守恒定律,由Reynolds 输运定理,再利用Fick扩散定律得


其中u0(x(0))为正的有界函数,Ω(0)为初始区域,假设区域Ω(t)的变化为各向同性,即当时间t增加时,区域Ω(t)在所有方向上以相同比例进行变化,即数学上表示为
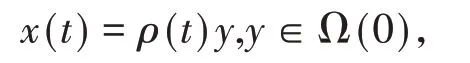
其中∂Ω(0) ∈C2,ρ(t)称为增长函数,在[0,+∞)上连续可微,满足ρ(0)=1,对所有为初始区域Ω(0)上的空间坐标,由于模型(3)中含有对流项和稀释项,对解的性态研究有较大困难,为便于研究模型(3)解的性质,类似于文献[4]的方法,利用Lagrangian坐标变化,将一个连续演化的区域Ω(t)转变为一个固定的区域Ω(0),即令u(x(t),t)=v(y,t),这里x(t)=ρ(t)y,经计算则有

则模型(3) 就转化为固定区域Ω(0)上的具有捕获的昆虫扩散模型

模型(4)是要进一步研究的新的具有捕获的昆虫扩散模型。
为了研究模型(4)解的渐近性,首先给出模型(4)的上解与下解的定义。




由以上讨论可知,区域的增长函数ρ(t),扩散率d及捕获率h等对种群的生存都存在一定的影响。

