含预填块复合材料帽型单筋板弯曲性能研究

戴征征，余章杰，张 琪，陆方舟，蔡登安，周光明

（南京航空航天大学机械结构力学及控制国家重点实验室，南京 210016）

复合材料以其卓越的力学性能及减重优势在飞机结构中得到广泛应用［1］。复合材料加筋板是一种典型的复合材料整体化结构，相比于单一的复合材料层合板，加筋板通过在层合板表面添加不同类型的筋条，可使结构的极限承载能力大幅度增加［2⁃3］。加强筋条的形式有很多种，如T 形、L 形、I 形及帽形［4⁃5］，其中帽型加筋结构因其具有天然的损伤容限性能高等优良特点，而被大量应用于机身、后压力框等结构中［6］。帽型筋条的切面尺寸较大，其两腹板通过凸缘与蒙皮相连形成一个闭合剖面，具有很高的受压稳定性，可以承受重载，能够满足多种载荷传递路径要求［7］。但是，在服役过程中，机身桶段帽型加筋结构几乎一直承受复杂弯曲载荷［8］，相比于其轴向强度、刚度，帽型筋板结构弯曲性能较差，帽板和底板连接处易发生脱粘失效［9］，同时为与其他结构相连接，帽型筋板在使用环境中经常需要在沿筋条打入销钉等连接固定件，导致筋条和蒙皮在此处更容易出现损伤。这不仅限制复合材料的力学优势的发挥，也对飞机安全构成极大的威胁［10⁃11］。

针对二次胶接复合材料帽型筋板结构，孙晶晶［12］通过四点弯曲试验模拟了帽型筋板受后屈曲载荷时的蒙皮/筋条界面性能，建立了渐进损伤模型，分析了蒙皮/筋条界面的脱粘机理和失效过程；Turon 等［13］基于内聚力模型研究了复合材料加筋板脱粘失效问题，将有限元软件模拟结果与试验结果进行比较，两者结果相近；王力立等［14］对复合材料帽型筋结构四点弯曲试验进行了有限元模拟，并对复材板损伤过程进行了模拟，筋条破坏方式均为加载点的压塌破坏。以上帽型筋结构数值仿真研究中，筋条和蒙皮的有限元模型均简化为壳单元模型，对复材板的初始失效判定均采用ABAQUS 中内置的二维Hashin 准则，模型与实际结构有所差别。

针对不同成型工艺对帽型筋板结构拉、压承载能力的影响，国内外也有许多研究。Kim 等［15］对不同工艺成型帽型加筋板进行拉拔试验，对比分析了共固化、共胶接和二次胶接成型加筋板工艺稳定性以及拉拔高度对承载能力的影响；徐荣章等［16］通过试验研究发现筋条与蒙皮共固化成型的三筋条复合材料帽型筋板承受轴压载荷时，结构破坏主要是由于蒙皮压缩分层断裂破坏而非筋条与蒙皮分层破坏导致。

总体而言，针对复合材料帽型加筋结构，现有的研究大多集中于筋条与复材板二次胶接成型的帽型筋，研究重点大多为筋条与底板的界面粘接强度问题。现有研究表明，二次胶接成型的帽型筋结构连接界面强度远远低于复合材料面内强度，特别是加筋结构承受弯曲、轴压载荷时，界面脱粘往往导致二次胶接帽型筋结构提前破坏［17］。但截止目前，针对筋条与底板共固化成型复合材料帽型筋板结构弯曲破坏形式仍缺乏研究。

本文研究对象为含预填块复合材料帽型单筋板的抗弯性能，帽型筋板的筋条与蒙皮采用共固化一体成型，以避免界面脱胶导致的结构承载能力下降；同时通过在结构承压部位填充短切纤维预填块（即实际使用环境中连接销钉部位等有集中载荷作用的地方），避免承载点过早被压塌导致结构承载能力下降。本文首先建立含预填块复合材料帽型单筋板三维实体单元模型，并根据Tsai⁃Wu 准则、Hashin 准则及Camanho 线性退化准则，编写相关渐进损伤子程序。通过数值模拟，对含预填块复合材料帽型单筋板弯曲破坏失效模式及损伤机制进行预测，并比较了两种损伤判据的对计算结果的影响。同时本文还研究了预填块长度对复合材料帽型单筋板承载能力的影响，为结构优化及实际应用提供参考。

1 试验与方法

1.1 分析对象参数

本文所研究的复合材料帽型筋板由筋条、蒙皮及预填块3 部分在热压罐中共固化成型［18］，蒙皮面板长420 mm，宽100 mm。共固化前，预填块四周提前裹有1 层J272⁃A 胶膜，预填块由短切纤维块和泡沫组成，中间部分短切纤维块长度为100 mm，两端的泡沫长度均160 mm，试件下方粘接有加强片。帽型筋板试验件包含两种规格，分别编号为M1、M2，均由碳纤维预浸料CCF300/BA9916⁃Ⅱ双向布逐层铺叠，固化后单层厚度为0.18 mm，蒙皮铺层数为8 层，铺层方式为［（±45°）/（0°，90°）］2s。筋条为帽型，M1 筋条铺层层数为8 层，铺层方式为［（±45°）/（0°，90°）］2s；M2 筋条铺层层数为12 层，铺层方式为［（±45°）/（0°，90°）］3s，试件具体尺寸如图1 所示。试件所选用双向布基本力学性能参数见表1，短切纤维和泡沫的力学性能参数分别见表2、3。表1 中，Eij（i，j=1，2，3）为纤维方向弹性模量，XT、YT、ZT分别为3 个方向的拉伸强度，XC、YC、ZC分别为3 个方向的压缩强度，νij、Gij、Sij（i，j=1，2，3）指3 个方向的泊松比、切变模量和剪切强度。表2 中，E1为短切纤维块弹性模量，G为短切纤维块切变模量，ν为泊松比，σ表示短切纤维强度极限。表3 中，E2为泡沫弹性模量，ν为泊松比，σe表示泡沫屈服极限。E33、G13、G23、ν13、ν23、ZT、ZC、S13和S23参考文献［10］中的数据，其余层合板、短切纤维块及泡沫力学性能参数均为同批成型的基础性能试验件试验测量所得数据。

图1 帽型筋板试件示意图Fig.1 Schematic of hat⁃stiffened panel

表1 CF3031/BA9916⁃Ⅱ材料性能参数Table 1 Material properities of C3031/BA9916⁃Ⅱ

表2 短切纤维块材料性能参数Table 2 Material properities of chopped fiber block

表3 PMI 泡沫材料性能参数Table 3 Material properities of PMI foam

1.2 数值模拟方法

试验前先通过有限元分析软件ABAQUS 建立含预填块复合材料帽型筋三维渐进损伤有限元模型，预测试件的承载能力和损伤情况。分析时将筋条帽板和蒙皮底板视为层合板，模型单层厚度为层合板固化后平均单层厚度0.18 mm，单层板本构关系参考经典层合板理论确定［19］。初始失效准则选用包含Yeh 分层失效准则的三维Hashin失效准则［20］，并与Tsai⁃Wu 失效判据［21］的仿真计算结果进行对比，三维Hashin 失效判据可区别经向拉伸失效、经向压缩失效、纬向拉伸失效、纬向压缩失效、拉伸分层失效和压缩分层失效6 种失效模式。

Tsai⁃Wu 准则是以张量形式提出的强度理论，通过增加方程中项数的方法以提高强度准则与试验结果的一致性［22］，但不能区别具体损伤形式，Tsai⁃Wu 准则认为应力空间中的破坏面存在下列形式

式中：Fi和Fij分别为一阶和二阶强度系数张量，对于复合材料单层板，可以通过破坏强度确定Fi和Fij的取值，其中F12、F13、F23计算时系数取-1，即

复合材料层合板发生失效后损伤单元的材料性能发生退化，工程弹性常数通常要做刚度折减处理，对于材料性能退化方法，已有大量的研究。本文选择Camanho 线性退化准则［23］，具体退化参数见表4。

表4 层合板刚度退化方式Table 4 Degradation mode of laminate

本文根据本构方程、三维Hashin 准则、Tsai⁃Wu 准则和完全退化模型编写UMAT 子程序研究含预填块复合材料帽型加筋板渐进损伤过程及失效机制。

采用0 厚度Cohesive 单元模拟J272⁃A 胶膜，研究预填块与复材板的粘接界面胶膜损伤情况。具 体 通 过 ABAQUS 软 件 内 置 的Traction⁃separation 法则定义Cohesive 单元的属性，通过二次应力准则判断Cohesive 单元损伤，采用基于能量的线性扩展准则来控制界面刚度的退化方式和退化速率［24⁃25］，胶膜性能参数见表5。

表5 J272⁃A 胶膜材料属性Table 5 Material properities of J272⁃A

预填块中的短切纤维视作各向同性材料，采用Mises 应力准则进行损伤判定，泡沫定义为塑性材料，采用ABAQUS 中内置的可压溃泡沫模型建模。

按照实际参数通过Catia 建立帽型筋三维实体模型，如图2 所示。实体模型装配完成后导入Hy⁃permesh 中，按实际铺层层数划分实体网并导入ABAQUS 中进行材料属性赋予、装配及单元类型选择等，蒙皮、筋条和预填块的单元类型均采用8节点、6 面体减缩积分单元，蒙皮和筋条接触部分单元采用共节点处理，蒙皮与预填块、筋条与预填块均设置0 厚度粘聚力接触。

图2 帽型单筋板三维实体模型Fig.2 Three-dimensional solid model of hat-stiffened panel

如图3 所示，建立与试验环境等直径的压头和支撑，对支撑施加位移约束，同时建立参考点与压头耦合，通过参考点施加位移载荷。

图3 有限元模型加载示意图Fig.3 Loading diagram of finite element model

1.3 试验方法

三点弯曲试验在WDW⁃E200D 微机控制电子万能试验机上进行，该试验机加载精度为0.5%，试验的固定加载速率为1 mm/min。试验夹具跨距为350 mm，压头直径为30 mm，加载点在试验件中心，支撑圆柱直径为30 mm，试验加载图如图4所示。

图4 帽形筋板三点弯曲试验图Fig.4 Three-point bending test diagram of hat-stiffened panel

为了研究含预填块复合材料帽型加筋板的变形行为，需要在特定位置粘贴应变片（花）获取应变数据并分析，尤其重点关注筋条和蒙皮中泡沫和短切纤维分界面变形情况，在这些位置增设应变片（花），应变片（花）布置位置如图5 所示，应变数据采集通过JM3813 应变测量仪，共计48 个通道。

图5 帽型筋板应变片（花）位置示意图Fig.5 Schematic of strain gauge locations of hat-stiffened panel

正式试验前进行预试，检查试验加载系统是否正常，并对试验机位移、载荷传感器进行标定。试验过程中每1 kN 进行一次应变数据采集，并及时记录试验声响，辅助分析试验件结构损伤，试验后对断面部位进行重点观察，分析结构破坏机理，每种规格的试验件包含3件，分别编号为M1⁃1、M1⁃2、M1⁃3 和M2⁃1、M2⁃2、M2⁃3。

2 结果与讨论

模型M1 和M2 的有限元仿真预测载荷⁃位移曲线及试验载荷位移曲线如图6 所示。Hashin 准则和Tsai⁃Wu 准则计算得到的极限载荷见表6，试验结果得到的极限载荷见表7。有限元仿真中两种损伤准则的载荷⁃位移曲线趋势大致相同，两种损伤准则给出了极限载荷的所在区间。其中Tsai⁃Wu 准则作为宏观失效准则，对模型的损伤预测更为保守，给出了偏安全的极限载荷，且计算量较小，工程应用上价值更高。Hashin 准则给出了具体损伤形式，便于针对损伤形式对帽型筋板结构设计和复材铺层进行改进优化，以提高承载能力。

表6 复合材料帽型筋板有限元仿真结果Table 6 Finite element simulation results of composite hat⁃stiffened panel

表7 帽型筋板三点弯曲试验结果Table 7 Three⁃point bending test results of hat⁃stiffened panel

图6 复合材料帽型单筋板有限元计算载荷-位移曲线Fig.6 Load-displacement curves of composite hat-stiffened panel by finite element calculation

试验件M1⁃1 和M2⁃1 均加载至第1 次掉载即停止加载，留待切剖进一步观察试验件内部损伤破坏情况。试验结果载荷⁃位移曲线重合度较高，极限载荷离散系数较小，说明了试验具备较好的可重复性。 试验件M1⁃1、M2⁃2 极限载荷分别为13.62 kN，略小于同组其他试验件，可能是试验件加工误差导致。

同时，对比仿真和试验的载荷位移曲线和极限载荷，有限元仿真所预测的结构承载能力和结构整体刚度与试验结果大致相同，说明所建立的有限元模型的准确性。

2.1 有限元结果

如图7 所示，以模型M1 的Hashin 准则作为损伤判据的计算结果为例，重点关注达到极限载荷前的载荷⁃位移曲线。

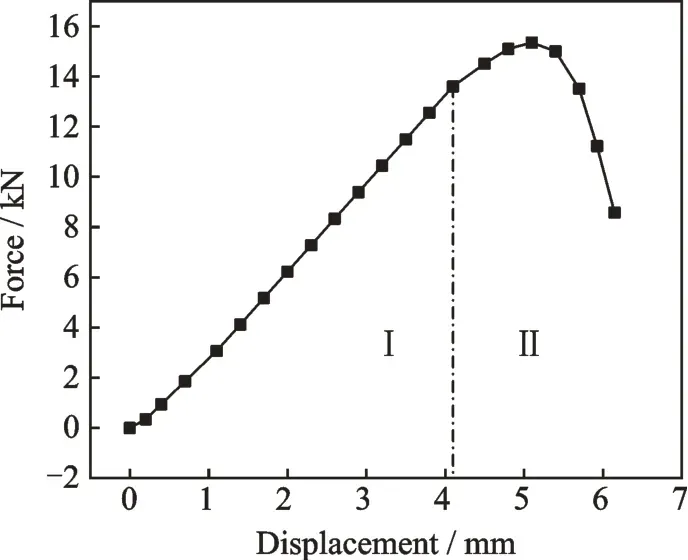
图7 M1 模型Hashin 准则有限元计算载荷-位移曲线Fig.7 Load-displacement curve of M1 model (Hashin crite⁃rion)

该部分的载荷位移曲线可以分为2 个阶段：第1 阶段，载荷随位移呈线性关系，随着位移增加，载荷迅速升高；第2 阶段，曲线斜率出现减小，载荷仍随位移增加但增速变缓，当位移达到5.1 mm，载荷增至极限载荷15.15 kN 后，载荷迅速降低。

结合载荷位移曲线、损伤变量状态及应力应变云图，分析含预填块复合材料帽型单筋板的损伤过程和失效机制，第1 阶段1 方向应力S11如图8 所示，图中F指模型承载大小，U指压头向下位移量。由于短切纤维与泡沫刚度不匹配，应力主要集中在筋条短切纤维与泡沫交界处，泡沫与短切纤维应力水平较低，泡沫第1 阶段最大Mises 应力为0.69 MPa，短切纤维第1 阶段最大Mises 应力为120 MPa 左右，此时结构完整，筋条、蒙皮与短切纤维均未出现损伤，各个部位共同承载。

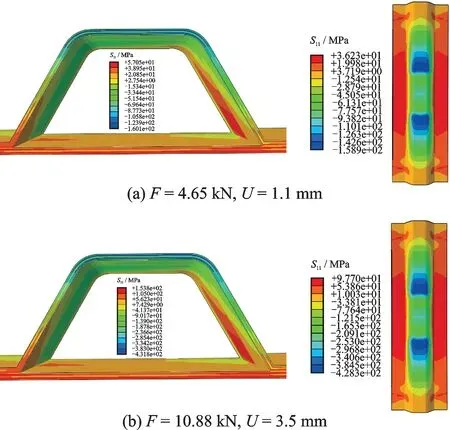
图8 模型M1 第1 阶段应力云图Fig.8 Stress contour of model M1 in the first stage

第2 阶段分为两个过程：第1 个过程对应载荷⁃位移曲线斜率降低，载荷仍缓慢增加到极限载荷，对应的筋条和胶层损伤演化过程及对应的应力云图如图9，10 所示。当位移达到4.1 mm，载荷达到13.49 kN，由于面内剪切应力S12、层间剪切应力S13、S23的共同作用，筋条的±45°铺层在短切纤维与泡沫分界处开始出现出现分层失效，同时此处的胶膜开始出现损伤并向外扩展，导致结构刚度下降，载荷⁃位移曲线斜率降低。其中SDV1～6 分别对应经向拉伸失效、经向压缩失效、纬向拉伸失效、纬向压缩失效、拉伸分层失效和压缩分层失效6 种失效模式。CSDMG 为内聚力模型损伤变量，其值不为0 时表示胶膜发生损伤；其值为1 表示胶膜完全损伤。

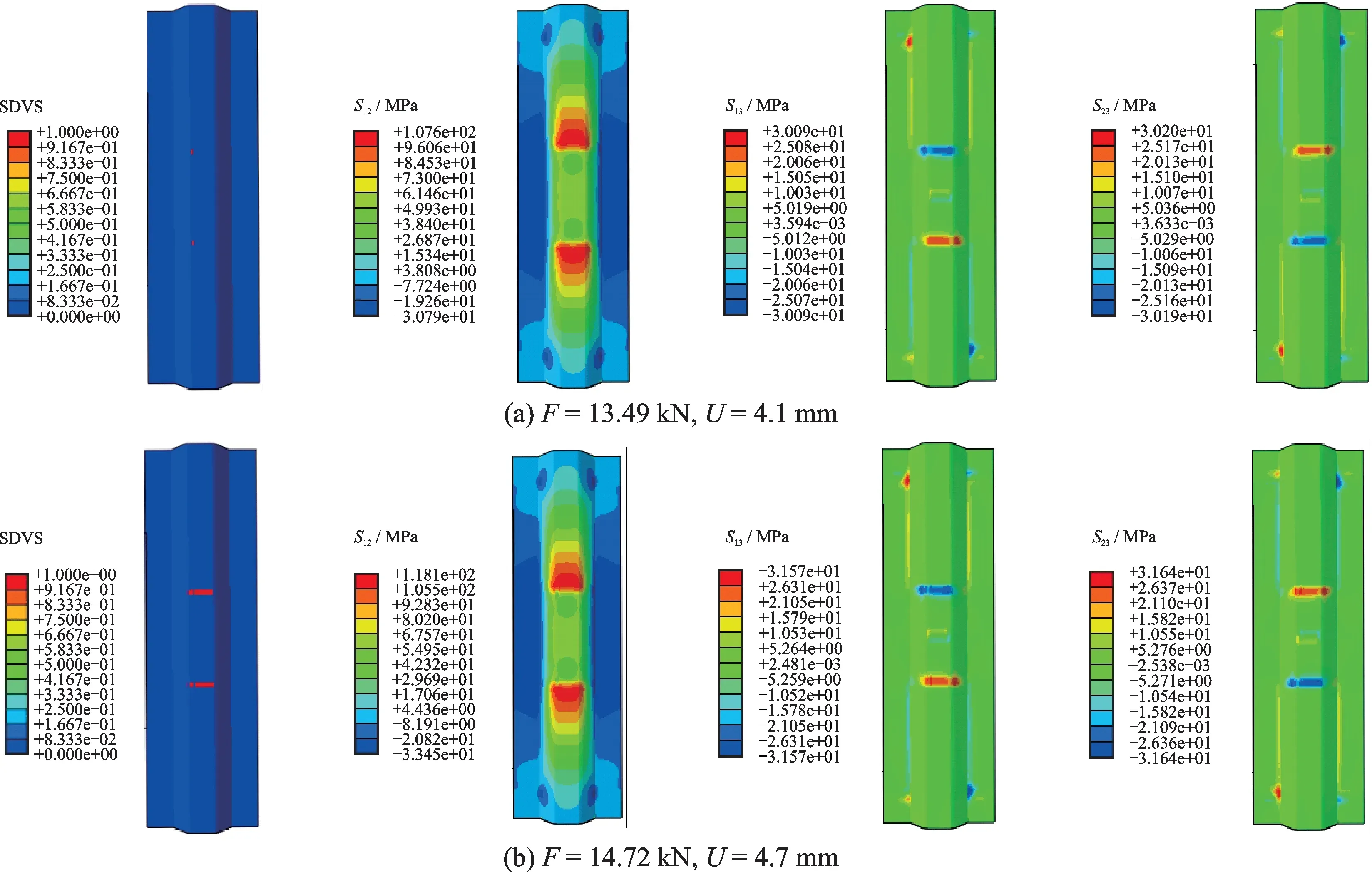
图9 第2 阶段第1 过程损伤演化过程和对应应力云图Fig.9 Damage evolution process and corresponding stress contour of the first process in the second stage

第2 个过程对应载荷⁃位移曲线达到极限载荷并迅速掉载，该过程主要出现筋条的经向压缩失效和纬向压缩失效，对应的损伤演化过程如图11 所示，筋条的应力应变云图如图12 所示。当位移达到4.7 mm，载荷达到14.72 kN，筋条（0°/90°）层泡沫和短切纤维分界处开始出现经向压缩失效并迅速向周边扩展；当位移达到5.1 mm，载荷达到极限载荷15.15 kN，筋条±45°层泡沫和短切纤维分界处出现纤维压缩破坏和基体压缩破坏，载荷迅速降低。与第1 个过程分层失效相比，经向压缩失效与纬向压缩失效扩展更为迅速，且出现失效后模型载荷⁃位移曲线很快到达载荷最大值，说明纤维压缩对筋条结构破坏起到了决定性的作用。

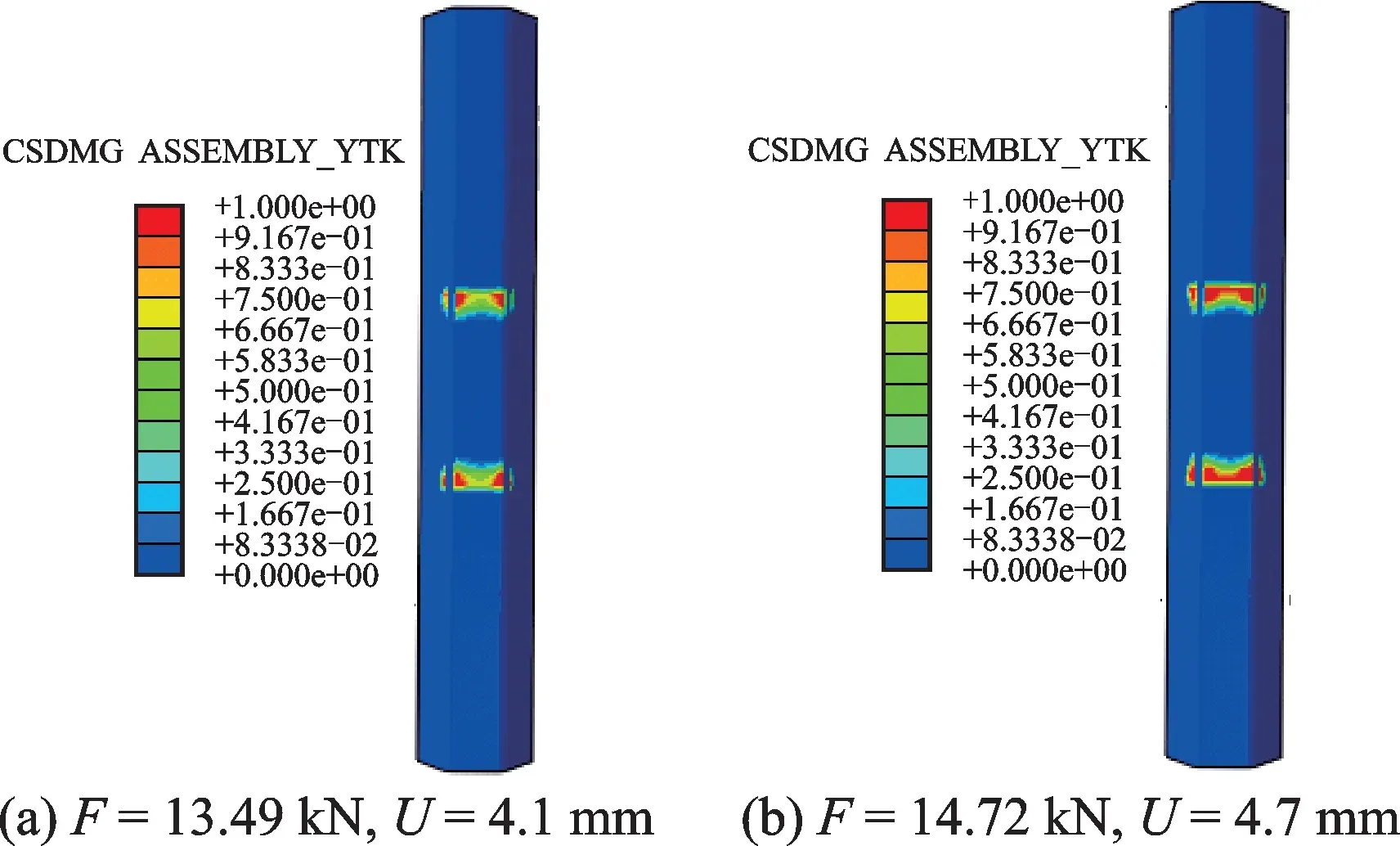
图10 胶膜损伤扩展云图Fig.10 Contour of damage evolution for adhesive layer

图11 筋条第2 阶段第2 过程损伤演化过程Fig.11 Damage evolution process of the second progresss in the second stage of the rib

图12 筋条第2 阶段第2 过程应力云图Fig.12 Stress contour of the second process in the second stage of the rib

筋条“压断”第1 次掉载后，随着加载位移继续增加，结构仍能继续承载，蒙皮成为主要承载结构，此过程蒙皮的应力云图如图13 所示；当位移增至15.5 mm，载荷达到8.95 kN，出现第2 次掉载，蒙皮出现纤维拉伸断裂，结构完全破坏，计算终止，具体损伤情况及应力云图如图14 所示。

图13 蒙皮第3 阶段应力云图Fig.13 Stress contour of the skin in the third stage

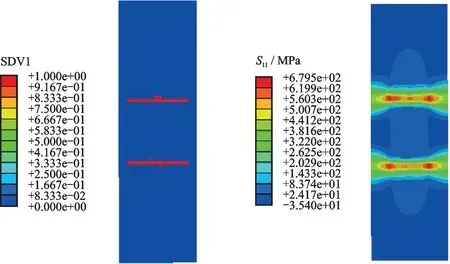
图14 蒙皮破坏位置及对应应力云图Fig.14 Damage location and corresponding stress cloud of skin

仿真全过程短切纤维预填块仅在与泡沫分界处出现细微损伤，承载状况良好，第4 阶段短切纤维预填块损伤情况及应力云图如图15 所示。

图15 短切纤维块损伤情况及应力云图Fig.15 Damage situation and stress contour of chopped fi⁃ber block

2.2 试验结果

以M1⁃3 为例，分析由载荷⁃位移曲线可以看出：起始阶段，载荷随位移呈线性增长，在达到极限载荷前未出现任何波动，试验件未发生损伤。当位移达到4.95 mm，载荷为15 kN 时，筋条在靠近短切纤维与泡沫交界处发生断裂破坏，载荷剧烈下降至4.25 kN。但观察试验件，筋条与蒙皮未出现分层现象，蒙皮在此时未出现明显损伤，可以继续承载。继续下压压头，载荷在4 kN 附近保持稳定，当位移达到13.95 mm，载荷出现突降，蒙皮短切纤维与泡沫交界处断裂破坏，筋条与蒙皮仍未出现分层现象。

利用高速切割机，沿短切纤维与泡沫分界处的截面对试验件进行切开，通过KH⁃7700 数字显微镜对切割面内部损伤情况进行观察，放大倍数为5倍。如图16 所示，筋条靠内铺层在短切纤维与泡沫分界处出现分层损伤，胶膜出现局部脱粘现象，远离短切纤维与泡沫交界处的切面则未发现筋分层及泡沫脱粘现象，试验现象与仿真结果高度一致。

图16 帽型筋板试验件损伤位置剖面图Fig.16 Sectional view of damage positions of hat-stiffened panel

试验件M1⁃3 损伤破坏情况如图17 所示，试验件破坏形式与有限元仿真预测结果吻合。

图17 帽型筋板损伤破坏示意图Fig.17 Schematic of damage positions of hat-stiffened panel

2.3 分析与拓展

由试验所得的应变⁃载荷曲线可以看出，对应位置的应变数据大致保持一致，说明压头是加载在试验件中心对称面上的，试验加载和设计是合理的。M1 试验件试验所得的极限载荷平均值为14.60 kN，对应的Hashin 损伤判据仿真计算极限载荷为15.15 kN，与试验结果仅差3.6%；M2 试验件试验所得的极限载荷平均值为23.03 kN，对应的Hashin 损伤判据仿真计算极限载荷为24.13 kN，与试验结果仅差4.8%，误差均在5%以内，试验和有限元仿真的载荷⁃位移曲线趋势也大致保持一致。

对比有限元模型和试验件损伤破坏的位置，两者结构损伤破坏的位置具有高度一致性：达到极限载荷后第1 次掉载，损伤破坏的位置出现在筋条短切纤维与泡沫交界处；第2 次掉载，是由于蒙皮在短切纤维与泡沫交界处发生破坏，说明了所建立的渐进损伤有限元模型的可靠性。

为了验证有限元计算得到的应变数据的准确性，取载荷为12 kN 时，筋条和蒙皮短切纤维与泡沫分界处具有代表性应变测点的应变数据进行对比，即在有限元模型中取22、25、38、39、44、45 测点的应变值与试验结果进行对比，如表8 所示，39 号测点应变试验与仿真差值较大，可能是该测点应变片损坏或粘接不够牢固而产生的测量误差，除去该测点外各个测点仿真和试验应变数据大致吻合，进一步说明有限元建模的可靠性。

表8 部分测点应变值与仿真值对比Table 8 Comparison of strain values and simulated val⁃ues

试验验证了渐进损伤有限元模型的准确性后，本文还通过有限元模型继续研究了短切纤维块长度对帽形筋承载能力的影响，不同纤维块长度的有限元模型及数值模拟破坏载荷如表9 所示，极限载荷⁃短切纤维块长度曲线见图18。

表9 不同纤维块长度模型参数及极限载荷Table 9 Model parameters and ultimate loads of different models

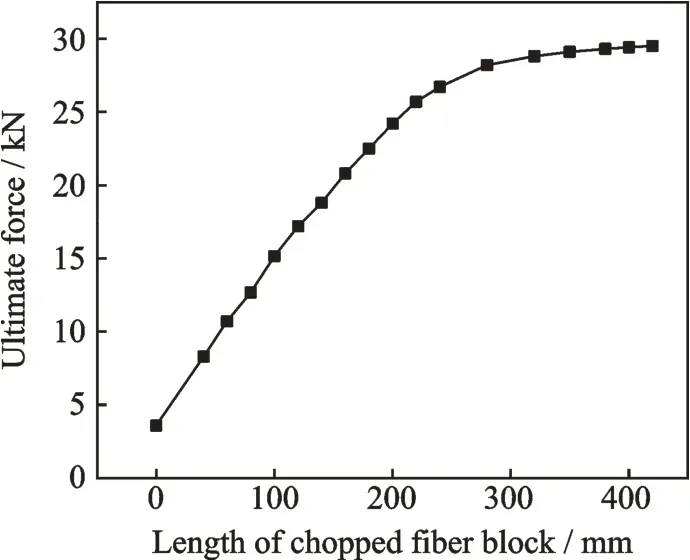
图18 极限载荷与短切纤维块长度关系曲线Fig.18 Relationship between the ulimit load and the length of chopped fiber block

通过分析发现，短切纤维块长度增加可以显著提高帽形筋结构的承载能力。对于不含短切纤维块的帽型筋结构，承载能力较弱，极限载荷仅为3.59 kN，破坏方式为筋条在加载点处发生压塌破坏；当短切纤维长度为60 mm 时，极限载荷提高至11.7 kN，结构整体刚度和承载能力均得到很大提高，极限载荷较不含短切纤维预填块模型提高了226%，同时，破坏位置也发生改变，含短切纤维预填块块的模型在筋条短切纤维与泡沫交界处“压断”。由图18 可看出，结构弯曲承载能力随着短切纤维块长度增加，呈不断增加的趋势，但增速逐渐降低。

3 结论

（1）本文建立了含预填块复合材料帽型单筋板实体模型，基于ABAQUS 软件，根据复合材料单层板Hashin、Tsai⁃Wu 失效判据，编写UMAT 子程序，结合粘聚区模型进行有限元分析。对含预填块复合材料帽型单筋板弯曲破坏形式、承载能力进行预测，得到含预填块复合材料帽型单筋板载荷⁃位移曲线、弯曲失效渐进损伤机理及相应的应力云图，同时比较了两种失效判据对计算结果的影响。其中Tsai⁃Wu 准则作为宏观失效准则，对模型的损伤预测更为保守，给出了偏安全的极限载荷，且计算量较小，工程应用上价值更高。Hashin 准则给出了具体损伤形式，便于针对损伤形式对帽型筋板结构设计和复材铺层进行改进优化，以提高承载能力。

（2）通过含预填块复合材料帽型单筋板三点弯曲试验，对有限元仿真结果进行了验证。试验结果显示：极限载荷试验值和仿真值相差比较小，破坏形式吻合较好，载荷⁃位移曲线大致一致，验证了有限元仿真分析的准确性。仿真与试验结果共同表明：共固化成型的含预填块复合材料帽型单筋板弯曲破坏形式并非筋条与蒙皮脱粘或分层，而是筋条在靠近短切纤维与泡沫交界处发生“压断”破坏。

（3）分析M1 与M2 的试验结果和仿真结果，容易发现筋条铺层层数对含预填块复合材料帽型单筋板弯曲承载能力存在较大影响，M2 比M1 多4 层铺层，极限载荷提升53.2%，提高筋条铺层层数可显著提高结构承载能力。

（4）本文根据有限元仿真对结构中短切纤维块长度进行了参数化研究，仿真结果显示：短切纤维块的存在改变了复合材料帽型单筋板弯曲破坏位置和形式，能较大的提高帽型筋结构承载能力，且随着短切纤维块长度增加，其极限载荷呈不断增加的趋势，但增速逐渐降低。实际应用中，可根据需要在帽型筋板压力集中部位填充长度合适的短切纤维预填块（即实际使用环境中连接销钉部位等有集中载荷作用的地方），避免承载点过早被压塌导致结构失效或承载能力下降。