基于峰度量化标记形态模糊度的标记分布学习
许哲源,秦 天
(南京理工大学 计算机科学与工程学院,江苏 南京 210094)
如何处理歧义性分类任务一直是机器学习中的一个热门问题。多标记学习(Multi-label learning,MLL)是一种有效的学习范式。MLL通过将传统的单标记扩展到多标记来处理模糊问题[1],使一个实例可以对应多个逻辑标记。但是MLL只能回答“哪个标记可以描述实例?”的问题,而不能回答“每个标记对这个实例的描述程度如何?”。为了更好地解决这种歧义性分类问题,Geng等提出了标记分布学习(Label distribution learning,LDL)[2]。与传统的学习范式不同,LDL的输出是概率分布形式,每个标记对应的值可以解释为该标记描述实例的程度[3],称为标记描述度。
LDL已经在多个应用领域取得成功。通过将单标记数据转换为标记分布,Geng等提出了用于面部年龄预测的标记分布解决方案[4]。这种方法通过增强一个实例来促进相邻年龄段的学习。后来LDL被用于处理面部表情识别问题[5],类似的应用还包括文本情感识别[6]和视觉图像情感分析[7]。LDL在主观评价性应用上也表现良好,例如电影评分问题[8]。LDL在医学领域也逐渐被用来解决少样本环境下的分类问题,例如基于磁共振血管造影的胎儿脑部年龄预测[9]。
文献[3]提出了标记歧义性的概念,即一个样本可以同时不同程度地对应多个标记。文献[4-6]则通过利用这种标记歧义性来提升分类学习算法,文献[10]则更进一步通过挖掘标记之间的相关性来提升预测。本文认为这种分布形态模糊度可能在LDL有着重要的作用。本文区分了标记形态模糊度与标记歧义性的异同,解释了形态模糊度的概念,给出了一种量化方法,并给出了经验发现。本文设计了一种利用形态模糊度相关策略的标记分布学习算法。试验部分设计了消融试验,以验证本文所提算法的有效性。
1 标记分布学习中的标记形态模糊度
1.1 标记形态模糊度的概念
在以前的LDL工作中,标记歧义性和标记形态模糊度的概念经常会被混淆。所以本文首先区分样本歧义和标记模糊的概念。
标记歧义性(Label ambiguity,LA)表示对一个实例存在多种合理的解释。在文献[11]中,“i.e.,label ambiguity,which refers to the uncertainty among the ground-truth labels”,即用LA来表示标记上的歧义程度。文献[3]提出了LA,但并没有给出准确定义,可以把这里的LA理解为样本歧义性,指的是对于一个实例存在多种可能的解释,可以通过添加额外的信息来消除这种歧义。样本歧义是问题的一个属性,对这种歧义问题建模是LDL的一个主要应用。从歧义性角度可以得到一种标记分布的新观点,即LDL中的每一个标记都可以看作是对一个实例的合理解释,对应的值可以看作是这种解释的合理程度。
标记形态模糊度(Morphological ambiguity,MA)表示描述一个标记分布形态的平坦程度。在本文中,标记模糊是指标记分布形态的模糊程度(缺乏清晰度或区分度)。标记模糊只与标记分布的形态有关,是标注数据的一个自然属性。
标记形态模糊度是对样本歧义性的隐式反映,它可能会受到标注不一致的影响。标注不一致有两个含义:不同的标注者可能会因为价值观和成长经历不同而对同一个样本给出不同的标注;即使是同一个标注者,也会因为心理状态的变化,在不同的时间对同一个样本给出不同的标注[12]。标注不一致现象的存在,导致对于同一样本的不同标注会有不同的形态模糊度。也就是说对于给定样本,其样本歧义性是确定而唯一的,而其标记形态模糊度却会随着标注情境的不同而发生改变。
1.2 基于峰度量化标记形态模糊度

(1)
式中:
(2)

标准化在保持矩的比例不变的同时保持分布的形状不变,从而有助于比较不同概率分布的形状[12]。四阶标准矩则被称为峰度,定义[14]为
(3)
式中:mk用式(2)计算。偏度(三阶标准矩)和峰度都是分布形态的度量方法,区别在于偏度反映分布的不对称性,而峰度反映分布的极差情况[14]。在标记形态模糊度方面,本文更倾向于一种反映分布差异性的测度,而不是不对称性。因此,本文用一个关于峰度的函数测量标记形态模糊度。峰度表示一种分布的独特程度,本文可以通过取峰度的倒数来给出模糊度的一个度量,并通过计算上限和下限将其放缩到[0,1]。
对于具有n个分量的分布,Dalén[1]证明峰度的上界为
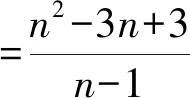
(4)
其下界为1,由Pearson不等式给出[16]。
定义1MA是指标记分布形态的模糊程度,通常反映了标记缺乏显著值,本文采用基于峰度的函数来对其进行定义和度量
(5)
式中:κ由式(3)给出,τ由式(4)给出。A的值域为[0,1]。
1.3 模糊度损失评价指标
标记形态模糊度量方法不仅适用于人工标注的数据,同样也适用于对于预测分布进行评估。本文希望分类器能够给出与真实分布较为接近的预测。当分类器给出低于真实分布的模糊预测时,便发生了预测模糊度上的损失。本文提供了一种关于模糊度损失的评估指标Laloss,它可以反映分类器在预测时相对于真实分布的形态模糊度预测损失。
定义2Laloss度量当预测比标注(真值)更模糊时发生的标记形态模糊度损失,定义为
Laloss=max(Apred-Aground,0)
(6)
式中:

(7)
Apred表示用式(5)计算得到的预测标记形态模糊度,Aground表示真实标记形态模糊度。
1.4 对学习过程的影响
在对标记形态模糊度的研究过程中,低模糊度的数据更有利于分类器的学习。本文设计了一个有两个对照组的比较试验。首先,根据模糊度将训练数据分为等量的两组,低模糊组和高模糊组。然后,对这两个对照组使用相同的算法训练两个模型,然后在相同的测试集上评估每个模型。
2 标记分布学习算法设计
2.1 符号框架
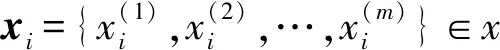
2.2 目标函数
加权距离损失让分类器先学习简单的概念,然后再逐渐学习复杂概念。由于拥有清晰标记分布的样本往往对应着易于识别的特征信息,推测分类器学习对应的样本要比学习模糊标记的样本更容易。加权距离损失的计算公式为
(8)
式中:ωi=κ(Di),可以预先计算和存储。测量两个分布之间的距离有许多不同的标准,这里使用KL散度(Kullback-Leibler divergence,KL),计算公式如下
(9)
标记模糊对齐损失:分类器期望预测的每个实例与其标记形态模糊度相匹配,它允许分类器更好地学习分布的形状,同时,还可以避免分类器为了规避惩罚而做出模糊的判断。标记模糊对齐损失项设计如下
(10)
式中:κ(d)表示分布d的峰度,用式(3)计算。
2.3 实现细节
2.3.1 预测模型
(11)

2.3.2 目标函数
相应地,参数矩阵Θ*确定如下
(12)
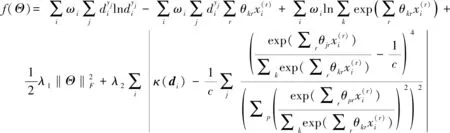
(13)
2.3.3 梯度计算
标函数f(Θ)的最小化可以由BFGS算法有效求解,式(13)的梯度如下
(14)
式中:
(15)
(16)
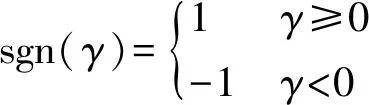
(17)
2.3.4 多阶段学习
首先学习有效的分类信息,然后优化形态模糊。在第一阶段,将模糊损失项的系数设置为0,以便分类器可以专注于分类信息。经过一定次数的迭代后,在第二阶段增加模糊度损失项,使分类器逐渐关注分布形态的模糊度损失,如表1所示。

表1 LDL-KQA算法
3 试验部分
3.1 数据集
试验中使用的LDL数据集可以根据问题的性质可以分为四类。同一算法在不同类型的数据集上的性能可能会有很大差异[18],数据集的详细信息总结在表2中。
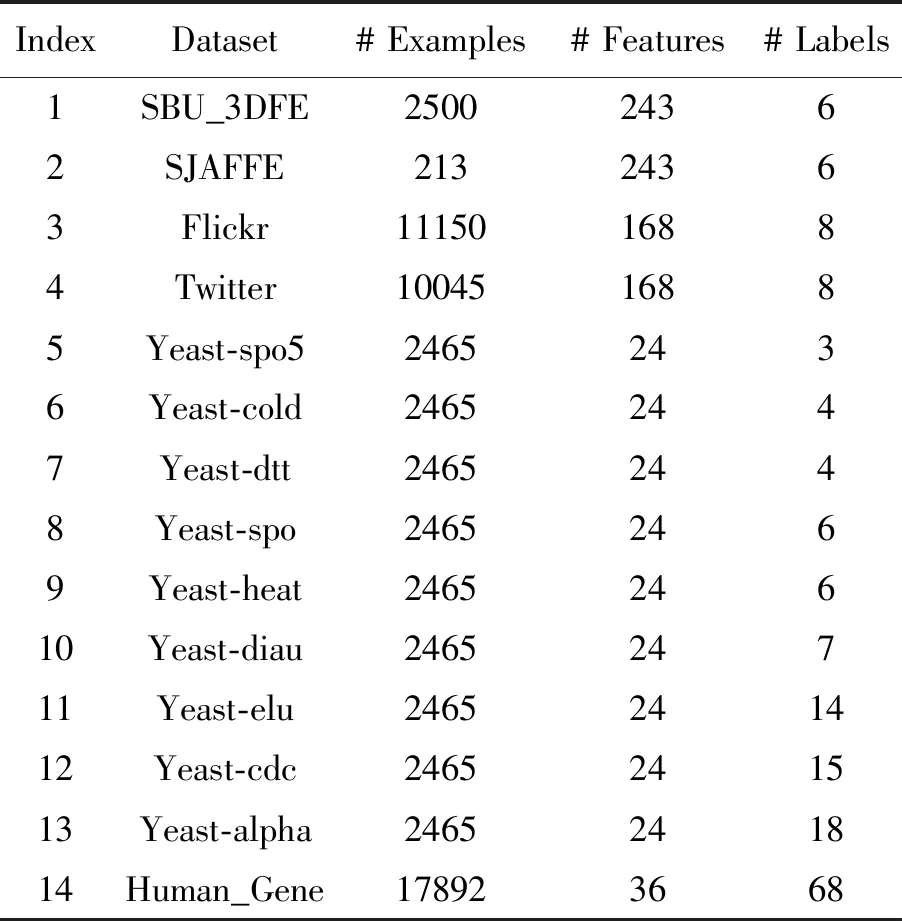
表2 试验所用14个真实数据集的基本信息
面部表情数据集:SJAFFE数据集[5]包含10个日本女模特的213张灰度图像。每张图像由60个人对6种基本情绪(即快乐、悲伤、惊讶、恐惧、愤怒和厌恶)用五个等级进行评分,其中1代表最低情绪强度,5代表最高情绪强度。用每个情绪的平均得分(归一化后)表示标记分布。第二个数据集SBU_3DFE[5]包含2 500张图像,每个图像的标记分布以与SJAFFE相同的方式获得。通过局部二值模式[19]从每幅图像中提取一个243维的特征向量。
图像情感数据集:Flickr和Twitter数据集[22]分别包含11 150和10 045张图像。它们的标记属于典型的八种情感空间(愤怒、欢喜、敬畏、满足、厌恶、兴奋、恐惧和悲伤),用三种流行的描述器(局部二值模式,方向梯度直方图和颜色矩)提取图像特征。最初提取的特征是高维的,用PCA将特征维数降低到168。
酵母菌生物数据集:酵母菌系列的九个数据集是从芽殖啤酒酵母的生物学试验中收集,共使用2 465种啤酒酵母,每个都由长度为24的相关系统发育图的向量表示[22]。标记对应于不同条件下的生物试验中的离散时间点,每个时间点的归一化基因表达水平对应于相应的标记分布。由于标记值(在相应目标元素处测量的Cy5/Cy3荧光比)来自精密仪器,因此这些标记比人工标注更一致。
人类基因数据集:人类基因数据集是从生物学研究中收集的人类基因与疾病关系的大规模真实数据集[20],该数据集包含30 542个人类基因,每个基因用一个有36个基因序列的数字描述器表示,这些标记对应于68种不同的疾病。
3.2 试验设置
3.2.1 LAG vs. HAG对照试验
为了验证本文的猜想——低模糊度数据更有利于分类任务的学习,本文设计了如下对照试验。对每个数据集,使用十折交叉验证。即将数据集随机均匀划分为10份,每次试验取其中9份作为训练集,剩下的1份作为测试集,重复进行十次试验。用Mersenne Twister算法[19]将随机数生成器的种子设置为0,确保对照试验的可重复性。首先,根据标记形态模糊度将训练数据分成数量相同的两组,将数据按照模糊度量值进行由小到大排序,并模糊度值较小的前50%划入低模糊组(Low ambiguity group,LAG),将剩下的50%划入高模糊组(High ambiguity group,HAG)。为了保持类平衡,这种划分是在按照最大分布值进行投票所获得的每个类别的内部进行的。这一过程类似于one hot编码过程,即选取每个样本对应标记分布中描述度最大的标签作为类别代表。以SJAFFE表情数据集为例,由于标注者对于“恐惧”这一情绪的识别能力较弱,对于以“恐惧”为主导的样本在标注的形态上倾向于模糊。如果不进行上述处理,那么“恐惧”为主导的样本可能全数被划分到HAG。通过预先在训练集上划分出各个情绪(例如“恐惧”)主导的类,然后再在每个类别的内部中按照形态模糊度进行排序划分成LAG和HAG两个组别。这样做可以保持各个分组中的类分布尽可能与训练集中的一致,避免某一类别被全数划分到LAG或HAG当中的某一组别,从而一定程度上保持了类平衡。然后,将LAG和HAG分别作为新的训练子集提供给相同的算法进行学习。这样,就可以分别得到关于一种算法的LAG和HAG的两个模型。最后,在同一个测试集上对两个模型进行评估。对每个算法在每个数据集划分上重复上述过程。选取不同类型的LDL算法,并试图包括每种类型[7],即问题转换(Problem transformation,PT)、算法自适应(Algorithm adaption,AA)、专用算法(Specialized algorithm,SA)。在对照试验中实现了六种LDL算法,即PT-Bayes[21]、AA-kNN[3]、SA-IIS[3]、SA-BFGS[3]、CPNN[22]和LDLLC[10]。其中PT-Bayes代表PT类算法,AA-kNN和CPNN代表AA类算法,SA-IIS、SA-BFGS和LDLLC代表SA类算法。其中CPNN是浅层的感知机网络算法,而LDLLC则是考虑了标记间相关性的SA类算法的改进。通过选择多种类型的算法进行对照试验,能够增加试验结论的可靠性。算法代码由原作者提供,根据并行性准则对这些算法进行了一些运行效率的改进。采用相应文献中报告的建议参数,所有算法的参数设置如下:对于PT-Bayes,用最大似然估计求高斯分类条件下的概率密度函数。AA-kNN中的邻居数k设置为5,CPNN的隐藏层神经元数设置为50,LDLLC中的系数设置为0.1和0.01,SA-BFGS和LDLLC的最大迭代次数设置为400。用分类任务中常用的评价指标准确率(Accuracy,Acc)来评估预测表现,“↑”表示越大越好。
3.2.2 LDL-KQA消融试验
为了验证提出的算法在降低Laloss上的表现,进行了消融试验。数据划分与对照试验相同,均采用十折交叉验证和固定随机数种子。在消融试验中,将LDL-KQA与基础模型进行比较。对于LDL-KQA,约束模型复杂度的正则项系数λ1设置为1e-5,模糊对齐项系数λ2设置为1e-3,第一和第二学习阶段的最大迭代次数设置为400。对于只加权(Weighted)的情况,λ2设置为0。对于只进行模糊对齐(Alignment)的情况,公式(8)中的权重ω设置为1。对于基础模型(Baseline),λ2设置为0,式(8)中的权重ω设置为1,其他未提及的设置保持不变。对于消融试验,同时使用Laloss和Acc来评估预测性能,Laloss的定义由式(6)给出。对于Laloss,“↓”表示越小越好,对于Acc,“↑”表示越大越好。
3.3 结果和讨论
3.3.1 LAG vs. HAG对照试验
对照试验的结果如图1所示,分别讨论不同类型的数据集。

图1 LAG模型与HAG模型的准确率差异
一类是表情和情感数据集(数据集1到4),这类数据集由人工进行标注,包含了标注不一致的情况;另一类是酵母菌数据集(数据集5到13),这类数据集由试验仪器标注,包含了标注一致的情况;此外还有一类特殊的基因数据集(数据集14),包含了高维标记的情况。计算了每种算法的LAG模型(即在LAG上训练所得的模型)和HAG模型之间的准确率差异,并将它们表示在图1中结果分为上下两行共14个簇,每个簇用于表示一个数据集的对比结果,数据集名被标注于簇的上方。每个簇由六种算法比较结果的柱状图构成,其中每个分量的值表示对应图例算法的LAG和HAG准确率的差值,即Acc(LAG)-Acc(HAG)。从结果中可以观察到,大多数算法对低模糊度数据可以达到更高的准确率,这表明标记形态模糊度低的样本更有利于分类器的学习。可以观察到SA-IIS和SA-BFGS在数据集SJAFFE上有完全不同的结果,尽管它们优化的是相同的损失函数。在文献[3]中提及了这一问题,SA-BFGS是SA-IIS算法在优化方法上的改进。这两种算法都由原作者提供,在试验中加入这两种不同优化程度的算法来模拟实际应用情景下可能出现的不同情况。SJAFFE是一个小的表情数据集,只有213个实例,具有高度的标注不一致性。一些算法(如LDLLC、SA-IIS和SA-Bayes)在这个数据集上未能拟合。准确率约为22.88%的模型无法拟合数据,并输出初始模型的预测值(用单位矩阵初始化的矩阵)。
对于表情和情感数据集(数据集1到4),LAG模型的平均准确率高于HAG模型。从图1的上半部分,可以观察到6种算法的LAG模型的性能大多优于HAG。:对于酵母菌系列数据集(数据集5到13),LAG的性能大多数情况下优于HAG。然而,在Yeast_cold和Yeast_elu数据集上,LAG的平均准确率略低于HAG。缺乏标记不一致性似乎削弱了LAG的优势。对于人类基因数据集(数据集14),标记有68维,而特征只有36维,这对分类任务来说是一个很大的挑战。可以观察到LAG模型在这个数据集上有明显的优势。在多数情况下,低形态模糊数据意味着有分明的标记。而当分类问题复杂时,部分算法例如SA-IIS由于学习能力较弱,在少量分明标记数据上无法拟合并过早退出迭代,则会导致图1中负值现象的出现。
3.3.2 LDL-KQA消融试验
消融试验的结果见表3和表4,用粗体表示更好的性能。结果表明LDL-KQA算法在Laloss和Acc指标上都优于基础模型。这说明两种策略组合对于降低预测的模糊度损失和提升分类预测准率是有效的。由于任务背景的多样性,不同的策略在不同任务中效果不一致,最优结果的分散说明了两种策略在不同问题背景下各占优势。试验结果表明,对低模糊度样本进行加权的策略更具有鲁棒性。
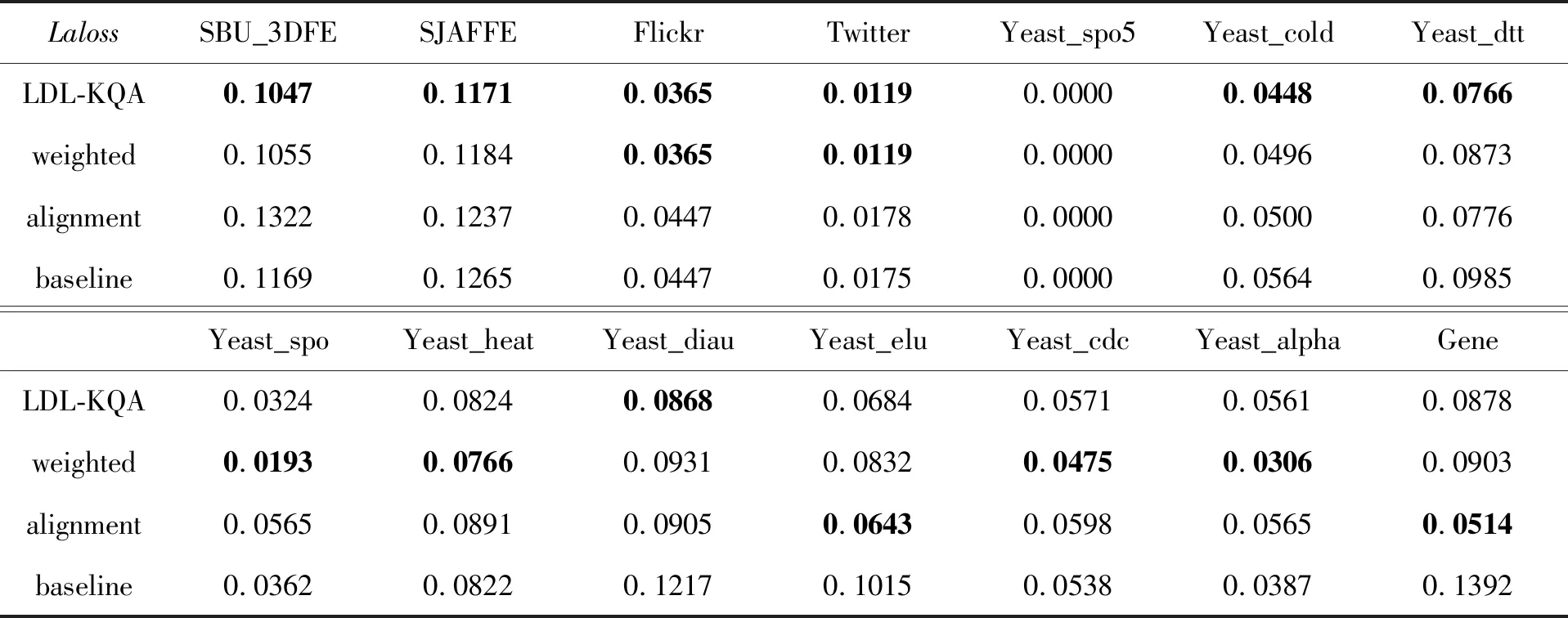
表3 LDL-KQA消融试验的Laloss↓
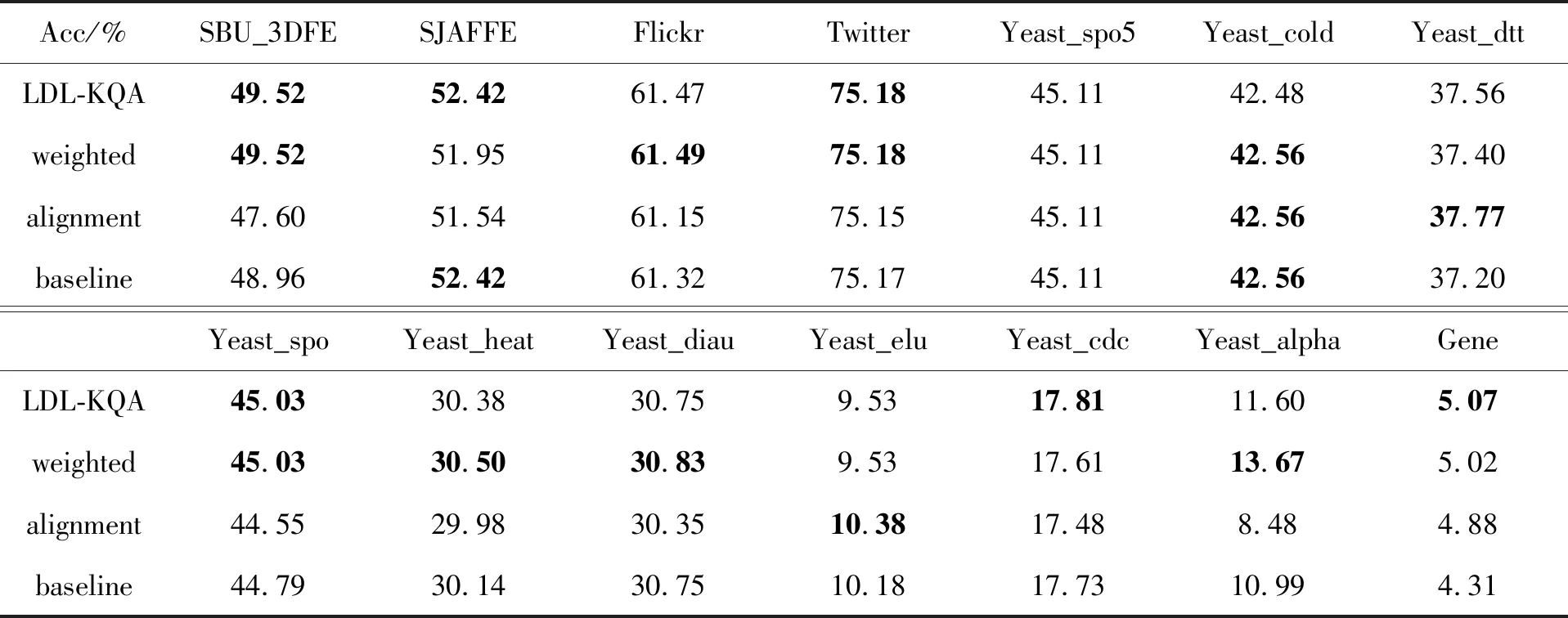
表4 LDL-KQA消融试验的Acc(%)↑
5 结束语
本文研究了LDL问题中分布形态模糊度对于学习的影响。设计了一种基于峰度的函数可以准确地度量这种分布形态上的模糊程度,从而可以对模糊程度不同的样本进行区分。发现了低模糊度的样本更有利于歧义情境下的分类学习,并据此设计了一种新的LDL算法。通过利用模糊度加权和损失对齐的策略,该算法能够利用分布中形态模糊度信息。消融试验的结果表明,本文所提出的LDL-KQA算法在各种不同类型的数据集上都有效地降低了Laloss损失,并同时有效地提高了分类准确率。本文对于分布形态模糊度的研究,在某种程度上揭示了分布形态与样本歧义性之间关系。相信这对于今后LDL相关工作会有启发,可以在现有工作的基础上进一步挖掘这种标记形态模糊度在不同场景中的作用,并针对具体情境设计基于形态模糊度的LDL解决方案。

