基于人工鱼群算法的交通信号灯配时优化模型
吴啸宇,李慧慧,林娟娟,房 新
(南京理工大学 自动化学院,江苏 南京 210094)
交叉口拥堵一直是困扰城市交通的重要难题之一。为了解决该难题,合理的信号配时是十分重要的。Webster算法作为信号方案设计中最常用的算法,虽然简单易计算,但是该算法仅适用于非饱和流量的交叉口信号优化[1],而在城市交叉口中高峰时期往往会出现过饱和现象和严重的交通拥堵问题。因此,针对这些交叉口的信号优化,则需要去研究计算机技术和智能化算法求解信号配时优化问题。
为解决上述问题,很多学者都提出了采用非线性规划模型、多目标控制模型及延误模型等来改善交叉口运行现状[2-4]。文献[2]提出一种以车辆排队长度以及交叉口延误作为优化目标的自适应交通信号控制方法,并结合物联网实现动态控制。文献[3]将多交叉口的延误指标联系起来,寻找延误最低的信号时序策略。文献[4]考虑了行人过街条件下的交叉口的车辆停车次数及交通事故因素,并根据其影响建立了双阶段信号优化模型来提高交叉口通行效率和安全性。由此可见,在交叉口优化研究中车辆延误和停车次数是相当重要的评价指标。在构建数学模型后,选取良好的求解算法同样非常重要,在交叉口问题中算法求解将更看重时效性和收敛效率。目前,求解交叉口问题的算法研究有很多,比较成熟的有遗传算法、蚁群算法、量子退火算法、禁忌搜素算法等[5-7]。但遗传算法优化过程过于复杂,在有限时间内不易找到全局最优解[5];蚁群算法同样寻优较慢,效率较低[5];量子退火算法则更适合解决局部最优问题[6];禁忌搜素算法更偏向于解决非饱和流条件下信号控制优化问题[7]。本文发现人工鱼群算法具有对参数数值要求较低且寻优能力较强的特点[8],这与具有动态性、随机性的交叉口优化问题有着较高的契合性,且目前对人工鱼群算法在交叉口问题中应用的研究较少。基于此,本文将人工鱼群算法与信号控制优化相结合,建立优化模型并针对算法的不足进行改进,以优化交叉口的通行现状。
1 交通信号灯配时优化模型
在交叉路口信号控制中,车辆延误和停车次数两个指标对交叉口通行状态具有较大影响,在本文中将以这两个参数构建过饱和交叉口函数优化模型,所用到的参数表达含义如表1所示。

表1 数学模型参数含义
1.1 优化参数的函数关系式
在目标函数方面,本文选取并分析了车辆延误和停车次数这两个主要优化目标参数。
1.1.1 平均延误的函数关系式
在平均延误方面d,计算主要通过求随机延误dr和一致性延误du之和来作为计算依据[9]。随机延误dri和一致性延误dui的计算过程如式(1)和(2)
(1)
(2)
λi=gei/C
(3)
本文所需的平均延误DI的计算可以通过不同信号相位的平均延误进行加权计算所得
di=dui+dri
(4)
(5)
1.1.2 平均停车次数的函数关系式
在平均停车次数方面为使交叉口正常通行,应尽量避免车辆二次停车,争取一个周期内车辆全放完。平均停车次数为hi的计算过程如式(6)
(6)
本文所需要的车辆平均停车次数HI的计算方式同DI,通过加权计算所得
(7)
1.2 交通信号灯配时的函数模型
在构建目标函数时,本文所期望达到的效果是,平均延误和平均停车次数最小,以达到良好的道路通行状态。由上两者的量纲不同,本文要对这两个参数进行无量纲化,在此处取β作为转换参数,将停车次数转换为时间单位。同时本文考虑到这两个参数在不同的交通条件下对实际交叉口通行能力具有不同的影响。因此引入加权系数α将这两种参数指标统一起来进行优化。α、β值取决于实际交叉口的交通状况,本文案例中α值取0.5,β值取C/2。本文基于以上描述建立了交叉口函数优化模型,其目标函数为
f(x)=F(DI,HI)
(8)
minf(x)=minF(DI,HI)=
(9)
除目标函数外,一个完整的数学模型约束条件也是必不可少的。一般情况下,n表示信号相位数时,信号周期应满足大于等于15*n,且小于等于200s的要求[9]。周期时间由绿灯时间和损失时间L两部分构成。交叉口保持良好的通行状态需饱和度xi满足0.6~0.9,同时信号配时的最小绿灯时间需满足行人过街的要求。所以有式(10)、式(11)、式(12)
15*n≤C≤200
(10)
(11)
0.6≤xi≤0.9
(12)
综上所述,本文求解信号配时最优化问题所建立的数学模型为
(13)
2 基于人工鱼群算法的优化模型求解
人工鱼群算法具有收敛效率高、初始数据和参数设置要求低、整体收敛性好等优势,主要以鱼基础生活最多的位置便是营养最丰富的地方为基本寻优原理,通常算法实现模型求解主要通过人为设置寻食的人工鱼群使其模仿鱼类基本行为来探寻最优解,其核心思想是群体中个体之间的协作和信息共享,与粒子群算法类似[10]。本文将对人工鱼群算法的函数表达进行部分说明,并结合算法不足进行部分改进,得出改进后的算法流程图。
2.1 人工鱼群算法的函数描述
人工鱼群算法执行时的主要变量有:群规模N、人工鱼视野Visual、步长Step、拥挤度因子δ、算法次数Try_number、个体状态X=(x1,x2,…,xn)、人工鱼个体i和j的距离dij=|xi-xj|等。人工鱼群算法执行的函数部分包括:人工鱼当前状态的目标浓度Y=f(x)、觅食行为Prey、聚群行为Swarm、追尾行为Follow、随机行为Move等[11]。本文中不同的信号配时方案对应的便是不同的人工鱼状态,求得的便是目标函数最小时的信号方案。
2.1.1 觅食行为Prey的函数关系式
人工鱼由状态Xi于视野内选择并转变为状态Xj;计算两者的目标值Yi、Yj,评价时若Yj优于Yi,则将Xi向Xj移动;否则进行循环寻找。若达到次数上限仍未找到,则发生随机行为
Xj=Xi+Visual*Rand
(14)
(15)
2.1.2 聚群行为Swarm的函数关系式
Xi在dij
(16)
2.1.3 追尾行为Follow的函数关系式
Xi在dij
(17)
2.1.4 随机行为Move的函数关系式
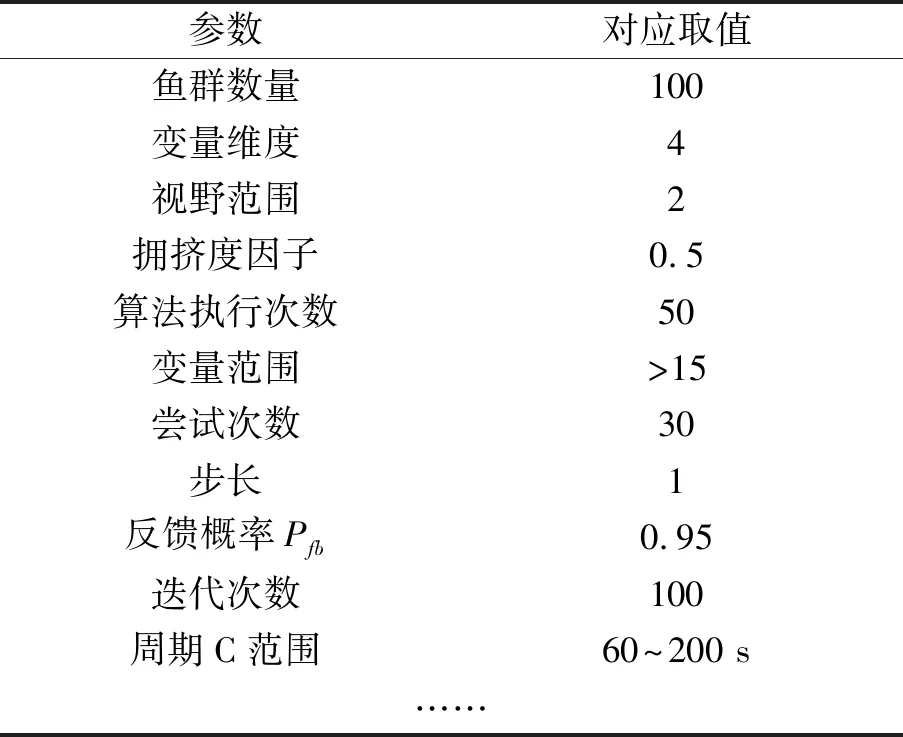
人工鱼可以在dij (18) 本文针对人工鱼群算法存在全局优化能力低、容易落入局部最佳的弊端,通过结合混沌搜索理论来提高算法全局寻优能力[11],对算法改进的实现流程如下。 步骤0假设一个优化n维变量的问题,其中第i维决策变量xi的范围为xmin,i (19) (20) (21) 由于结合混沌搜索后,提高了原算法的全局寻优能力的同时也变相的提高了算法的复杂程度,计算量大大增加。为了避免算法寻优时间过长,本文在引入混沌搜索的基础上,同时将决策论中的反馈策略[12]与本文使用的主算法进行结合。本文将反馈概率因子Pfb引入到算法的实际计算过程中。人工鱼的随机行为以概率Pfb发生,人工鱼的反馈行为以概率(1-Pfb)发生,且在整个优化过程中概率因子Pfb会随着优化的进行不断降低,用公式表示便是Pfb=γPfb,其中γ为衰减因子。通过结合反馈策略,便可以一定程度上确保在算法运行前期,人工鱼可以执行更多的随机行为,提高算法全局寻优能力;在算法运行后期,人工鱼便会执行更多的反馈行为,提高算法运行的效率。综上,得到改进后算法的执行流程见图1(a),并为了体现改进人工鱼群算法的优越性,本文以传统函数式(22)的全局极大值为例,在[-500,500]区间上进行求解,对比改进前后结果发现改进后得到的极大值837.965 8明显优于改进前的结果,且改进后算法的收敛效率得到了明显提高,具体迭代过程见图1(b)。 图1 改进后人工鱼群算法性能的验证 (22) 为使本文论证更加具有现实意义,本文将采用焦作市塔南路与工业路交叉口作为实际案例进行建模与优化。该交叉口为常规十字交叉口,在工业路东西向上为三车道设计,分别为左转、直行、直右;在塔南路南北向上为四车道设计,分别为左转、直行、直行、直右。 本文在把公交车按照规定折算为标准小汽车后,得到流量分布图。通过现场调查及数据发现高峰期出现了明显的交通拥堵的问题。详细的交叉口平峰和高峰小时流量图如图2。 图2 交叉口平高峰小时流量图 3.1.1 饱和流量计算 具体计算结果见表2,表中数据显示塔南路和工业路的车流较为稳定。 表2 交叉口饱和流量数据表 3.1.2 信号配时现状 作为配时优化所需的核心,通过调查可知该交叉口为五相位控制的交叉口,周期为155 s,右转不受信号控制。具体的交叉口信号控制状况见图3、图4。 图3 交叉口信号相位图 图4 交叉口信号配时图 3.1.3 交叉口冲突点分析 从图5中明显看出信号控制中的第4相位冲突情况比较严重。 图5 交叉口冲突点分布图 根据以上调查数据,可知该交叉口主要在高峰期间具有明显的交通拥堵问题,且高峰时交叉口饱和度很可能会大于0.9导致韦伯斯特配时法的失效。因此本文将着重从高峰时段交叉口现状入手,解决其交叉口通行问题。 3.2.1 计算流量比判断计算条件 由于右转不受信号相位控制,故不作考虑。各方向流量比为工业路(东直行:0.25、东左转:0.009、西直行:0.24、西左转:0.133)和塔南路(南直行:0.271、南左转:0.13、北直行:0.45、北左转:0.125)。由此计算总的流量比Y。 Y=0.133+0.25+0.13+0.45+0.45=1.413 (23) 从式(23)明显可知,在本例中1.413>0.9,不满足Webster算法计算条件[1],因此需要使用智能算法进行优化。从上述现状分析的交叉口冲突点图中,可以明显看出该交叉口第四相位有明显的交通冲突,因此在优化其信号配时前应先对其信号相序进行调整,结果见图6。 图6 调整后的交叉口信号相位图 3.2.2 基于人工鱼群算法的模型求解 实现方式为使用JAVA语言编写程序,主要包含算法的执行、函数的求解、公告牌的更新、人工鱼的行为描述、判断算法执行结果是否满足条件。在改进算法方面,应用混沌搜索和反馈策略,若人工鱼觅食行为尝试tryTime次后,可通过混沌算法移至下一次的位置,同时引入变量bestfish记录人工鱼的最优状态,通过比选结果对其进行更新,提高全局优化能力[13]。其中主要用到的函数模块见表3。 表3 实现算法的函数模块 在使用Java编写人工鱼群算法程序时需要设置以下参数,见表4。 表4 实现算法设置的参数变量 最终结果通过在 Eclipse软件(设备为Intel i5-5200U CPU@2.20GHz64位计算机)下求解出了该交叉口优化后的配时方案。优化后总周期为126 s,各相位绿灯时间为49 s、21 s、27 s、17 s,黄灯时间为3 s。具体结果和优化后信号相位见图7所示。 图7 优化后的交叉口信号配时图 3.2.3 使用VISSIM对交叉口进行仿真评价 分别在各进口道处设置检测器,其中检测器1~3分别测定西进口左直右车辆状况,4~6分别测定东进口左直右车辆状况,7~9分别测定北进口左直右车辆状况,10~12分别测定南进口左直右车辆状况。本文在VISSIM中分别置入优化前后的信号方案并进行仿真实验,图8显示了使用VISSIM进行仿真的主要过程。 图8 VISSIM仿真过程 仿真结束后,本文将采用多次评价并求和的方式来减少实验误差并统计实验结果。为了体现本文研究的创新性和算法优越性,在仿真部分引入传统优化方法(遗传算法优化信号配时)进行对比,其中该案例交叉口在不同配时方案下的总延误及总停车次数对比见表5。 表5 不同配时方案下的仿真结果对比表 不同配时方案下交叉口的改善情况见图9,图中主要将不同位置的平均延误和平均停车次数进行比较。其中横坐标的数字1~12对应的分别为VISSIM模型中检测器所测定的位置。 图9 不同配时方案下仿真结果对比图 从图9中可以直观地看出,本文优化方案的结果明显比原方案更优,在该配时方案下有效降低了交叉口产生的延误和停车次数,改善了路段通行现状。相较于传统优化方案而言,本文的优化方案在多处检测器测定位置下的实验结果均优于传统方案,且总延误和总停车次数也要更小,这可能是因为迭代次数50次较少导致遗传算法未找到更优的解。实验表明,使用人工鱼群算法对信号配时优化问题进行求解,具有研究的实际意义和算法优越性。 本文主要研究了交叉口信号优化问题,通过使用改进的人工鱼群算法进行求解优化模型,得到更优的信号配时方案,从而有效地减少了交叉口延误和停车次数,改善了目标交叉口的交通状况。在案例分析中,展示了本文研究方向在实际应用中的可行性,并得出了结论通过人工鱼群算法改进的信号配时方案明显优于原方案和传统优化方案,表明了人工鱼群算法改善交叉口交通状况的研究具有现实意义和优越性。在研究前景方面,未来可将人工鱼群算法不断完善使其更加适用于解决不同交通流条件下路网通行能力改善问题,实现实时调整交叉口绿灯时间,从而使得道路交通系统能便捷、高效、通畅、安全、环保的运行。2.2 人工鱼群算法的改进流程
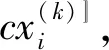





3 案例分析
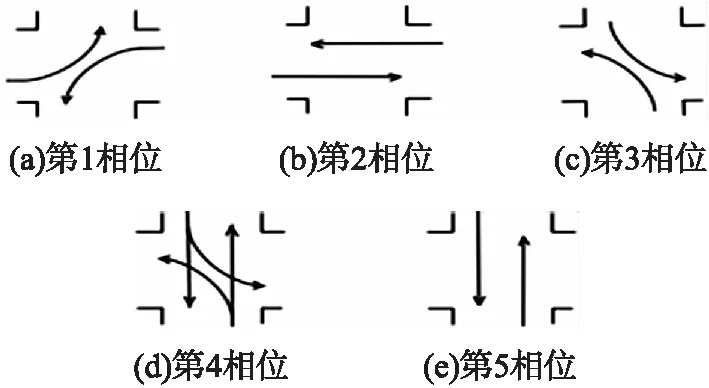
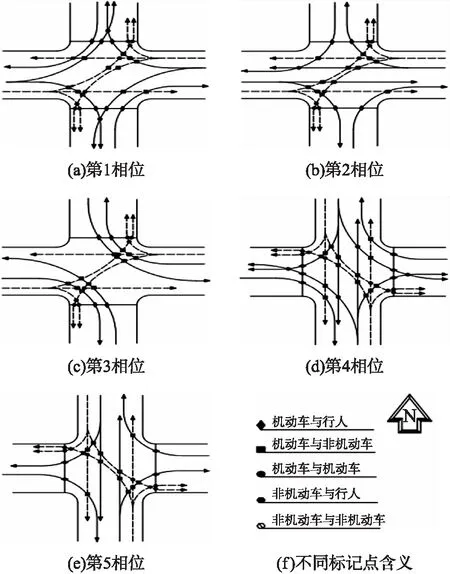
3.1 案例交叉口现状分析



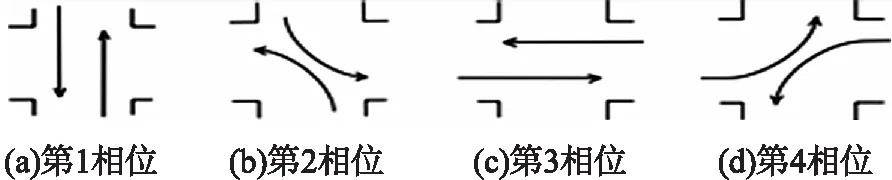
3.2 交叉口的控制优化




4 结束语

