基于近似二阶EKF 的非线性滤波仿真*
孙立珍 赵乐乐 刘广忱
(1.内蒙古建筑职业技术学院 呼和浩特 010070)(2.内蒙古工业大学 呼和浩特 010080)
1 引言
滤波问题是基于某系统的状态空间模型,通过对存在误差的实际观测量的处理,估计出系统状态量或参数的问题[1]。滤波技术先后出现有多种被用于科学研究和工程实际[2],文献[3~6]分别利用最小二乘法、极大似然法、Wiener法、粒子群算法进行滤波估计。Kalman 滤波是一种适用于线性系统的线性最小方差估计的最优递推算法,在满足其使用条件下,建立系统的状态空间模型,通过对观测量的更新来修正当前状态量的预测值,进而实现对当前状态量的估算[7]。由于工程实际涉及的系统多为非线性系统,于是应用在线性化的非线性系统滤波的扩展Kalman滤波法(EKF)被提出。
EKF 是将非线性函数的Taylor 展开式的二阶及二阶以上的高阶项忽略掉,进行一阶线性化,而线性化引起了一定的误差,特别是系统强非线性时,较大的误差可能造成滤波发散[8]。因此,在满足线性系统、高斯白噪声、所有随机变量均服从高斯(GAUSSIAN)分布的三个假设条件时,EKF 是最小方差准则下的次优滤波算法,其性能主要依赖于系统的非线性程度[9]。为了最大限度地利用系统非线性变换的前二阶矩的信息,减小由于线性化所引起的估计误差,降低滤波发散的可能性,又有人提出了近似二阶扩展卡尔曼滤波法(ASEKF)。
本文以空中抛射物为研究对象,建立抛射物的运动跟踪系统的状态方程并离散化,基于Matlab,利用ASEKF 估计系统状态量,并计算系统输出量,对物体进行跟踪,进一步了解ASEKF 的滤波原理,分析其效率,并验证其精度,也为ASEKF 的工程实际应用和Matlab仿真提供参考。
2 ASEKF的滤波原理
ASEKF 是基于线性最小方差递推滤波框架,应用状态量和观测量均值变换的二阶近似,方差和协方差进行一阶近似得到非线性系统的递推滤波框架[10]。ASEKF 可以在综合考虑估计精度和运算量的情况下,先对非线性系统方程做近似二阶非线性变换,再利用Kalman 滤波法估计系统的状态量[11]。
对于如式(1)的非线性离散系统。


ASEKF 执行流程如图1 所示。ASEKF 的滤波过程是对系统状态量不断预测和修正的过程,先对系统状态量进行预测,然后利用观测量对状态量预测值修正,获得状态量估计值,完成一个滤波过程。该方法只需要上一次状态量估计值和当前观测量来更新计算出新的状态量估计值,适用于系统状态量的实时估计。

图1 ASKEF的流程图
3 基于ASEKF的滤波仿真
3.1 空中抛射物的运动跟踪模型
假设从空中向某一方向抛射一个质量为m 的物体,其初始水平速度为vx(0),初始垂直速度为vy(0),初始位置坐标(x(0),y(0));物体运动过程中受重力mg、阻尼力、不确定的零均值白噪声干扰力的影响,且阻尼力与速度平方成正比关系,水平和垂直两个方向的阻尼系数分别为kx、ky,噪声干扰力分别为mδax、mδay[13]。在二维坐标系中,从坐标原点处观测运动物体的实时位置,距原点的距离为r,与y 轴的夹角为α,存在的零均值白噪声分别为δr、δα[14]。对某一抛射物的运动观测如图2所示。

图2 抛射物的运动观测图
根据抛射物的运动特点,选择横向位置、水平速度、纵向位置和垂直速度作为状态量,选择距离r和夹角α作为观测量,建立物体运动跟踪系统的状态方程和观测方程。由于空中抛射物所受阻尼力的方向与速度的方向相反[15],因此物体斜向上运动时的系统状态方程与斜向下运动时的状态方程不同。
1)当vy≥0、即vy是垂直向上或等于0 时,阻尼力mky垂直向下,系统离散状态方程F(X)如式(5)所示。

式(5)、(6)、(7)中,Ts为采样时间,k-1 和k 分别表示k-1时刻、k时刻。
3.2 仿真分析
根据ASEKF 的递推原理和方法,利用抛射物的运动跟踪模型可以推导出相应的滤波如式(8)所示。


式(8)包括两个部分,一是状态量、误差协方差和测量量的预测方程,二是ASEKF 滤波增益、状态量和误差协方差更新方程。该公式对状态量和测量量的预测进行二阶近似,误差协方差的预测采用一阶近似,利用测量量对状态量预测值进行修正,同时不断更新卡尔曼滤波增益和误差协方差。
在Matlab 中,基于抛射物的运动跟踪的ASEKF 滤波公式编写程序[16],主要包括真实状态量模拟、观测量构造、ASEKF 滤波和误差计算这几个模块。根据空中抛射物的运动特点和仿真需要,设定合适的状态量初值X0、误差协方差初值P0、过程噪声、观测噪声、仿真时长t 和步长Ts等参数,并运行仿真程序,抛射物的模拟真实运动轨迹、构造观测量和滤波跟踪结果如图3 所示,构造观测量误差和滤波跟踪误差如图4 所示。从仿真结果看出,构造的观测量与模拟的真实运动轨迹之间的误差较大,难以确定抛射物的真实运动状态和轨迹,而ASEKF 滤波结果与真实运动轨迹之间的误差较小,基本在2%以内,能够滤掉较大的系统噪声,较准确地实现对抛射物的运动跟踪。
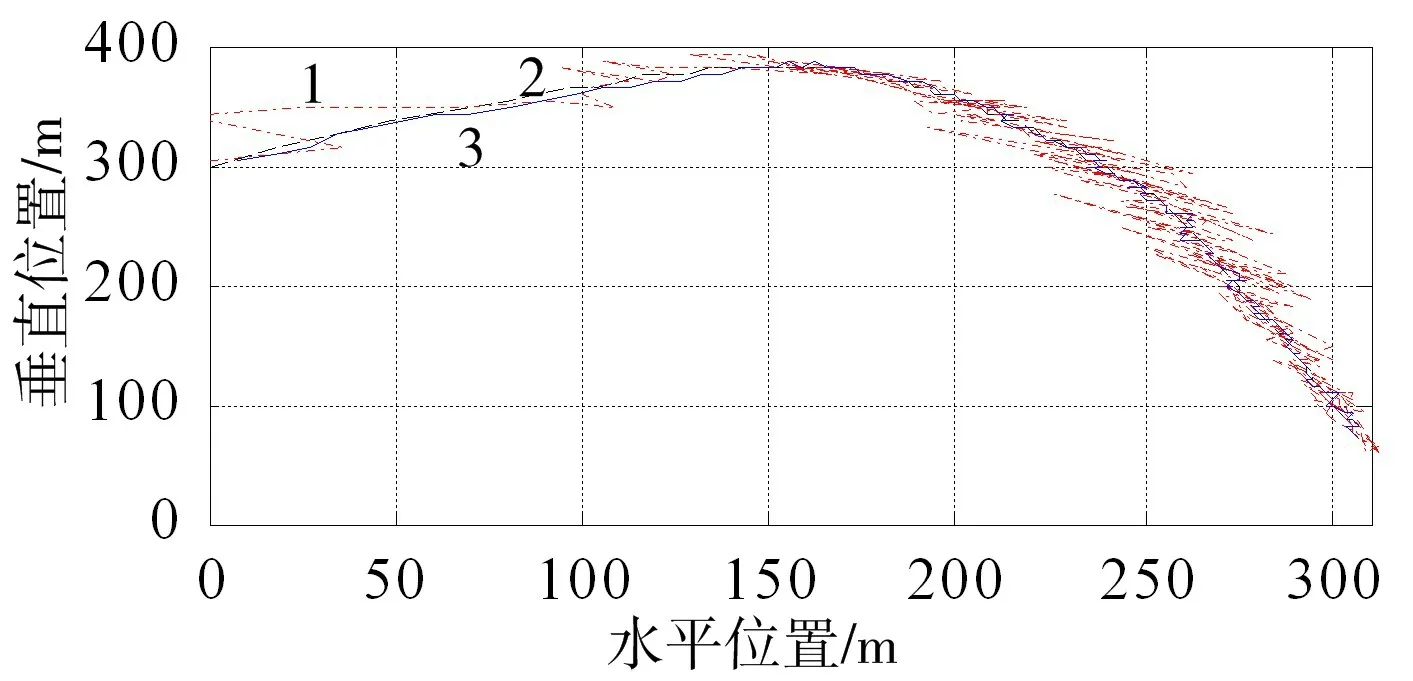
图3 抛射物的运动轨迹

图4 抛射物的运动跟踪误差
4 结语
本文首先对ASEKF 进行理论分析,了解其滤波方法和特点;然后以空中抛射物为滤波仿真研究对象,建立运动跟踪系统离散化状态方程,并根据ASEKF 的递推原理和方法推导出相应的滤波公式;最后基于抛射物的运动跟踪的滤波公式编写Matlab 程序进行仿真分析。仿真结果表明,在观测量误差较大的情况下,通过ASEKF 对抛射物的运动跟踪系统的状态量进行估计,并计算系统输出量,滤波过估计程收敛快,收敛后的误差小,只有不到2%的误差,能够较准确地实现对抛射物的运动跟踪,说明了ASEKF滤波法具有较高的估算精度。

