切换拓扑结构下多智能体系统的一致性研究*

罗俊芝 詹 环 张雪飞 闵祥娟

（陆军装甲兵学院基础部 北京 100072）

1 引言

多智能体系统（Multi-agent systems）是指由大量局部相互作用的简单个体（称为Agent）组成的复杂系统［1］。多智能体系统有广泛的应用背景，其理论运用到了车辆编队、无人机协调飞行、物流供应链系统控制等实际问题。尤其是随着科学技术的发展，多智能体系统的应用研究变得日益重要，近些年来成为控制界学者的关注的焦点［2～11］。

一致性控制问题是多智能体系统研究的重要方面，所谓一致性控制是指基于多智能体系统中个体之间有限的信息交换，设计一致性协议，使得所有智能体的某一个状态量或是所有状态量趋于相等，即使得智能体之间能够达到协调一致性，最终完成复杂任务。如Wen G H［2］针对具有无向连通拓扑结构的多智能体系统，假设每个Agent 的状态方程为连续线性模型，研究了系统的分布式一致性控制问题。Liu S［3］则针对有向拓扑结构的智能体系统，考虑了带有虚拟的Leader Agent情形，设计了含有时滞的一致性控制协议，给出了多智能体系统的一致性控制的条件。Zhang J［4］利用滑模控制对非线性多智能体系统一致性控制问题进行了研究。Li Z K 等［5］考虑了系统在有向拓扑结构下，分析了在带有界输入下的分布式一致性跟踪问题。Shen Q K 等［6］研究了固定拓扑结构下的多智能体系统的自适应一致性控制问题。

注意到文献［2～6］研究中，智能体之间采用的是固定拓扑结构，但是在实际问题中，如车辆编队控制问题，车辆的相对位置关系可能随时间的演变发生变化，从而各智能体之间的拓扑结构相应也会发生；再比如，在移动机器人进行通讯过程中，由于网络的故障造成信息传递丢失，多智能体系统的网络拓扑结构也可能发生变化，因此具有时变拓扑结构的多智能体系统的研究引起了人们的关注。目前有些文献对此问题也进行了研究，如Hu J P［7］在研究了在拓扑结构是时变的情形下，系统有Leader领导下多智能体系统的跟踪控制问题，Porfri M［8］分别针对无向定拓扑和有向定拓扑两种情形给出了保证系统几乎必然一致的充分条件，Sun Y G［9］研究了在有向拓扑结构下的多智能体系统的的一致性问题，其中系统的拓扑结分为固定有向拓扑和可变有向拓扑情形。邵俊倩等［10］研究了在变拓扑网络结构下的多无人机系统的一致性控制问题。林敏等［11］研究了时变拓扑结构下的多无人机领航跟随一致性和轨迹跟踪问题。Xue D 等［12］研究了多智能体系统在随机切换拓扑结构下的编队控制问题。

上述文献中，假定系统的拓扑结构是变化的，这种假定符合实际问题的情况，本文也考虑到实际问题中各智能体之间的拓扑结构的变化，并假设各拓扑结构的切换符合马尔可夫过程，且设计了依赖于切换拓扑的一致性协议，给出系统的一致性控制的条件。与文献［7～12］不同的是，本文给出的一致性条件与拓扑结构的邻接矩阵的特征值有关，设计了与系统切换拓扑结构切换的转移概率相关的一致性协议，并且通过理论和数值仿真可以证明在此一致性协议下推导得到的系统一致性条件，能够使多智能体的状态能够趋于一致。

2 预备知识和和系统描述

假设多智能体系统含有N个智能体，以每个智能体为节点，该系统可以抽象为包含N个节点的有向加权图G(V,ε,A) ，其中V={v1,v2,…vN}，ε⊆V×V,代表图中任意两个节点vi,vj的有向边，邻接矩阵为A=[aij]，其中aij≥0，如果aij=0,说明节点vi到vj没有边连接。如果aij=aji，则该图为无向图。L=[cij]表示邻接矩阵对应的Laplace 矩阵。

本文考虑智能体之间的拓扑结构为无向图。

假设多智能体系统的第i个Agent的动态模型为

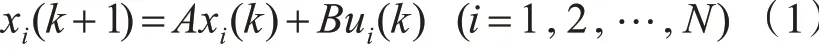
设计的一致性控制协议形式如式（2）：

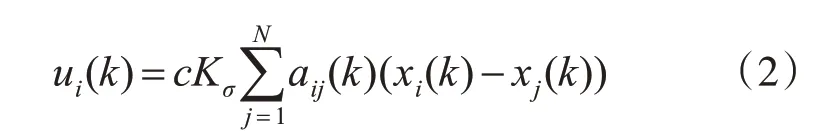
其中Kσ为控制器的增益，c为各智能体之间的耦合系数，aij(k)为邻接矩阵的元素，反映了智能体之间在时刻k时信息交互情况。

下面基于时变拓扑结构下研究多智能体系统的一致性控制问题，首先拓扑结构的变化满足如下的假设。

3 多智能体系统的一致性控制分析

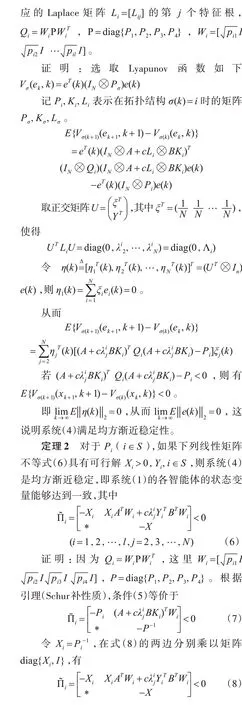
4 仿真分析

下面将针对多智能系统（1），进行数值模拟仿真，具体的系统参数取值如下：

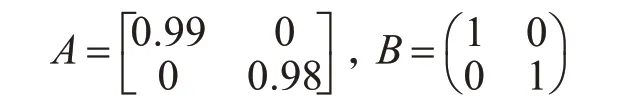
假设由6 个Agent 组成的多智能体系统，即N=6，其动态拓扑结构图在如下四种情形（图1-图4）之间进行切换，且各拓扑结构对应的转移概率矩阵为

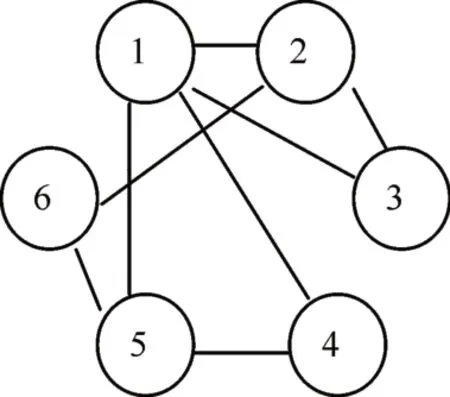
图1 拓扑结构1

图2 拓扑结构2

图3 拓扑结构3

图4 拓扑结构4

利用Matlab工具，求解条件（6），进一步求得

P1=［0.9082 0.1146；0.1146 0.9049］；P2=［0.9082 0.1146；0.1146 0.9049］；

P3=［0.9158 0.1071；0.1071 0.9123］；P4=［0.9079 0.1149；0.1149 0.9046］。K1=［-0.5042 0.6807］；K2=［-0.4989 0.6735］；K3=［-0.5039 0.6802］；K4=［-0.5022 0.6779］。

取c=0.5 ，e(0)=［1，2，1，2，3，5，3，0.2，0.3，0.6，5，4］，进行仿真得到切换信号曲线和误差系统曲线如图5和图6。

图5 多智能体系统的拓扑切换信号

图6 多智能体系统的状态曲线

结论：从仿真图形5和图形6可以看出，在系统的拓扑结构变化的情况下，通过设计与拓扑结构相关的一致性协议，多智能体误差系统的状态曲线趋于稳定，即各智能体的状态变量趋于一致，这说明了本文所提出的控制方案的有效性。

5 结语

本文针对多智能体系统，研究了系统的一致性控制问题。通过设计依赖于诸节点的时变的拓扑结构的一致性协议，且假定了该时变的拓扑结构的变化符合马尔可夫过程，利用了随机稳定性理论，给出了系统达到一致的充分条件，并给出了一致性协议的具体表达形式，借助Matlab 软件，对系统进行了仿真，验证了所提方案的有效性。