基于工业分析预测煤质发热量研究

宋宜猛

摘 要：为快速准确的预测煤质发热量，基于煤质工业分析数据，以粒子群优化算法（PSO）和支持向量机（SVM）理论为基础，采用PSO算法优化SVM超参数，建立了参数优化的PSO-SVM预测模型。在同等条件下，构建了标准SVM模型和多元线性回归（MLR）模型，并与PSO-SVM模型预测结果进行对比。结果表明，PSO-SVM模型、SVM模型和MLR模型都具有较好的预测效果，测试结果的平均绝对百分误差分别为2.433%，2.956%和3.135%;MLR模型具有较好的建模效果，但泛化性差，测试阶段出现了较大误差;参数寻优显著提高了SVM的预测精度，与线性模型相比，非线性PSO-SVM模型具有更好的泛化性和外推能力，更适合于煤质发热量的预测。关键词：工业分析;发热量;支持向量机;粒子群优化;多元线性回归中图分类号：TQ 533.2

文章编号：1672-9315（2022）01-0070-06           文献标志码：A

DOI：10.13800/j.cnki.xakjdxxb.2022.0110开放科学（资源服务）标识码（OSID）：

Research on prediction of coal calorific value

based on proximate analysis

SONG Yimeng

（Information Institute of the Ministry of Emergency Management of the PRC，Beijing 100029，China）Abstract：In order to quickly and accurately predict the calorific value of coal，

a parameter-optimized PSO-SVM prediction model is established

based on the proximate analysis data of coal，as well as on  the theory of particle swarm optimization algorithm（PSO）and support vector machine（SVM），with the PSO algorithm applied to optimize the SVM hyperparameters，and

under the same conditions，the standard SVM model and the multiple linear regression（MLR）model were constructed and compared with the prediction results of the PSO-SVM model.The research results show that PSO-SVM model，SVM model and MLR model all have good prediction effects，and the average absolute percentage errors of the test results are 2.433%，2.956% and 3.135%，respectively.The MLR model has a good modeling effect，but the generalization is poor，and with a large error occurred in the test stage.Parameter optimization significantly improves the prediction accuracy of the SVM.Compared with the linear model，the nonlinear PSO-SVM model has better generalization and stronger extrapolation ability，and is more suitable for the prediction of coal calorific value.Key words：proximate analysis;calorific value;support vector machine;particle swarm optimization;multiple linear regression

0 引 言

煤質发热量反映了单位质量煤炭完全燃烧时所能释放的能量，是衡量煤炭品质的重要指标之一，也是动力用煤计价的主要依据[1]。目前，煤的发热量主要通过弹筒量热仪测量反应物与生成物的焓差计算得到。这种方法虽然简单、准确，但实际运用中存在速度慢、工作量大等局限性。因此，为了更加快速准确获取煤质发热量，许多学者对煤质发热量预测进行了研究。LU等提出了一种将激光诱导击穿光谱技术与人工神经网络和遗传算法相结合的煤质发热量测定方法[2]。MAJUMDER等通过工业分析建立了发热量计算模型，对发热量进行了预测[3];SZER等基于工业分析和元素分析数据通过多元线性回归方法实现煤质发热量预测[4]。同时，在发热量与工业分析的非线性预测方面，周孑民等建立Elman神经网络预测模型，利用单煤的水分、灰分和挥发分含量直接预测混煤的发热量[5];WEN等基于煤质分析数据，采用小波神经网络预测煤的发热量[6];

NGUYEN等采用挥发分、水分和灰分作为关键输入变量，采用粒子群优化算法对神经网络权重/偏差进行全局搜索，研究了优化神经网络模型对煤质发热量的预测[7]。GHUGARE等基于计算智能的遗传规划形式，建立了3种基于工业和元素分析的发热量预测模型[8]。董美蓉等采用煤中某些元素（非金属元素和金属元素）的特征光谱建立了K-CV参数优化SVM的煤质发热量预测模型[9]。谭鹏、BUI等通过煤质数据分析，建立了基于支持向量回归的煤质发热量预测模型[10-11]。

虽然针对非线性关系问题神经网络具有很好的非线性逼近能力和容错性，但是神经网络方法存在收敛速度慢，易陷入局部最優及隐含层确定具有主观性等[12-13]。而支持向量机（support vector machine，SVM）在解决非线性等实际问题中克服了收敛速度慢，易陷入局部最优解等缺点，且具有精度高、泛化能力强和计算简单的特点，但SVM参数选取对其性能和预测结果有很大影响[14-15]。考虑到粒子群优化算法（particle swarm optimization，PSO）具有全局搜索优化能力强、收敛速度快且易于实现的特性，文中采用PSO对支持向量机参数进行优化选择，建立参数优化的PSO-SVM回归模型来预测煤质发热量，并在同等条件下与多元线性回归模型进行对比分析。

1 基础理论

1.1 支持向量机支持向量机[16]（support vector machine，SVM）是由Vapnik领导的研究小组于1995年首先提出的一种基于统计学习理论的VC维理论和结构风险化原理的机器学习方法，可用于模式分类和非线性回归[17-18]。支持向量机方法应用于回归问题，得到支持向量回归机（support vector regression，SVR），在支持向量机回归中，支持向量回归首先会通过一个核函数将原问题映射到高维空间，然后在这个特征空间中构造优化的线性回归函数

f（x）=w·（x）+b

（

1）式中 w为权重向量;b为偏置项;（x）为从输入空间到高维特征空间的非线性映射。

引入不敏感损失函数

L（y，f（x），ε）=|y-f（x）|=max（0，|y-f（x）|-ε）

（2）式中 f（x）为回归函数求得的预测值;y为相应的真实值;ε为不敏感损失系数。为了寻找系数ω和b，引入松弛变量ξi和ξ*i，从而得

min

w12‖w‖2+C∑ni=1（ξI+ξ*i）

s.t.

yi-w·（x）-b≤ε+ξ*i

w·（x）+b-yi≤ε+ξi

ξi，ξ*i≥0，i=1，2，…，n

（3）式中 C为惩罚因子。将式（3）的约束优化问题通过引入拉格朗日函数将其转化为对偶问题，通过求解对偶问题得到式（

1）的解[19]

f（x）=∑ni=1（αi-α*i）K（xi，x）+b

（4）式中 αi，α*i为拉格朗日乘子，αi，α*i∈[0，C];

K（xi，x）

=（xi）·（x）为核函数。

1.2 粒子群优化算法粒子群优化算法（particle swarm optimization，PSO）是由Kennedy和Eberhart于1995年提出的一种基于群体智能的优化算法。假设在一个D维的搜索空间中，由n个粒子组成的种群

W=（X1，X2，…，Xn）

，其中Xi=（xi1，xi2，…，xiD）T为第i个粒子在D维搜索空间中的位置，亦代表问题的一个潜在解。根据适应度函数可计算出每个粒子位置Xi对应的适应度值。第i个粒子的速度为

Vi=（Vi1，Vi2，…，ViD）T

，其个体极值为

Pi=（Pi1，Pi2，…，PiD）T

，种群的全局极值为

Pg=（Pg1，Pg2，…，PgD）T

。在每一次迭代过程中，粒子通过个体极值和全局极值更新自身的速度和位置，更新公式如下

Vk+1id=ωVkid

+c1r1（Pkid-Xkid）+

+c2r2（Pkgd-Xkgd）

Xk+1id=

Xkid+

Vk+1id，（i=1，2，…，n;d=1，2，…，D）

式中

ω为惯性权重，文中选择线性递减惯性权重，即ω（t）=

ωstart-

（ωstart-ωend）·

tT，其中，

ωstart为初始惯性权重，文中取值为0.9，

ωend

为迭代至最大次数时的惯性权重，文中取值为0.4，t为当前迭代次数，T为最大迭代次数;k为当前迭代次数;c1，

c2为非负常数，称为加速度因子;r1，r2为分布于[0，1]之间的随机数。为防止粒子的盲目搜索，一般将其位置和

速度限制在一定的区间[-Xmax Xmax]、

[-Vmax Vmax] 。

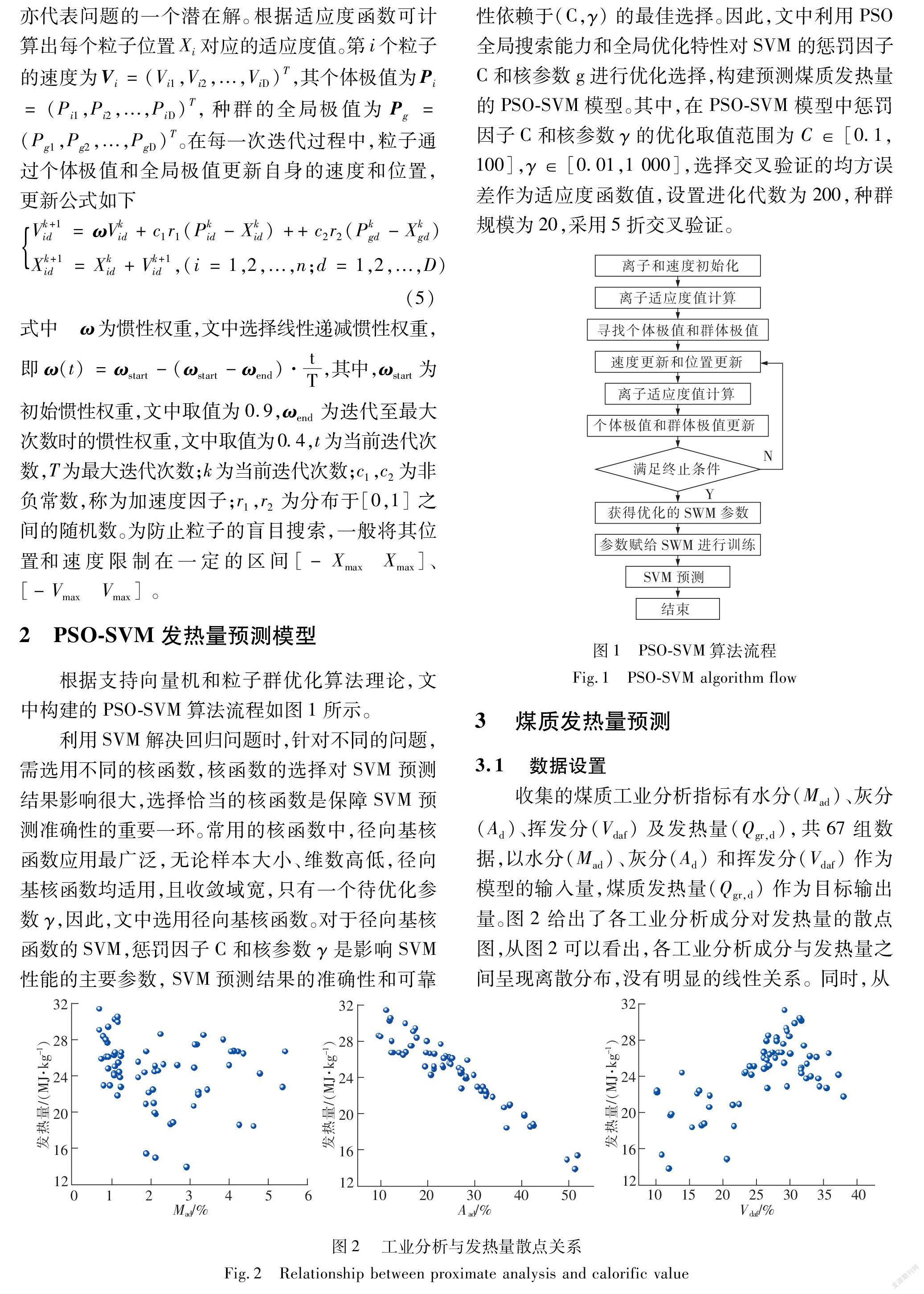
2 PSO-SVM发热量预测模型根据支持向量机和粒子群优化算法理论，文中构建的PSO-SVM算法流程如图1所示。利用SVM解决回归问题时，针对不同的问题，需选用不同的核函数，核函数的选择对SVM预测结果影响很大，选择恰当的核函数是保障SVM预测准确性的重要一环。常用的核函数中，径向基核函数应用最广泛，无论样本大小、维数高低，径向基核函数均适用，且收敛域宽，只有一个待优化参数γ，因此，文中选用径向基核函数。对于径向基核函数的SVM，惩罚因子C和核参数

γ是影响SVM性能的主要参数，SVM预测结果的准确性和可靠

性依赖于（C，

γ）的最佳选择。因此，文中利用PSO

全局搜索能力和全局优化特性对SVM的惩罚因子

C和核参数g进行优化选择，构建预测煤质发热量的PSO-SVM模型。其中，在PSO-SVM模型中惩罚因子C和核参数γ的优化取值范围为C∈[0.1，100]，γ∈[0.01，1 000]，选择交叉验证的均方误差作为适应度函数值，设置进化代数为200，种群规模为20，采用5折交叉验证。

3 煤质发热量预测

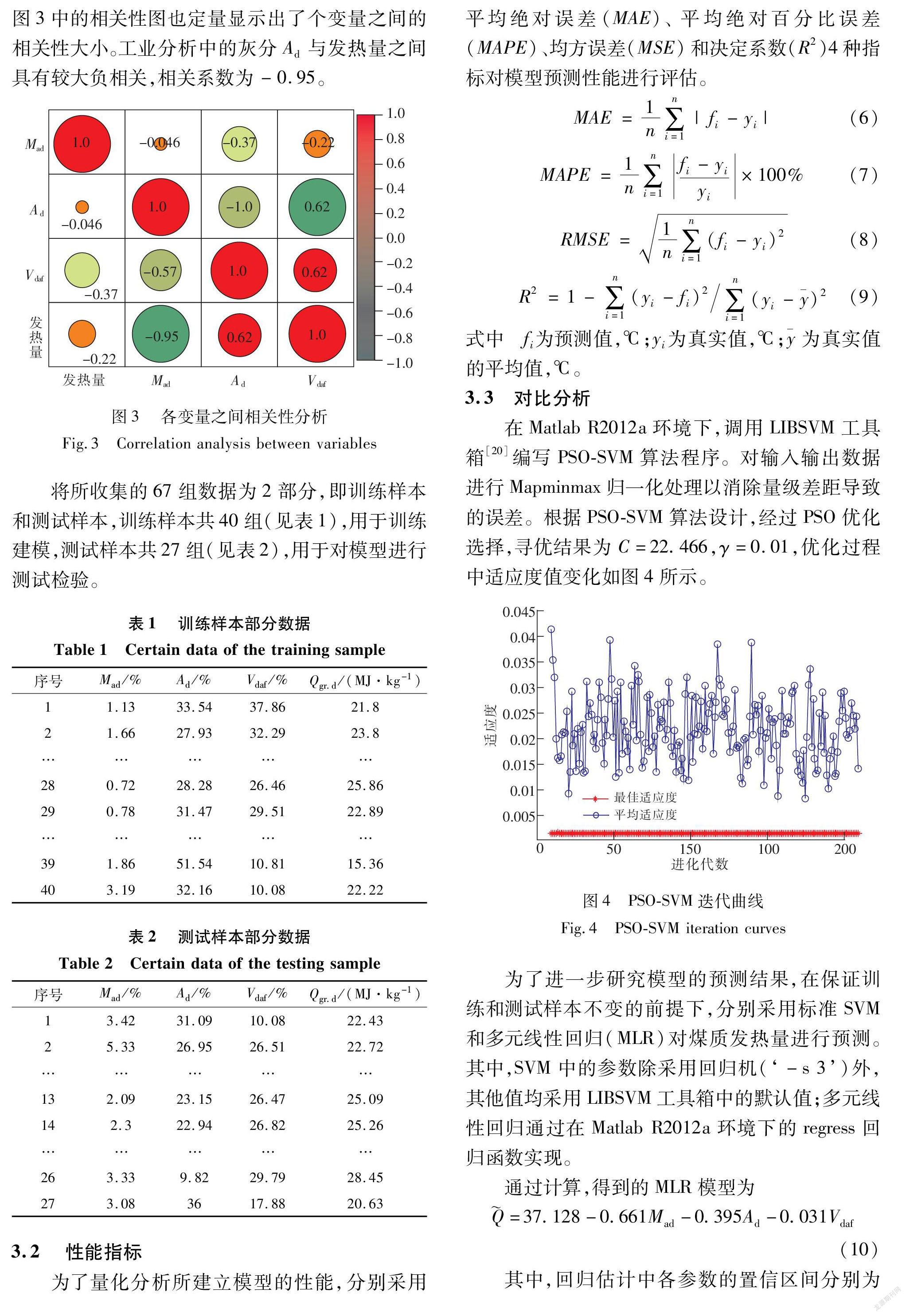
3.1 数据设置收集的煤质工业分析指标有水分（Mad）、灰分（Ad）、揮发分（Vdaf）及发热量（Qgr，d），共67组数据，以水分（Mad）、灰分（Ad）和挥发分（Vdaf）作为模型的输入量，煤质发热量（Qgr，d）作为目标输出量。图2给出了各工业分析成分对发热量的散点图，从图2可以看出，各工业分析成分与发热量之间呈现离散分布，没有明显的线性关系。同时，从图3中的相关性图也定量显示出了个变量之间的相关性大小。工业分析中的灰分Ad与发热量之间具有较大负相关，相关系数为-0.95。

将所收集的67组数据为2部分，即训练样本和测试样本，训练样本共40组（见表1），用于训练建模，测试样本共27组（见表2），用于对模型进行测试检验。

3.2 性能指标为了量化分析所建立模型的性能，分别采用平均绝对误差（MAE）、平均绝对百分比误差（MAPE）、均方误差（MSE）和决定系数（R2）4种指标对模型预测性能进行评估。

3.3 对比分析在Matlab R2012a环境下，调用LIBSVM工具箱[20]编写PSO-SVM算法程序。对输入输出数据进行Mapminmax归一化处理以消除量级差距导致的误差。根据PSO-SVM算法设计，经过PSO优化选择，寻优结果为C=22.466，γ=0.01，优化过程中适应度值变化如图4所示。

为了进一步研究模型的预测结果，在保证训练和测试样本不变的前提下，分别采用标准SVM和多元线性回归（MLR）对煤质发热量进行预测。其中，SVM中的参数除采用回归机（‘-s 3’）外，其他值均采用LIBSVM工具箱中的默认值;多元线性回归通过在Matlab R2012a环境下的regress回归函数实现。通过计算，得到的MLR模型为

=37.128-0.661Mad-0.395Ad-0.031Vdaf

（10）其中，回归估计中各参数的置信区间分别为[35.719 4，38.536 4]，[-0.898 4，-0.422 9]，[-0.417 7，-0.373 2]，[-0.063 4，0.000 8]，相关系数r2，p=0<0.05，可知回归模型成立。按照PSO-SVM模型设计与参数设置，以及MLR模型参数赋值，计算运行得到的煤质发热量的预测结果如图5所示。

从图5中可以看出，无论是训练样本还是测试样本的预测结果都分布在零误差线y=x周围，说明预测结果与真实值吻合较好，所建立的模型均能获得较好的预测结果。尤其是经过PSO参数优化之后的SVM模型，预测结果基本与真实值相一致。进一步，为了更清楚的分析不同模型的预测性能，量化各模型在训练和测试阶段预测误差和泛化性能，将PSO-SVM、SVM和多元线性回归模型预测结果进行对比，计算结果见表3。

从图5和表3中可知，3种模型的预测效果均较好，训练样本预测结果的MAE，MAPE和RMSE：MLR模型