煤岩采动应力-裂隙带发育规律研究
马建全 吴钶桥 彭昊 夏玉成 李识博 肖乐乐



摘 要:為研究煤层开采过程中上覆岩土体内采动应力-裂隙带发育规律,提出局部稳定指数的概念,定量勾绘煤层上覆岩体内破坏和未破坏的区域,并以榆树湾井田某综采工作面为例,探讨采动裂隙场及导水裂隙带发育规律。研究表明:随着工作面的推进,煤层上覆岩土体内先后产生煤层顶板破坏区、浅表层破坏区、基岩-松散层接触破坏区3个破坏区域;采动裂隙带高度随开采工作面呈现“上升—下降—上升—稳定”发育规律,而采动裂隙带宽度则呈现“线性上升”发育规律;提出裂高采比和裂宽采比的概念,得出榆树湾井田某综采工作面的裂高采比为19,基岩-松散层接触破坏区的裂宽采比为23.5,浅表层破坏区的裂宽采比为31。经对比分析,文中所提出的计算方法具有一定的验证性和适用性,可为保水采煤技术提供一定的理论依据。
关键词:局部稳定指数法;采动应力-裂隙场;导水裂隙带;莫尔-库伦强度破坏准则
中图分类号:TD 745 文献标志码:A
文章编号:1672-9315(2022)01-0107-09
DOI:10.13800/j.cnki.xakjdxxb.2022.0115开放科学(资源服务)标识码(OSID):
Development law of mining-induced stress-fracture field
in coal seam overburden
——Taking Yushuwan coal mine as an example
MA Jianquan1,2,WU Keqiao1,PENG Hao1,XIA Yucheng1,2,LI Shibo1,2,XIAO Lele1,2
(1.College of Geology and Environment,Xi’an University of Science and Technology,Xi’an 710054,China;
2.Shaanxi Provincial Key Laboratory of Geological Support for Coal Green Exploitation,Xi’an 710054,China)
Abstract:In order to study the development law of mining-induced fracture field(MFF)in coal seam overburden,a new calculation method is proposed.Taking a working face of YuShuwan coal mine as the research object,the damaged and undamaged areas in the overlying rock body of the coal seam are outlined to examine the development law of the mining-induced fracture field and the water-conducting fissure zone based on the concept of local stability index(LSI).The results show that there are three main damage areas in the overlying strata of coal seam with the advance of working face(in sequence):the failure zone of coal seam roof,the failure zone of superficial layer,the failure zone of bedrock-loose interface.In failure zone of coal seam overburden,as the working face advances,the curve trend of the height of MFF is “rising-down-rising-stable”,while the curve trend of the width of MFF is “straight rising”.The concept of the ratio of the height of MFF to mining thickness(RHM)and the ratio of the width of MSF to mining thickness(RWM)were proposed.In YuShuwan mine,RHM was 19;RWM in failure zone of bedrock-loose interface was 23.5;RWM in failure zone of superficial layer was 31.The comparative analysis shows that the calculation method proposed in this paper has verification
and applicability,providing a certain theoretical basis for water-preserving coal mining technology.
Key words:local stability index;mining-induced stress-fracture field;conducting-water fractured zone;Mohr-Coulomb failure criterion
0 引 言
煤岩采动应力-裂隙发育规律研究是生态脆弱矿区煤炭资源开采和生态环境保护中“保水采煤”研究的热点与难点之一[1-3],也是煤炭开采资源保护和矿井水灾害预测中的重点[4]。
目前对于采动裂隙带(导水裂隙带)预计高度的主要方法包括经验公式、理论分析、数值模拟、物理模拟和钻探验证等。应用最为广泛的《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规范》[5]和《矿区水文地质工程地质勘探规范》(GB 12719—9
1)[6]中推荐的经验公式;基于钱鸣高院士提出关键层理论[7]的导水裂隙带高度预计[8]等理论分析;采用有限元[9]、离散元[10-11]、有限差分[12]、RFPA[13]等数值模拟软件对导水裂隙带发育规律的分析;采用相似材料物理模拟实验方法的导水裂隙带发育高度探讨[14];运用钻孔冲洗液漏失量观测、钻孔彩色电视观测等观测法对导水裂隙带的分析[15]。综合应用这几种方法对导水裂隙带发育进行研究的,通过相似模拟试验结果、理论分析和经验公式的对比,采用回归分析法对经验公式进行修正等[16]。
随着数值模拟方法在导水裂隙带发育规律研究中的广泛应用,越来越多的学者在研究如何将开采围岩应力场与导水裂隙带发育高度相结合。王遗南基于采动前后应力场分布,提出主应力比值分析法探讨导水裂隙带预计[17];邹海等根据采厚覆岩应力的拉张区估算导水裂隙带高度[18];刘增辉等根据塑性条件、应力判别和塑性区域预测导水裂隙带[19];程香港等基于采动裂隙应力场-渗流场耦合作用下的塑性区得到导水裂隙带发育高度[20];夏玉成从构造应力角度探讨了煤矿采动损害的影响探讨[21]。
众多学者从应力角度对导水裂隙带高度进行了研究,但都是从主应力比和塑性区域估算煤层顶板破坏区的导水裂隙带高度,对基岩-松散层接触破坏区和浅表层破坏区的应力场、裂隙场探讨较少,且也未能精确勾绘出破坏区域等。OKUBO等建立了应力场与围岩破坏准则之间的关系[22],可以定量描述围岩局部稳定状态。因此,在莫尔-库伦强度破坏准则下,以简明的几何关系推导局部稳定指数计算公式,界定局部稳定指数概念,从煤层开采导致的围岩应力场变化这一角度出发,建立数值分析模型,定量地勾绘开采覆岩破坏的区域,与已有常用方法进行对比分析,以期为预测导水裂隙带发育规律研究提供一定的理论指导。
1 局部稳定指数
1.1 基本理论
局部稳定指数是指可以衡量岩土体内单个质点或局部区域稳定程度的尺度,揭露岩土体内随着应力改变而产生破坏的区域。它的大小与该点处岩土体的黏聚力c、内摩擦角φ、重度γ、弹性模量E和泊松比μ等定参量条件下所对应的应力状态(最大主应力和最小主应力)有关[23]。
在莫尔-库伦强度破坏准则下,假设岩土体内某一质点或区域所受应力如图1中实线圆所示,该点的局部稳定指数可定义为抗剪强度与其当前状态所受剪应力的比值[24],即
LSI=τfτ*
=CEBD
=CECF
(
1)
式中 LSI为局部稳定指数;τf为局部潜在抗剪强度值,kPa;τ*为局部当前状态下剪应力,kPa。
实线圆与莫尔-库伦破坏包络线的位置关系决定了该点应力状态是否稳定。若该点岩(土)体发生破坏,其极限应力状态应与破坏包络线相交于E点,E点在纵坐标上的投影代表该点潜在抗剪强度值τf;F点在纵坐标上的投影代表该点当前状态下的剪应力τ*。将实线圆向左平移至与莫尔-库伦包络线相切与点D,根据几何知识和莫尔应力圆原理,可知
在岩土体内二维空间内任意一点的局部稳定指数均可用式(5)计算求得。由图1可知当岩土体内剪应力低于莫尔-库伦破坏包络线时,局部
稳定指数LSI>1,岩土体处于稳定状态;当岩土体
内剪应力与莫尔-库伦破坏包络线相切时,局部稳定指数LSI=1,岩土体处于极限平衡状态。当岩土体内剪应力高于莫尔-库伦破坏包络线时,局部稳定指数LSI<1,岩土体处于失稳状态。因此,局部稳定指数可以定量勾绘出岩土体内不稳定的区域。
1.2 采动裂隙带计算方法
煤层开采前煤岩体处于稳定的原岩应力状态,随着开采工作面的推进,煤岩体应力状态发生改变,为了重新达到应力平衡状态,采出空间围岩会产生变形破坏向采空区内移动,围岩体内产生采动裂隙。局部稳定指数法就是在分析煤层采动
过程中岩土体内各点的应力状态基础上,按式(5)计算各点的局部稳定指数,勾绘煤层上覆岩土体内破坏区域(LSI<
1)和未破壞区域(LSI≥
1),以此来研究采动裂隙发育的方法。
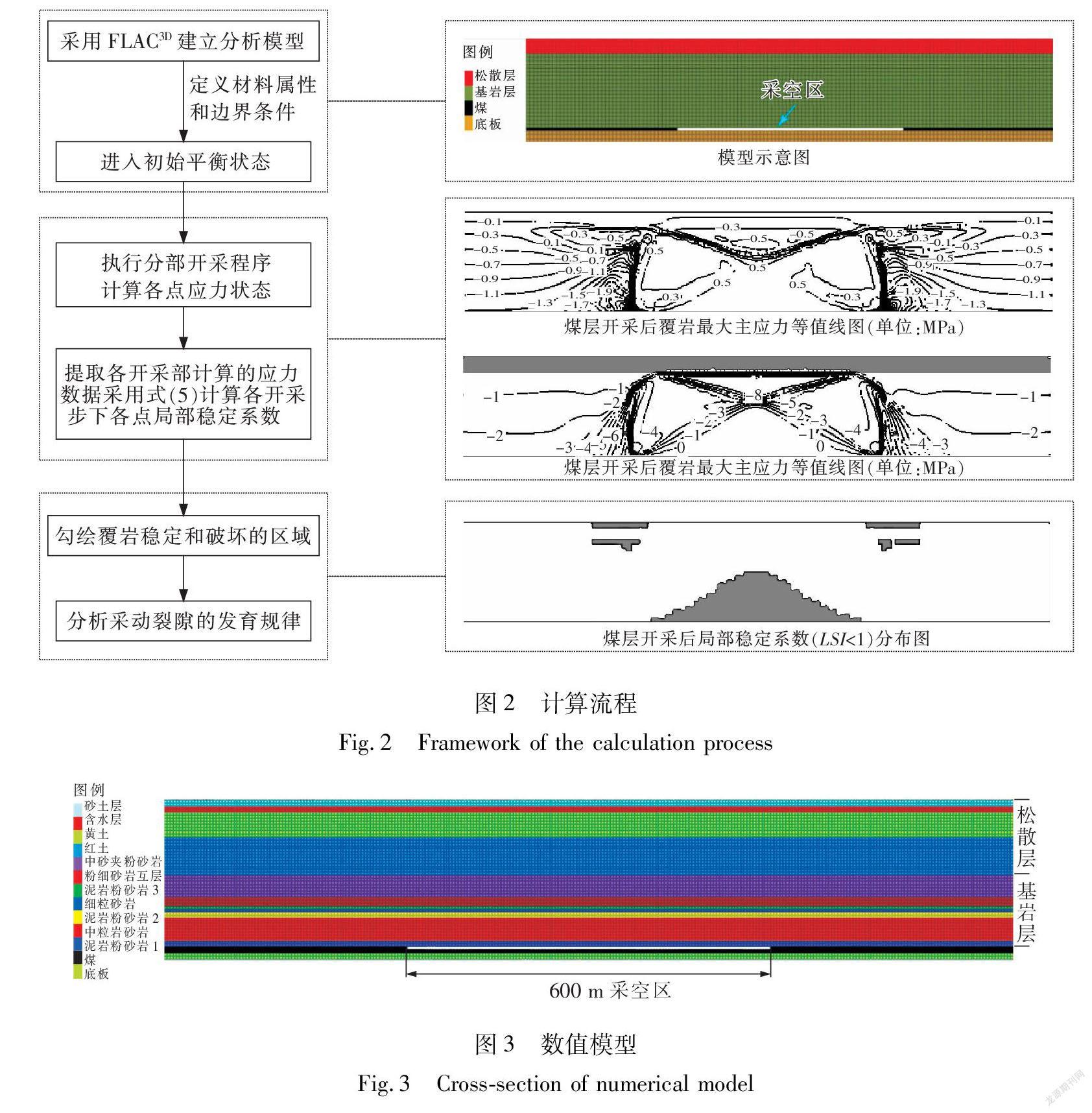
首先建立计算模型,设置煤岩土层物理力学参数(岩土层厚、弹性模量、内摩擦角、重度、泊松比和黏聚力),设定边界条件,进入初始平衡状态后,依据工作面推进实际情况,分步计算模型应力场并提取各步计算的最大主应力和最小主应力场,然后按式(5)计算各点的局部稳定指数,得到覆岩土体内局部稳定指数等值线图,对局部稳定指数小于1等值线进行填充,得到具体的覆岩破坏区域,分析评价采动裂隙带的发育规律(图2)。
2 模型建立
基于局部稳定指数计算方法,以文献[13,25]中榆树湾井田某综采工作面为例,进行采动应力-裂隙发育规律研究。工作面位于榆神矿区南部的201盘区,工作面内地层平缓,倾角0°~3°,开采2-2煤层,煤层结构简单,赋存稳定,平均厚度11.62 m,分2层开采,上分层采高5 m。井田内2-2煤层埋深110~300 m,平均埋深230 m,上覆基岩平均厚度120 m,松散层平均厚度110 m。采用综合机械化开采,全部垮落法管理顶板。井田内主要含水层为第四系上更新统萨拉乌苏组潜水含水层,隔水层是第四系中更新统离石黄土和新近系上新统三趾马红土,部分地段有上更新统马兰黄土,厚度83.75~175.0 m。
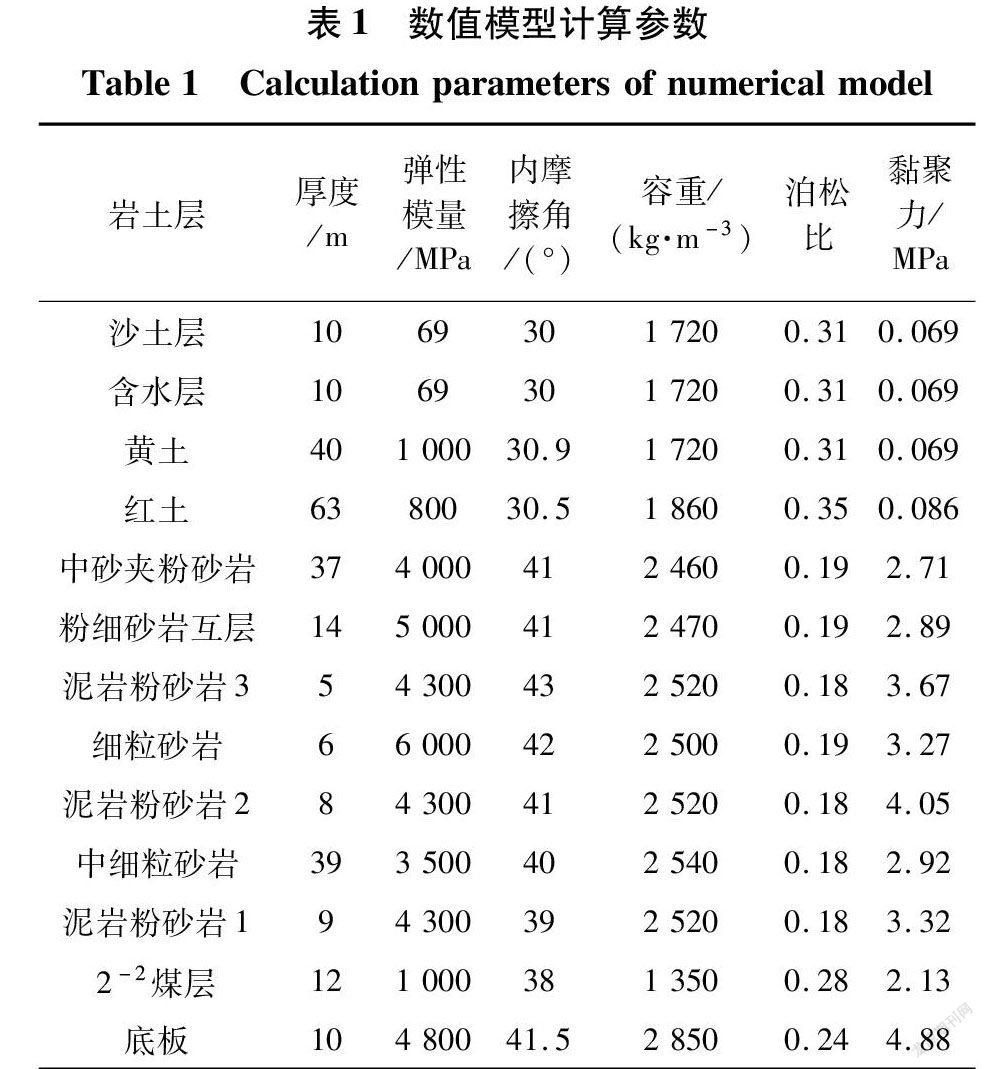
依据工作面实际地质条件和煤层赋存条件,在FLAC3D中建立数值计算模型(图3)。计算模型沿x方向1 400 m,z方向263 m,共13层煤岩层,煤层厚12 m,开采上分层,采高5 m,模型两侧施加水平约束,底部固定,顶部为自由边界。工作面总推进距离600 m,采用分步开采方式,每步开挖10 m,总共60步(表
1)。
3 计算结果
3.1 地表下沉量
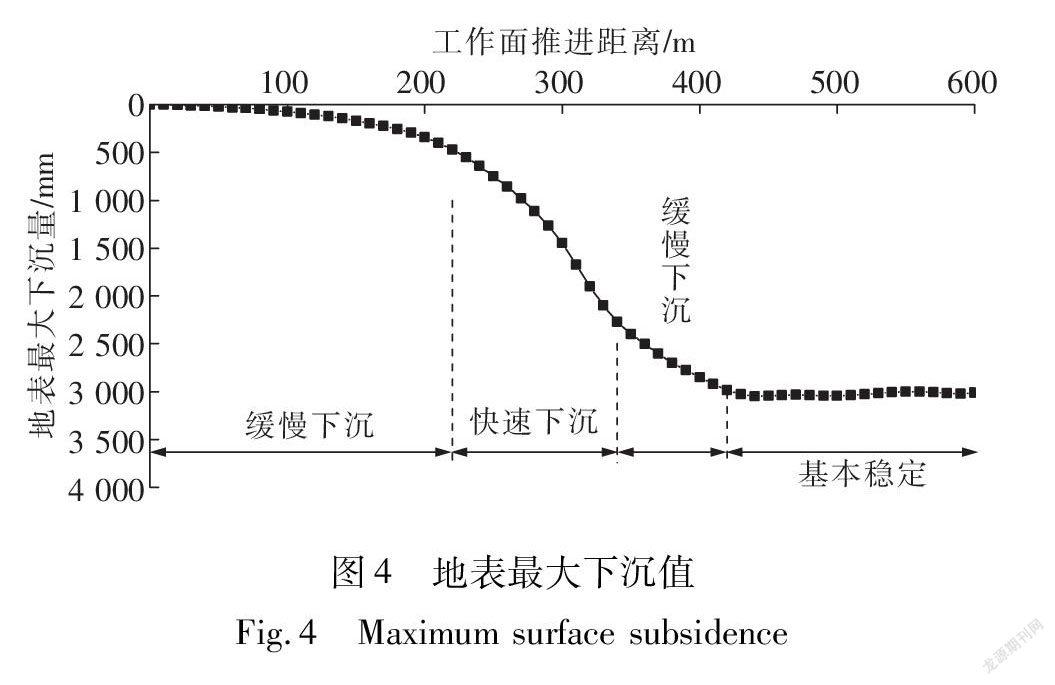
为研究地表最大下沉量随着工作面推进的变化规律,通过FLAC3D中的Fish编程,提取不同工作面推进距离时的地表最大下沉值,绘制地表最大下沉量和工作面推进距离的关系变化曲线(图4)。
由图4可知工作面推进距离在100 m以内时,开采对覆岩的扰动影响较弱,当工作面推进距离在100~220 m时,地表最大下沉值的变化曲率逐渐增大,呈现“缓慢下沉”。当工作面推进距离在220~340 m时,地表最大下沉值近乎呈直线式快速增大,呈现“快速下沉”。当工作面推进距离在340~420 m时,地表最大下沉值的上升速度明显减慢,又呈现“缓慢下沉”。当工作面继续推进时,地表最大下沉值趋于稳定,呈现
“基本稳定”。因此,地表下沉总体变化过程可以概括为“缓慢下沉-快速下沉-缓慢下沉-基本稳定”的过程。采
高5 m的地表最大下沉值基本稳定在3 020 mm左右。
3.2 局部稳定指数
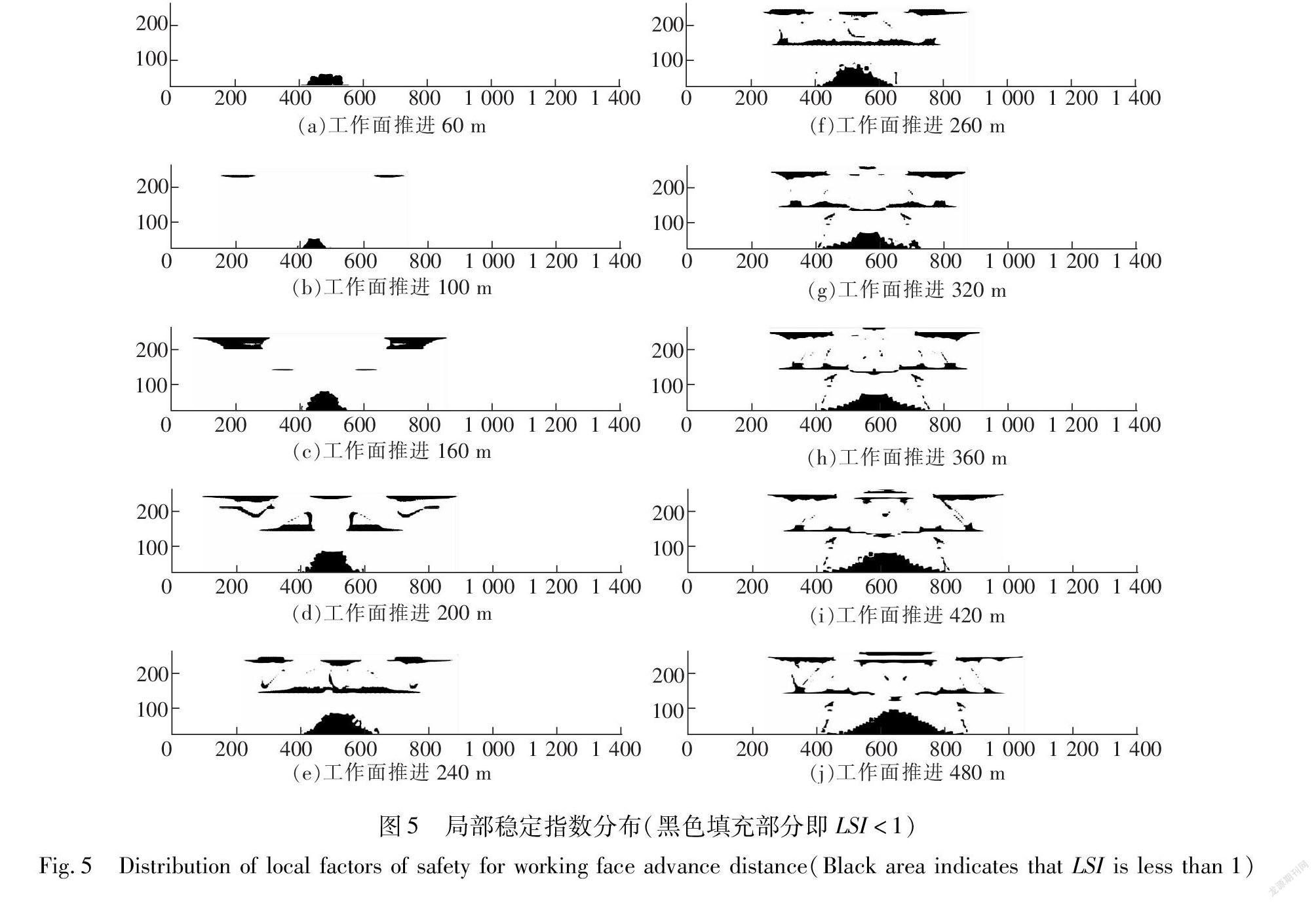
为研究覆岩破坏规律,通过FLAC3D中的Fish编程,提取不同工作面推进距离时覆岩单元的应力数据,代入式(5)计算局部稳定指数,绘制覆岩局部稳定指数小于1的分布图(图5)。
由图5可知,随着工作面的推进煤层上覆岩土体内产生3个主要的破坏区域,由下至上分别为:煤层采空区直接顶板破坏区域,称为煤层顶板破坏区(下层破坏区);基岩层与松散层红土层底部接触部位破坏区域,称为基岩-松散层接触破坏区(中层破坏区);近地表松散层破坏区域,称为浅表层破坏区(上层破坏区)。
由图5(a)~5(j)可知3个主要的破坏区域并不是同时发育的,随着工作面推进,先在煤层采空区顶板区域发生破坏,发生整体变形时,在浅表层拉张区域发生破坏。当上覆岩层距离煤层较近的岩层会发生垮落与断裂时,在基岩层与上部松散层中间会产生离层破坏区域,这一结果与朱庆伟等基于离层发展数学模型得到结果相一致[26]。因此,3个破坏区域发育先后顺序为煤层顶板破坏区、浅表层破坏区、基巖-松散层接触破坏区。
这3个破坏区域并不是独立发育,相互之间可导通。如工作面推进300 m左右时,煤层顶板破坏区和基岩-松散层接触破坏区在局部导通。
3.3 采动裂隙带发育规律
假定局部稳定指数小于1的范围为采动裂隙带发育区域,由于局部稳定指数法可定量地勾绘出采动裂隙带发育范围,因此在分析采动裂隙带发育规律时,按照采动裂隙带高度和宽度分别进行统计分析。
3.3.1 煤层顶板破坏区
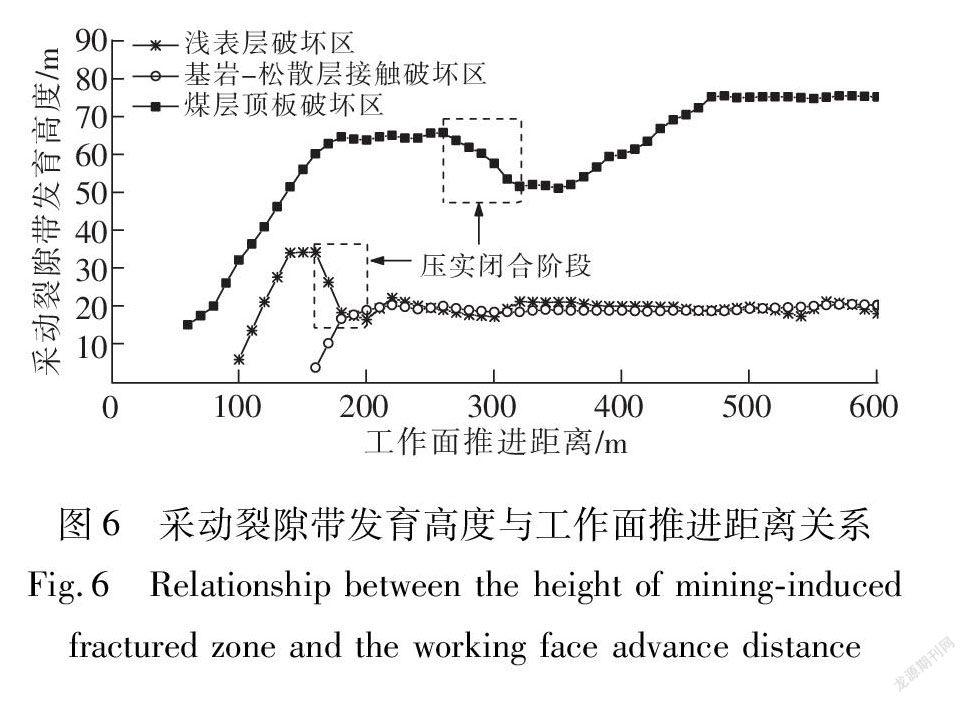
采动裂隙带发育高度:采动裂隙带发育高度为从产生到向上发展,稳定后回落再向上发展到最大高度,最终趋于稳定的过程(图6)。在工作面推进60 m后,采动裂隙带逐渐产生,发育高度为14.9 m;工作面推进到80~180 m之间,采动裂隙带高度呈直线式快速增大,由19.8 m上升至64.3 m,煤层上覆基岩破坏严重,顶板不断垮落,裂隙不断向上延伸;当工作面推进到260~350 m时,破坏的覆岩受开采扰动发生切落现象[27],部分裂隙被压实而闭合,致使采动裂隙带发育高度降低;但随着工作面推进,采动裂隙带发育高度又逐渐升高,当工作面推进到480 m后,采动裂隙高度基本达到最大值75.0 m,并稳定在该值左右。
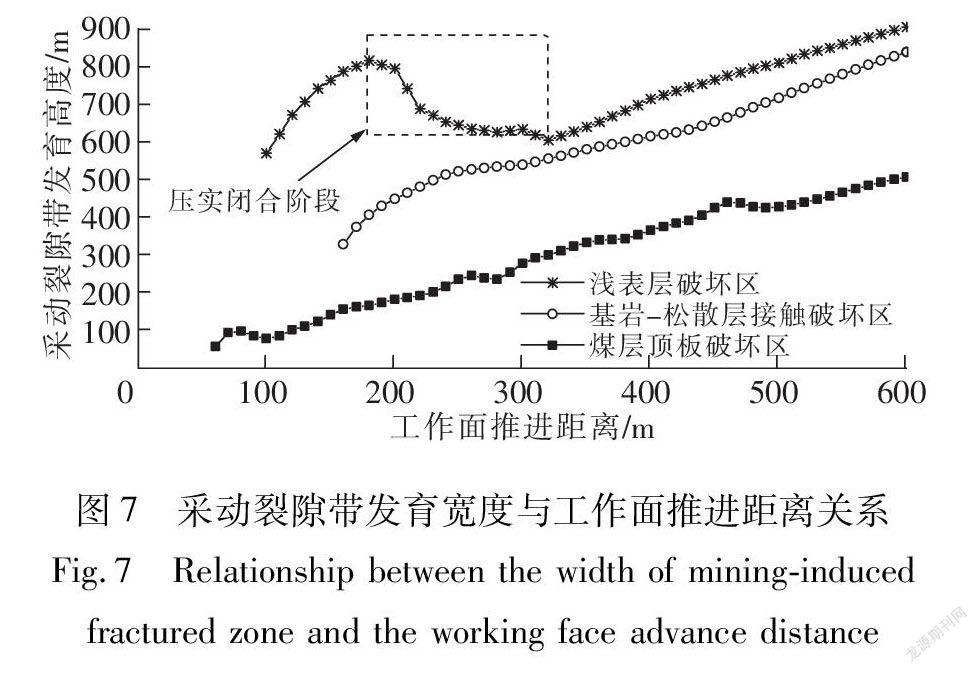
采动裂隙带发育宽度:采动裂隙带发育宽度与工作面推进距离呈线性关系,随着工作面推进距离的增加而增加(图7)。
综上所述,煤层顶板破坏区采动裂隙带高度随开采工作面呈现“上升—下降—上升—稳定”发育规律,采动裂隙带宽度则呈现“线性增大”发育规律。
3.3.2 浅表层破坏区
采动裂隙带发育高度:采动裂隙带发育高度具有一定的滞后性(图6)。在工作面推进100 m后出现,工作面推进100~160 m间,在地表移动盆地外边缘区,可能发生平行于工作面的拉张裂隙致使采动裂隙带高度直线快速向上延伸,由5.8 m上升至33.9 m;工作面推进160 m后,在地表移动盆地中心部位拉张裂隙逐渐被压实而闭合,导致采动裂隙带发育高度降低,最终随着工作面的推进稳定在19.5 m左右。
采动裂隙带发育宽度:采动裂隙带发育宽度随着工作面推进距离的增加先增加后降低再持续增加过程(图7)。在工作面推进100 m后出现,工作面推进到100~190 m间,受开采扰动影响,开切眼后方和停采线前方的近地表松散层产生裂隙,并迅速地横向延展,地表总跨度由569.7 m(破坏宽度200.1 m)上升至816.4 m(破坏宽度589.4 m);工作面推进到200~330 m间,在地表移动盆地中心部位拉张裂隙逐渐被压实而闭合,导致采动裂隙带发育宽度降低,地表总跨度由805.9 m(破坏宽度585.8 m)下降至604.1 m(破坏宽度371.5 m);随着工作面继续推进,近地表松散层内产生新的裂隙,采动裂隙带继续横向延展。
综上所述,浅表层破坏区采动裂隙带高度随开采工作面呈现“上升—下降—上升”发育规律,而采动裂隙带宽度也呈现同样的发育规律。
3.3.3 基岩-松散层接触破坏区
采动裂隙带发育高度:采动裂隙带发育高度也具有一定的滞后性,晚出现于煤层顶板破坏区和浅表层破坏区的采动裂隙带高度发育,采动裂隙带高度从产生向上发展到最大高度后基本稳定(图6)。工作面推进到160~180 m之间,采动裂隙逐渐发生并呈直线快速向上延伸,由3.8 m上升至16.5 m,之后采动裂隙发育速率明显减小,开采220 m后,上升至20.1 m左右并稳定。
采动裂隙带发育宽度:采动裂隙带发育宽度具有一定的滞后性(图7),晚出现于煤层顶板破坏区和浅表层破坏区的采动裂隙带宽度发育,但与工作面推进距离呈线性关系,随着工作面推进距离的增加而增加。
综上所述,基岩-松散层接触破坏区出现具有一定滞后性,采动裂隙带高度呈现“上升—稳定”发育规律,而采动裂隙带宽度呈现“直线上升”发育规律。
3.4 裂采比
“裂采比”的概念在众多导水裂隙带研究文献中均有论述,一般为“导水裂隙带高度与煤层开采厚度之比”。从采动裂隙带高度发育规律中发现导水裂隙带高度一般为煤层顶板破坏区采动裂隙带高度,当煤层顶板破坏区采动裂隙带高度与基岩-松散层接触破坏区采动裂隙带高度导通后,导水裂隙带高度为其两者之和。采动裂隙带宽度的发育规律也揭示了采动引起的裂隙水平发育范围也具有一定的规律。
3.4.1 裂高采比
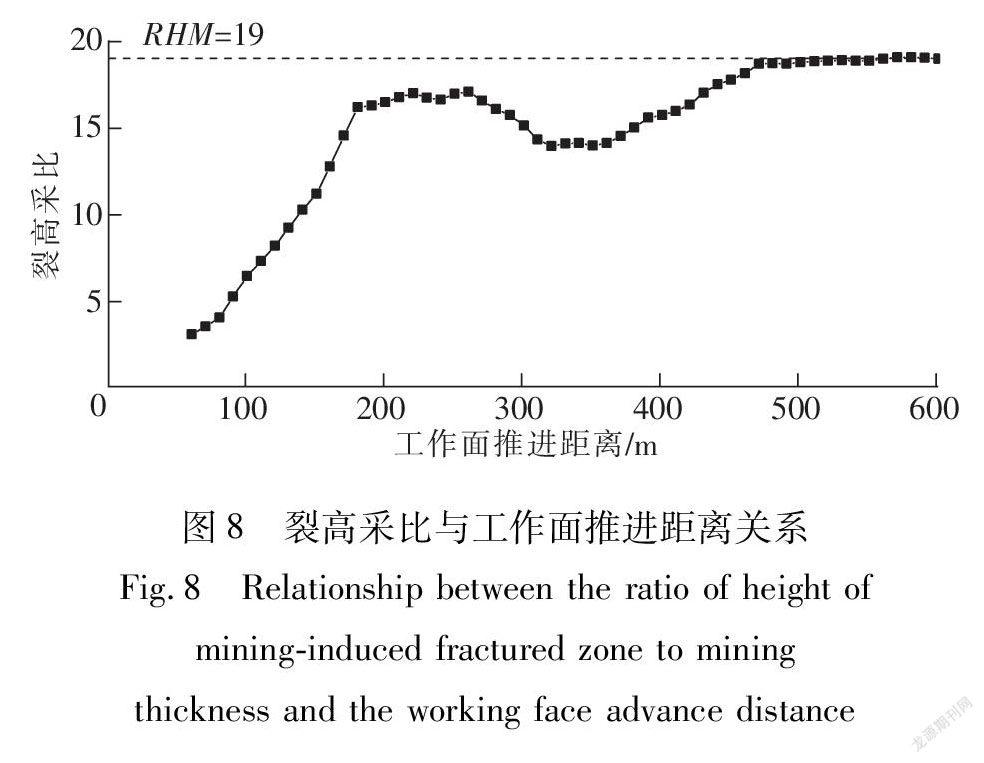
由导水裂隙带发育高度和煤层开采厚度5 m,得到了裂高采比RHM与工作面推进距离的关系(图8)。
由图8可知裂高采比与工作面推进距离并不是呈线性关系,工作面推进距离180 m之前,裂高采比呈线性增加;工作面推进距离在180~470 m间,裂高采比曲线下降后又上升;工作面推进距离470 m之后,裂高采比基本稳定在19左右。
与其他裂高采比计算方法进行对比(表2),局部稳定指数法计算得到的裂高采比比《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规范》的经验公式值要大,比RFPA和FLAC数值模拟软件的预计结果要小,与钻孔实测值较接近。与文献[28]中榆树湾物理模拟结果(裂采比为18)对比,文中计算稍微偏高,计算结果是基本可信的。
3.4.2 裂宽采比
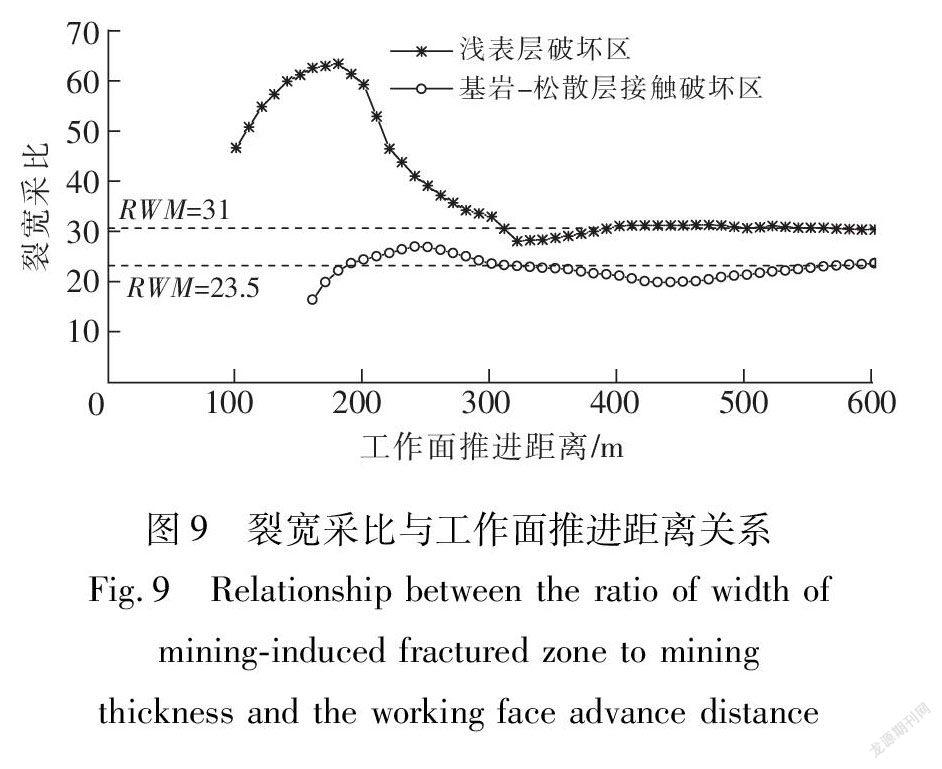
由前文采动裂隙带发育宽度可知煤层顶板破坏区导水裂隙带宽度与工作面推进距离相一致。基于浅表层破坏区和基岩-松散层接触破坏区的采动裂隙带总宽度(总跨度)和工作面推进距离,即(采动裂隙带发育总宽度(跨度)-工作面推进距离)/(2×煤层开采厚度),就得到了裂宽采比RWM(图9)。
由图9可知基岩-松散层接触破坏区的裂宽采比随着工作面推进距离变化范围较小,裂宽采比在23.5左右。浅表层破坏区的裂宽采比随着工作面推进距离变化范围较大,工作面推进到180 m,裂宽采比由47上升至63.5,此后裂宽采比下降到31左右并稳定。
4 结 论
1)局部稳定指数法可定量及动态地勾绘煤层覆岩随开采工作面推进距离的破坏和未破坏区域分布区,以此来探讨采动裂隙发育规律。
2)基于局部稳定指数法,以榆树湾井田某综采工作面为例,得到了煤层上覆岩土体随着工作面的推进,先后出现煤层顶板破坏区、浅表层破坏区、基岩-松散层接触破坏区3个主要的破坏区域,且3个破坏区域并不是独立发育,相互之间可形成连通通道。
3)依据3个破坏区域的采动裂隙带高度和宽度发育规律统计分析,提出裂高采比和裂宽采比的概念,并与其他方法进行对比,与钻孔实测值较为接近。
4)实践证明局部稳定指数法对采动裂隙带发育规律研究较符合煤矿实际情况,可为煤炭开采资源保护和矿井水灾害预测,为保水采煤技术提供一定的理论依据。
参考文献(References):
[1] 范立民.保水采煤面临的科学问题[J].煤炭学报,2019,44(3):667-674.
FAN Limin.Some scientific issues in water-preserved coal mining[J].Journal of China Coal Society,2019,44(3):667-674.
[2]王雙明,范立民,黄庆享,等.榆神矿区煤水地质条件及保水开采[J].西安科技大学学报,2010,30(1):1-6.
WANG Shuangming,FAN Limin,HUANG Qingxiang,et al.Coal water geological conditions and water conserving mining for Yushen coal mine area[J].Journal of Xi’an University of Science and Technology,2010,30(1):1-6.
[3]范立民,马德雄,等.保水采煤的理论与实践[M].北京:科学出版社,2019.
[4]张建民,张凯,曹志国,等.基于采动-爆裂模型的导水裂隙带高度计算方法[J].煤炭学报,2017,42(6):1557-1564.
ZHANG Jianmin,ZHANG Kai,CAO Zhiguo,et al.Mining-bursting simulation and height calculation method for conducting-water fractured zone[J].Journal of China Coal Society,2017,42(6):1557-1564.
[5]国家安全监管总局,国家煤矿安监局,国家能源局,等.建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规范[S].北京:煤炭工业出版社,2017.
[6]国家技术监督局.矿区水文地质工程地质勘探规范[S].北京:中国标准出版社,1991.
[7]钱鸣高,缪协兴,许家林.岩层控制中的关键层理论研究[J].煤炭学报,1996,21(3):2-7.
QIAN Minggao,MOU Xiexing,XU Jialin.Theoretical study of key stratum in ground control[J].Journal of China Coal Society,1996,21(3):2-7.
[8]许家林,朱卫兵,王晓振.基于关键层位置的导水裂隙带高度预计方法[J].煤炭学报,2012,37(5):762-769.
XU Jialin,ZHU Weibing,WANG Xiaozhen.New method to predict the height of fractured water-conducting zone by location of key strata[J].Journal of China Coal Society,2012,37(5):762-769.
[9]高明涛,辛恒奇,郭忠平,等.黄河北煤田薄煤层采场上覆岩层纵向分带发育规律[J].西安科技大学学报,2019,39(5):790-801.
GAO Mingtao XIN Hengqi GUO Zhongping,et al.Vertical zonation development of overlying strata in thin coal seam stop in Huanghebei coal field[J].Journal of Xi’an University of Science and Technology,2019,39(5):790-801.
[10]马雄德,王苏健,蒋泽泉,等.神南矿区采煤导水裂隙带高度预测[J].西安科技大学学报,2016,36(5):664-668.
MA Xiongde,WANG Sujian,JIANG Zequan,et al.Prediction on the height of water-flowing fractured zone in southern Shenmu mine[J].Journal of Xi’an University of Science and Technology,2016,36(5):664-668.
[11]吕文宏.覆岩顶板导水裂隙带发育高度模拟与实测[J].西安科技大学学报,2014,34(3):309-313.
LV Wenhong.Measure and simulation for development height of water conducted crack zone in overburden roof[J].Journal of Xi’an University of Science and Technology,2014,34(3):309-313.
[12]栾元重,李静涛,班训海,等.近距煤层开采覆岩导水裂隙带高度观测研究[J].采矿与安全工程学报,2010,27(1):139-142.
LUAN Yuanzhong,LI Jingtao,BAN Xunhai,et al.Observational research on the height of water flowing fractured zone in repeated mining of short-distance coal seams[J].Journal of Mining & Safe ty Engineering,2010,27(1):139-142.
[13]王悦,夏玉成,杜荣军.陕北某井田保水采煤最大采高探討[J].采矿与安全工程学报,2014,31(4):558-563,568.
WANG Yue,XIA Yucheng,DU Rongjun.Discussion on maximum mining height of coal mining under water-containing condition in one mine field of northern Shaanxi province[J].Journal of Mining & Safety Engineering,2014,31(4):558-563,568.
[14]孙学阳,李鹏强,寇规规,等.特厚煤层导水裂隙带发育高度的模拟实验[J].煤炭技术,2018,37(6):143-144.
SUN Xueyang,LI Pengqiang,KOU Guigui,et al.Simulation experiment on development height of water fractured zone in extra thick coal seam[J].Coal Technology,2018,37(6):143-144.
[15]王振荣,赵立钦,康健,等.多煤层重复采动导水裂隙带高度观测技术研究[J].煤炭工程,2018,50(12):82-85.
WANG Zhenrong,ZHAO Liqin,KANG Jian,et al.Technological study on height observation of water flowing fractured zone caused by repeated mining in multiple coal seam[J].Coal Engineering,2018,50(12):82-85.
[16]伍永平,于水,高喜才,等.综放工作面导水裂隙带高度研究[J].煤炭工程,2012,44(10):59-61.
WU Yongping,YU Shui,GAO Xicai,et al.Study on height of sater flow fracture zone in fully mechanized caving face[J].Coal Engineering,2012,44(10):59-61.
[17]王遗南.预计导水裂隙带的应力分析方法[J].煤炭学报,1982,7(1):92-99.
WANG Yinan.Prediction of the height of water conducting fissured zone by analyzing the stress distribution in overlying strata[J].Journal of China Coal Society,1982,7(1):92-99.
[18]邹海,桂和荣,王桂梁,等.综放开采导水裂隙带高度预测方法[J].煤田地质与勘探,1998,26(6):44-47.
ZOU Hai,GUI Herong,WANG Guiliang,et al.Forcast about the height of water fractured zone under sub-level caving method[J].Coal Geology & Exploration,1998,26(6):44-47.
[19]刘增辉,杨本水.利用数值模拟方法确定导水裂隙带发育高度[J].矿业安全与环保,2006,33(5):16-19.
LIU Zenghui,YANG Benshui.Determining height of water-flowing fractured zone with numerical simulation method[J].Mining Safety & Environmental Protection,2006,33(5):16-19.
[20]程香港,喬伟,李路,等.煤层覆岩采动裂隙应力-渗流耦合模型及涌水量预测[J].煤炭学报,2020,45(8):2890-2900.
CHENG Xianggang,QIAO Wei,LI Lu,et al.Model of mining-induced fracture stress-seepage coupling in coal seam overburden and prediction of mine inflow[J].Journal of China Coal Society,2020,45(8):2890-2900.
[21]夏玉成.构造应力对煤矿区采动损害的影响探讨[J].西安科技学院学报,2004,24(
1):72-74,78.
XIA Yucheng.Influence of tectonic stress on mining-induced ground damage in coal mining are[J].Journal of Xi’an University of Science and Technology,2004,24(
1):72-74,78.
[22]OKUBO S,FUKUI K,Nishimatsu Y.Local safety factor applicable to wide range of failure criteria[J].Rock Mechanics and Rock Engineering,1997,30(4):223-227.
[23]马建全,王念秦,张新社.基于点稳定系数法的斜坡稳定性分析[J].吉林大学学报(地球科学版),2015,45(2):533-540.
MA Jianquan,WANG Nianqin,ZHANG Xinshe.Analysis on slope stability based on local factor of safety[J].Journal of Jilin University(Earth Science Edition),2015,45(2):533-540.
[24]LU N,
BASAK S K,ALEXANDRA
W,et al.Analysis of rainfall-induced slope instability using a field of local factor of safety[J].Water Resources Research,2012,48(9):W9524.
[25]夏玉成,代革联.生态潜水流场的采煤扰动与优化调控[M].北京:科学出版社,2015.
[26]朱庆伟,李航,杨小虎,等.采动覆岩结构演化特征及对地表沉陷的影响分析[J].煤炭学报,2019,44(S1):9-17.
ZHU Qingwei,LI Hang,YANG Xiaohu,et al.Influence analysis of between subsidence and structure evolution in overburden rock under mining[J].Journal of China Coal Society,2019,44(S1):9-17.
[27]贾后省,马念杰,赵希栋.浅埋薄基岩采煤工作面上覆岩层纵向贯通裂隙“张开—闭合”规律[J].煤炭学报,2015,40(12):2787-2793.
JIA Housheng,MA Nianjie,ZHAO Xidong.“Open-close” law of longitudinal transfixion cracks in shallow buried coal face with thin bedrock[J].Journal of China Coal Society,2015,40(12):2787-2793.
[28]黄庆享.浅埋煤层保水开采岩层控制研究[J].煤炭学报,2017,42(1):50-55.
Huang Qingxiang.Research on roof control of water conservation mining in shallow seam[J].Journal of China Coal Society,2017,42(1):50-55.
1275501186371

