结构化教学:让复习课堂充满生长力
施娅林
“结构”一词在文学艺术等创作中颇为常见,茅盾在《漫谈文艺创作》一文中说道:“结构指全篇的架子。既然是架子,总得前、后、上、下都是匀称的,平衡的,而且是有机性的。”只有精心构思,巧妙建构,艺术作品才能成为匀称、和谐、统一的有机整体。教学也是一门艺术,复习课是整体性、结构性极强的重要课型。然而,在以往的复习课教学实践中,教师往往只关注知识练习或点状突破等,忽视了教学的整体性和联结性。长此以往,碎片化的知识堆积会带来认知的无序叠加,学生无法形成整体的、有条理的认知结构。透过结构,学生更容易把握本质,快速提取信息,从而快速思考问题和解决问题。在“双减”背景下,教师要让学生减少枯燥的刷题,让复习课助力学生思维的生长。笔者从结构化的视野和低年级学生的思维特点出发,尝试对苏教版小学低年级数学复习课进行实践与思考。
一、巧设活动,拓宽思维的广度
心理学家皮亚杰认为:“思维从动作开始,切断了活动与思维的联系,思维就不能发展。”以具体形象思维为主的低年级学生尤其是这样。数学活动对于低年级学生而言,就是让学生边活动边思考,引导儿童在活动中学会全面理解事物之间的联系。因此,教师应根据低年级学生的思维特点,结合教学内容巧设教学活动,通过活动把抽象的知识具体化、形象化、结构化。这种方式不仅可以帮助学生理解数学知识,而且有利于拓宽学生思维的广度。
(一)梳理活动,整体感知
如果说课时内容是一个点,那么复习课的内容就是一条线,整个知识领域内容就是一个面。在复习时,教师应先引导学生梳理内容,帮助学生从联系的视角了解知识之间的关系,将每课时点状知识聚成线,并引导学生运用知识迁移,以点带面,帮助学生整体感知知识框架。
苏教版数学一年级上册“10以内的加法复习”是整个单元的复习课,该单元安排在“认识10以内的数”单元之后,学生初步认识了数的组成并体验了数的有序思想,并且该单元的知识对后续学习“认识11~20各数”以及“20以内进位加法”至关重要。在教学时,笔者先请学生按照自己的想法将无序的10以内的数排序,感受数的有序性以及排序方法的多样性;接着请学生找到用0~10里的数组成的加法算式;最后选择了几个学生写得很乱的算式展示给大家。全班学生看到异口同声地说:“太乱了!”笔者再因势引导:“怎样才能把10以内的加法算式一个不漏地全部说完整呢?”有了对数的排序的认识,学生很容易回答出:“有规律的整理!”
通过“给无序的数排队”的活动,学生在大脑中勾勒出了有序排列的框架,并找准“数”与“式”的关联点,将新知识对接已有知识经验,在顺应的知识链中经历知识的发生过程,突破对知识的点状理解,形成整体性认知,拓宽思维的广度。
(二)操作活动,体悟结构
教育家苏霍姆林斯基指出:“儿童的智慧在他的手指头上。”基于低年级学生具体形象思维的特点,教师将抽象的知识具体化、形象化,学生才能真正体悟结构。如何将教材中静态的知识结构转化为动态的探索对象,引导学生积极参与教学过程?这就需要教师在教學设计时,遵循数学知识的内在逻辑,通过设计操作活动,帮助学生逐步建立清晰的知识结构,获得知识的方法结构,拓宽思维的广度。
例如,在教学苏教版数学一年级上册“10以内的加法的复习”中,学生说出10以内的加法算式后,教师请学生通过小组合作的方式选择喜欢的排序方式,整理所有10以内的加法算式卡片。教师采用小组合作的方式整理,学生经历有序整理算式的过程,为知识的结构铺设框架。在动态整理的过程中,学生可以通过不同的规律来形成加法表,从头脑中的框架到直观呈现加法表的整理过程,最后形成整体的结构。学生进一步感受相关加法算式的内在联系,丰富和加深了对加法运算特点和规律的认识。
又如,在教学苏教版数学一年级上册“100以内的加法和减法的复习”时,笔者请学生分类整理所有100以内的加法和减法算式。这一活动要求学生分类整理算式,将100以内的加法算式分为进位和不进位加法算式,减法算式分为退位和不退位减法算式,由此让学生对100以内的加法和减法形成整体的认识。
教学以学生自身活动体验为主,既强调“学”与“用”,又强调“感”与“悟”,前者对学生的抽象思维能力提出一定要求,后者从贴近低年级学生的认知特点出发,根据具体事物展开抽象思考。教师对感知经验加以提炼和抽象,为学生的认知结构化铺设框架,通过探究发现蕴含在活动中的问题的属性、关系和规律,潜移默化地提高学生的思维能力。
二、寻找联系,拓宽思维的深度
小学低年级学生的思维活动在很大程度上与眼前的具体事物或其生动的表象联系着,他们所掌握的知识大部分是具体的,是可以直接感知的,要求他们从知识中指出最本质的东西是很困难的。但是,这并不是说学生的思维就没有任何的抽象性,他们没有任何的概括能力。事实上,小学低年级学生的思维同时具有具体形象的成分和抽象概括的成分,它们之间的关系随着不同性质的智力活动而发展变化着。因此,教师除了要为学生创设活动外,还需要引导学生对不同的方法进行分析、比较,从中寻找联系,突破重点,捕捉本质,提炼出基本的数学思想方法,使学生的认识不断走向深入,拓宽其思维深度。
(一)异中求同,于相同处探本源
就单个材料而言,学生很难获得规律性的认识,探寻事物的本源。通过比较,学生能够去伪存真、求同存异,关注知识本源,与数学本源进行沟通,在联系沟通中发展迁移。例如,在教学苏教版数学一年级上册“10以内的加法复习”时,笔者组织学生将各小组整理好的表格展示在黑板上,相同的展示在侧边的小黑板上。学生非常兴奋地将整理好的表格与黑板上已有的表格对比并选择合适的位置。
学生比较黑板上展示的不同加法表,生成了互补资源。通过互补资源的对比学习,学生逐步加深对10以内的加法表结构的理解和感悟,不断加深对知识之间联系的理解,实现了有意义的自主建构。学生探寻知识的本源,体会了隐藏的数学思想,实现了思维质的飞跃,拓宽了思维的深度。
(二)同中求异,于不同处求本质
教师在学生展示不同方法的基础上,引导其分析,寻找联系,能够促使学生由表及里地思考,感受数学思想方法的魅力,把握知识的本质,拓宽思维的深度。
例如,在教学苏教版数学一年级上册“10以内的加法复习”时,笔者先选择一份表格引导学生仔细观察,大部分学生横着看、竖着看之后会发现规律;接着引导学生找到斜着看的规律;最后,再选择另一张加法表,引导学生通过刚才的观察经验,学会独立横、竖、斜着看去观察表格。又如,在教学苏教版数学二年级上册“表内乘法复习”中,筆者也同样引导学生仔细观察(横、竖)乘法表。
教师引导学生在同一张表格里找到不同的规律,接着在不同形式的多张表格中寻找相似的规律。这样不仅多角度夯实基础知识,更加强了数学思想方法间的沟通,厘清了知识间的纵横联系,有利于学生整体地思考问题,把握问题的本质。通过寻找联系,学生的具体思维逐步过渡到抽象思维,在对知识进行分类、梳理、综合的过程中拓宽了思维的深度。
三、变式演绎,提升思维的高度
数学是严密的,小学生由于身心尚处在发展之中,思维水平还不能达到数学严密性所要求的高度。在数学学习过程中,在学生不甚严密的数学思维中,也存在严密性的一些主要特征,如直觉感官、注重外在形式、认同合情推理和多维度的思维方式。变式演绎是指教师选取某一数学内容,从不同角度运用不同方式对知识进行变通,从而使学生更全面、更深入地理解数学知识的内涵。因此,教师在进行复习课教学时应注重复习题的层次性,深入掌握数学知识点之间的联系,并对不同层次的题型进行变式设计,从而帮助学生串联起不同的知识点,引导他们在复习时能够自主建构网络化的数学知识结构,提升思维的高度。
(一)一题多解,纵横融通
对于一个问题,教师应从多种角度引导学生进行理解和掌握,使学生的思维进入一个求异的状态,然后在问题间建立联系,将知识的内涵和外延把握得更精准些,让学生在变式训练中拓展思维。
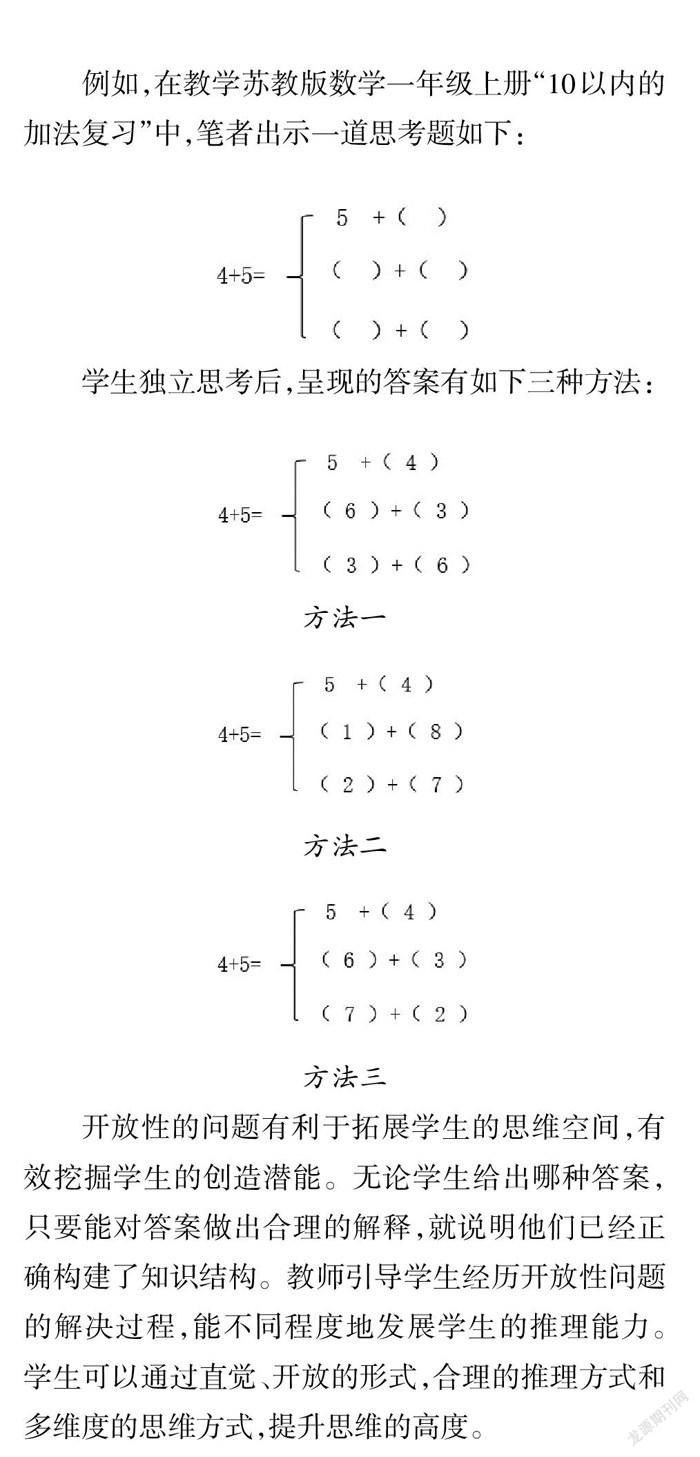
例如,在教学苏教版数学一年级上册“10以内的加法复习”中,笔者出示一道思考题如下:
学生独立思考后,呈现的答案有如下三种方法:
方法一
方法二
方法三
开放性的问题有利于拓展学生的思维空间,有效挖掘学生的创造潜能。无论学生给出哪种答案,只要能对答案做出合理的解释,就说明他们已经正确构建了知识结构。教师引导学生经历开放性问题的解决过程,能不同程度地发展学生的推理能力。学生可以通过直觉、开放的形式,合理的推理方式和多维度的思维方式,提升思维的高度。
(二)一题多变,思维进阶
在数学学习过程中,变式思考有助于打破思维定式,重组学生的认知结构,学生的思考随着问题的变化逐步深入。
例如,在教学苏教版数学一年级上册“10以内的减法复习”中,笔者请学生观察10以内的减法表,接着出示20以内的进位加法算式表、20以内的退位减法算式表和九九乘法表等以后要学习的各类表格,请学生思考,让学生从不同的角度观察这些表格。笔者从数学知识的整体出发,将本节课所学的知识渗透到以后的学习中,帮助学生边学边延展。学生得到的不应该只是数学的块状知识,还应该有数学思维的形成和学习能力的提升。
一题多变就是适合低年级学生的思维方式,将知识之间的联系通过变式呈现,进行整体结构化设计,提升学生思维的高度。
布鲁纳曾说:“获得的知识,如果没有完满的结构把它联在一起,那是一种多半会被遗忘的知识。一串不连贯的论据在记忆中仅有短促得可怜的寿命。”因此,复习课的教学犹如艺术创作,复习是学生“再生长”的过程。我们要环顾四周,站在更高处,从“有机”结构的视角设计整体性、联结性教学,助力学生的思维生长。
(作者单位:南京外国语学校河西初级中学第一附属小学)
投稿邮箱:405956706@qq.com

