基于纹理合成优化算法的多相非均质材料二维微观结构表征与重建*

解曦宇，马志远，林 莉

（大连理工大学无损检测研究所，大连 116085）

MCR 可定量表示微观结构及其固有随机性，并建立统计等效的微观结构样本[1]，从而建立正向和反向PSP 关系，来分析已知结构的材料性能或根据所需要的属性设计材料结构及加工方法，已成为材料科学前沿研究领域的热点之一[2-4]。常见的MCR 方法有随机场[5]、纹理合成[6]、相关函数[7]、物理描述符[8]等。在针对多相非均质材料的MCR 研究中，随机场重建结果的各相占比可控，但是其宏观结构与实际样本形貌存在差异，相关函数重建的计算成本大，物理描述符难以准确识别多相材料中各相颗粒的几何特征，目前均应用不多。

纹理合成起源于计算机图形学，广泛应用于遮挡填充、图像修复等领域，由于该方法具有计算成本小，重建结果更接近样本真实形貌的特点，近年来逐渐被应用到MCR 中，目前已成功应用于多相、各向异性、动态材料系统重建。Sundararaghavan[9]最先将纹理合成算法应用于单相与双相材料的MCR，针对银钨复合材料与多晶微观结构，使用沿x、y和z平面获得的3 个正交二维截面图像重建了对应的微观结构，该研究证明了纹理合成重建微观结构的可行性，但其算法优化不完善，计算效率低。Liu 等[10]在此基础上将纹理合成算法应用于三相材料，研究结果证明了其用于重建多相非均质复杂结构的可行性，但仅保证了重建结果中结构的相似性，没有对材料中各相占比进行调控。

为了对MCR 重建效果进行评估，通常需要评价所建模型的统计等效性。相关函数作为验证图像统计性质的表征方法，已广泛用于MCR 重建结果有效性的验证中。常采用的有两点相关函数[11]、两点聚类相关函数[12]、线性相关函数[13]等。其中，两点相关函数具有信息丰富、计算简便的特点，应用较为广泛。本研究以具有多相非均质特性的AlSi-PHB 封严涂层作为样本，采用纹理合成算法对其进行二维微观结构表征与重建，并以颗粒数量与各相面积分数为参数进行算法优化，通过计算重建结果的两点相关函数方差对算法优化有效性及重建效果进行评价。

1 原理

1.1 纹理合成

应用于MCR 的纹理合成算法通常假定样本服从马尔可夫随机场纹理模型，这意味着样本中任意一点像素值的条件概率分布仅与其相邻像素值相关，而与样本的其余部分无关，因此可将材料的金相照片视为纹理并保留其结构性和随机性。纹理合成通过穷尽搜索来重建图像，通过按特定顺序逐像素（或体素）重建，搜索到原始图像中的邻域匹配性最佳的像素作为重建图像的像素值。为了降低计算成本并确保重建的统计等效性，常使用高斯金字塔或拉普拉斯金字塔进行多分辨率合成[14]。本研究选择使用较为常用的高斯金字塔，其由连续的滤波和下采样操作构建而成。

纹理合成整体过程如图1所示，首先针对金相照片进行阈值化、滤波等一系列图像预处理，获得输入图像样本。其次使用因果邻域学习图像中像素的分布，获得图像邻域数据集合，并按照光栅扫描的顺序逐像素重建。最后利用高斯金字塔将不同分辨率的图像堆叠生成重建结果，其中最低分辨率与最高分辨率的图像分别位于金字塔的顶部与底部。

图1 纹理合成过程Fig.1 Texture synthesis process

1.2 算法优化

在纹理合成算法重建过程中是根据原始图像邻域中像素的相似性来确定输出像素的值，所以无法准确控制图像中不同相的占比，另外，算法本身需确定合适的邻域尺寸，远小于邻域尺寸的颗粒易被忽略，致使重建结果中的颗粒数量少于原始图像。为此，本文在原有纹理合成的基础上进行了优化，针对重建后的图像加入颗粒补充与面积分数调整步骤。优化过程流程图如图2所示，输入i+1 相材料的重建图像，针对其中颗粒尺寸较小的相，参照原始图像中该相的颗粒数量，随机填充单像素颗粒至图像中。随后提取其中的phase1 进行面积分数调整，利用轮廓识别算法根据phase1 的占比误差沿边缘位置进行像素加减。按照此过程对图像中的所有相进行调整后，合并单相样本并统计各相占比，满足判据则输出图像，不满足判据则将图像重新输入并继续调整，利用迭代优化保证重建结果与原始图像的各相占比近似一致。

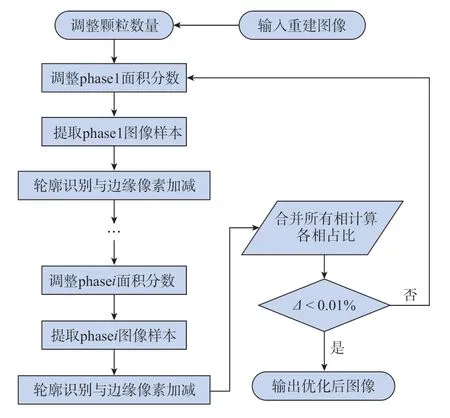
图2 优化纹理合成算法流程图Fig.2 Flow chart of optimization texture synthesis

为验证算法优化的有效性，以三相非均质AlSi-PHB 封严涂层为研究样本开展研究。该涂层由金属基体相铝硅（AlSi）、非金属润滑相聚苯酯（PHB）和孔隙组成[15]。图3（a）为尺寸500×500 像素的AlSi-PHB封严涂层典型金相照片，其中白色部分为AlSi 相基体，灰黑色部分为PHB 相，其在涂层内呈网状随机分布，尺寸在10～150μm 之间，黑色部分对应孔隙，主要聚集在聚苯酯周围，小孔呈近似圆形，大孔形貌不规则，尺寸范围5～80μm。

对图3（a）进行二维重建，优化前后纹理合成算法重建结果分别如图3（b）和（c）所示。观察可知，优化后算法重建效果整体较好，部分相在形态细节上存在差异。以孔隙为例，利用图像处理软件Image-Pro Plus 中的平均颗粒直径统计函数统计孔隙的直径D，D为以2°间隔测量所有通过颗粒质心的直径的平均长度，优化后图像与原始图像的统计结果见图4。可知，优化后图像与原始图像的孔隙颗粒直径平均值分别为20.84μm 和18.30μm，二者之间相差2.54μm。这种差异与纹理合成优化算法的原理有关，优化算法利用边缘轮廓识别与像素加减方式进行面积分数调整，可能会造成某些颗粒的边缘部分被填充，导致尺寸较优化前偏大。进一步考察了优化前后单个孔隙的形态和尺寸，如图5所示，优化前某孔隙的直径D为24.18μm，优化后为26.32μm，偏大了约2μm。

图3 AlSi-PHB 封严涂层二维微观结构及重建结果Fig.3 Two-dimensional microstructure and reconstruction results of AlSi-PHB sealing coating

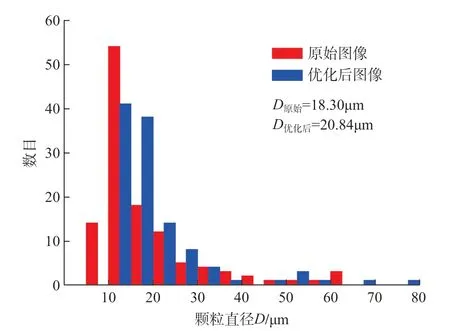
图4 AlSi-PHB 封严涂层孔隙直径统计结果Fig.4 Statistical results of pore diameter of AlSi-PHB sealing coating

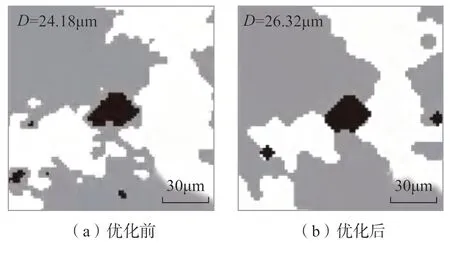
图5 优化前后孔隙形貌及尺寸Fig.5 Morphology and size of pore before and after optimization

统计了原始图像及重建结果的各相占比，详见表1。可以看出，优化前重建AlSi 相占比的绝对误差为2.8%，PHB 相为5.3%，孔隙为2.5%；优化后各相占比误差明显减小，与原始图像一致性好。后续进一步利用相关函数从统计学角度评价优化算法的有效性。

表1 原始图像及重建结果各相占比（面积分数）Table 1 Components of original image and reconstruction results(area fraction) %

1.3 相关函数

相关函数中包含了材料各相的占比、尺寸、均匀性等信息，可用于对重建结果图像质量的评价。在概率空间V中将介质划分为两个不相交的随机集合或相，表示为V1相和V2相，两相的占比分别为φ1和φ2，其中φ1+φ2=1.0。对于给定的微观结构，坐标x∈V处的指示函数I(i)(x)定义为随机变量[16]：

两点相关函数定义为I(i)(x1)与I(i)(x2)乘积的数字期望，表示为

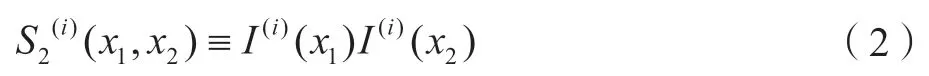
式中，尖括号为线性期望运算符。两点相关函数可视为位置x1、x2上的两个点都在相i内的概率，需要注意的是，式（2）一般适用于有任意多相的微观结构。对于均质且各向同性的介质，两点相关函数S2(i)(r)仅与任意两点位置之间的标量距离相关，其中r=|x1-x2|。

根据以上定义，如图6所示，两点相关函数具有以下特性[17]：

图6 面积分数为16% （φi=0.16）的相i 两点相关函数示意图Fig.6 Illustration of two-point correlation functions for 16%phase i (φi=0.16)

（1）如果r=0，则S2(i)(r)等于材料相i的面积分数，即S2(i)(0)=φi；

（2）如果r→∞，则S2(i)(r)接近相i面积分数的平方，即S2(i)(r)=φi2；

（3）从原点到相关函数曲线的最小距离所对应的横轴坐标值r表示颗粒尺度，r越大，则颗粒平均尺寸越大。

后续需根据原始图像与重建结果的两点相关函数误差来评价重建质量，采用的方差计算公式为，

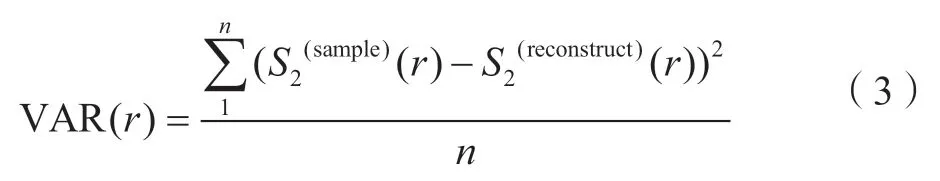
式中，S2(sample)(r)为原始图像的两点相关函数；S2(reconstruct)(r)为重建结果的两点相关函数；n为两点相关函数的长度。

2 结果与讨论

2.1 优化算法有效性评价

针对图3（a）封严涂层原始图像，用上述优化前后的算法各重建10 组模型，对重建结果中的PHB 相和孔隙计算对应的两点相关函数、平均两点相关函数及方差，结果分别见图7和8。

由上文可知，两点相关函数曲线的零点值与末端值可衡量重建结果中所含相的占比，从原点到曲线的最小距离所对应的r可衡量颗粒尺寸。以PHB 相为例，其占比为43.3%（表2），图7（a）中两点相关函数的零点值S2(PHB)(0)与末端值S2(PHB)(∞)均偏离实际值很远，且10 组曲线分散程度大，表明重建结果之间的统计一致性差。图7（b）中曲线的零点值与末端值均接近实际值，且曲线的波动较小，表明重建结果的面积分数接近原始图像，同时具有很高的统计一致性。对比图7（c）中的平均两点相关函数曲线发现，优化后重建结果的面积分数及结构均与原始图像非常接近，远优于优化前。优化后算法的方差为1.6×10-5，远低于优化前的方差6.6×10-3，表明优化后纹理合成重建结果与原始图像之间具有较好的统计等效性。

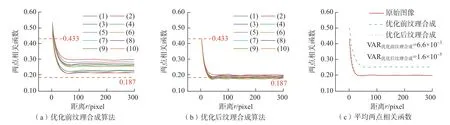
图7 重建结果中PHB 相的两点相关函数（PHB 相占比为43.3%）Fig.7 Two-point correlation function of PHB phase in reconstructed image (43.3% of PHB phase)

图8是重建结果中孔隙的两点相关函数，观察图8（a）可知，优化前两点相关函数的零点值S2(PHB)(0)与末端值S2

图8 重建结果中孔隙的两点相关函数（孔隙占比为3.9%）Fig.8 Two-point correlation function of pore phase in reconstructed image (3.9% of pore phase)

(PHB)(∞)均偏离实际值很远，表明优化前重建结果中孔隙占比偏低。优化后的孔隙占比接近实际值，较优化前明显提升（图8（b））。由于优化算法是通过像素加减实现各相面积分数调整，图8（b）中10 组重建结果的孔隙形态存在差异，导致其统计一致性略有下降。图8（c）中优化后算法的重建结果与原始图像的曲线较为相似，且方差小于优化前，表明重建结果中孔隙的统计等效性较好。在此基础上，针对研究样本，利用优化后的纹理合成算法进行微观结构的表征与重建。

2.2 微观结构重建结果

选取两张AlSi-PHB 封严涂层的金相照片作为原始图像样本，样本1 的各相占比为φ（AlSi）=51.1%、φ（PHB）=44.7%、φ（Air）=4.2%，样本2 的各相占比为φ（AlSi）=51.1%、φ（PHB）=47.0%、φ（Air）=1.9%，使用优化后纹理合成算法针对两张样本分别重建10 张图像，滤波后原始图像及对应的重建结果如图9所示。

图9 封严涂层原始图像及重建结果Fig.9 Original image and reconstruction results of seal coating

2.3 重建结果评价

计算两个样本重建结果与原始图像的两点相关函数，得到PHB 和孔隙两相的平均两点相关函数，并与原始图像的结果进行对比，分别见图10和11。

以样本1 为例，观察图10（a）与（b）可知，优化后纹理合成算法重建结果与原始图像的曲线零点值和末端值均较为接近，说明重建结果的PHB 和孔隙两相占比准确。图10（a）中示出了重建结果曲线距原点最近时的横轴坐标值r1（红色）与原始图像所对应的r0（黑色），r1略大于r0，说明重建结果中PHB 相的平均尺寸略大于原始图像。图10（b）中重建结果的r1与原始图像的r0几乎重合，说明重建结果中孔隙的平均尺寸与原始图像基本一致。计算得到PHB 和孔隙两相的两点相关函数的方差分别为6.9×10-5与1.9×10-7，说明重建结果与原始图像整体匹配较好。

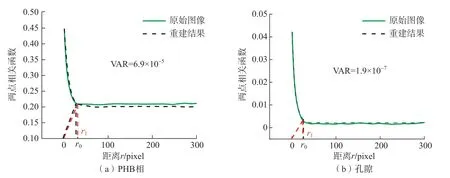
图10 样本1 重建结果的平均两点相关函数（PHB 相占比为44.7%，孔隙占比为4.2%）Fig.10 Average two-point correlation function in the reconstructed image of sample 1 (44.7% of PHB phase and 4.2% of pore phase)

同理分析可知，图11（a）与（b）中样本2 重建结果中各相占比准确，其中PHB 相的平均尺寸略大于原始图像，孔隙的平均尺寸接近原始图像，方差分别为8.8×10-5与1.3×10-7。

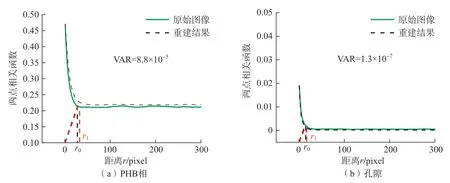
图11 样本2 重建结果的平均两点相关函数（PHB 相占比为47.0%，孔隙占比为1.9%）Fig.11 Average two-point correlation function in reconstructed image of sample 2 (47.0% of PHB phase and 1.9% of pore phase)

综上所述，基于优化后纹理合成算法获得的AlSi-PHB 封严涂层重建结果与原始图像之间具有较好的统计等效性。需要说明的是，该涂层以AlSi 相作为基体，在重建过程中AlSi 相被视为空白画布，通过分析填充相PHB 相与孔隙的重建误差即可间接反映AlSi 相的重建质量，因此，文中没有对AlSi 相的重建结果进行评价。

纹理合成优化算法是利用边缘轮廓识别与像素加减方式进行各相占比调整，通过调节颗粒的形态与尺寸达到面积分数优化的目的，并通过颗粒补充的方式修正优化带来的颗粒尺寸误差，影响重建结果的因素有颗粒尺寸、形状及分布等。优化算法通过补充单像素尺寸颗粒使重建前后颗粒数量一致，仅补偿了少量的像素数，剩余的需填充像素通过随机方式覆盖至颗粒的边缘，导致平均颗粒尺寸偏大且颗粒形状略有差别。此外，重建过程根据原始图像邻域中各相出现的概率来确定输出像素的值，对于占比相对较低的相，如本文中占比小于5%的孔隙，其对应邻域被选择的概率较低，易导致重建图像中孔隙占比低于实际值，经调节颗粒形态尺寸实现面积分数一致的同时，可能引起重建结果中孔隙平均尺寸偏大。

3 结论

（1）针对现有纹理合成算法无法准确控制重建结果中各相占比的问题，利用颗粒补充、像素加减与边缘搜索进行算法优化，提出了一种面积分数可控的MCR纹理合成算法。结果表明，该算法可在保证材料结构的基础上实现各相占比一致的准确重建。

（2）将优化后纹理合成算法应用于多相非均质材料AlSi-PHB 封严涂层的二维MCR，结合两点相关函数对重建结果进行表征与评价，表明重建结果与原始图像具有较好的统计等效性。