压电振动能量收集器的建模与响应分析

冯逸亭，刘文光，方孟翔，吴兴意，高铭阳，陈红霞

(南昌航空大学 航空制造工程学院,江西 南昌 330063)

0 引言

随着无线传感器网络与便携式电子移动设备的飞速发展，其应用涉及建筑、机械、车辆、航空航天等领域[1-3]。然而，如何为系统提供充足持久的电能供应成为研究者需要解决的问题。振动是常见的一种能量形式，如飞机飞行过程中机翼的振动、车辆运转及大型机械作业时产生的振动等[4-5]。因此，研究振动能量收集技术对于解决无线传感器与便携式电子移动设备的供电问题具有重要意义。

振动能量收集技术主要有电磁式、静电式及压电式3类[6-8]。其中，压电式振动能量收集器由于结构紧凑，无电磁干扰及易于微型化等优点成为研究者关注的焦点。目前，国内外研究者相继研发了多种构型的压电振动能量收集器。刘祥建等[9]提出了一种Rainbow型压电能量转换结构，实现了多个方向载荷作用下低功耗电子器件的供能。Zhang等[10]设计了一种弧形压电双稳态振动能量采集器，采集器运用磁耦合构建出双稳态结构以提高能量收集效率。闫丽等[11]建立了双端固支式压电能量收集器的机电耦合振动模型，发明了梯形梁结构以降低谐振频率和提高发电电压。Nie等[12]将L型悬臂梁和压电材料的非线性引入能量收集器，拓宽了振动能量收集器的频带范围。Karadag等[13]设计了一种新型智能压电振动能量收集器，它能自动调整自然频率以维持系统共振、拓宽能量收集器的频带。Samah等[14]考虑悬臂梁的线性和二次形状变化，设计出能够在低频振动环境下产生有效电能的压电俘能结构。Juil等[15]提出了尖端激励压电收集器的新结构，通过形状优化提高了能量收集器的最大输出功率。

虽然研究者对压电能量收集技术做了大量探索工作，提出了许多压电收集器的结构，通过新构型及新方法提高其工作效率，但是多数研究局限于单方向振动模式，并普遍存在频带较窄的不足。实际应用中，外界振动具有多维度、随机性及非线性等特点，只有合理设计压电振动收集结构才能最大程度提高其电学输出特性。因此，本文设计了一种多方向压电能量收集器，不仅可以收集利用多个方向的振动能量，且引入了非线性磁力以实现自主调谐功能，拓宽了工作频带。对所设计的能量收集器建立机电耦合模型，利用COMSOL软件建立能量收集器的有限元模型，仿真分析了不同结构参数下系统的电学响应特性。

1 动力学建模

1.1 压电振动能量收集器结构

图1为本文设计的多方向压电振动能量收集装置结构示意图。

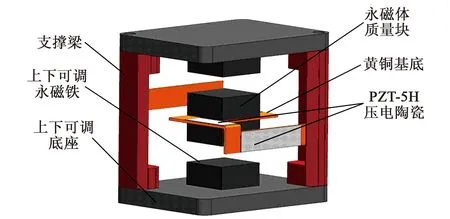
图1 多方向压电能量收集装置结构示意图

能量收集装置由上下可调底座、上下可调永磁体、支撑梁、黄铜基底、永磁体质量块及PZT-5H压电陶瓷构成。其中，由螺旋状黄铜基底和上下表面黏附的永磁体质量块一起组成了能量收集装置的振动系统，通过基底两端与支撑梁侧面固定连接。将4片压电片分别粘贴于螺旋固支梁表面构成压电振子。在两个底座中心分别固定安装方形永磁体，通过移动上下可调底座控制磁间距。整个压电振动能量收集装置呈现中心对称而非轴对称状态，这使其受到外界激励时弹簧基体发生扭转变形，造成螺旋梁拐角处的应力集中现象。因此，在“L”型拐角处倒半径为1 mm圆角，避免应力集中导致结构破坏。这种压电振动能量收集装置结构的空间占有率小,结构集成度高，可以同时收集横向及纵向振动能量，并利用永磁体间的相互作用达到自主调谐的目的，提高了能量收集效率。

当装置受到外界激励时，振动系统将以永磁体质量块为中心做横向或纵向摆动。螺旋状式基底可以起到平面弹簧的作用，产生振动与应变。此时粘贴于基底表面的PZT-5H压电陶瓷利用正压电效应将基底产生的振动与应变转化为电能。

1.2 机电耦合动力学建模

为分析方便，多方向压电能量收集器的振动系统在受到质量块重力F0作用下，其一阶模态振动模型可简化为图2所示的两端固支梁结构。

图2 结构一阶振型简化示意图

假设系统等效质量为Meq，等效刚度为Keq，等效阻尼系数为ceq。系统振动时，Z(t)为振动位移，α为机电耦合系数，RL为等效负载电阻。图3为能量收集器直接外接电阻作为负载时的集中参数等效模型。

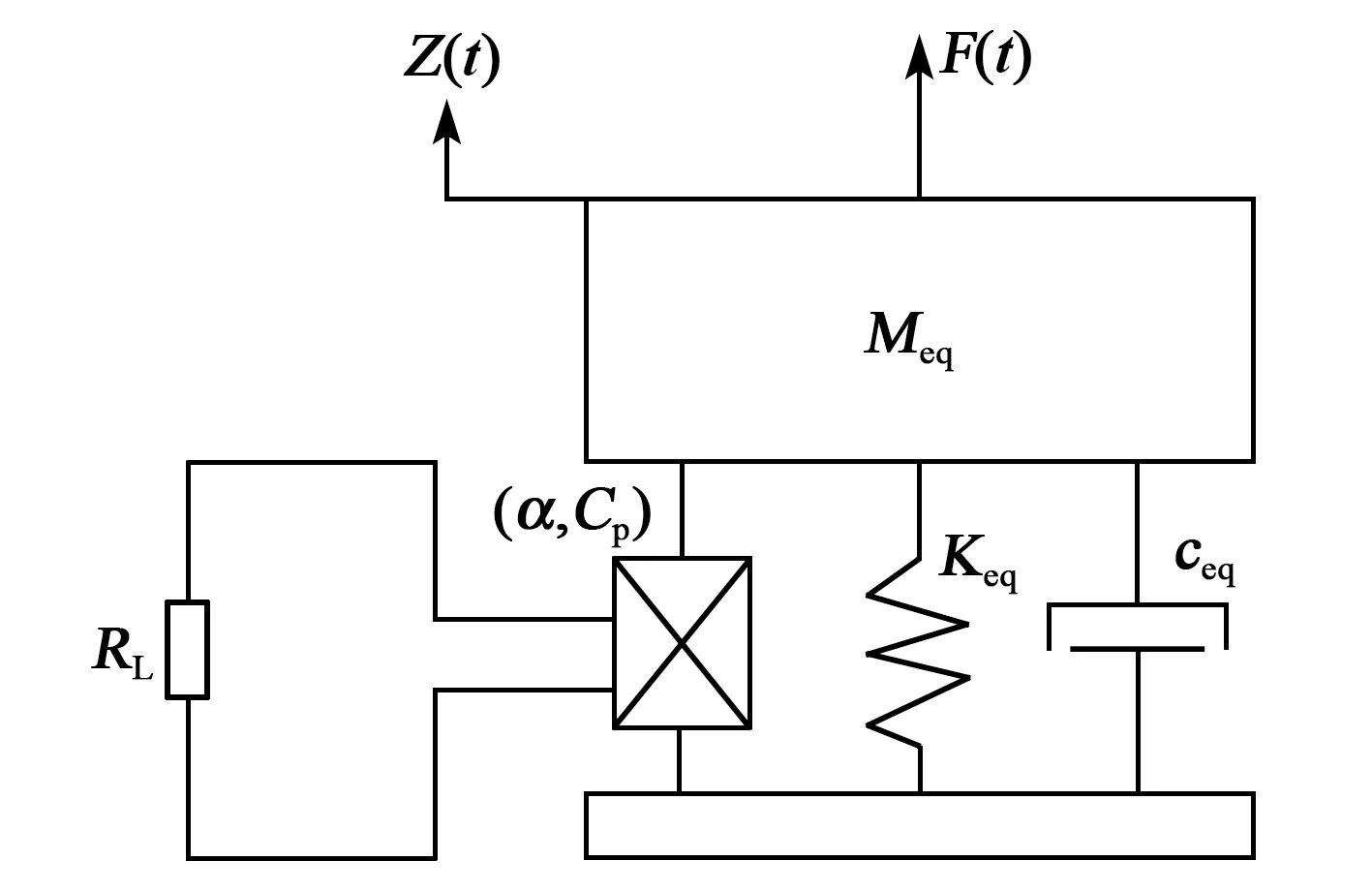
图3 外接纯电阻时能量收集器的集中参数等效模型

当外界激励F(t)作用于能量收集器时，系统会产生相应的振动，导致质量块两侧的压电振子弯曲变形，表面将输出电压，即RL两端电压V0(t)。由牛顿第二定律可导出系统压电振子的动力学方程：

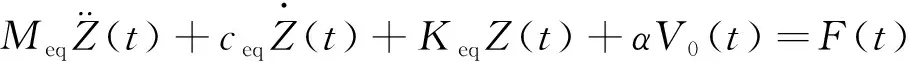
(1)

其中：

(2)

式中：βM,βK分别为质量阻尼和刚度阻尼；mp,mb及ma分别为压电陶瓷片、基底及永磁体质量块的质量；l,lp分别为基底和压电陶瓷片的长度；hp,h分别为压电陶瓷片和基底的厚度；w为基底宽度；Ep,Eb分别为压电陶瓷片和基底的弹性模量。

文献[16]研究表明，压电振动能量收集器可等效为电流源与外接电阻RL的并联。因此，根据基尔霍夫定律，电路中的回路电流满足：

(3)

式中Cp为等效电容。

联合式(1)、(3)可得外接纯电阻负载时压电振动能量收集器的机电耦合方程。求解方程组可得压电振动能量收集器的振动模态和电学输出特性，并分析不同结构参数(如结构刚度、外接负载阻值及附加质量等)对系统电学响应的影响。考虑到振动能量收集器结构的复杂性及实际振动过程的多变性，直接求解方程组分析结构力学性能较难，本文采用COMSOL多物理场仿真软件对多方向压电振动能量收集器进行分析，探究了系统电学响应特性。

2 响应分析

2.1 振动模态

为提高振动能量收集器的电学响应特性，设计时必须了解系统的振动模态[17]。由于系统的模态频率和电学响应等特性主要由平面弹簧、PZT-5H压电陶瓷及永磁体质量块集成的振动系统决定，因此，在构造能量收集器模型时需做出合理简化，以提高仿真计算效率。表1为压电振动能量收集器简化模型的主要结构参数。图4为简化后的压电振动能量收集器的有限元仿真模型。

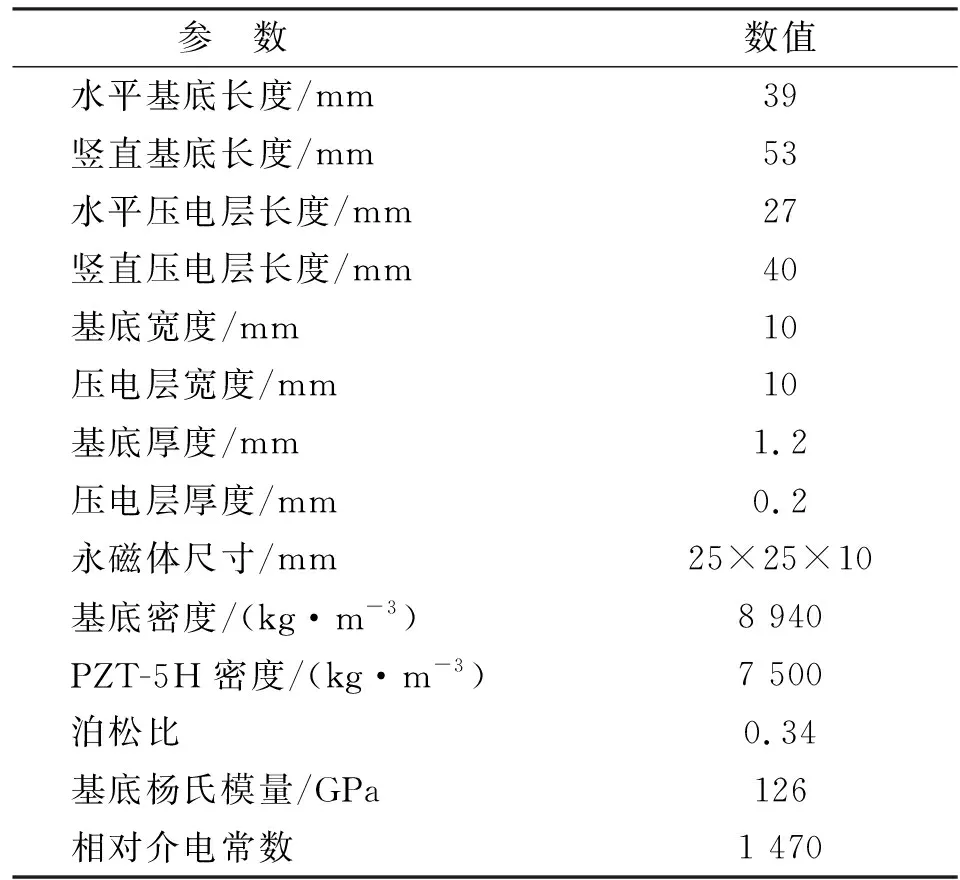
表1 多方向压电振动能量收集器结构参数

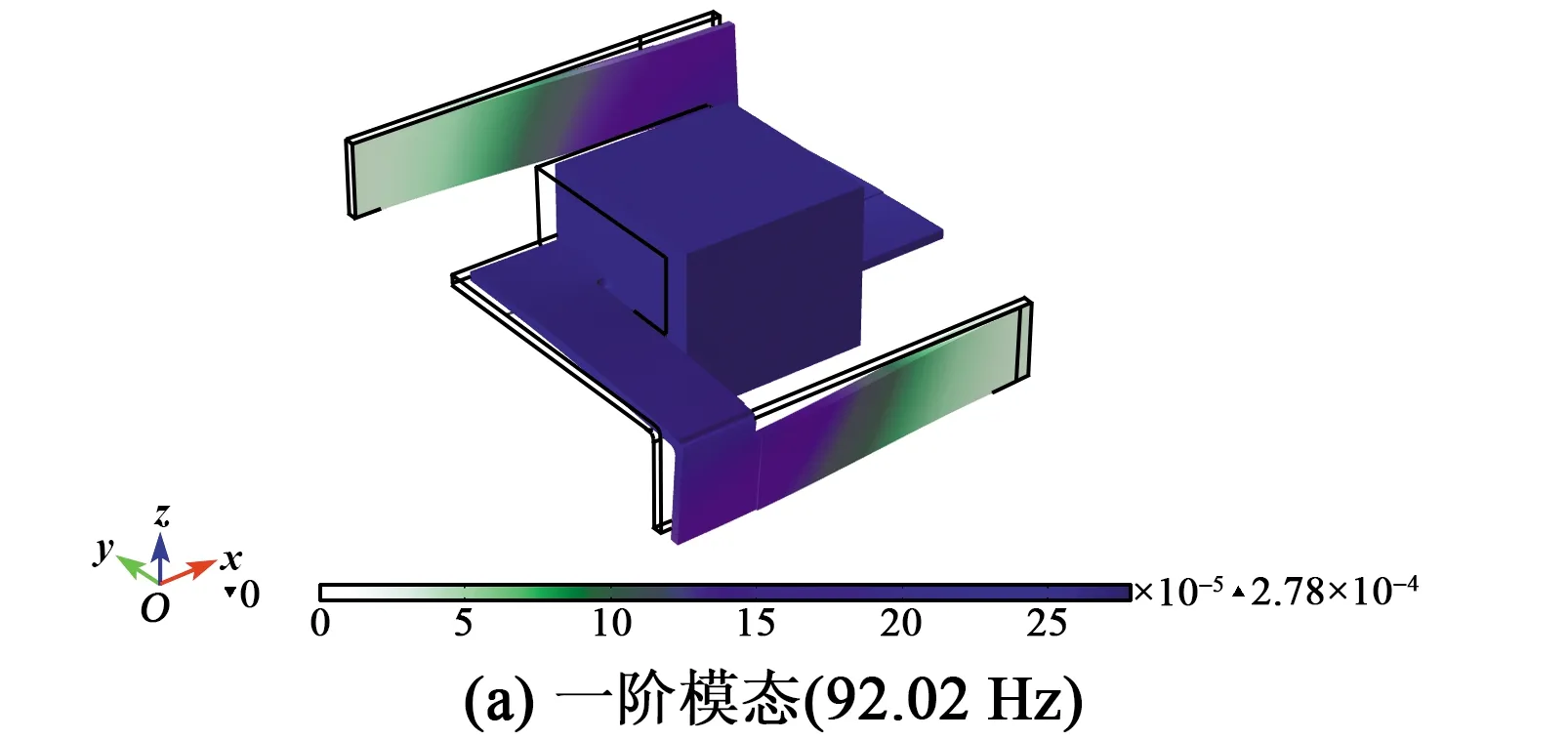
以压电振动能量收集器有限元模型(见图4)为对象进行模态分析。在网格划分时，对压电层进行细化的网格划分，而其余部分采用常规的网格划分，以确保满足收敛性的同时减少计算时间。通过分析计算得到压电振动能量收集器的前三阶振动模态(见图5)，结果表明，一、二阶模态谐振频率分别为92.02 Hz和114.09 Hz。在前两阶模态下，系统主要以永磁体质量块为中心、沿着z方向上下振动。此时，振动系统的几何中心处位移最大，沿着平面弹簧向外逐渐减小。三阶模态谐振频率为170.31 Hz，振动系统沿几何中心做旋转运动，平面弹簧只在靠近中心部分有少量位移，其余部分均无变形。振动能量收集过程中，应避免这种状况出现，主要利用一阶谐振频率92.02 Hz附近的振动能量，以便在较低的谐振频率下获得更好的电学响应特性。

图4 振动系统有限元模型

2.2 电学响应

为了探讨各参数对压电振动能量收集器电学响应的影响，分析时将两条螺旋梁的端部设置为固定约束，分别沿z、y轴两个方向对整个振动系统施加1g(g=9.8 m/s2)加速度体载荷，外接负载电阻(100 kΩ)以模拟开路条件，计算频域范围为88～96 Hz，得到负载电压、负载功率随频率的变化情况，如图6、7所示。

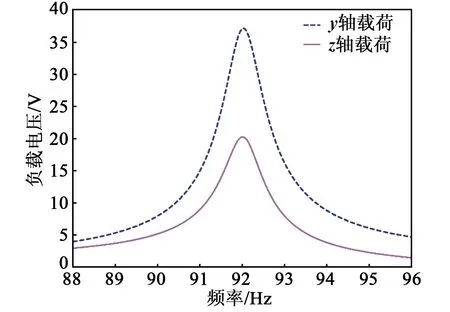
图6 y、z方向负载电压频域响应

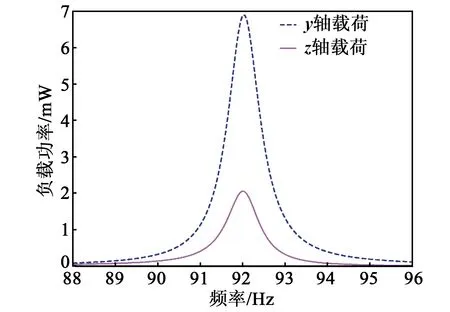
图7 y、z方向负载功率频域响应

由图6、7可知，分别从y、z两个方向施加载荷时，负载电压和功率都在振动系统的一阶谐振频率92.02 Hz处取得最大值，并且在y方向的载荷激励下压电振动能量收集器具有更好的电学响应效果，负载电压峰值可达37 V，最大负载功率为6.9 mW。因此，在实际应用中应加大对y方向振动的利用，以提高能量收集效率。

采用单一变量原则，设置z方向的1g加速度体载荷作为外界激励，图8～10为不同结构参数下压电振动能量收集装置的频域响应情况。具体结果如下：

1) 由图8可知，当压电层厚度不断增加时，振动系统的刚度随之变大，振幅逐渐减小，导致压电单元受到的应变降低。负载电压频域响应的谐振频率向右移动，从88.4 Hz增至99.4 Hz，负载电压峰值由24 V降至18 V。因此，为了在较低谐振频率下获得较高电压输出，应在满足压电层强度的条件下选用厚度较薄的压电陶瓷。

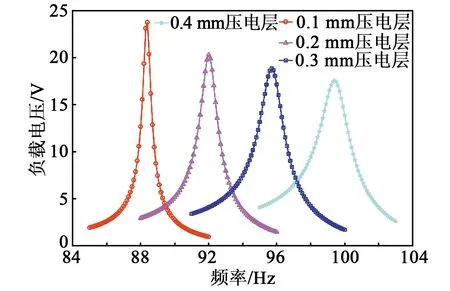
图8 压电层厚度对负载电压频域响应的影响

2) 由图9可知，基底厚度的改变对振动系统的共振频率及负载电压有较大的影响。当基底厚度由1.0 mm增至1.3 mm时，共振频率由72.8 Hz大幅增至112.1 Hz，同时，负载电压幅值也由30 V降至17 V。可见随着基底厚度的增加，平面弹簧刚度明显增大，使得压电单元输出效率降低。

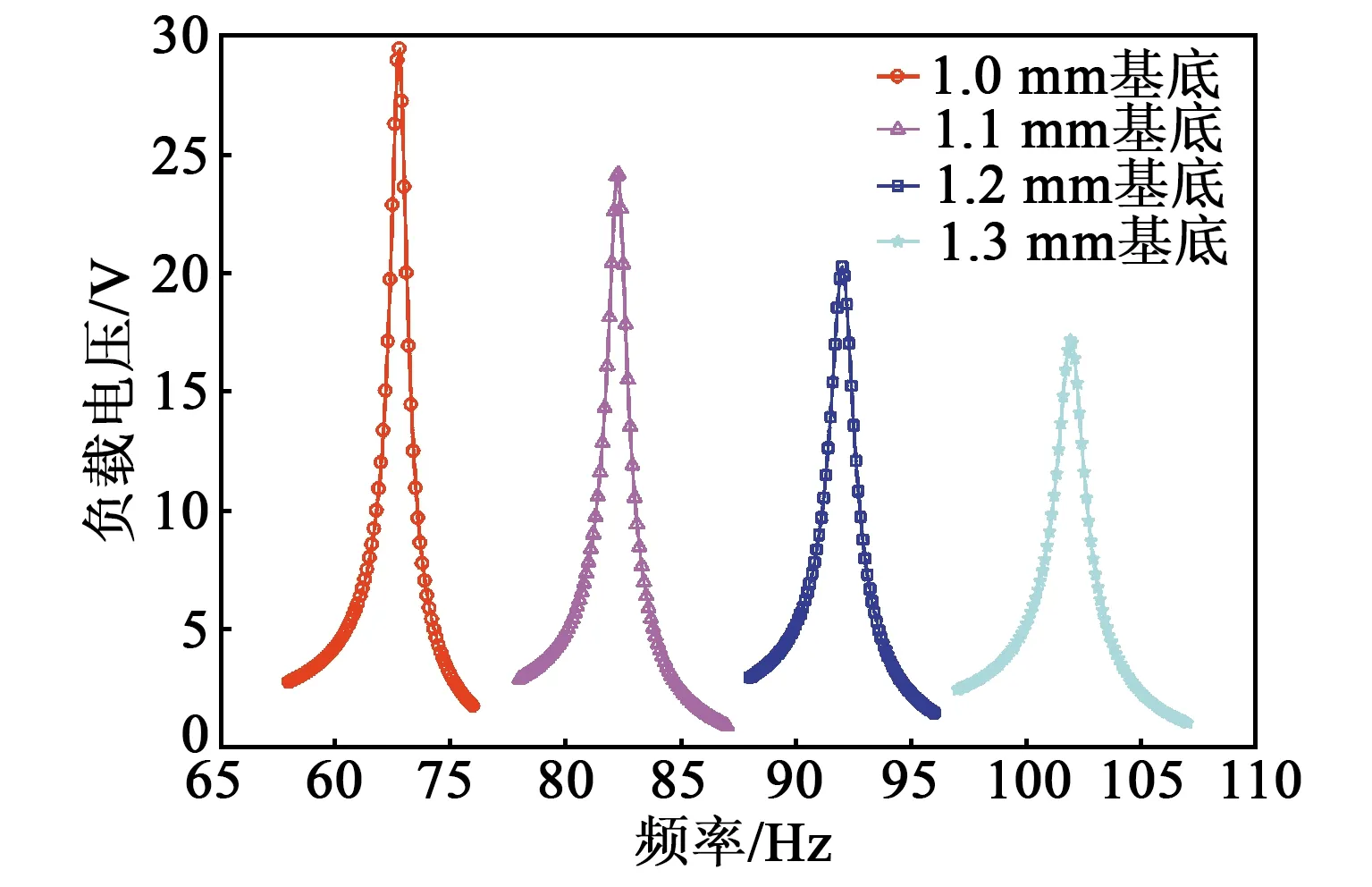
图9 基底厚度对负载电压频域响应的影响

3) 由图10可知，永磁体厚度的改变实际上是对振动系统附加质量的增减，永磁体厚度的增加伴随着谐振频率的降低及输出电压的升高，故增加附加质量更有利于提高振动能量的收集效率。

图10 永磁体厚度对负载电压频域响应的影响

在压电俘能系统中，外接负载阻抗匹配可以有效增加能量输出，下面进行主要结构参数的负载功率阻抗匹配分析，使压电能量收集器的输出功率达到最大化。图11～13为不同厚度对负载功率-阻抗匹配的影响。具体结果如下：

1) 由图11可知，随着压电层厚度的增加，最大输出功率呈现下降趋势，由10.7 mW降至5.4 mW；同时阻抗匹配随之增加，由5 kΩ增大至20 kΩ。负载的增加意味着更多的能量耗散，不利于振动系统对于外界能量的收集。

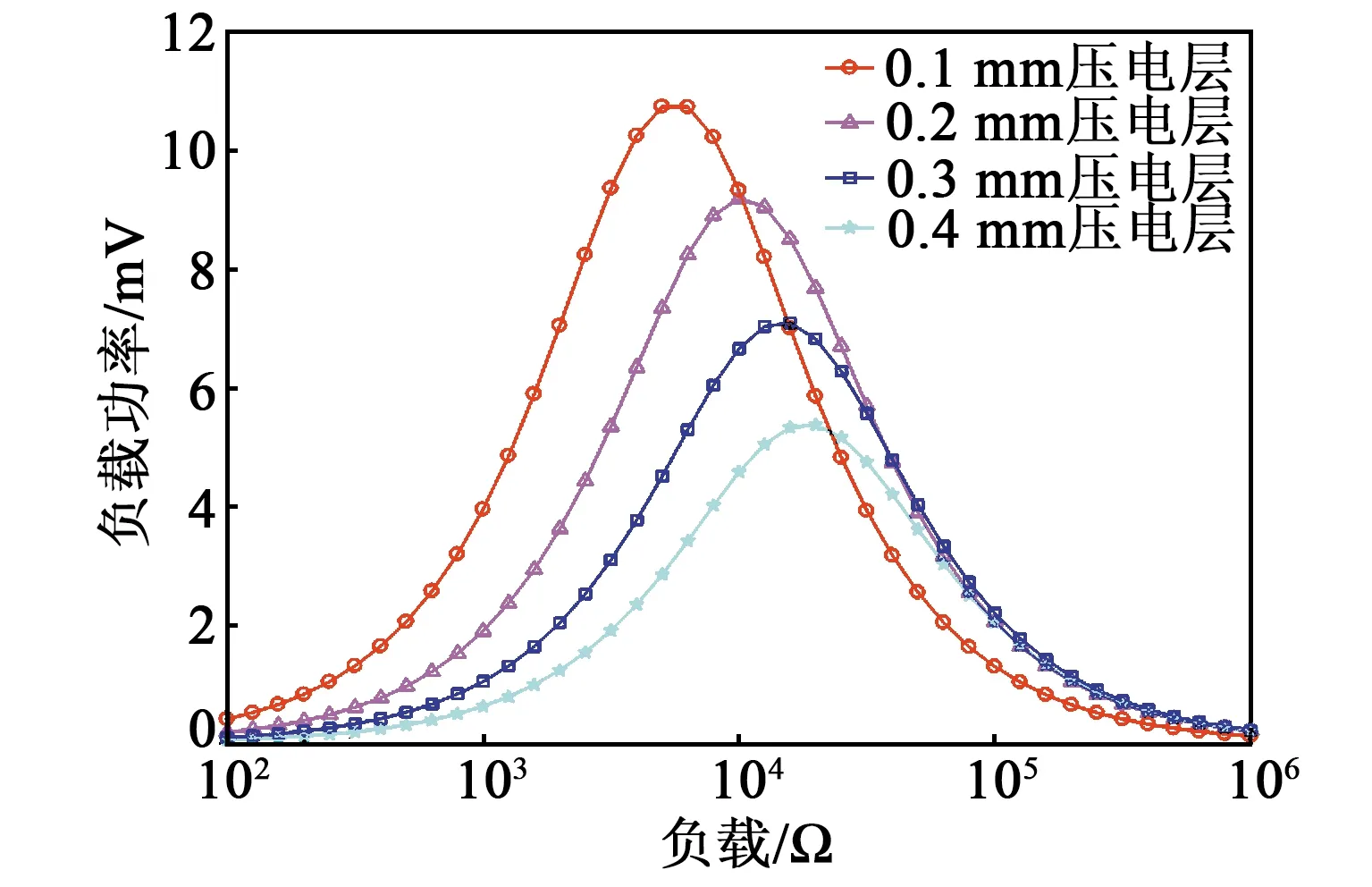
图11 压电层厚度对负载功率-阻抗匹配的影响

2) 由图12可知，基底厚度对最佳负载的影响较小，而对功率幅值的影响较大。随着基底厚度的增加，匹配阻抗略微减少，且都集中于10 kΩ附近，负载功率幅值降低了50%。

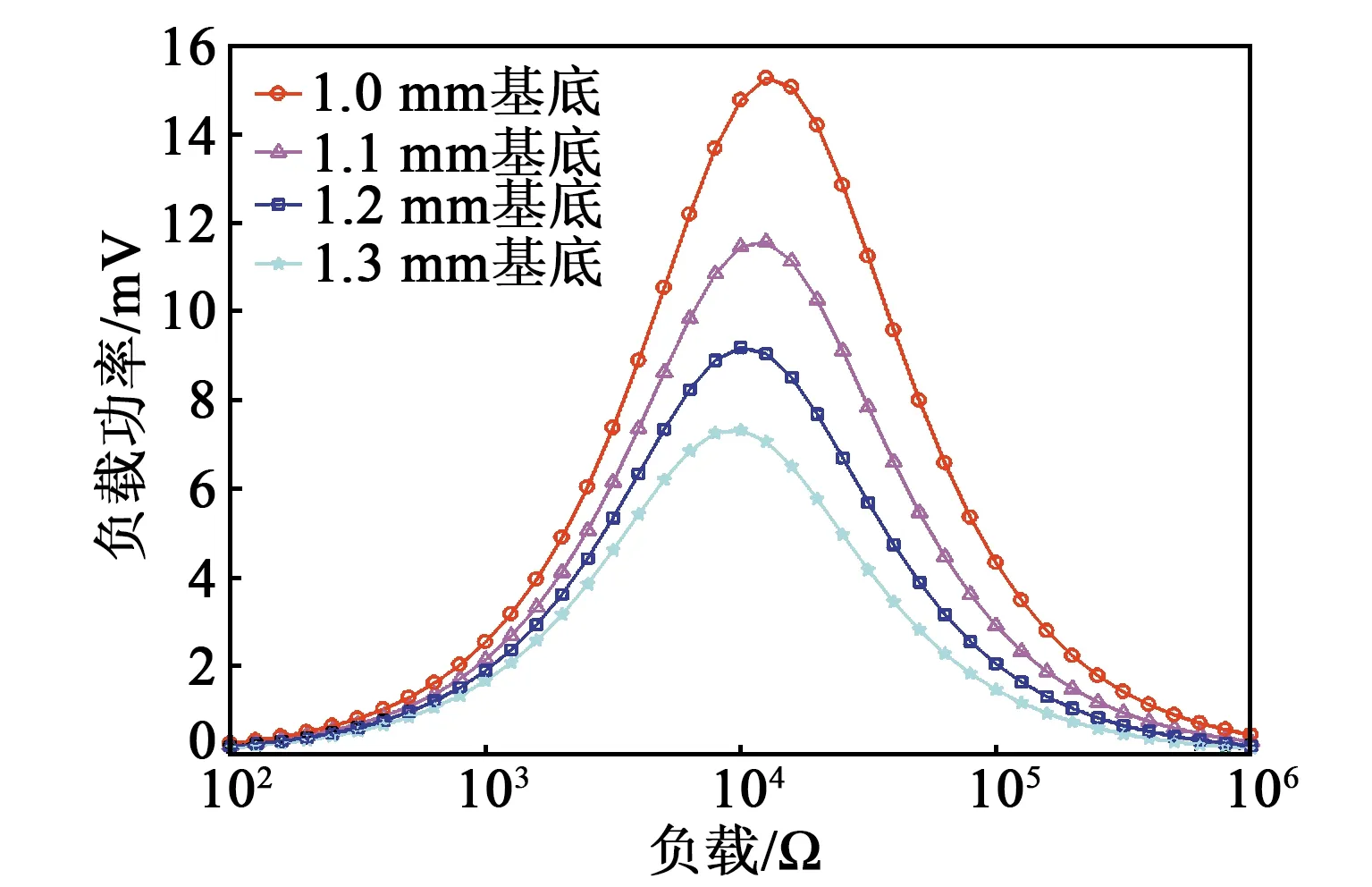
图12 基底厚度对负载功率-阻抗匹配的影响

3) 由图13可知，永磁体厚度即附加质量的增加对负载功率幅值影响呈正相关趋势，但对最佳阻抗匹配阻值无影响，最佳负载均为10 kΩ。

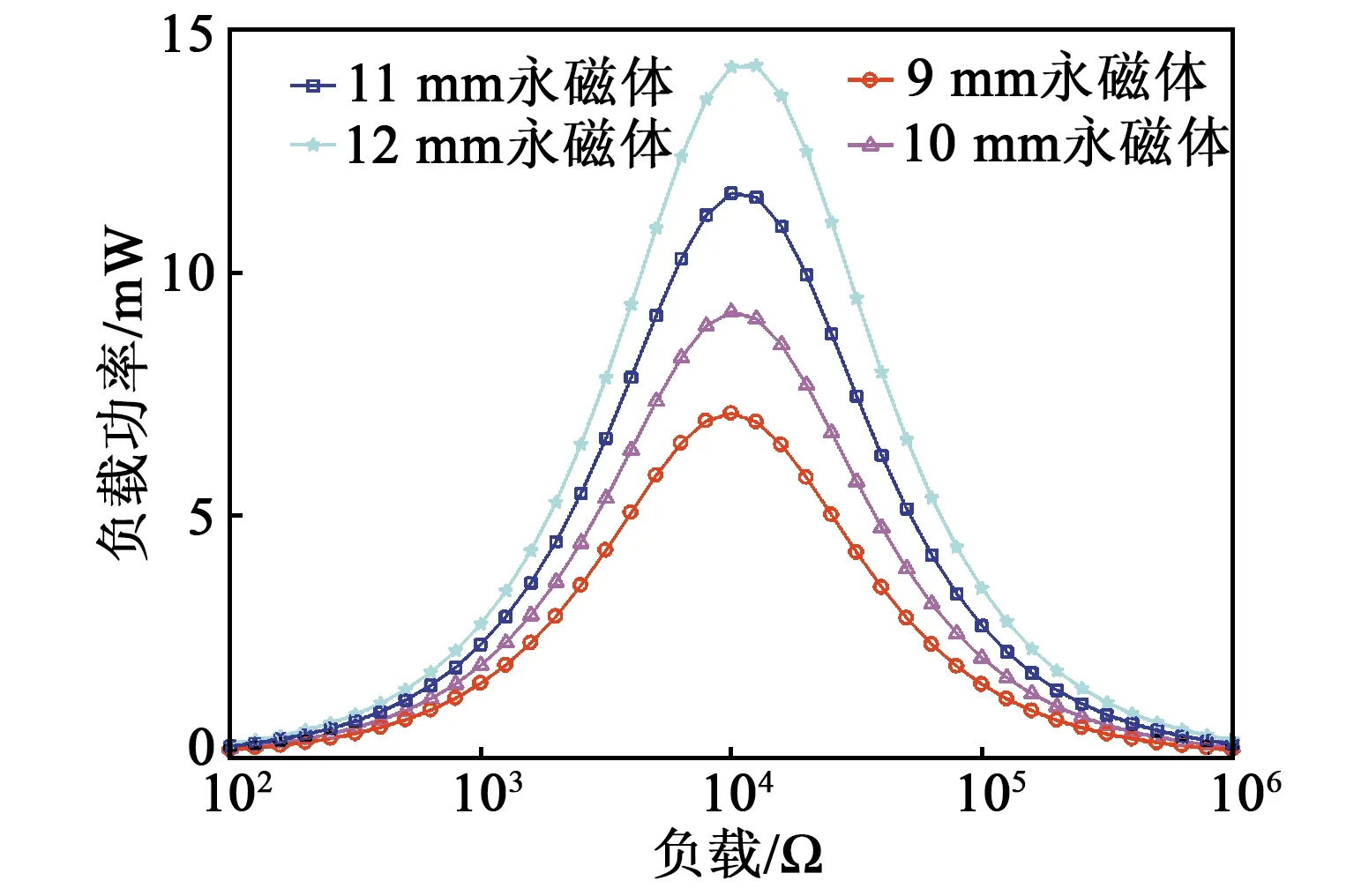
图13 永磁体厚度对负载功率-阻抗匹配的影响

为了研究非线性磁力对压电能量收集器电学输出特性的影响，在仿真实验原有的物理场中加入磁场作用。设置下方磁体对振子磁体的作用力为吸力，上方磁体对振子磁体作用力为排斥力，由此形成竖直向下的磁场(见图14)。首先计算相邻永磁体之间的磁力作用，然后将磁力作为边界载荷以正弦形式加载到振动系统中。通过改变磁间距d，分析了不同磁力下压电能量收集器的频域响应情况(见图15)。由图可知，压电能量收集器引入竖直向下的磁场后负载电压略有下降，但随着永磁体间距的减小，负载电压只有轻微的降低，而共振频率增高。据此规律，根据外界激励调节磁间距大小可拓宽装置工作频带，以适应不同环境下的振动频率。

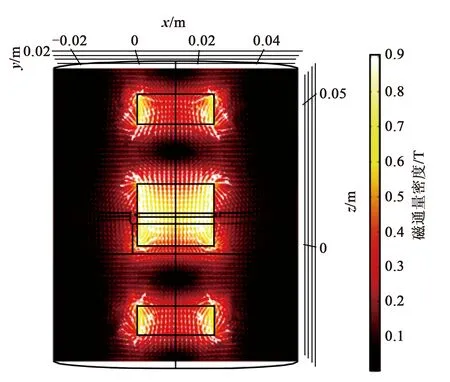
图14 永磁体间磁力计算模型

图15 不同磁间距对负载电压频域响应的影响

3 结论

设计了一种多方向压电振动能量收集器的结构，建立了系统的机电耦合动力学模型，分析了不同结构参数对能量收集装置负载电压及负载功率阻抗匹配的影响，并引入非线性磁力实现自主调谐功能。主要结论如下：

1) 基底和压电层厚度的减小伴随着负载电压及负载功率的增加，但永磁体质量增减与二者的变化呈负相关趋势。

2) 在负载阻抗匹配方面，压电层厚度的增加导致负载阻抗大幅增大，由5 kΩ增大至20 kΩ，而随着基底厚度的增加，最佳负载阻值略有减小且均集中于10 kΩ附近，永磁体质量对阻抗匹配阻值无影响。

3) 将磁场引入原有机电耦合场中可以改变谐振频率的大小，在对输出电压影响较小的情况下实现自主调谐，以拓宽能量收集器的频带。