单相逆变器目标函数优化控制
叶中豪,戴瑜兴,彭子舜
单相逆变器目标函数优化控制
叶中豪1,戴瑜兴1,彭子舜2
(1.温州大学电子与电气工程学院,浙江温州 325035;2.湖南大学电气与信息工程学院,湖南长沙 410082)
目标函数是智能算法优化逆变器性能的评估标准.针对逆变器的目标函数考虑不够全面,需要提高逆变器整体性能等问题,提出了一种可以反映逆变器多个性能指标(电压精度、电压的总谐波失真、逆变器的效率以及功率器件的结温性能等)的目标函数,通过智能算法有助于提高逆变器的整体性能.最后以通过粒子群优化算法优化的单相离网逆变器为例,验证了所提出的目标函数的有效性.
目标函数;逆变器;损耗分析;结温
随着能源问题的日益凸显,在新能源发电、电动汽车、家用电器等领域中逆变器性能的提升显得尤为重要.就电动汽车而言,电动机是有源负载,在汽车行驶过程中需要频繁加速和减速,并且电动汽车中的逆变装置所处环境温度较高,工作条件比一般的工况更恶劣,因而对逆变器性能提出了更高的要求,即高效、高稳定性、高功率密度等.
智能算法已广泛应用于逆变器的优化控制中,目标函数可以反映逆变器性能指标,是优化的关键.目前,逆变器的目标函数主要是降低输出电压的谐波含量.文献[1-2]通过优化脉宽调制(Pulse-Width Modulation, PWM)脉冲序列的导通角实现了逆变器特定谐波消除(Selective Harmonic Elimination, SHE).在文献[3]中,为了提高逆变器的效率,以逆变器的总损耗为最优化目标,并通过变分法和拉格朗日法对逆变器的开关频率进行了优化.文献[4]中,以光伏系统输出功率最大和输出电流谐波畸变率最小为优化目标,建立了目标函数.
目前针对逆变器性能指标的目标函数并未得到全面考虑,难以同时考虑电压的总谐波失真(Total Harmonic Distortion, THD)、电压精度、效率、半导体器件结温以及其他重要指标.为了解决以上问题,本文提出了一个可以反映变频器多个性能指标的目标函数,包括误差绝对值积分(Integral Absolute Error, IAE)函数和损耗函数.IAE函数可以反映电压精度和电压的THD值,损耗函数可以反映逆变器的效率和功率器件的结温.本文分析了调制比和开关频率对逆变器性能指标的影响,在对性能指标之间的关系进行深入分析的基础上,选择了能充分反映变频器性能指标的目标函数,最后通过粒子群优化算法(Particle Swarm Optimization, PSO)优化单相离网逆变器为例,验证了本文提出的目标函数的可行性与有效性.
1 调制比和开关频率对逆变器性能指标的影响
本文以单相离网逆变器为例,对输出电压的总谐波失真、电压精度、效率和功率器件的结温等性能指标进行具体分析,这些指标主要受调制比和开关频率的影响.
1.1 电压THD和电压精度
单相离网逆变器的拓扑结构如图1所示.
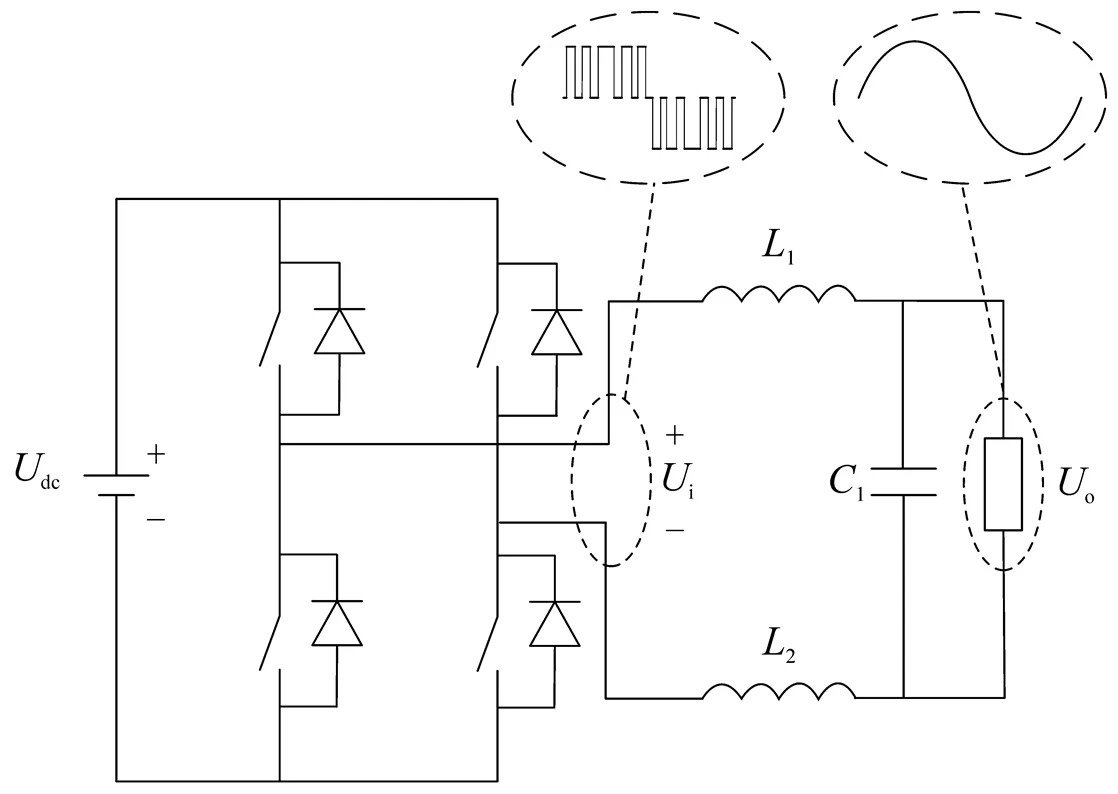
图1 单相离网逆变器拓扑
图1中i为逆变器桥臂的输出电压,o为负载两端的电压.逆变器桥臂的输出电压[5]可以表示为:
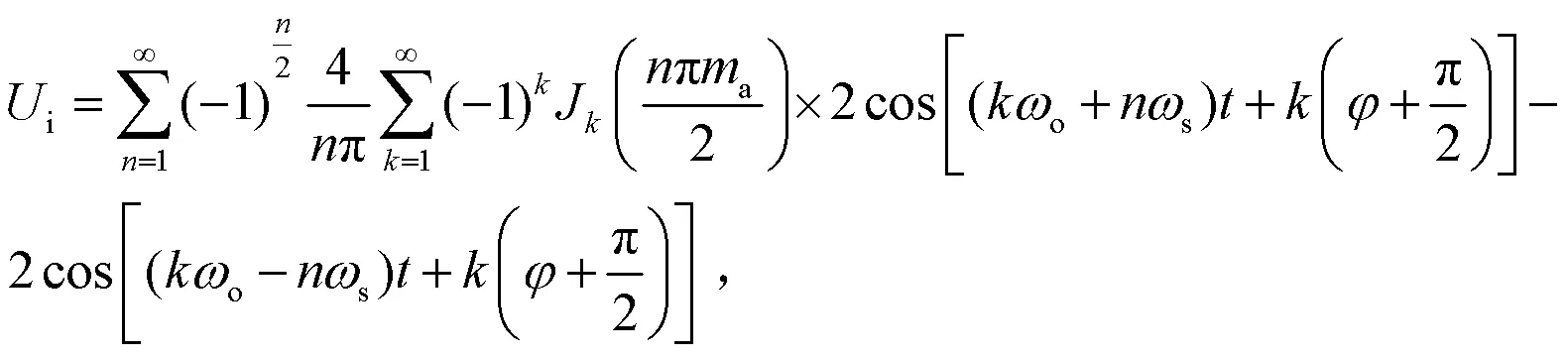
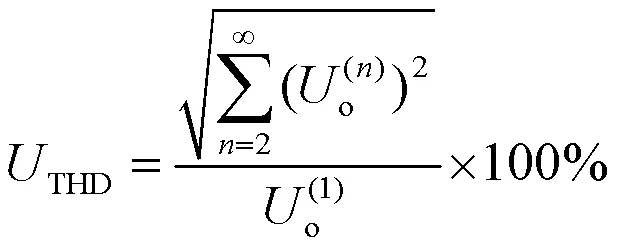
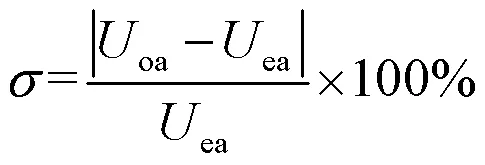
1.2 逆变器损耗
逆变器的效率与总损耗呈负相关.逆变器的损耗主要包括功率器件(SiC MOSFET和SiC SBD)的损耗以及滤波器的损耗.功率器件的损耗包括开关损耗和导通损耗(SiC肖特基二极管具有更快的开关速度和零反向恢复电流等特点,因此可以忽略其反向恢复损耗).滤波电容的损耗可以忽略不计,滤波器的损耗可以近似为滤波电感的损耗.因此总损耗的公式为:
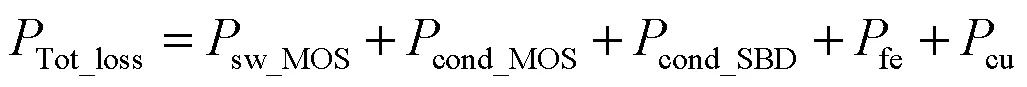
其中Tot_loss、sw_MOS、cond_MOS、cond_SBD、fe和cu分别是逆变器的总损耗、SiC MOSFET的开关损耗[6]、SiC MOSFET的导通损耗[7]、SiC SBD的导通损耗[8]、滤波器电感的磁芯损耗[9]和铜损.详细的损耗分析如表1所示.

表1 损耗分析
在表1中,D、D和sw分别代表漏源电流、SiC MOSFET两端的电压和功率器件的开关频率;on和off是SiC MOSFET开通和关断的时间间隔,可以从数据手册[10]中获得;DS,on和D() 分别表示MOSFET的导通电阻和漏源电流;F0和F分别代表阈值电压和正向传导电流,F是差分电阻;参数、和由铁氧体材料厂家的数据手册确定;eq是等效频率,与磁化速度有关;m和分别是峰值感应和复磁频率;、和cond分别表示铜的电阻率、电感绕线长度和电感线截面积,f表示交流电阻系数,由趋肤效应和邻近效应而产生.
1.2.1 变频器损耗与开关频率的关系
从表1可以看出,功率器件的开关损耗将随着开关频率的增加而增加;功率器件的导通损耗主要与导通电阻和导通电流有关,不受开关频率的影响;滤波器的电感损耗包括磁芯损耗和铜损,磁芯损耗由低频磁损和高频磁损组成,低频磁损主要与电流值有关,并且受开关频率的影响较小,高频磁损随开关频率的增加而减小,铜损主要受趋肤效应影响,开关频率越高,铜损越大.
1.2.2 变频器损耗与调制比的关系
从表1可以看出,功率器件的导通损耗和开关损耗以及滤波电感的磁芯损耗和铜损与电流成正相关.当负载不变时,电流与电压呈正相关.因此,导通损耗、开关损耗、磁芯损耗和铜损与调制比呈正相关.
1.3 功率器件的结温
功率器件平均结温的公式[11]可表示为:
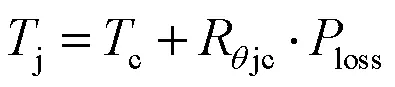
其中loss、jc、c和j分别是总损耗、功率器件的结壳热阻、功率器件的壳温度和结温.功率器件的总损耗包括开关损耗和导通损耗.功率器件的开关损耗与开关频率成正相关,而功率器件的导通损耗不受开关频率的影响.功率器件的开关损耗和导通损耗与调制比正相关.功率器件的结温与总损耗成正比,因此调制比和开关频率会影响功率器件的结温.
2 目标函数的选择
根据以上分析可知,输出电压的总谐波失真主要与每个谐波幅值有关,电压精度主要与电压的基波幅值有关,逆变器的效率与逆变器的总损耗呈负相关,而逆变器的结温由其损耗决定.电压的THD、电压精度和逆变器效率之间的相关性很小,因此有必要同时优化逆变器的三个指标.
为了优化输出电压的THD,可以将参考电压信号和输出电压的误差(电压误差)作为优化目标.当电压误差减小时,电压的基波分量接近额定电压,电压的谐波分量接近零,当电压精度提高时,电压谐波含量将减少.因此,可以在优化电压误差的同时,优化电压的THD和电压精度.
为了提高逆变器的效率并优化功率器件的结温,可以将逆变器的总损耗作为优化目标.随着逆变器损耗的降低,功率器件和滤波器的损耗也会降低,进而可提高逆变器的效率,降低功率器件的结温.为了便于分析,本文通过权重系数将多个优化目标组合为一个目标函数.目标函数的公式可写为:
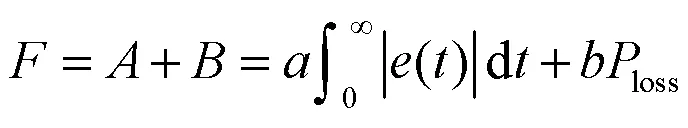
其中和分别是IAE函数部分和损耗部分,IAE中的()是电压误差,loss是逆变器的总损耗,和是目标函数的权重系数,且满足:
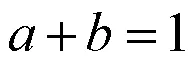
采用滞环控制器,开关频率不固定,功率器件的开关损耗和滤波电感的损耗将随着开关频率的变化而改变.因此,目标函数中损耗部分的权重系数应适当增加.
采用双闭环SPWM控制器,开关频率固定,可通过改变逆变器的调制比来改变逆变器的损耗.但是,当逆变器的输出电压质量满足一定条件(例如THD < 5%,输出电压精度为220 (1 ± 1.5%) V)时,双闭环控制参数对逆变器的损耗影响会很小,因此权重系数目标函数中损耗部分的比例需要适当降低.
3 单相逆变器的优化模型
本文将以粒子群优化算法对单相离网逆变器进行优化为例来验证本文提出的目标函数的有效性.优化模型见图2.优化模型由数字控制系统、主电路、目标函数和PSO算法组成.电压外环采用PI控制器,电流内环采用P控制器.目标函数的输入信号是电压误差()和逆变器的总损耗loss.需要优化包括电压回路的比例系数vp和积分系数vi以及电流回路的比例系数ip在内的参数.控制参数的更新过程如下:首先,PSO算法通过目标函数获得适应值;然后,通过评估适应值的大小来更新当前控制参数(适应值较小的控制参数替换适应值较大的控制参数);最后,大多数控制参数将保持接近全局最佳区域(逆变器的出色性能区域);PSO算法的公式[12]如下:
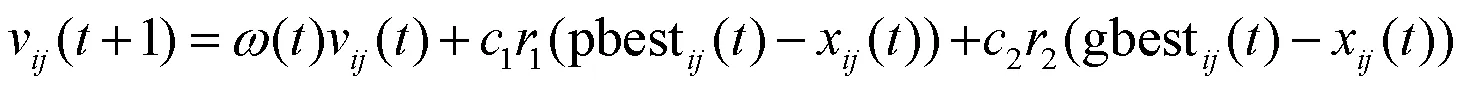
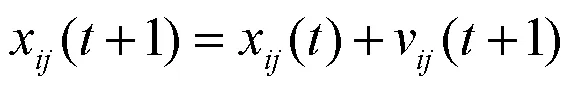
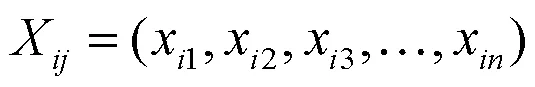
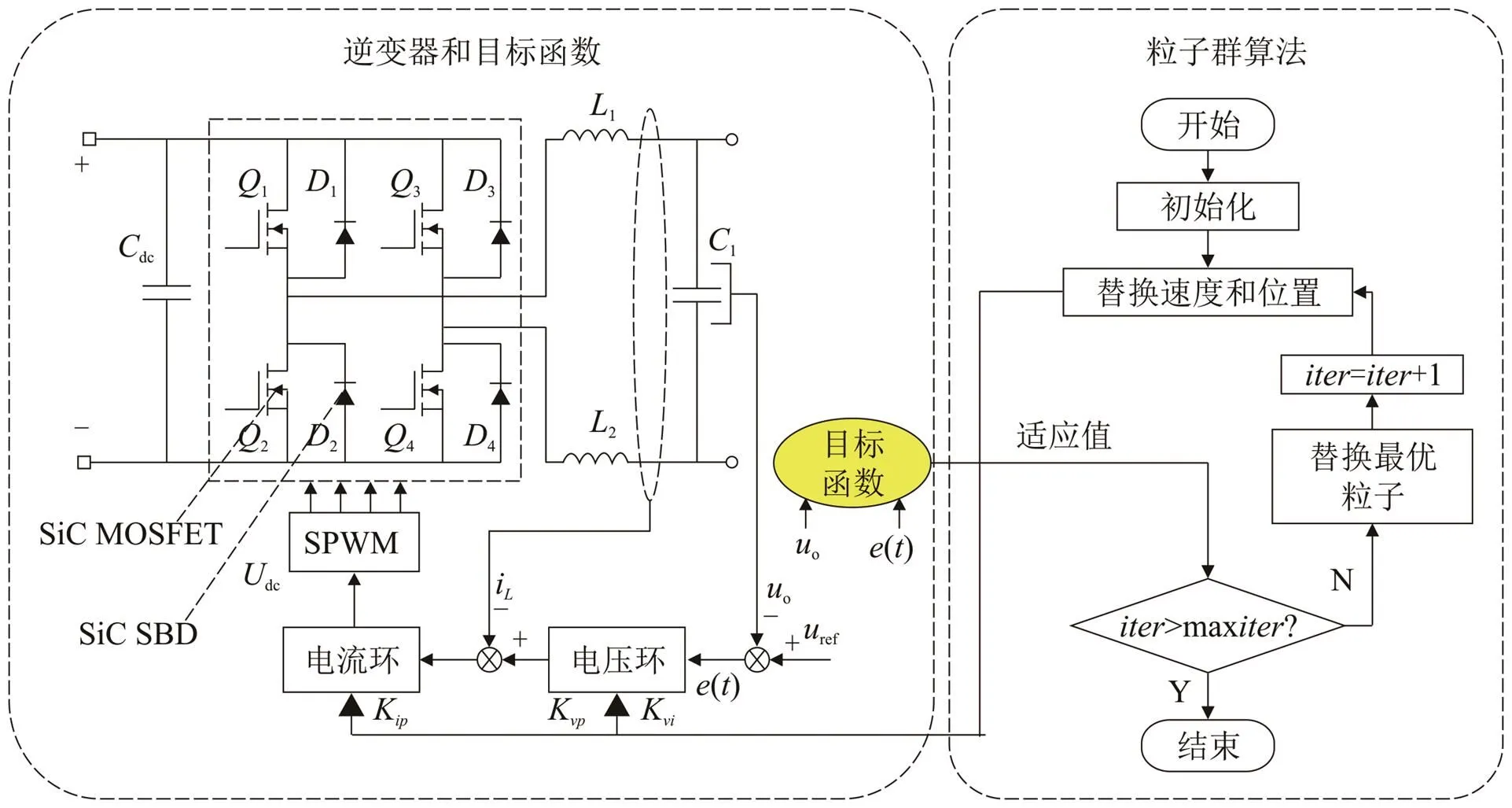
图2 优化模型
4 实验验证
为了验证优化后的目标函数在单相逆变器中的可行性和有效性,设置两组不同目标函数的实验对比,一组以电压谐波含量作为目标函数,另一组采用优化后的目标函数.实验装置中采用美国TI公司的DSP TMS320F28335进行数字运算.
实验平台如图3所示.实验条件和相关参数设置如下:功率器件采用1200V/24A SiC MOSFET (C2M0080120D) 和1200V/24A SiC SBD(C4D15120D);输入直流电压为400 V,输出交流电压的幅值为220 V,输出额定功率为2 kW,负载为24 Ω,开关频率为60 kHz,滤波电感为0.4 mH,滤波电容为7 uF;粒子群优化算法的加速因子1和2为2,目标函数中的权重系数和分别为0.9和0.1.为了便于分析,将仅考虑电压THD的目标函数设置为A组,将优化后的目标函数设置为B组.实验结果如表2、图4和图5所示.
表2给出了两组不同目标函数的比较结果,图4给出了比较结果的输出电压和电流波形.由结果可知,B组的输出电压的总谐波失真比A组的稍差,但其效率提高了0.227%,电压精度提高了0.88%.因此,采用优化后的目标函数,虽增大了输出电压的THD,但可使控制的精度更高,同时也可使逆变器的效率更高.

图3 实验平台

表2 结果比较
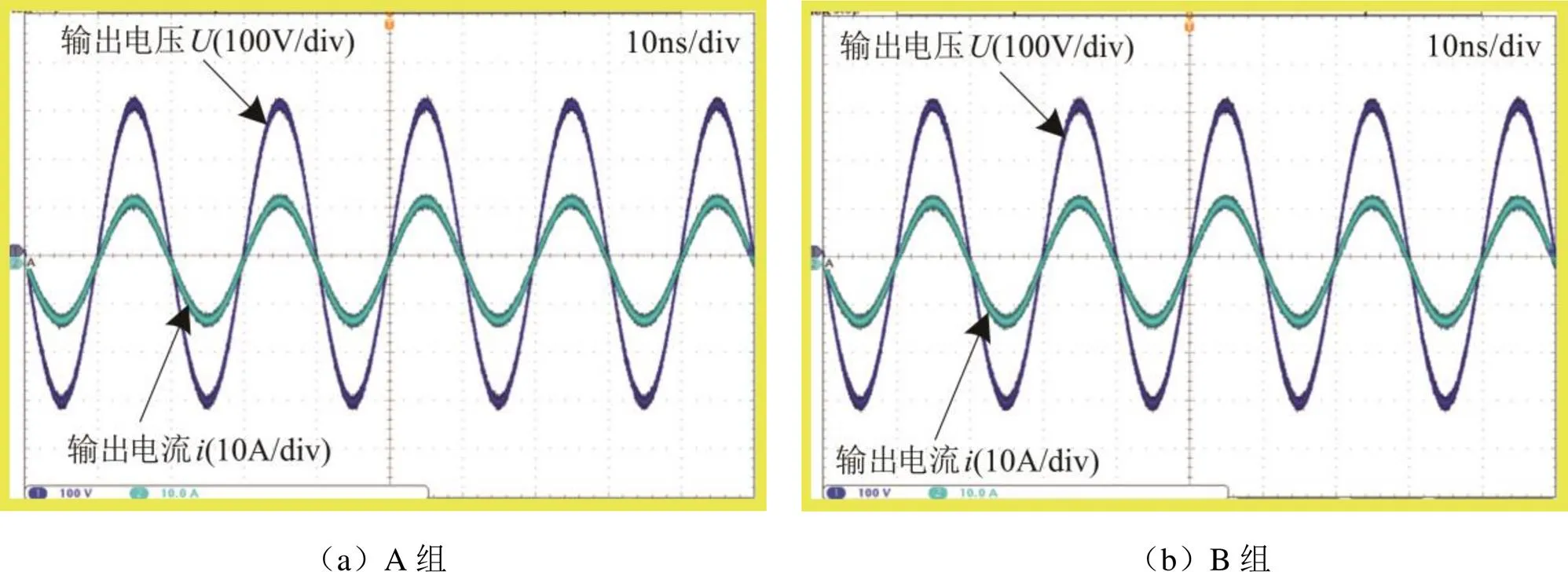
图4 输出电压和电流波形
图5是使用FLIR A655sc红外成像仪测量的功率器件的外壳温度图,A组功率器件的最高壳体温度为56.7℃,而B组功率器件的最高壳体温度为55.3℃.根据实验结果可知,采用优化后的目标函数,功率器件具有更低的结温.
以上实验结果表明,相较于仅考虑电压谐波含量的目标函数,采用优化后的目标函数,逆变器的整体性能更好.
5 结 论
本文提出了一种可以反映逆变器多个性能指标的目标函数,该目标函数由IAE函数和损耗函数组成,可以反映电压精度、电压的总谐波失真、逆变器的效率以及功率器件的结温等性能.以单相离网逆变器为例,通过PSO算法验证了该方法的可行性.实验结果表明,采用优化后的目标函数,逆变器的整体性能更好.因此,通过建立目标函数,智能算法可以更全面地提高逆变器的整体性能.当优化对象是电动机驱动器或并网逆变器时,需要修改目标函数中IAE部分的输入信号,可以将其修改为速度误差信号、当前误差信号或其他不同的误差信号.

图5 功率设备的红外图像
[1] Balasubramonian M, Rajamani V. Design and Real-time Implementation of SHEPWM in Single-phase Inverter Using Generalized Hopfield Neural Network [J]. IEEE Transactions on Industrial Electronics, 2014, 61(11): 6327-6336.
[2] Ahmadi D, Zou K, Li C, et al. A Universal Selective Harmonic Elimination Method for High-power Inverters [J]. IEEE Transactions on Power Electronics, 2011, 26(10): 2743-2752.
[3] Zhang K, Shan Z, Jatskevich J. Large- and Small-signal Average-value Modeling of Dual-active-bridge DC-DC Converter Considering Power Losses [J]. IEEE Transactions on Power Electronics, 2017, 32(3): 1964-1974.
[4] 郝鹏杰, 李云鹏, 李聪, 等. 集中式逆变器直流侧并联协调控制策略[J]. 石家庄铁道大学学报(自然科学版), 2020, 33(3): 65-71.
[5] 陈宝刚. 基于LCL滤波的单相光伏并网/离网逆变器控制策略的研究[D].重庆: 重庆理工大学, 2018: 11-15.
[6] Xiong Y, Sun S, Jia H, et al. New Physical Insights on Power MOSFET Switching Losses [J]. IEEE Transactions on Power Electronics, 2009, 24(2): 525-531.
[7] Glitz E S, Ordonez M. MOSFET Power Loss Estimation in LLC Resonant Converters: Time Interval Analysis [J]. IEEE Transactions on Power Electronics, 2019, 34(12): 11964-11980.
[8] Yamashita N, Murakami N, Yachi T. Conduction Power Loss in MOSFET Synchronous Rectifier with Parallel-connected Schottky Barrier Diode [J]. IEEE Transactions on Power Electronics, 1998, 13(4): 667-673.
[9] Reinert J, Brockmeyer A, De Doncker R W A A. Calculation of Losses in Ferro- and Ferrimagnetic Materials Based on the Modified Steinmetz Equation [J]. IEEE Transactions on Industry Applications, 2001, 37(4): 1055-1061.
[10] Cree.C2M0080120D Silicon Carbide Power MOSFET C2M TM MOSFET Technology [EB/OL]. [2020-02-04].https://www.wolfspeed.com/1200v-silicon-carbide-mosfets.
[11] Wang J, Li Z, Jiang X, et al. Gate Control Optimization of Si/SiC Hybrid Switch for Junction Temperature Balance and Power Loss Reduction [J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1744-1754.
[12] Peng Z, Wang J, Bi D, et al. The Application of Microgrids Based on Droop Control with Coupling Compensation and Inertia [J]. IEEE Transactions on Sustainable Energy, 2018, 9(3): 1157-1168.
Optimization Control of Objective Function of Single-phase Inverter
YE Zhonghao1, DAI Yuxing1, PENG Zishun2
(1. College of Electrical and Electronic Engineering, Wenzhou University, Wenzhou, China 325035;2. College of Electrical and Information Engineering, Hunan University, Changsha, China 410082)
The objective function is the assessment criteria for the intelligence algorithms to optimize the performance of the inverter. Aiming at the problems that the objective function of the inverter is not comprehensively considered and the overall performance of the inverter needs to be improved, an objective function that can reflect the multiple performance indicators of the inverter is proposed in this paper,which helps to improve the overall performance of the inverter through the intelligence algorithms. The proposed objective function can reflect the voltage accuracy, the total harmonic distortion (THD) of the voltage, the efficiency of the inverter, as well as the junction temperature performance of the power device. Its feasibility is verified through the single-phase off-grid inverter optimized by the particle swarm optimization algorithm.
Objective Function; Inverter; Loss Analysis; Junction Temperature
TM464
A
1674-3563(2022)01-0043-08
10.3875/j.issn.1674-3563.2022.01.006
本文的PDF文件可以从www.wzu.edu.cn/wzdxxb.htm获得
2021-03-02
湖南省重点领域研发计划项目(2019WK2012)
叶中豪(1995―),男,浙江温州人,硕士研究生,研究方向:电力电子与电力传动
(编辑:王一芳)
(英文审校:黄璐)

