三维MHD方程轴对称弱解的正则准则

陈芳如

三维MHD方程轴对称弱解的正则准则

陈芳如

(温州大学数理学院，浙江温州 325035)

MHD方程组；正则性准则；轴对称；Besov空间

本文考虑的三维粘性不可压缩磁流体动力学方程（Magnetohydrodynamics，MHD）形式如下：

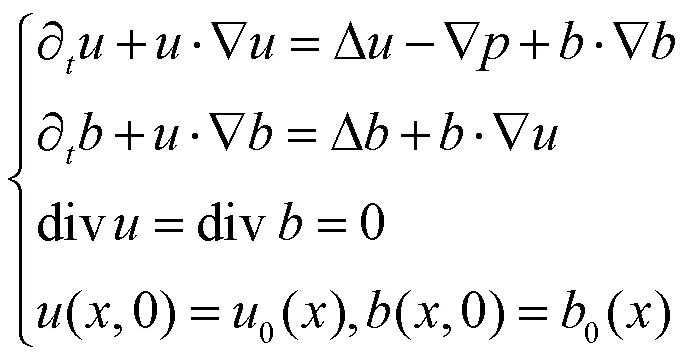
He等人在文献[1]中仅根据速度场建立了基本的Serrin型规律性准则，准确地说，表明了速度场若满足

或

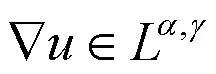
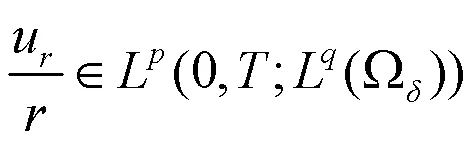
得到方程组（1）的弱解是光滑的．

得到方程组（1）的弱解是光滑的．同时，也有轴对称Navier-Stokes方程的分量正则性准则，如文献[10]，正则性准则只作用于涡场的两个分量．受Navier-Stokes方程结果的启发，我们将注意力转向轴对称MHD方程．Liu等人在文献[11]中构造了具有特定形式磁场的三维不可压缩MHD方程的一类轴对称解的正则性判据．

1 预备知识

2 定理及其证明

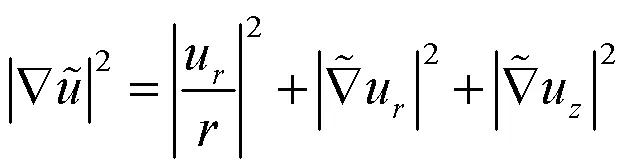
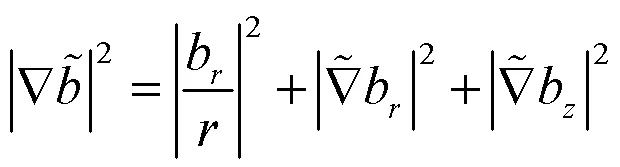
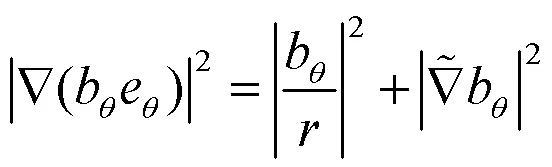
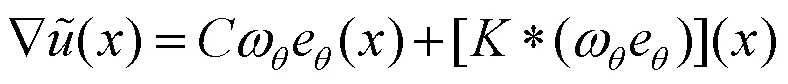
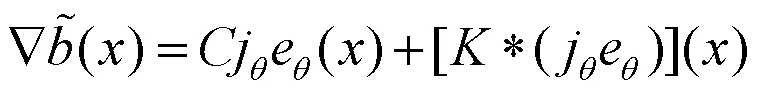
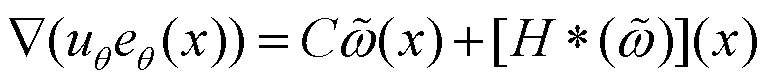
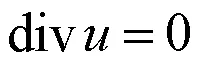
定理1的证明．

首先对（1）式进行先验估计．更准确地说，我们将展示下面的一个先验估计．

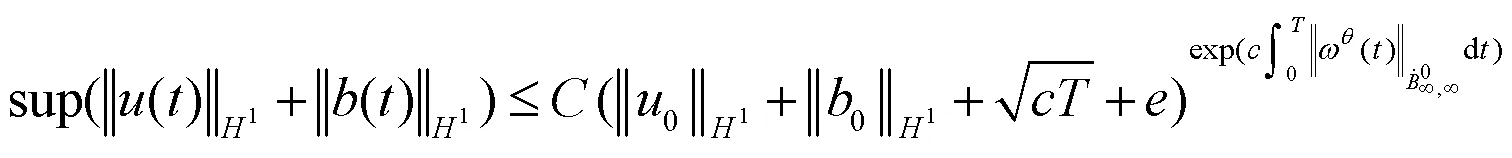
在（1）式上求其旋度，得到：

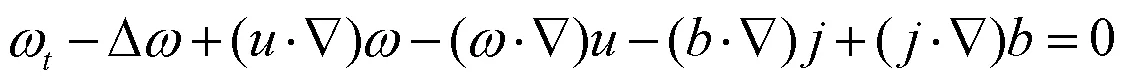
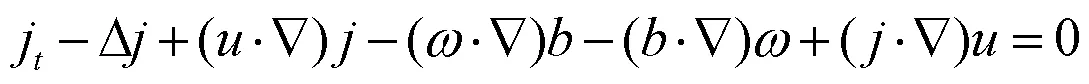
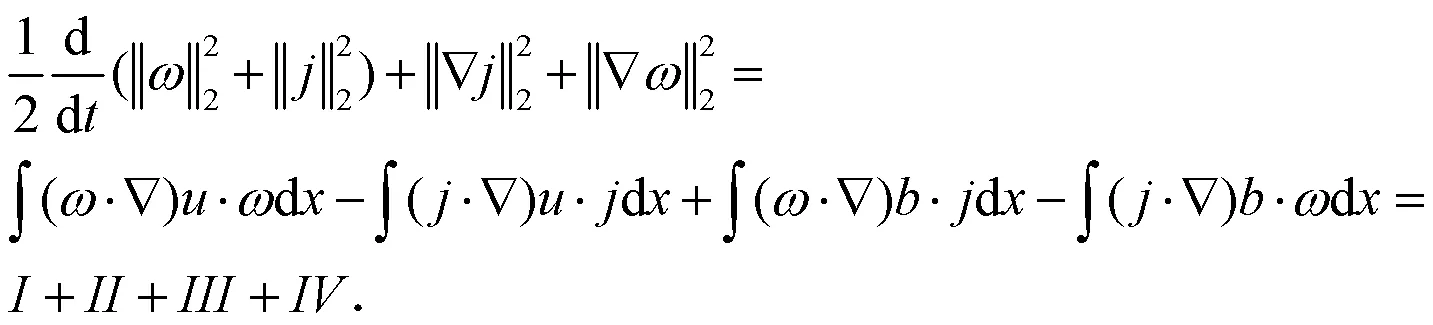
（17）式右侧第一项可估计为：

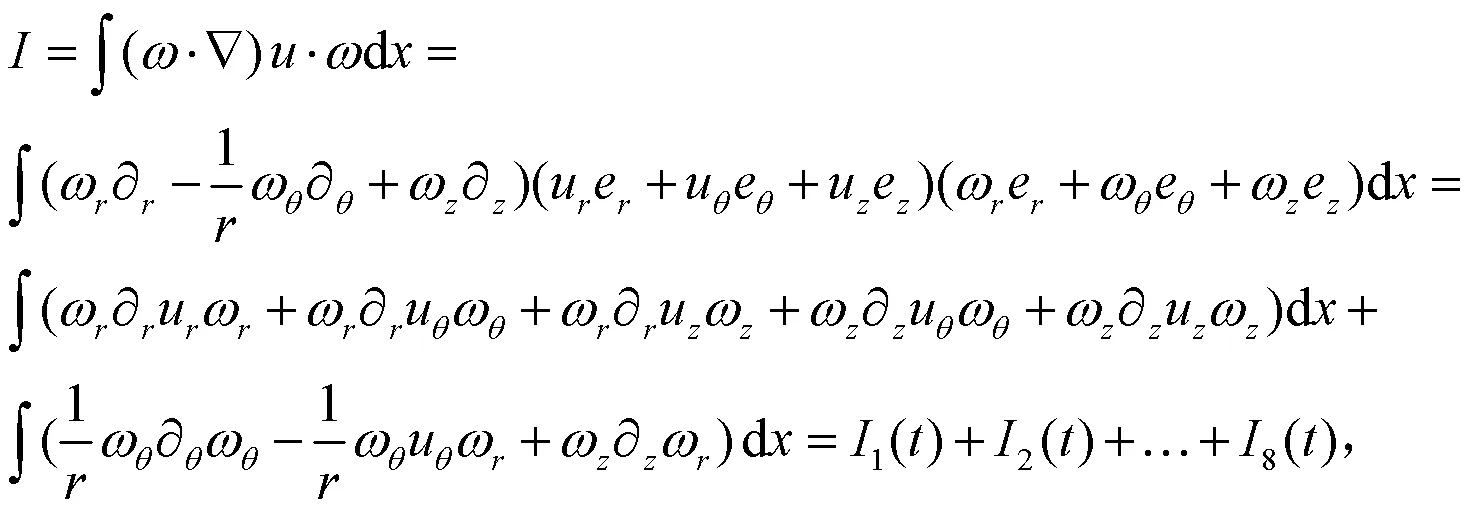
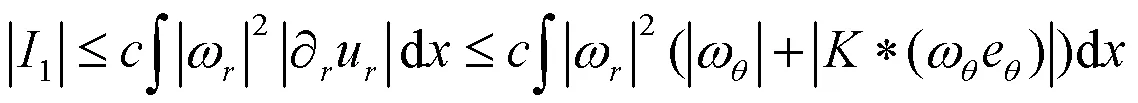
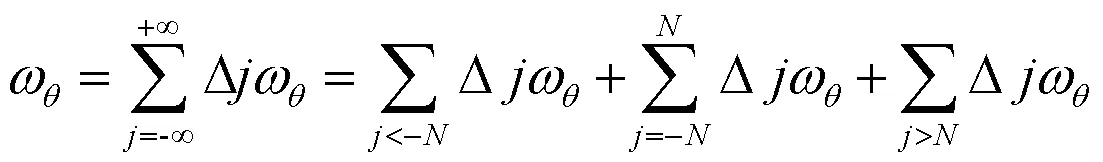
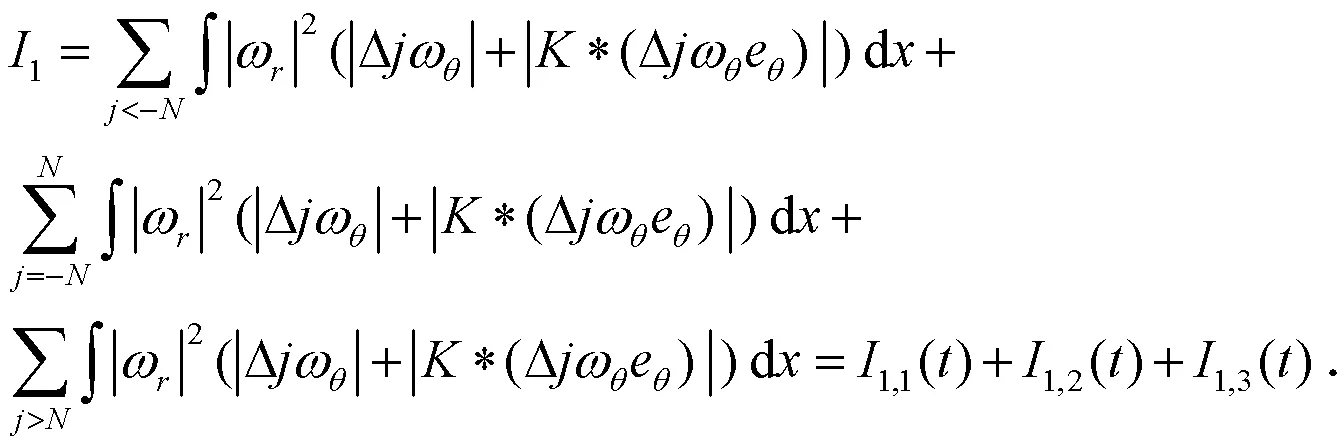
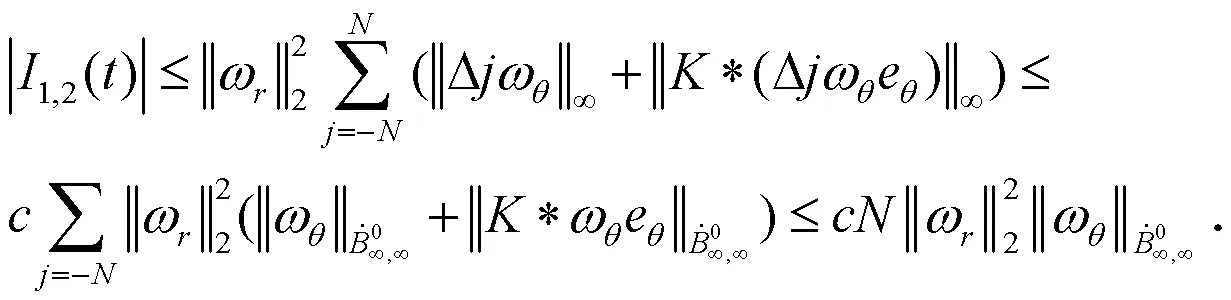
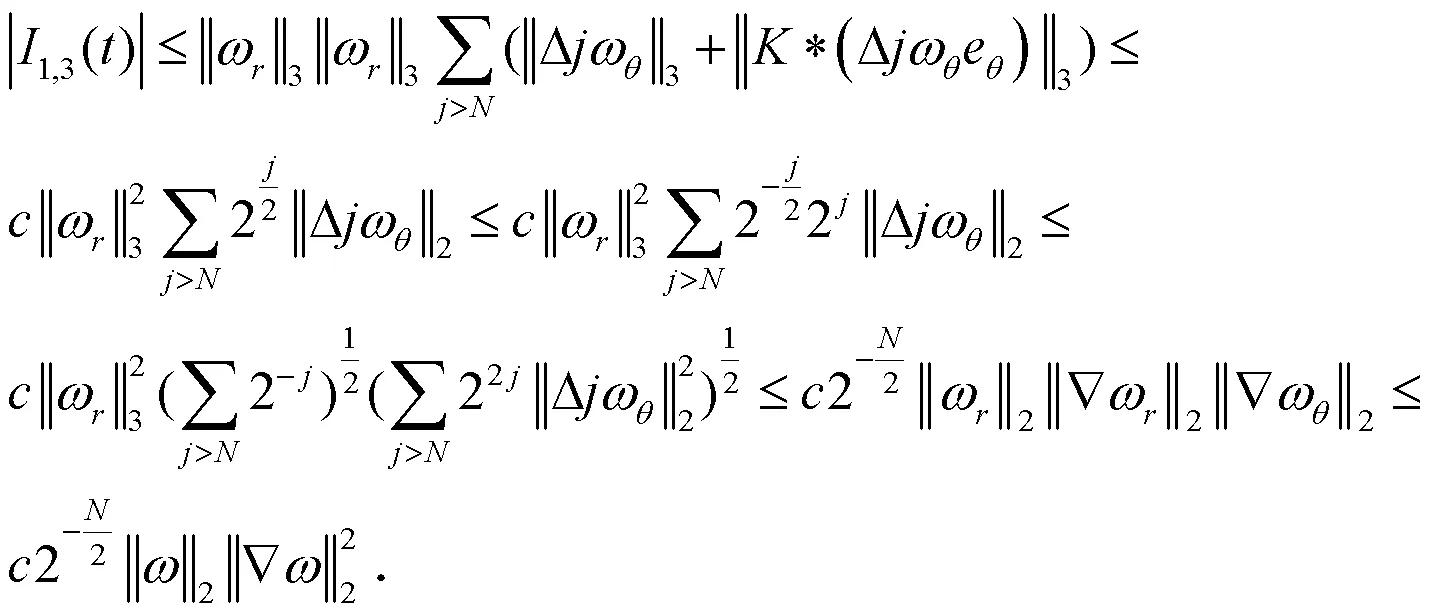
将（20）式―（22）式加起来，可得：

同样地，有以下估计

由此可得：

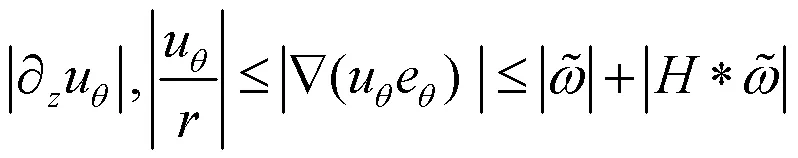
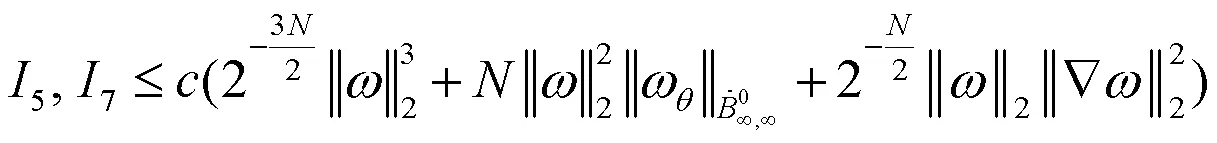
然后将（23）式、（24）式和（25）式代入（18）式，就得到了

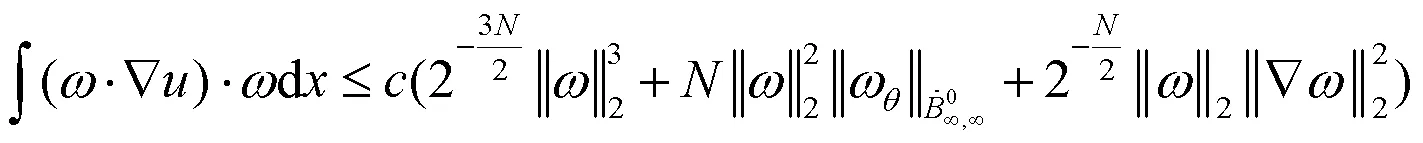
现在估计（17）式右边的第二项，

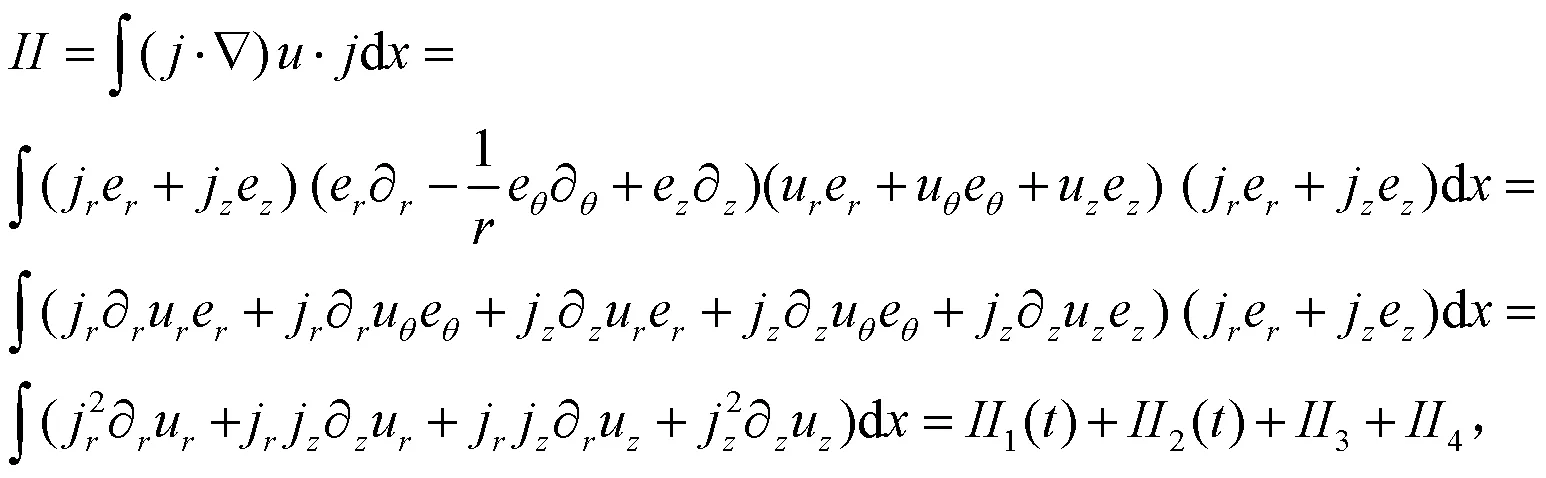
得到：

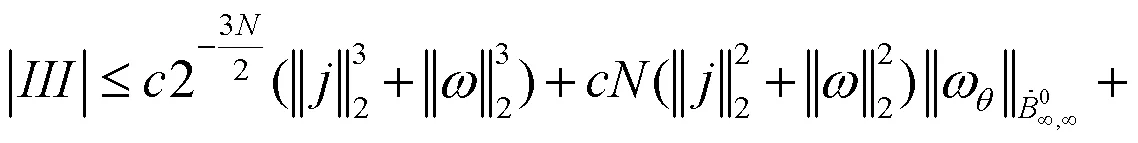
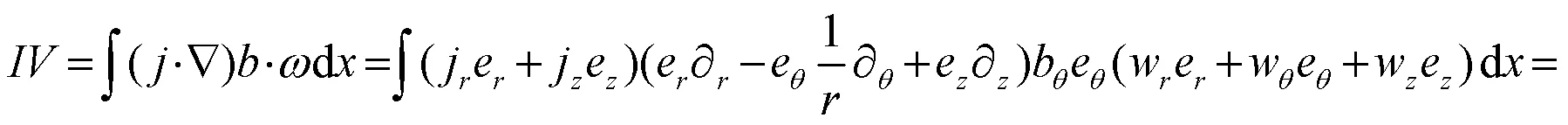
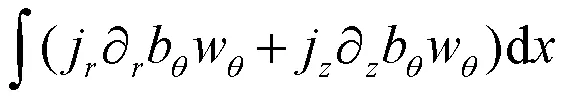
它遵循类似的方法，

组合（17）式、（26）式、（27）式、（28）式得到：

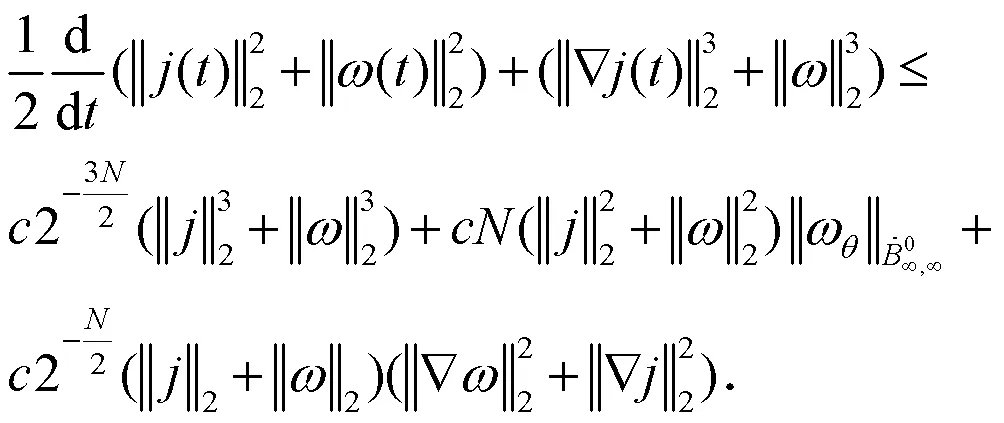
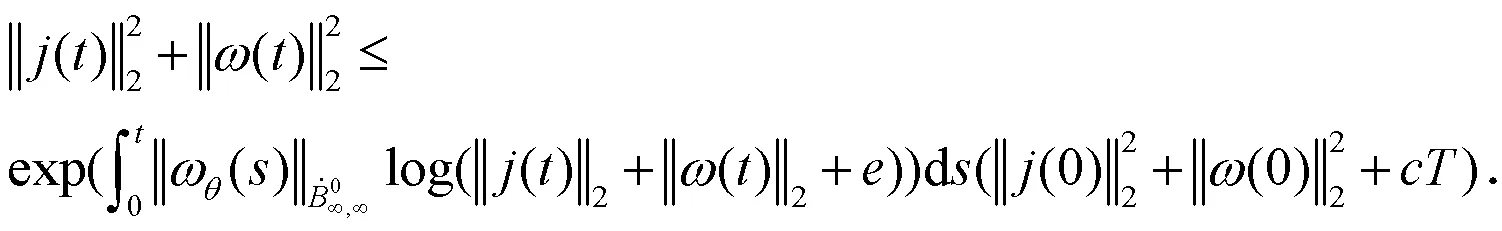
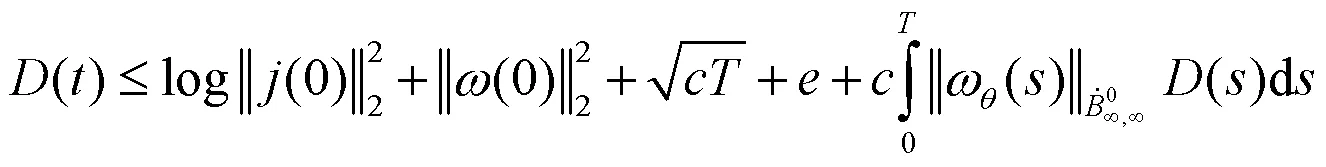
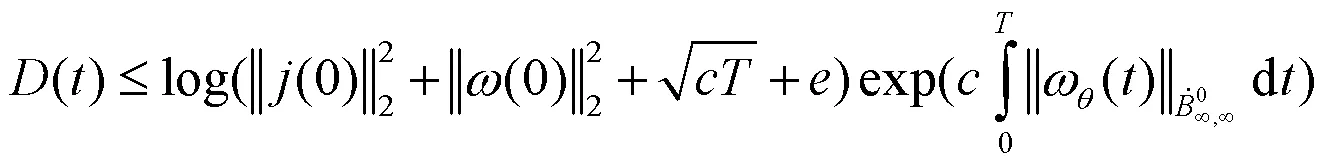
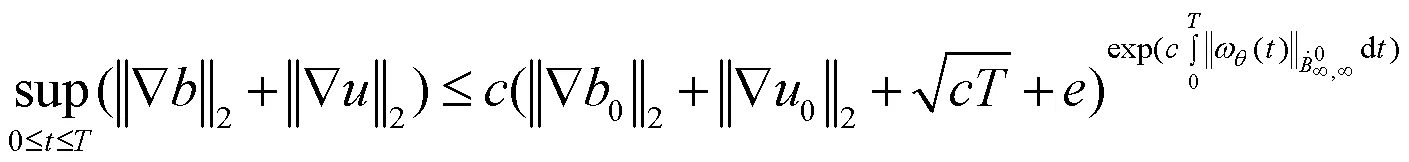
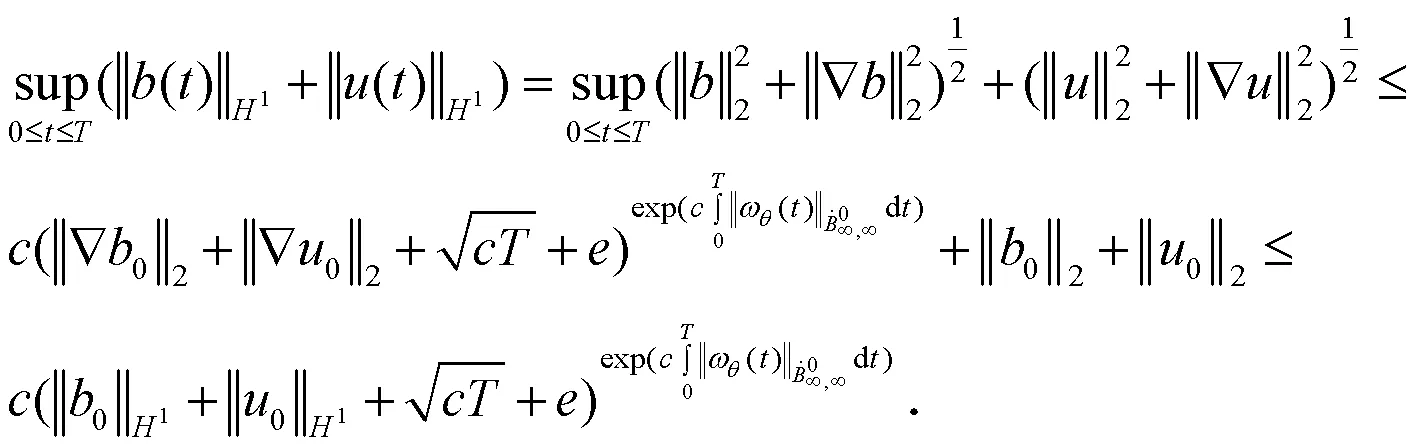
同样地，得到

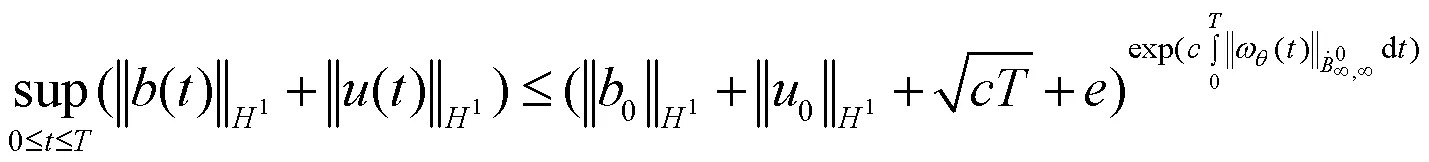
证明完成．

[1] He C, Xin Z. On the Regularity of Solutions to the Magnetohydrodynamic Equations[J]. Journal Differential Equations, 2005, 213(2): 235-254.

[2] Zhou Y. Remarks on Regularities for the 3D MHD Equations, Discrete Contin [J]. Journal of Dynamic Systems Measurement and Control-Transactions of the Asme, 2005, 12: 881-886.

[3] Chen Q, Miao C, Zhang Z. On the Regularity Criterion of Weak Solution for the 3D Viscous Magneto-hydrodynamics Equations, Commun [J].Communications in Mathematical Physics, 2008, 284: 919-930.

[4] Wu J. Bounds and New Approaches for the 3D MHD Equations [J]. Journal of Nonlinear Science, 2002, 12: 395-413.

[5] Wu J. Regularity Results for Weak Solutions of the 3D MHD Equations, Discrete Contin [J]. Journal of Dynamic Systems Measurement and Control-Transactions of the Asme, 2004,10: 543-556.

[6] Gala S, Guo Z, Ragusa M. A Regularity Criterion for the Three-dimensional MHD Equations in Terms of One Directional Derivative of the Pressure [J]. Computers and Mathematics with Applications, 2015, 70(12): 3057-3061.

[7] Tong D, Wang W. Conditional Regularity for the 3D MHD Equations in the Critical Besov Space [J]. Applied Mathematics Letters, 2020, 102: 106119.

[8] Chae D, Choe J. Regularity of solutions to the Navier-Stokes Equations [J]. Electronic Journal of Differential Equations, 1999, 56: 1-7.

[9] Kozono H, Ogawa T, Taniuchi Y. The Critical Sobolev Inequalities in Besov Spaces and Regularity Criterion to Some Semi-linear Evolutions [J]. Mathematische Zeitschrift, 2002, 242: 251-278.

[10] Chae D, Lee J. On the Regularity of the Axisymmetric Solutions of the Navier-Stokes Equations [J]. Mathematische Zeitschrift, 2002, 239: 645-671.

[11] Liu J. On Regularity Criterion to the 3D Axisymmetric Incompressible MHD Equations [J]. Mathematical Methods in the Applied Sciences, 2016, 39: 4535-4544.

[12] Stein E M. Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Interals [M]. Princeton: Princeton University Press, 1993:285-288.

Regularity Criteria of Axisymmetric Weak Solutions to the 3D MHD Equations

CHEN Fangru

(College of Mathematics and Physics, Wenzhou University, Wenzhou, China 325035)

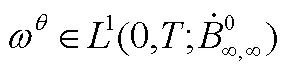
MHD Equations; Regularity Criteria; Axisymmetric; Besov Space

O175

A

1674-3563(2022)01-0025-09

10.3875/j.issn.1674-3563.2022.01.004

本文的PDF文件可以从www.wzu.edu.cn/wzdxxb.htm获得

2020-10-21

陈芳如(1995― )，甘肃定西人，硕士研究生，研究方向：微分方程与动力系统

(编辑：王一芳)

(英文审校：黄璐)