模糊蕴涵生成的序

李 琪,孙文璟,张丽珠,薄其高,李 钢

齐鲁工业大学(山东省科学院) 数学与统计学院,山东 济南 250353

模糊蕴涵由于在近似推理、模糊控制、模糊关系方程、模糊形态学、图像处理等领域[1-9]的广泛应用,逐渐引起了学者们的关注。文献[1]讨论了模糊蕴涵的性质,文献[10]分析了模糊蕴涵诱导的偏序,文献[11]研究了相关的方程。在一般情况下,由于单位区间是一个有界格,类似在其他逻辑运算符的情况下,因此学者们在有界格上生成蕴涵并研究生成的蕴涵与其他逻辑算子之间的关系[12-14]。在本文中,我们在有界格L上定义了一种由蕴涵生成的新偏序I。另外,给出由合取一致模U生成的偏序≤U,并探讨两个序之间的关系。

1 预备知识

本节中,我们回顾本文使用的一些基本概念和结论。

定义1[13]:设(L,≤,0,1)是一个有界格。若二元函数T(S),满足交换性、结合性、单调递增且具有单位元1(0),则称之为三角模(三角余模)。

定义2[14]:设(L,≤,0,1)是一个有界格。若二元函数U:L2→L是交换的,结合的,非递减的,且存在e∈L使得U(e,x)=x,x∈[0,1]成立,则称U为定义在L上的一致模,e为单位元。

显然,三角模(三角余模)是一致模e=1(e=0)的特殊情况。另外,U(0,1)∈{0,1}。若U(0,1)=0,称U为合取一致模；若U(0,1)=1,称U为析取一致模。

在本文中,符号U(e)表示有界格L上关于单位元e∈L的一致模集合。

定义3[15]:设L≠∅。若对于任意的a,b,c∈L,二元关系≤,满足以下性质:

a≤a； (自反性)

若a≤b且b≤a,那么a=b； (反对称性)

若a≤b且b≤c,那么a≤c； (传递性)

则称≤为L上的偏序。

定义4[11]:设(L,≤,0,1)是一个有界格。若一元递减函数N:L→L满足N(0)=1,N(1)=0,则称N为模糊否定。进一步:如果L上的N是对合(N(N(x))=x,x∈L)的,那么称N为强否定。

定义5[12]:有界格(L,≤,0,1)上的二元函数I:L2→L,对于任意的x,y,z∈[0,1]满足以下条件:

当x≤y时,I(x,z)≥I(y,z)成立；

(I1)

当y≤z时,I(x,y)≤I(x,z)成立；

(I2)

I(1,0)=0,I(0,0)=I(1,1)=1；

(I3)

则称I为模糊蕴涵。

定义6[1,3,5]:若对于任意的x,y,z∈[0,1],在有界格L上的蕴涵I关于合取一致模U的单位元e满足输入法则

I(x,I(y,z))=I(U(x,y),z)。 (LIU)

若对于任意的y∈L,蕴涵I关于e满足左中性原则

I(e,y)=y,e∈]0,1[,y∈[0,1]。 (NPe)

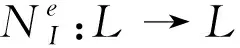
为I关于e的自然否定。

定义7[1]:

1)由析取一致模Ud和强否定N生成的(U,N)-蕴涵如下所示:

IUd,N(x,y)=Ud(N(x),y),x,y∈L。 (1)

2)由析取一致模Ud,合取一致模U和强否定N生成的QL-算子如下所示:

IQL(x,y)=Ud(N*(x),U(x,y)),x,y∈L。 (2)

若IQL是模糊蕴涵,那么对于任意的x∈L,Ud一定是使得Ud(x,N(x))=1的三角余模。在这种情况下,IQL称为QL-蕴涵。

3)设f:[0,1]→[0,∞]为严格递减且连续的函数有f(1)=0。函数If:[0,1]×[0,1]→[0,1]定义如下:

If(x,y)=f-1(x·f(y)),x,y∈[0,1], (3)

称为f-生成蕴涵,约定0·∞=0。

4)设g:[0,1]→[0,∞]为严格递增且连续的函数有g(0)=0。函数Ig:[0,1]×[0,1]→[0,1]定义如下:

5)设h:[0,1]→[-∞,∞]为严格递减且连续的函数有h(0)=-∞,h(e)=0和h(1)=+∞。函数Ih:[0,1]×[0,1]→[0,1]定义如下:

称为h-蕴涵。

6)设h:[0,1]→[0,1],当e∈]0,1[时为严格递减且连续的函数有h(e)=0。函数I:[0,1]×[0,1]→[0,1]定义如下:

称为广义h-蕴涵。其中函数h(-1)是h的伪逆,如下所示:

此外,广义h-蕴涵可以用h(-1)简化为如下:

2 主要结论

在本节中,通过模糊蕴涵和一致模分别定义了两种偏序,并讨论了这些序相关的性质。进一步研究了二者之间的关系。

引理1:设(L,≤,0,1)是一个有界格且U∈U(e)。序关系≤U定义如下,对于x,y∈L,

x≤Uy⟺∃l*≥e使得U(l*,y)=x, (10)

是一个偏序。

证明:我们将从自反性,反对称性和传递性来证明≤U是一个偏序。

(自反性)若我们取l*=e≥e,那么对于任意的x∈L,由U(e,x)=x,得x≤Ux。

(反对称性)设x,y∈L使得x≤Uy且y≤Ux。那么存在l1,l2≥e使得U(l1,y)=x,U(l2,x)=y。因此我们得到x=U(l1,y)≥U(e,y)=y,y=U(l2,x)≥U(e,x)=x,则x=y。

(传递性)对于任意的x,y,z∈L,设x≤Uy且y≤Uz。那么存在两个元素l1,l2≥e使得U(l1,y)=x,U(l2,z)=y。通过x=U(l1,y)=U(l1,U(l2,z))=U(U(l1,l2),z)和U(l1,l2)≥e,得到x≤Uz。

定义8:设(L,≤,0,1)是有界格,U∈U(e)为合取一致模且I是满足(LIU)的蕴涵。对于任意的x,y∈L,序关系定义如下:

xIy⟺∃l≥e使得I(l,x)=y。 (11)

注1:注意到,公式(10)定义的序≤U和文献[10]中的S-偏序是相互对偶的。简单地说,当e=0时,公式(11)定义的序S和文献[12]中的I-偏序是相互对偶的。

引理2:设(L,≤,0,1)是有界格,U∈U(e)为合取一致模且I是满足(LIU)的蕴涵。若I关于单位元e满足(NPe),那么公式(11)定义的序关系I为L上偏序。

证明:我们将从自反性,反对称性和传递性来证明。

(自反性)由(NPe)可知存在l=e≥e,使得对于任意的x∈L,有I(l,x)=I(e,x)=x。

(反对称性)设x,y∈L使得xIy并且yIx,那么存在l1,l2≥e,使得I(l1,x)=y,I(l2,y)=x。通过(I1)和(NPe),得x=I(e,x)≥I(l1,x)=y和y=I(e,x)≥I(l2,y)=x,因此x=y。

(传递性)对于任意的x,y,z∈L,设xIy且yIz。那么存在两个元素l1,l2≥e,使得I(l1,x)=y,I(l2,y)=z。通过(LIU)我们得到z=I(l2,y)=I(l2,I(l1,x))=I(U(l2,l1),x),则

U(l2,l1)=U(l1,l2)≥U(e,e)=e。

那么xIz。

进一步,下面的引理将证明公式(11)中定义的偏序与自然序的关系。

引理3:设(L,≤,0,1)是有界格,U∈U(e)为合取一致模且I是满足(LIU)与(NPe)的蕴涵。若对于任意的x,y∈L有(x,y)∈I,那么(y,x)∈≤。

证明:对于任意的x,y∈L,设xIy。那么,存在元素l≥e使得I(l,x)=y。

通过(11)和(NPe),我们得到x=I(e,x)≥I(l,x)=y。所以,(y,x)∈≤。

引理4:设(L,≤,0,1)是有界格并且U∈U(e)。若对于任意的x,y∈L,有(x,y)∈≤U,那么(y,x)∈≤。

证明:对于任意的x,y∈L,设x≤Uy。那么存在l≥e使得U(l,y)=x。

我们得到y=U(e,y)≤U(l,y)=x。所以,(y,x)∈≤。

引理3和引理4的逆不一定成立,下面给出了一个反例。

例1:设一致模ULK=(TLK,SLK,0.5)∈Umin。那么由ULK生成的RU-蕴涵如下所示:

得出矛盾。

引理5:设(L,≤,0,1)是有界格,U∈U(e)为合取一致模且I:L2→L是满足(LIU)和(NPe)的蕴涵。对于任意的x,y,z∈L,

xIy⟹I(z,x)II(z,y)。 (13)

证明:对于任意的x,y∈L,设xIy。那么存在l≥e使得I(l,x)=y。

通过(LIU),得到下列等式:

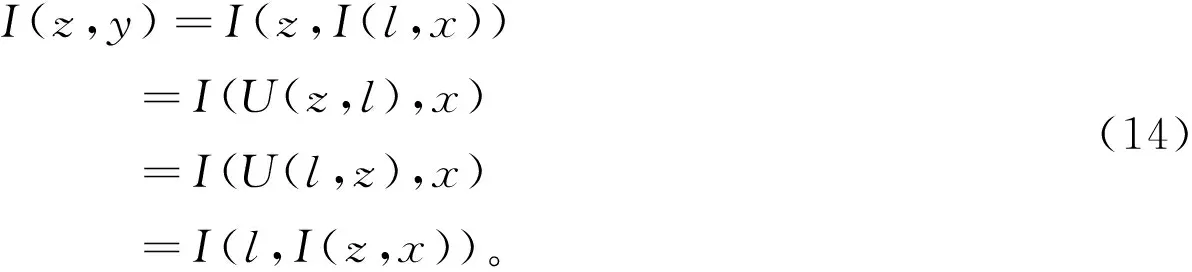
那么,由I(z,y)=I(l,I(z,x))和l≥e得I(z,x)II(z,y)。

由文献[16]的命题7可知,(L,Iφ)是一个偏序集。下面的引理讨论序I和Iφ之间的关系。

引理6:设(L,≤,0,1)是有界格,U∈U(e)为合取一致模且I:L2→L是满足(LIU)和(NPe)的蕴涵。设φ:L→L是满足φ(e)=e的保序双射,那么对于任意的x,y∈L,当且仅当φ(x)Iφ(y)时,xIφy。

证明:(充分性)对于任意的x,y∈L,设xIφy。那么存在元素l≥e使得Iφ(l,x)=y。

由于φ-1(I(φ(l),φ(x)))=y,因此,得到I(φ(l),φ(x))=φ(y)。此外,φ(l)≥φ(e)=e是显然的。则φ(x)Iφ(y)。

(必要性)设φ(x)Iφ(y),那么存在元素l≥e使得I(l,φ(x))=φ(y)。由于φ是双射的,对于l∈L,存在元素l*∈L使得φ(l*)=l。由于φ是保序双射并且l≥e,则l*≥e是显然的。由φ(y)=I(l,φ(x))=I(φ(l*),φ(a)),我们得到Iφ(l*,x)=φ-1(I(φ(l*),φ(x)))=y,其中l*≥e。则xIφy。

引理7:设(L,≤,0,1)是有界格,U∈U(e)为合取一致模且I:L2→L是满足(LIU)和(NPe)的蕴涵。设φ:L→L是满足φ(e)=e的保序双射。那么,对于任意的x,y∈L,当且仅当(L,I)是一个格,(L,Iφ)是一个格。

证明:本引理证明过程与文献[16]的定理2类似。

下面,我们证明序≤U与文献[10]中定义的序U是不同的。此外,讨论了由g-,f-生成蕴涵,h-蕴涵生成的序I与U生成的序≤U之间的关系,序I关于合取一致模的单位元e满足输入法则(LIU)和左中性原则(NPe)。

下面的引理给出了公式(10)定义的序≤U与文献[10]中定义的序的区别。

引理8:设(L,≤,0,1)是有界格,U∈U(e)为合取一致模且I:L2→L是满足(LIU)和(NPe)的蕴涵。那么,对于任意的x,y,z∈L,

x≤Uy⟹I(y,z)II(x,z)。 (15)

证明:对于任意的x,y∈L,设x≤Uy。那么,存在元素l≥e使得U(l,y)=x。

由I(l,I(y,z))=I(U(l,y),z)=I(x,z)且l≥e,我们得到I(y,z)II(x,z)。

推论1:设(L,≤,0,1)是有界格,U∈U(e)为合取一致模,e∈[0,1[且I:L2→L是满足(LIU)和(NPe)的蕴涵有I(1,e)=0。那么,对于任意的x,y∈L,

引理9:设(L,≤,0,1)是有界格,U∈U(e)为合取一致模且I:L2→L是满足(LIU)和(NPe)的蕴涵。那么,对于任意的x,y∈[e,1],xUy⟹I(x,z)II(y,z),z∈L。

证明:对于任意的x,y∈[e,1],设xUy。那么,存在元素l≥e使得U(x,l)=y。

由I(l,I(x,z))=I(U(l,x),z)=I(y,z)且l≥e,我们得到I(x,z)II(y,z)。

由文献[11]的结果得到以下定理。

定理1:设(L,≤,0,1)是有界格,Ud为析取一致模,N为强否定且IUd,N是L上的结合(U,N)-蕴涵。那么,当且仅当Uc为L上的一致模且定义如下:

Uc(x,y)=N(Ud(N(x),N(y))),x,y∈L,

IUd,N关于合取一致模Uc满足输入法则(LIUc)。

引理10:设(L,≤,0,1)是有界格,Ud∈U(e)为析取一致模且N为L上的强否定。设IUd,N为关于合取一致模Uc满足输入法则(LIUc)的结合(U,N)-蕴涵。那么,对于任意的x,y∈L,当且仅当N(y)≤UCN(x)时,xIUd,Ny。

证明:通过定理1可得Uc是Ud的N-对偶。由于N是强否定,显然N是满射。那么对于任意的e∈L,存在元素e’使得N(e’)=e,可得

由此看来,元素e’∈L是Uc的单位元。因此,由引理2可知,(L,IUd,N)是一个偏序集。

(充分性)对于任意的x,y∈L,设xIUd,Ny。则存在元素l≥e’使得IUd,N=(l,x)=y,

其中Ud(N(l),x)=y。由于Uc是Ud的N-对偶,我们有

Uc(l,N(x))=N(Ud(N(l),N(N(x))))

=N(Ud(N(l),x)

=N(y)。

(18)

则N(y)≤UCN(x)。

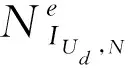
推论2:设(L,≤,0,1)是有界格,Ud∈U(e)为析取一致模且N为L上的强否定。设IUd,N为关于合取一致模Uc满足输入法则(LIUc)的结合(U,N)-蕴涵。那么,当且仅当(L,IUd,N)是一个格,(L,≤UC)是一个格。

由文献[11]的结论,得到下面定理。

定理2:设(L,≤,0,1)是有界格,x∈L。S为满足S(x,N(x))=1的三角余模,U为合取一致模并且N为L上的强否定。若相应的QL-算子关于合取一致模Uc满足输入法则(LIUc),则Uc和U均是L上的三角模。

通过定理2,我们得出以下结论。

推论3:设(L,≤,0,1)是有界格,IQL是由合取一致模U,析取一致模Ud和L上的强否定N*生成的QL-蕴涵。若IQL关于合取一致模Uc满足输入法则(LIUc),那么(L,IQL)是反链。

证明:IQL(x,y)=Ud(N*(x),U(x,y))是显然的。由于IQL是模糊蕴涵,Ud一定为满足Ud(x,N*(x))=1,x∈L的三角余模。所以,通过定理2的结论可知,Uc和U均是L上的三角模且Uc的单位元e一定是1。由于IQL(1,y)=Ud(N*(1),U(1,y))=Ud(0,y)=y,那么IQL关于1满足(NP)。则(L,IQL)是一个偏序集。由文献[1]的命题7.39可知,IQL为由IQL(x,y)=S(N*(x),y)定义的(S,N)-蕴涵,且Uc是S的N*-对偶。下面,设xIQLy,那么存在l=1使得y=IQL(1,x)=S(N*(1),x)=x。因此,(L,IQL)是反链。

推论4:设Ig:[0,1]×[0,1]→[0,1]是关于三角模T满足输入法则的g-生成蕴涵,那么([0,1],Ig)是反链。

证明:由文献[1]中的定理3.2.8已知Ig关于1满足左中性原则(NP)。因此,由引理2可知,([0,1],Ig)是一个偏序集。

对于任意的x,y∈[0,1],若xIgy,那么存在l=1使得x=Ig(1,x)=y。因此,([0,1],Ig)是反链。

相似地,下面的推论也成立。

推论5:设If:[0,1]×[0,1]→[0,1]是关于三角模T满足输入法则的f-生成蕴涵,那么([0,1],If)是反链。

推论6:设Ih:[0,1]×[0,1]→[0,1]是关于三角模T满足输入法则的(广义)h-蕴涵,那么([0,1],Ih)是反链。

3 结 论

本文介绍了一类序,它是由有界格上满足输入法则(LIU)和左中性原则(NPe)的蕴涵定义的序I,并讨论了相关性质。另外,给出基于有界格上一致模的一种新的序≤U。我们探讨了由关于合取一致模U的单位元e满足输入法则(LIU)和左中性原则(NPe)的(U,N)-蕴涵生成的序I与序≤U之间的关系。得到由QL-,g-,f-生成蕴涵,h-蕴涵生成的序I所构成的序结构(L,I)。结果表明,相应的序结构都是反链。