横向扫描敏感子弹的命中概率分析

刘璐伟，李 明，程晋伟，马宇腾，毛 亮

(北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081)

1 引言

智能地面封锁弹药可以在一定时间内，对指定区域实施封锁，从而为己方赢得时间，掌握战时主动权。其中，横向扫描敏感子弹是地面封锁弹药的智能作战单元，不仅可以打击地面车辆，还可以打击超低空飞行的直升机等敌方目标，具有响应速度快等优势，是目前的研究热点。

横向扫描敏感子弹的命中概率与稳态扫描特性密不可分。近年来，针对敏感子弹在不同弹道中的稳态扫描特性和识别命中概率开展了大量研究[1]。李臣明等[2]采用四元数法建立了末敏弹系统的稳态扫描阶段的运动方程，仿真证明了基于四元数法变换的弹道模型不会出现参数退化的情况，同时可提高运算速度和精度，比欧拉方程更适于描述末敏弹的姿态运动；赵博博等[3]通过分析掠飞末敏弹的扫描区域特性，推导求解了捕获概率的解析公式，并分析了弹丸瞄准点、初速、目标速度等因素对捕获概率的影响；于涛等[4]通过分析上升扫描式末敏子弹的作用过程，建立了毁伤效能评估模型，得到了毁伤效能随子弹初始扰动、转速、目标速度等因素的变化规律；于宁等[5]分析了一种智能地雷的亚音速和跨音速流场，得到了气动力因子随攻角增长的变化规律；杨永亮等[6]根据末敏子弹的非对称特点，推导了超大攻角下空间六自由度弹道方程，研究了弹体结构对扫描特性的影响规律。

本文首先分析横向扫描敏感子弹的作用原理和扫描特性，在耦合子弹摆动角的情况下，分别建立了子弹对车辆目标的捕获识别、起爆命中模型，采用蒙特卡洛法，求解了不同转速、弹目距离、识别阈值和目标速度等条件下的命中概率，并对影响子弹毁伤效能的因素进行了分析。

2 横向扫描敏感子弹飞行动力学方程

2.1 子弹结构及作用过程

横向扫描敏感子弹是一种新型结构的敏感弹药，由战斗部、敏感器、电子仓、整流罩等部件组成，其敏感装置和爆炸成型战斗部呈一定角度，横置于弹体内，弹体结构如图1所示。

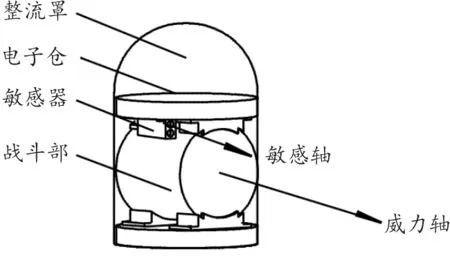
图1 敏感子弹结构示意图

横向扫描敏感子弹毁伤目标需要经过扫描识别、起爆命中2个阶段，分别将扫描识别出目标的概率定义为捕获率，将起爆命中目标的概率定义为命中率。敏感器轴线和战斗部轴线相对与目标尺寸很细小，可简化为一条直线，分别记为敏感轴和威力轴。当地面封锁弹药发现敌方目标并做出攻击指令后，横向扫描敏感子弹药垂直发射，并立即启动敏感装置，敏感轴在周围空间中形成自下而上的螺旋扫描线，子弹在周期性摆动和上升旋转中探测、识别并打击目标。其作用过程如图2所示。

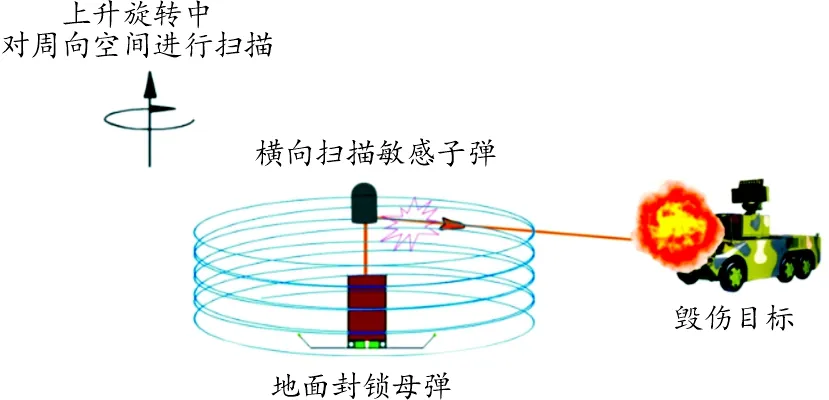
图2 敏感子弹作用过程示意图

2.2 子弹运动微分方程的建立

横向扫描敏感子弹的运动可分为质心运动和绕心运动。其质心运动只是沿铅锤轴方向运动，轨迹相对简单，故主要考虑弹体的绕心运动。选取坐标系如下：地面惯性坐标系，基准坐标系，弹体坐标系，使用俯仰角θ1、偏航角θ2、滚转角φ作为子弹转动的广义坐标，如图3所示，通过推导欧拉动力学方程，建立子弹绕心转动方程组为：

(1)

其中，

式(1)中:ωx1、ωy1、ωz1分别为子弹绕弹体坐标系x1轴、y1轴、z1轴转动的角速度；A、B、C分别为子弹对x1轴、y1轴、z1轴的惯性矩；D为子弹对x1z1平面的惯性积。

2.3 子弹摆动角的计算

定义摆动角η为威力轴与水平面的夹角，即O-y1轴与O-x0y0平面的夹角，O-y2是O-y1轴在O-x0y0平面内的投影，如图3所示。

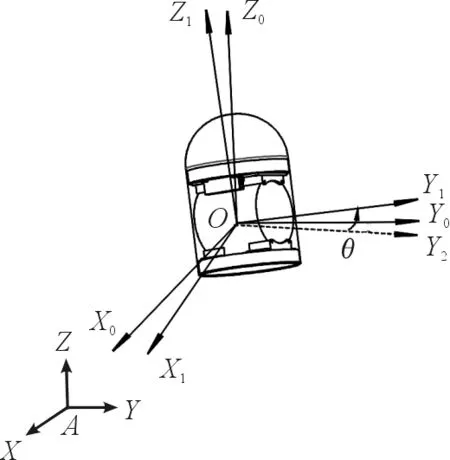
图3 坐标系示意图

理想情况下，O-y1轴与O-x0y0平面平行，但在实际中，弹轴存在摆动的情况，摆动角η随子弹运动呈周期性变化，如图4所示。由O-y1轴在基准坐标系中的方向余弦可知，摆动角η表达式为：

(2)

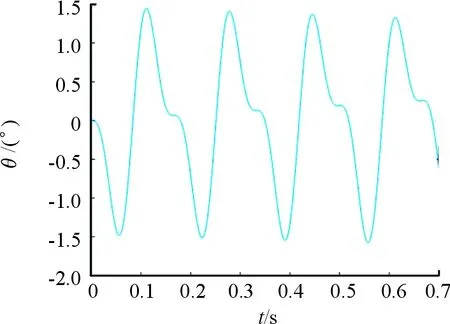
图4 摆动角随时间变化的曲线

3 横向扫描敏感子弹命中概率模型

3.1 命中概率影响因素分析

横向扫描敏感子弹的探测识别过程是包含敏感器光电探测、数据采集、信息处理的复杂过程，由于敏感器固有的延迟，识别目标总是滞后于扫描目标，这一滞后时间称为识别延迟时间；敏感器给出识别信号后，战斗部延迟一段时间才会起爆，这段时间称为起爆延迟时间。如果威力轴与敏感轴重合或平行，当敏感器识别目标并发出起爆指令后，威力轴将偏离识别点位置；同时， 爆炸成型弹丸(EFP)的牵连运动也会造成命中位置的偏移。因此需要将敏感轴前置于威力轴一个合适的角度，从而使威力轴对准目标位置，提高EFP对目标的命中概率。

3.1.1延迟时间造成的偏差

子弹发射后，在飞行中高速旋转。假设在识别延迟时间t1内，子弹转过角度为δ1，飞行距离为l1，在起爆延迟时间t2内，子弹转过角度为δ2，飞行距离为l2，由于延迟时间很短，可认为子弹速度近似不变，在理想情况下，延迟偏差表示为：

(3)

式(3)中，ωz1、v分别为子弹绕弹体轴的转速和飞行速度。

3.1.2EFP牵连运动造成的偏差

横向扫描敏感子弹的上抛运动可正交分解为绕弹轴的旋转运动和沿铅锤轴方向的质心运动。假设战斗部起爆后，牵连运动使得威力轴在弹体切向方向偏离δ3角度，如图5所示，图5中A为子弹质心，B为EFP瞄准点，C为命中点，威力轴从B扫描到C点的时间很短，螺线的收缩距离可以忽略不计，可以将△ABC近似为等腰三角形，故δ3表达式为：

(4)

式(4)中：d为战斗部药型罩到子弹质心的距离；vEFP为EFP起爆后的初始速度设计值。

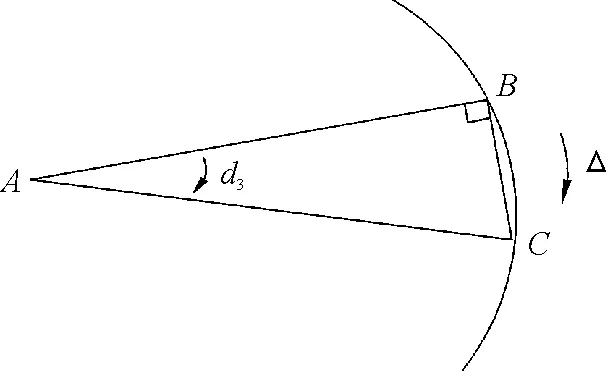
图5 EFP牵连运动引起的切向偏移示意图

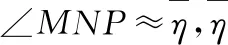
(5)

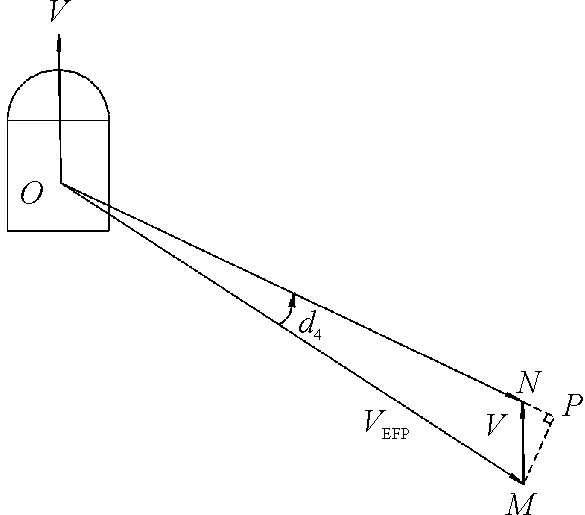
图6 EFP牵连运动引起的轴向偏移示意图

3.1.3前置角的设计

延迟时间均为毫秒级，取t1=1 ms，t2=0.1 ms，v=40 m/s，则l1+l2=0.044 mm，使敏感器的安装位置在弹体轴向偏离战斗部0.044 mm，即可抵消该误差。其他偏差可通过敏感器相对于战斗部的前置角进行补偿，敏感器的切向前置角δt和轴向前置角δa分别表示为：

(6)

3.2 敏感轴端点的扫描轨迹方程

敏感器与弹体保持相对静止，将弹体坐标系旋转δt角度，得到扫描坐标系Ox2y2z1，再将扫描坐标系坐标原点移至敏感信号发射点，得到了敏感坐标系Sx3y3z3，如图7所示。记敏感轴长度为ls，扫描信号发射点S在弹体坐标系中的位置为(lsox,0,lsoz)，子弹质心在地面惯性坐标系中的坐标为(x0,y0,z0)。将敏感轴端点在扫描坐标系下的坐标转化到基准坐标系下，再加上质心的位置，即得到敏感轴端点在地面惯性坐标系下的坐标S，即：

(7)

式(7)中，L-1(α)L-1(β)L-1(γ+δt)为扫描坐标系到基准坐标系的转换矩阵。

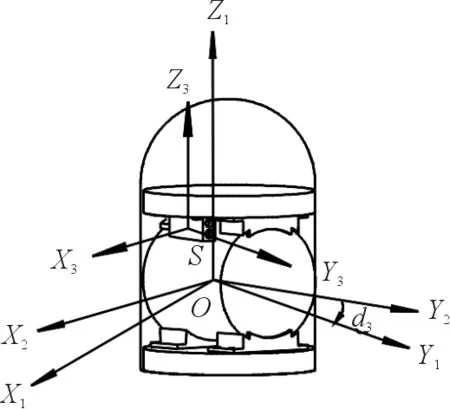
图7 稳态扫描模型示意图

由于子弹在飞行中存在周期性摆动，故敏感轴可能会接触到地面，被地面阻隔，此时敏感轴的长度ls不再为定值，其大小Sz=0时的值，记为ls1；当敏感轴扫描到目标时，敏感轴的长度ls也非定值，其大小为ls2=D，D为弹目距离。 将式(7)与六自由度弹道方程组联立，采用龙格库塔法迭代求解，即可得到敏感轴的空间运动轨迹及弹道诸元随时间的变化规律，如图8所示。

3.3 目标识别的判定条件

地面封控弹药的攻击响应时间很短，0.1 s内足以打击地面目标，目标机动距离很短，可假设目标做匀速直线运动，目标在竖直平面内的投影运动方程为：

(8)

式(8)中：(X,Y,Z)为目标边缘的tZ时刻位置；(X0,Y0,Z0)为目标中心的初始时刻位置；(Vx,Vy,Vz)为目标速度；(a,b,c)分别为目标的长、宽、高；t为子弹识别到打击目标所经历的时间。

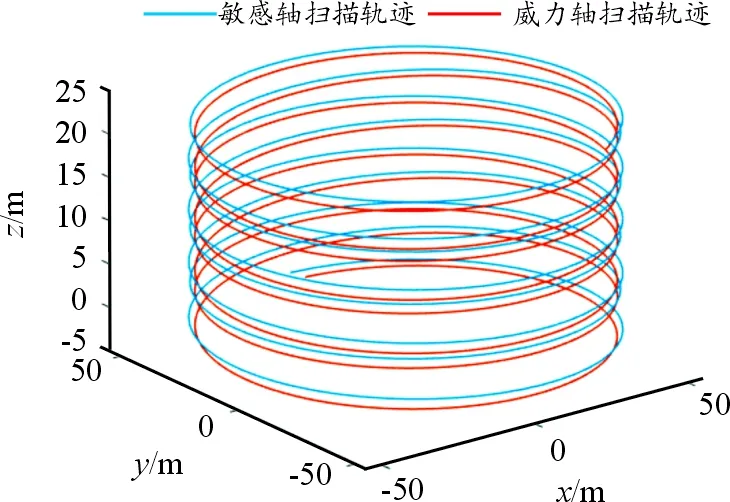
图8 敏感轴和威力轴的扫描轨迹示意图

子弹进入稳态扫描阶段后，激光/红外复合敏感器探测目标，弹载信息处理单元分析和处理敏感器响应信号，实现对目标的识别和定位。为了避免打击到目标的边缘，扫描目标的高度和宽度均需限定在一定阈值内。在一个扫描周期内，识别条件为：

(9)

式(9)中：H表示目标的判断(H=1表示金属目标，H=0表示非金属目标)；e是扫描识别区系数；L表示敏感器扫过目标的长度；Lmin是最小识别长度。

3.4 EFP命中点计算

EFP起爆后，由于战斗部自身的误差以及各种外部因素的干扰，战斗部命中点产生散布，记EFP命中点相对于瞄准点的中间偏差为Ex、Ey、Ez，EFP飞行距离为lv。威力轴位于弹体系Oy1z1平面内，与O-y1轴重合，将威力轴端点在弹体坐标系下的坐标转化到地面惯性坐标系下，再加上质心的位置与命中点的散布，即得EFP命中点在地面惯性坐标系下的坐标V为:

(10)

式(10)中，ξx、ξy、ξz为服从N(0,1)的随机数。联立式(11)与六自由度弹道方程组，即可得到t时刻EFP的命中点坐标。

为了避免打击到目标的边缘，目标区域需限定一个阈值，记有效命中区系数为e1。在一个扫描周期内，命中条件如下：

(11)

联立方程式(1)、式(6)～式(11)，即得到横向扫描敏感子弹的命中模型。

4 命中概率分析

在建立上述捕获识别模型与起爆命中模型的基础上，采用Monte Karlo法，模拟横向扫描敏感子弹对车辆目标的捕获识别、起爆命中过程，比较不同影响因素下的捕获识别与命中情况，统计得到了横向扫描敏感子弹的命中概率。命中概率的计算流程如图9所示。

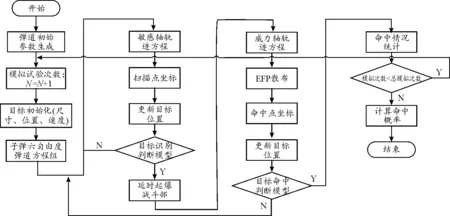
图9 命中概率计算流程框图

已知初值条件为：子弹初速为v=50 m/s，转速为ωz1=12 r/s，识别区域系数e=0.8，最小识别长度Lmin=1.2 m，响应延迟时间为1.1 ms，轴向补偿角为δa=-0.05°，切向补偿角为δt=4.7°，赤道转动惯量A=0.009 9，极转动惯量B=0.010 3，C=0.005 0，惯性积D=7e-5，初始扰动均为0.05 rad/s，EFP的中间偏差Ex=Ey=0.05。车辆目标在竖直平面内的投影尺寸为3.4 m×7 m，目标运动速度为20 m/s。

4.1 初始扰动对命中率的影响分析

子弹有效打击区域是圆形，假设目标沿该区域切线方向运动，不考虑推力偏心的影响，仿真计算了子弹初始扰动为0 rad/s、0.01 rad/s、0.02 rad/s、0.03 rad/s、0.04 rad/s、0.05 rad/s时，对20～50 m范围内运动目标的命中率，计算结果如图10所示。

由图10可知，横向扫描敏感子弹的命中概率随弹目距离的增大而降低，且子弹的初始扰动越大，对同一目标的命中概率就越低，这是因为初始扰动越大，扫描过程中子弹的平均摆动角越大，扫描螺距越不均匀，使得扫描识别与命中目标越发困难。当初始扰动小于0.01 rad/s时，子弹对不同距离目标的命中率均在72%以上；当初始扰动大于0.05 rad/s时，命中率均低于75%。

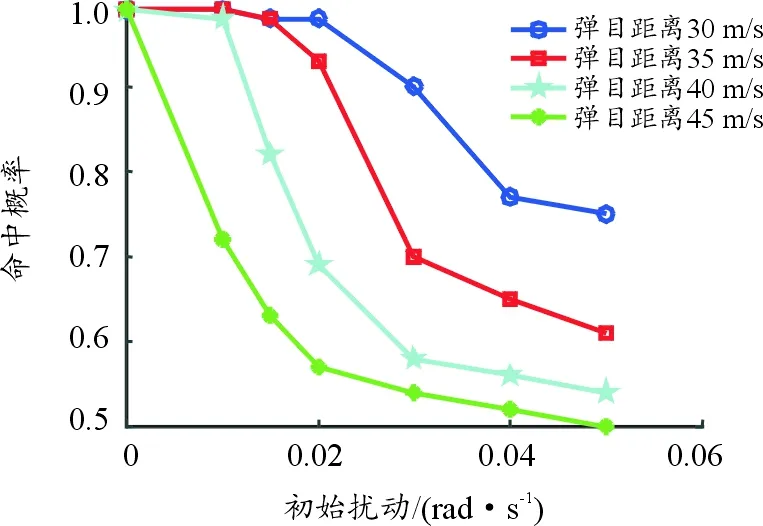
图10 不同弹目距离下命中概率随初始扰动的变化曲线

4.2 识别阈值对命中率的影响分析

假设敏感子弹的初始扰动均为0.05 rad/s，弹目距离为40 m，目标沿弹体径向方向运动，其他假设条件均与初值条件相同。仿真计算了子弹识别区系数分别为0.6、0.7、0.8、0.9时，最小识别长度取0.8～1.3 m的目标命中率，计算结果如图11所示。

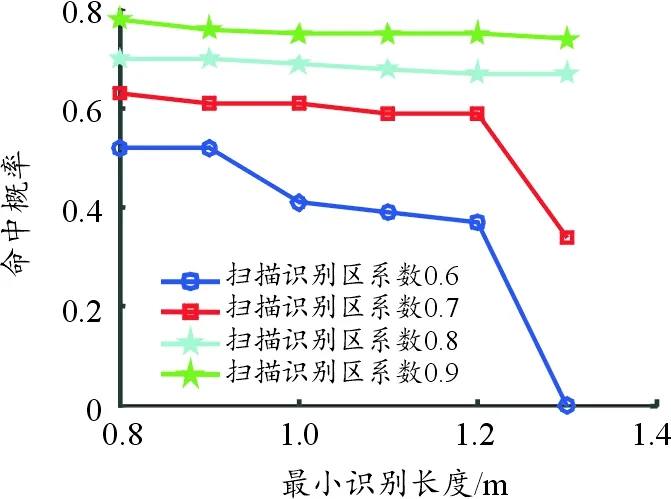
图11 不同扫描识别区系数下命中概率随最小识别长度的变化曲线

由图11可知，横向扫描敏感子弹的命中概率随着扫描识别区系数的增大而降低，且在最小识别长度提高到一定阈值时，命中概率陡然下降，其原因主要是：在较低的识别区系数下，目标识别区域相对较小，最小识别长度增加会提高识别难度，使子弹更难以捕获目标。因此需要搭配合理的识别阈值。当识别区系数大于0.8时，0.8～1.2 m的最小识别长度均适用，且命中率都在67%以上。

4.3 目标方位对命中率的影响分析

目标相对弹体的不同方位运动时，子弹的有效识别区域大小不一，导致了不同的命中概率。假设目标分别沿弹体切向和径向方向运动，其他假设条件均与初值条件相同，仿真计算了弹目距离取20～45 m的目标命中率，计算结果如图12所示。

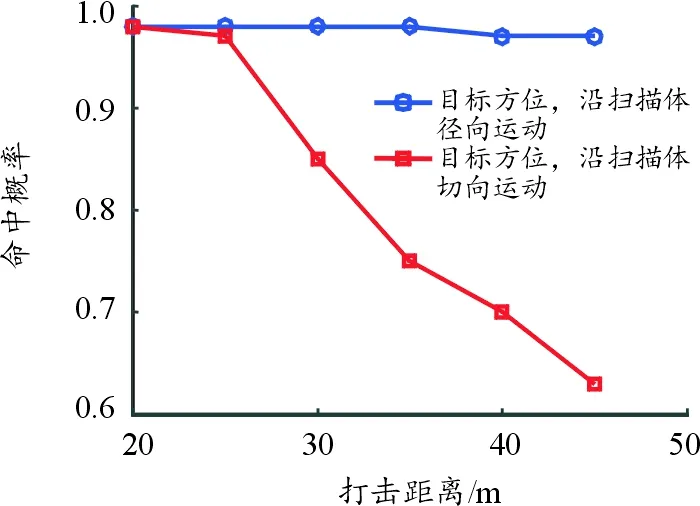
图12 不同目标方位下命中概率随弹目距离的变化曲线

从图12可以看出，目标沿弹体的切向方向运动时，弹目距离几乎不影响命中概率，这主要是因为切向运动的目标提供了冗余的识别长度，容易满足识别要求；而目标沿弹体的径向方向运动时，随弹目距离的增加，子弹命中概率急剧下降，这主要是因为有效目标区域已经接近识别长度，在弹体摆动的情况下，弹目距离越远，子弹越难以捕获目标。当弹目距离小于25 m时，目标方位对命中率影响不大；当弹目距离大于25 m时，应尽量选择位于切向方位的子弹进行打击。

4.4 最大摆动角对命中率的影响分析

假设目标沿弹体切向方向运动，其他假设条件均与初值条件相同。仿真计算了子弹最大摆动角分别为1.12°、1.57°、1.79°、2.20°时，弹目距离取20～45 m的目标命中率，计算结果如图13所示。

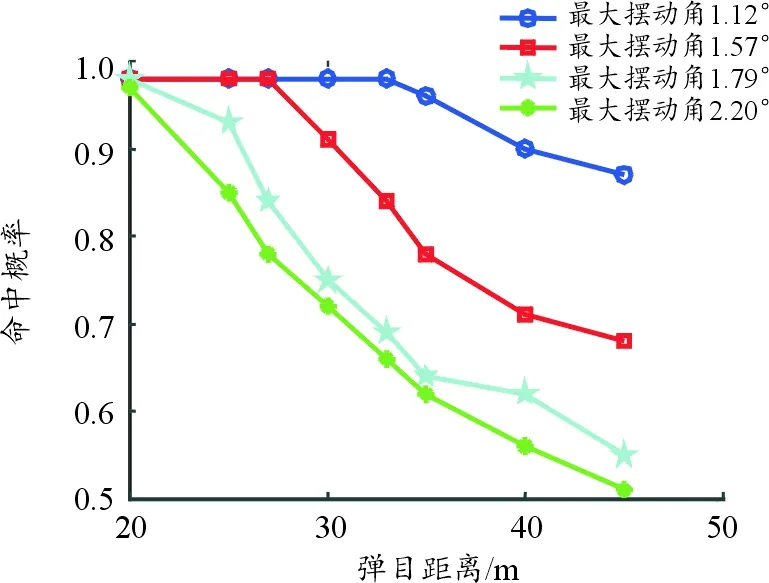
图13 不同最大摆动角下命中概率随弹目距离的变化曲线

由图13可知，对于25 m以内的目标，最大摆动角的变化对目标命中概率的影响有限，其命中率均在0.93以上，这是因为2°以内的摆动角，最大扫描间隔在1.8 m以内，未超出目标高度，子弹在扫描过程中可以有效捕获并命中目标；当弹目距离大于 时，随着弹目距离和摆动角的增加，目标命中概率大幅下降，这主要是因为扫描间隙的增加，使得捕获目标越来越困难。 当初始扰动小于0.05 rad/s，最大摆动角小于1.12°，弹目距离小于35 m时，子弹对目标的命中率均在93%以上。

5 结论

1) 目标命中概率随子弹初始扰动、最大摆动角和弹目距离的减小而增加，当初始扰动小于0.05 rad/s，最大摆动角小于1.12°，弹目距离小于35 m时，子弹对目标的命中率均在93%以上；

2) 目标命中概初始扰动随识别区系数的提高而增加，合理的搭配识别阈值能有效提高目标命中概率，当子弹初始扰动为0.05 rad/s，弹目距离为40 m，识别区系数大于0.8时， 0.8～1.2 m的最小识别长度均适用，且命中率都在67%以上；

3) 当目标沿弹体径向方向运动时，命中概率随弹目距离的增加而急剧降低，当弹目距离大于25 m时，应尽量选择位于切向方位的子弹进行打击。