基于粗糙集的北部湾区域物流发展协调性评价

李柏敏, 翁世洲, 吕跃进

(1.广西民族师范学院 经济与管理学院,广西 崇左 532200; 2.广西大学 数学与信息科学学院,广西 南宁 530004; 3.柳州工学院 数理教学部,广西 柳州 545616)

0 引言

作为广西重要的经济圈，北部湾经济区的发展对于拉动整个广西经济发展，促进广西进出口贸易具有重要意义。现代物流业作为区域经济发展和进出口贸易发展的主要推手起到了至关重要的作用，但区域物流与区域经济的发展往往存在不同步的情形，致使二者不能形成良性互动，甚至互相掣肘。因此，本文试图对北部湾经济区乃至整个广西区的区域物流与区域经济发展问题进行研究，给出协调性研究的评价结果，为后续政策研究提供参考和借鉴。另一方面，从技术层面，当前对协调性评价的相关方法以耦合模型为主，粗糙集作为一种模糊、不确定问题的有效工具虽获得广泛关注，但是在物流评价的相关领域并不多见。且粗糙集下的序信息系统在处理缺失数据时过于严格的标准往往会使得方法失效，故本文将从理论与应用两个层面对粗糙集下的区域物流发展协调性问题做一些探索和研究。

1 国内外研究现状

关于物流发展的协调性问题，目前已取得较多成果，主要如下：文献[1]运用复合系统模型(功效系数)对中国东、中、西部地区的物流业与经济发展协调度进行研究。文献[2]运用系统动力学方法探讨了广西区域物流和社会经济协调发展情况，认为应从刺激需求、合理投资和大力培育人才等措施入手以推动物流和经济之间的协调发展。文献[3]运用共生理论分析物流产业与区域经济协调发展的关系，认为其相互之间的合作大于竞争，主要的不协调在于发展不同步的问题，并提出了相关对策。文献[4]借鉴物理学中的耦合概念，研究区域物流与区域经济之间的协调度，认为不同区域之间的差异较大，东部地区协调度较高，而中西部地区物流发展水平高于经济发展水平，基本处于失调状态。文献[5]通过熵值法研究了新疆工业化进程与物流发展的协调度，得出二者目前是失调的结论并给出了相关建议。文献[6]通过加权模糊隶属函数法得出我国现代物流业与经济低碳化的协调发展从2005年以前的轻度失调乃至严重失调逐步实现协调发展甚至达到了优质协调。文献[7,8]通过运用大系统的多级递阶结构探讨了制造业与物流业的协调发展问题，并以佛山市为例，指出制造业与物流业之间的协调度在不断改善，走上良性发展的轨道。总体而言，关于物流发展的协调问题研究已有一些成熟的成果，主要是从物流与经济或其它行业的协调性入手展开讨论，这为本文的研究奠定了基础。

关于对北部湾经济圈物流发展的研究，目前相关文献并不多见，如文献[9]对北部湾港口物流产业集群发展模式进行了相关讨论，认为应重视北部湾港口之间的协同发展，整合北部湾物流资源以构建物流联盟，通过建设公共物流系统实现港口物流的跨越式发展。文献[10]针对北部湾经济区的商流与物流整合问题展开研究，通过分析其优势及存在的问题进而提出了整合商流与物流的相关策略。文献[11]基于DEA建立了评价北部湾区域物流效率模型，并进一步通过灰色预测模型GM(1,1)对其投入产出指标的未来发展进行了预测，认为在未来较长一段时间内都将处于效率低下状态，需要及时调整物流发展模式以提升效率。文献[12]则基于供应链视角对北部湾物流业转型升级策略进行研究，认为应从信息共享的内容、供应链战略的协调及利益分配机制等方面促进其转型升级。从相关文献可以看出，对北部湾经济区的物流发展研究主要集中在理论分析上，如资源整合、转型升级等问题上，而对区域物流与区域经济发展之间的协调性研究较为少见。

关于粗糙集理论下的协调性问题，近年来也取得一些研究成果，如文献[13]讨论了不协调广义多尺度决策系统的尺度组合问题，文献[14]研究了广义协调距离表示空间及其属性约简问题，文献[15]提出了直觉模糊决策系统的一种变协调度粗糙集模型，这些成果都对完善粗糙集模型中的协调性问题具有参考借鉴意义。另一方面，关于将粗糙集理论应用于物流领域的情形，目前也有一些成果，如文献[16]利用粗糙集理论和盲数测评模型，通过建立评价指标体系，对第三方物流企业的竞争力进行了相关研究。文献[17]结合BP神经网络和粗糙集方法对制造业协同物流绩效评价问题进行研究，评价结果可为制造业协同物流管理者提供有效运作与实施的建议。文献[18]将粗糙集理论和遗传算法与支持向量机理论结合使用，用于预测广东省未来的物流需求，结果显示加入了粗糙集约简和遗传算法寻优时拟合结果不仅具有更小的均方误差，且具有相对更快的计算时间。此外，文献[19]将粗糙集用于物流资源分类方法的研究中，并给出了相应的约简算法和分类规则。文献[20]将粗糙集应用于电商物流服务质量评价中。从现有文献来看，尽管有不少学者对粗糙集理论与方法有所提及，但是对该理论的应用主要集中在属性约简，极少使用到优势关系的相关理论，而事实上，仅仅用保持正域不变的约简结果来处理具有序关系的决策系统是不科学的，甚至可能会导致结果与预期背离，相关情况说明可参考文献[21]。

文献综述表明，对物流发展的协调问题已有研究，但是对北部湾物流发展的协调性问题以及基于粗糙集理论对物流发展的协调性问题的研究还极为少见，故本文将以此为切入点，通过运用新的方法和技术手段去研究区域物流与区域经济发展的协调问题，相关方法对数据具有较强的容错能力，适用于实际研究中经常遇到的数据不完整的情形。

2 粗糙集理论

2.1 不完备序决策系统

定义1[23]称一个五元组为S={U,C,F,D,G}为一个决策信息系统，其中U={x1,x2,…,xn}为有限对象集，C={c1,c2,…,cm}为有限条件属性集，D={d1,d2,…,dp}为有限决策属性集，f={fk:U→Vk,k≤m}为U与C的关系集，Vk是属性ck的有限值域，G={gk:U→Vk′,k′≤p}为U与D的关系集，Vk′是dk′的有限值域。

若每个条件属性和决策属性上的值域均为偏序集，如一个班的各科成绩情况，企业收益率等，则此决策系统可称为序决策系统或序目标信息系统。若值域集合Vk、Vk′中存在未知值或缺省值，则以*表示，称含有*的序决策系统为不完备序决策系统，本文中仍将其记为S。参照文献[24]中概率优势关系的定义，在不完备序决策系统中，可做如下定义。

定义2设S={U,C,F,D,G}为不完备序决策系统，对∀xi,xj∈U,a∈A(A代表C或D，下同)，记

(1)

称pa(xi,xj)为对象xj相比于xi在属性a下取值的优势度，pa(xi,xj)=1表明在属性a下，xj的取值优于xi，pa(xi,xj)=0.5表明xj与xi不相上下，pa(xi,xj)=0表明xj劣于xi。则对象xj在全体属性集A下不劣于xi的优势度可记为

(2)

其中|a|表示占优的属性个数，即pa(xi,xj)中取值为1的属性，|b|表示xi与xj不相上下的属性个数，即pa(xi,xj)中取值为0.5的属性，|A|为全体条件属性集或决策属性集的数量。

性质1[24]关于pa(xi,xj)有如下结论成立：

1)∀xi∈U,pa(xi,xj)=0.5；

2)∀xi,xj∈U,pa(xi,xj)+pa(xj,xi)=1。

性质2[24]关于PA(xi,xj)有如下结论成立：

1)∀xi∈U,PA(xi,xj)∈[0,1]；

2)PA(xi,xj)=0⟺|a|=|b|=0；

3)PA(xi,xj)=1⟺|a|=|A|,|b|=0；

4)∀xi∈U,PA(xi,xi)=0.5；

5)∀xi,xj∈U,PA(xi,xj)+PA(xj,xi)=1。

定义3在不完备序决策系统S=(U,C,F,D,G)中，S在属性集A下的α-概率优势关系可定义为

(3)

其中α称为可信度。则相应的对象xi的α-概率优势类可记为

(4)

在式(3)中，α≤0.5表示“优于”的条件是至少半数原则，比如一共有10个指标，其中xj在某6个指标下均比xi的取值更优，则基本有理由相信xj优于xi。

在上述定义中，可信度α可根据决策者对风险的偏好灵活调整，若决策者属于风险厌恶型，对误差的容忍度较小，则宜取较大的α值，反之，减小α值可适当放宽对优势类的限制，所构造的优势关系具有更强的容错能力。

2.2 条件属性集与决策属性集的协调度

为了度量条件属性集C与决策属性集D之间的同步性和一致性，本节给出协调度的概念如下。

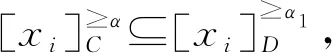
所谓协调的序决策系统，其本质含义在于：若对象xi在所有条件属性下的取值均优于(大于等于)xj，则其对象的决策属性值也应满足xi优于xj，这是系统评价与决策应满足的基本条件。

定义5在不完备序决策系统S={U,C,F,D,G}中，对象xi在条件属性集C下相对于决策属性集D的协调度可定义为

(5)

同理，对象xi在决策属性集D下相对于条件属性集C的协调度可定义为

(6)

对于协调度的概念及定义，可做如下解释：粗糙集理论下的优势关系一般主要用于解决优劣比较的排序问题，但现实中部分问题并非仅限于排序，相比之下协调性问题可能更为重要，以本文的研究背景而言，众所周知省会城市或较为发达城市的物流发展一般会领先于普通中小城市，但这种领先或优势是否与区域经济的发展水平相匹配则不是排序问题可以解决的。类似于DEA模型下的投入产出分析，协调性更多将从效率层面看待发展问题，即基于某地区当前经济水平下去评价其区域物流发展水平，而不是仅从绝对量对不同区域的物流发展水平进行评价。

性质4协调度ID(C/D,xi)与ID(D/C,xi)具备如下性质：

2.3 案例演算

为了使读者对不完备序决策系统中的优势关系与协调度有所了解，给出相关数据如表1所示。

表1 不完备序决策系统示例

由上例可知，各对象在条件属性集C下两两比较的优势度矩阵依公式(2)计算如表2所示。

表2 对象间两两比较的优势度矩阵PC(xi,xj)

进一步由公式(4)可算出各对象在条件属性集C和决策属性集D下的优势集为：

进一步由公式(5)(6)可求得对象x1在条件属性集相对于决策属性集的协调度，以及在决策属性集相对于条件属性集的协调度，例如：

同理可得其余各指标如表3所示。

表3 各对象协调度一览表

3 北部湾区域物流协调性分析

3.1 数据来源与符号说明

为了对北部湾各区域的物流发展协调性进行分析，本文选取了7个经济指标和7个物流指标，其中经济指标作为条件属性集以C表示，物流指标作为决策属性集以D表示，具体指标信息如表4所示。

要想从根本上提高衡阳市水稻生产水平，不仅要建立完整的种植管理监督机制，也要结合衡阳市实际情况，优化水稻种植技术。当地政府要组织相关部门对农户进行水稻种植技术的培训和指导，确保农户能真正体会到新技术类型产生的经济效益，从而推动水稻种植管理发展进程，实现经济效益和环保效益的共赢。

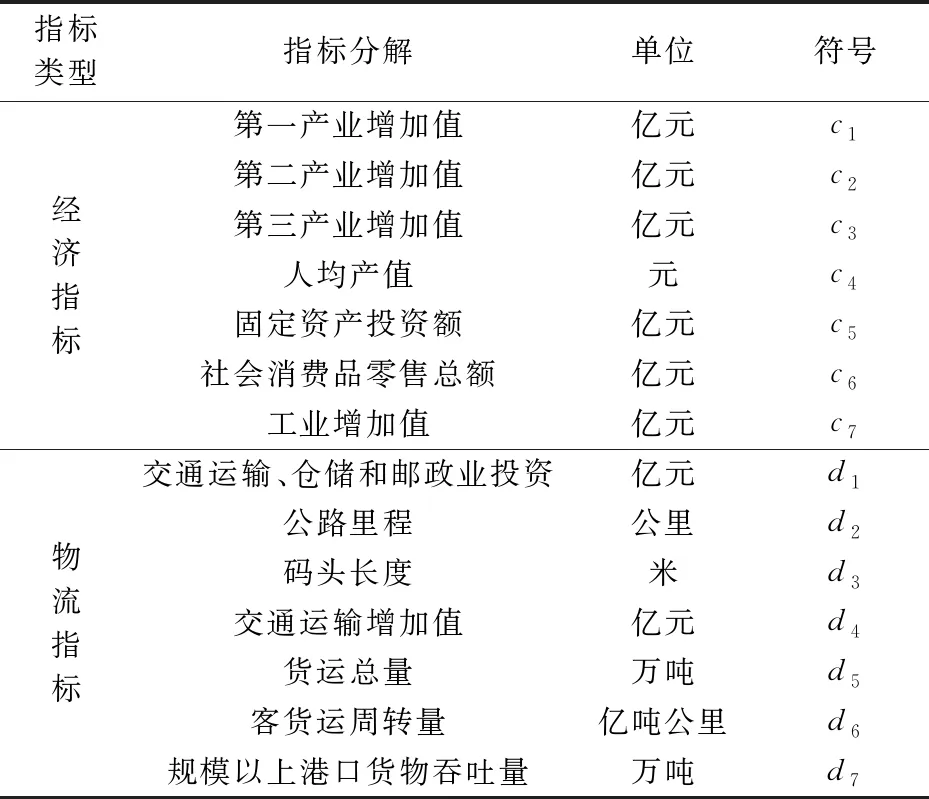
表4 经济指标与物流指标信息

从统计资料中搜集了2015年广西14个地级市的相关数据，各市区作为对象集U以表示，分别为百色市x1、北海市x2、崇左市x3、防城港市x4、贵港市x5、桂林市x6、河池市x7、贺州市x8、来宾市x9、柳州市x10、南宁市x11、钦州市x12、梧州市x13、玉林市x14。依照上述符号说明，相关数据如表5、表6所示，根据数据可获得性问题，部分缺失值以*代替。

由于粗糙集理论的相关方法不涉及到不同属性之间的数值运算，故针对不同属性的不同量纲问题，无需进行数据的标准化处理。此外，由于粗糙集理论可通过模糊的方法处理缺失值，而不用进行数据填充，也不需要因个别数据缺失而删除某个属性。

表5 各地级市经济指标数据一览表(属性集C)

表6 各地级市物流指标数据一览表(属性集D)

3.2 外部协调性分析

对上述数据，按照2.1节中不完备序决策系统中的概率优势关系可得各对象在条件属性集和决策属性集下的优势类如表7所示(为表达方便，将优势类集合中x的均做了省略，只保留下标)。值得说明的是，目前相似文献对可信度α的选取并无严格规定，如2.1节所述，可信度代表了决策者对风险的偏好程度，一般情况下只要满足“半数原则”即可通过，另外本文侧重于协调性求解，并非单纯追求优劣与排序，故在α的选取上不必过于严格，暂取α=0.5用于计算说明相关问题即可。

进一步，按照协调性的求解公式，可得表8。

表7 各区域在相应指标下的优势类

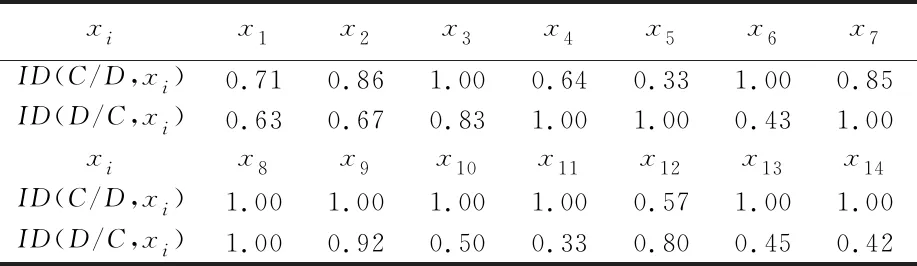
表8 各区域的协调度评价值

值得说明的是，ID(C/D,xi)表示经济发展相对于物流发展的协调性，即ID(C/D,xi)越小，表示对地区xi而言，存在较多经济发展领先于xi但物流发展却落后于xi的地区，即地区xi的物流发展水平领先于其经济发展水平，经济发展作为物流发展的基础显得不足。同理，ID(D/C,xi)表示物流发展相对于经济发展的协调性，ID(D/C,xi)越小，表示对地区xi而言，存在较多物流发展领先于xi但经济发展却落后于xi的地区，即地区xi的经济发展水平领先于其物流发展水平，物流发展作为经济发展的带动产业显得不足。

根据协调度的评价要求，可令ID=1为完全协调，ID∈[0.8,1)为高度协调，ID∈[0.5,0.8)为中度协调，ID∈[0,0.5)为低度协调。依此标准，则可得广西各地级市的物流发展协调性如表9所示。

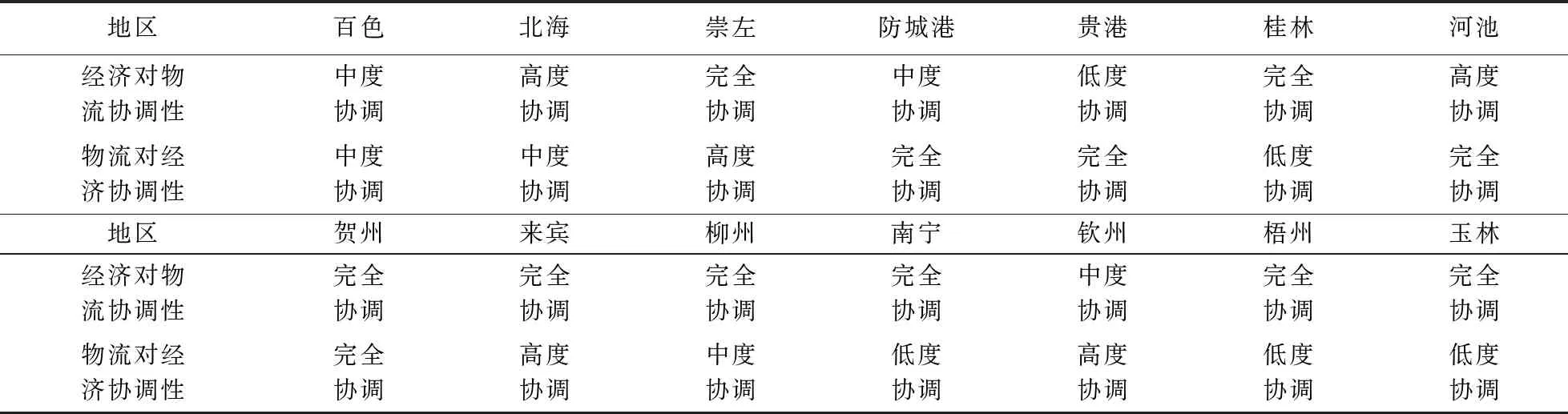
表9 各区域协调度评价结论

从表9可以看出，桂林、南宁、梧州和玉林4市处于物流发展水平显著落后于其经济发展水平的状态，柳州、北海2市处于物流发展水平略微落后于其经济发展水平的状态，防城港、贵港2市处于物流发展水平领先于其经济发展水平的状态，百色、崇左、河池、来宾、钦州5市物流发展水平与经济发展水平处于基本协调的状态，贺州市的物流发展水平与经济发展水平则极为协调，事实上，对于贺州市的协调状态，主要在于其经济发展水平和物流发展水平都极其落后，处在广西14个地级市末位，故而显得协调。

图1 经济对物流协调性空间分布图

图2 物流对经济协调性空间分布图

由图1可知，绝大部分地区经济对物流发展呈现出完全协调和高度协调，仅贵港、百色、钦州、防城港等地协调度较低，表明这些地区物流发展领先于经济发展的速度，需要进一步发展经济，从而更好地利用经济发展的动力支撑物流可持续发展，在地域上以西部地区为主。由图2可知，仅贵港、防城港、贺州、河池等地区协调度较高，尤其以桂林、南宁、梧州、玉林四市处于低度协调状态，表明这些地区经济发展速度领先于当地物流发展速度，当地的物流行业和企业优势不明显，没有充分利用当地经济发展的优势来鼓励和促进物流业发展，在地域上以东部地区为主。

3.3 内部协调性分析

为对北部湾经济圈内的四个地区进行对比，采用文献[24]中的排序方法，对广西14个地级市的区域物流和区域经济发展情况进行排名，并从中比较北部湾经济区下辖的南宁、钦州、北海、防城港四市发展情况，如表10所示。

表10 广西各区域物流与经济发展排名

将南宁、钦州、北海、防城港四市数据单独列出，则结果如表11所示。

表11 北部湾经济区各区域发展排名对比

从上表可以看出，在整体排名中，北海市、南宁市和钦州市区域物流与区域经济的发展相对协调(经济发展排名与物流发展排名相差不大)，但防城港市则显得较为不协调，物流发展水平明显领先于当地的经济发展水平，这与上一小节的分析结论一致。

另一方面，从北部湾经济区四市作为一个整体来看，无论是经济指标还是物流指标的发展都显得极为不均衡，南宁市作为省会城市，其发展水平遥遥领先其他三市。相比之下，钦州、北海均处于中等或中等偏上位置，防城港市物流发展依托港口优势成效显著，但是经济发展仍有较大增长空间，说明在广西所有地级市中，北部湾城市群具有一定的优势和广阔前景。

3.4 算法对比分析

由于一般理论和方法无法有效处理缺失数据的情况，也很难找到完全相同的文献数据，故本文将上一小节中的排序结果与文献[24]中的结果进行简单比较。首先将表8中的各城市的综合优势度C和综合优势度D的得分相加再从高到低进行排名，即为各地区的经济物流综合排名，文献[24]利用2014年广西各地区的物流和经济指标数据分析了其物流竞争力，也得到了各区域的排名，将二者对比可得如表12所示结果。

表12 本文与文献[24]排序结果对比表

从排序对比结果可以看出，尽管使用了不同的指标、甚至是不同年份的数据和排序方法，但是其排序结果基本一致，5个地区完全一致，8个地区排名相差一位，仅有1个地区(玉林)排名相差两位，这表明本文的排序方法具有相当的合理性和稳定性。

4 结论

通过本文分析可知，对于物流发展相对落后的区域，应充分利用其相对较好的经济基础，促进区域物流的进一步发展，而对于物流发展相对领先的区域，为了可持续发展战略，应把握当前的物流发展机遇，并刺激区域经济发展，以确保为区域物流的发展提供强劲动力，避免后劲不足。而对于目前物流与经济发展相对协调的区域，则应齐头并进，促进区域经济与区域物流同步发展，相互策应。另一方面，将粗糙集理论及优势关系引入物流决策领域，无需确定指标权重，并且对数据具有一定的容错能力，所得结果较为合理，今后笔者会将粗糙集相关理论应用于物流选址、物流配送等更多物流决策问题，不断完善和推广这一理论方法。