连杆转向阻力矩研究与实验
罗任峰,孙艳芳,张元萍,席晋东,周少东
(天津航天机电设备研究所,天津 300301)
0 引言
连杆转向在厂区内车辆的转向系统中应用比较普遍,其中转向杆的强度设计是关键。为了更好地设计转向杆,需要估计出转向轮的阻力大小。由于车辆的静态转向阻力比动态的转向阻力大2~3倍,所以以原地静态转向为设计工况[1]。目前比较常用的计算车辆原地转向阻力的计算公式有原苏联的半经验公式、雷索夫推荐公式和塔布莱克推荐公式[2],但上述推荐公式缺少对于实际原理的分析。文献[3]采用积分的方法进行了摩擦阻力矩的计算,对于接触面积进行了假设,但其所采用的积分方法对于转向阻力的分析在工程实际中有点复杂。本文在上述方法的基础上,对车辆原地实际转向原理进行了分析,并在假设聚氨酯轮接触面处摩擦力相同的基础上使用积分的方法计算聚氨酯轮的转向阻力矩,通过对连杆转向机构的分析得到连杆转向的力矩,并通过现场实物对实际连杆转向阻力进行测量,以验证该方法的正确性。
1 聚氨酯轮转向阻力矩计算
1.1 接触面积及应力定性分析
轮和地面的接触符合圆柱体和平面的接触分析模型,根据赫兹接触理论,可以计算出接触区域大小以及接触处的应力分布情况。假设轮的材质全部为聚氨酯(实际为内部铁芯外部聚氨酯),地面假设为结构钢,相应的材料参数如表1所示。

表1 材料参数
根据赫兹理论,圆柱与平面弹性接触时,其接触区域可以简化为长度为b、宽度为2a的矩形[4],按图1建立坐标系,轮胎和地面接触平面的中心线为y轴,与轮胎平行方向为x轴,x轴和y轴交点为坐标原点o,坐标指向如图1所示。

图1 圆柱与平面接触示意图
接触宽度a由下式计算[5]:

(1)
其中:N为轮受到的正压力,取6 250 N;R为轮的半径,取220 mm;b为轮胎宽度,取120 mm;ν1、ν2分别为两接触体的泊松比;E1、E2分别为两接触体的弹性模量。
接触应力p由下式计算:

(2)
其中:p(x)为受力点x的接触应力;x为受力点在坐标系中的x轴坐标值。
在上述假设的基础上可以得到,轮和地面的接触宽度2a大于10 mm,所以为面接触,并且各个位置处所受压力不同,为了计算方便,现假设所受压力每个截面相等,总的摩擦力大小表示为:
f=μN.
(3)
其中:μ为滑动摩擦因数,聚氨酯和地面的摩擦因数取0.4~0.7[6-8]。
1.2 轮胎阻力矩计算
根据上述接触应力分析,轮胎和地面的接触面积为一个矩形,接触面积大小与聚氨酯轮材料性能有关。轮转向原理及力矩计算如图2所示,假设围绕轮胎的中心进行旋转,单轮的转向阻力矩为接触面积内摩擦阻力的积分。以接触面积为研究对象,建立如图2所示坐标系,X轴和Y轴为接触面积的对称中心线,交点为坐标原点O,相应的积分可以表示如下[9]:

图2 轮转向原理及力矩计算
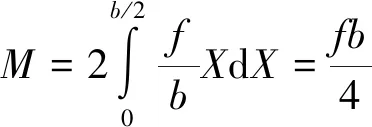
(4)
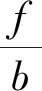
对于整个轮胎宽度进行积分即对X在(-b/2,b/2)范围内积分可以得到整个轮胎受到的阻力矩。
2 连杆转向阻力矩计算
第1节中,完成了轮胎阻力矩的计算,对于连杆转向机构来说,我们需要计算得到牵引的转向阻力矩,以此来确定牵引杆的长度,方便人员进行操作。图3所示为连杆转向机构,它主要由牵引杆、转向杆1、转向杆2以及转向轮组成。

图3 连杆转向机构
图3中,l0为转向轮力臂,F1为连杆驱动力,F2为人员操作力,L为牵引杆总的力臂长度,l为牵引杆长度,M为第1节所求轮的转向阻力矩。则有:
M=F1×l0.
(5)
2F1×(L-l)=F2×L.
(6)
联立式(5)和式(6)可以得到转向阻力矩和驱动力的关系:

(7)
轮胎的内、外转向角如图4所示[10]。连杆转向机构在转动的过程中,力臂是处于变化的过程中,假定内转角最大为20°,相应的外转角几乎为20°(该种连杆转向机构内、外转角几乎一致),所以可以按照20°进行轮转向力臂的计算,在转向过程牵引杆和转向力臂都处于变化过程中,由于变化角度接近,所以按照两者力臂不变考虑。同时考虑到在转动过程中转动副之间存在摩擦力,钢对钢的摩擦因数一般为0.1,本连杆结构有多处转动副,所以使用0.9的传递效率对式(7)进行修正,这样可以得到在转动过程中的最大转向力:

图4 轮胎内、外转角

(8)
3 转向阻力矩实验
实际设备重量2.5 t,使用铁芯聚氨酯轮胎,轮胎直径为400 mm、宽度为120 mm,试验场地自流平地面相对摩擦因数小,取0.4,相应的连杆转向参数如表2所示。

表2 连杆转向参数
根据公式(8),结合表2的参数值可以计算得到转向所需要的转向力为:
为了验证转向阻力公式的正确性,根据实际设备进行了转向阻力的测试试验。使用的测量设备为数显式推拉力计,其基本参数如表3所示。

表3 数显式推拉力计基本参数
根据现场情况,对设备进行了连接,相应的连接示意图如图5所示。

图5 现场转向阻力测试
测试过程中测量了多组数据,在转向过程中每个转角处力的大小不一样,其中在转角最大时力最大,刚开始启动时力有时也很大,4个测量位置的测量值如表4所示。其中,牵引杆和轮平行是0°,向右摆动是正角度,向左摆动是负角度,测量中取了其中4个位置的平均值。

表4 4个测量位置的转向力测量值
本文中推导的公式适用于求解最大转向阻力,所以对于测试过程的力取最大值和理论计算结果进行比较。测试数据显示转向阻力为121 N,理论计算结果为156.3 N,理论计算值和测量值误差在30%之内,表明转向阻力计算公式满足工程实际的使用要求。
4 结论
(1)本文使用赫兹理论对轮胎和地面接触进行了定性分析,分析出轮胎和地面接触面积的大致范围,为后期求解精确接触面积提供了一种思路。
(2)本文在假设各个接触面摩擦阻力相同的情况下,使用积分的方法对转向阻力矩进行了求解,并在此基础上进行了连杆转向机构牵引杆转向力的分析,得出了连杆转向力的计算公式。并通过现场实验的方法对连杆转向力的计算公式进行了验证,实验结果表明,误差在30%之内,满足工程实际的使用要求。
(3)本文对于连杆转向阻力的研究方法适用于对于转向力的粗略估计,如需要更加精确的结果需要对摩擦因数进行测量。

