基于模糊PID控制的车辆横向预瞄驾驶员模型*
武余利,张心奕,尹中亚,俞宴明,冉海风
(安徽工程大学 机械工程学院,安徽 芜湖 241000)
0 引言
驾驶员模型可以模拟驾驶员对车辆的横纵向控制,通过不断调整方向盘转角,使车辆能正常行驶。丁海涛等[1]提出最优预瞄加速度的单点预瞄模型,在方向控制上引入加速度反馈,建立了一个车道保持效果良好的驾驶员模型。李红志等[2]建立了预瞄时间自适应的单点预瞄模型。马军等[3]通过控制车辆的加速度,设计了模糊PID控制驾驶员模型。陈无畏等[4]建立了增量式驾驶员模型,并研究了车辆的单点预瞄控制策略,其方向盘转角为期望的方向盘转角与当前时刻横摆加速度之差除以稳态增益之和。以上几种单点预瞄模型主要研究了车辆侧向位移,未考虑实际汽车横摆角速度对方向盘转角不足的影响。为此,本文以理想与实际横摆角速度差为输入,对方向盘进行转角补偿,建立补偿式模糊PID控制驾驶员模型,并在CarSim和Simulink联合仿真环境下对车辆进行了仿真分析。
1 二自由度车辆动力学[5]模型
选取二自由度车辆作为本文仿真分析的模型,其状态方程为:
(1)
其中:m为整车质量;vx为纵向车速;Iz为转动惯量;k1为前轮侧偏刚度;k2为后轮侧偏刚度;lf为车辆质心到前轴的距离;β为车辆质心侧偏角;δf为前轮转角;ω为车辆橫摆角速度;a1=2k1+2k2;a2=2k1lf+2k2lr,lr为车辆质心到后轴的距离;a3=2k1lf2+2k2lr2。

(2)
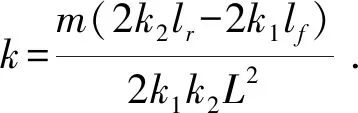
(3)
其中:L为前后轴间距离;k为稳定性因素;isw为角传动比。
2 单点预瞄驾驶员模型
在一段时间内车辆做圆周运动,汽车的橫摆角速度一定,由于横向车速vy几乎为零,可认为车辆的合速度等于车辆纵向速度vx。图1为恒定橫摆角速度的汽车行驶轨迹,建立大地坐标系XOY和车辆坐标系XGGYG,其中G点为车辆质心位置,Ψ为车辆的横摆角,P点为大地坐标系下期望轨迹的预瞄位置,Δf为预瞄偏差。实际行驶轨迹上点C在车辆坐标系下的横向偏差为:

图1 恒定橫摆角速度的汽车行驶轨迹
(4)
车辆行驶一段时间后,期望的车辆质心点P与点C重合,即yGC=Δf,转角θ=ωtp,yGC≈vxtp(tp为预瞄时间),则期望的橫摆角速度ωd为:
(5)
以此期望的橫摆角速度ωd和CarSim输出的实际横摆角速度之差作为方向盘转角补偿控制器的输入。
3 模糊PID控制器
3.1 补偿式模糊PID控制器结构
以车辆横向位移偏差作为控制器的输入,输出为方向盘转角,再以理想与实际的横摆角速度差作为输入,建立补偿式模糊PID控制模型,输出为方向盘转角补偿角,两者之和为车辆总的方向盘转角,然后输入到软件CarSim中。
3.2 输入输出变量的模糊子集
本模糊控制器[6]的输入和输出变量采用七个语言子集:NB、NM、NS、Z、PS、PM、PB。偏差E及偏差变化率EC在模糊控制器中的模糊论域均为[-1 1],比例系数ΔkP、积分系数ΔkI、微分系数ΔkD的模糊论域为[-3 3]。模糊控制器的输入E、EC及输出变量ΔkP、ΔkI、ΔkD隶属度函数选高斯与三角形函数,在MATLAB中调用Fuzzy工具箱做出隶属度函数曲线,如图2、图3所示。
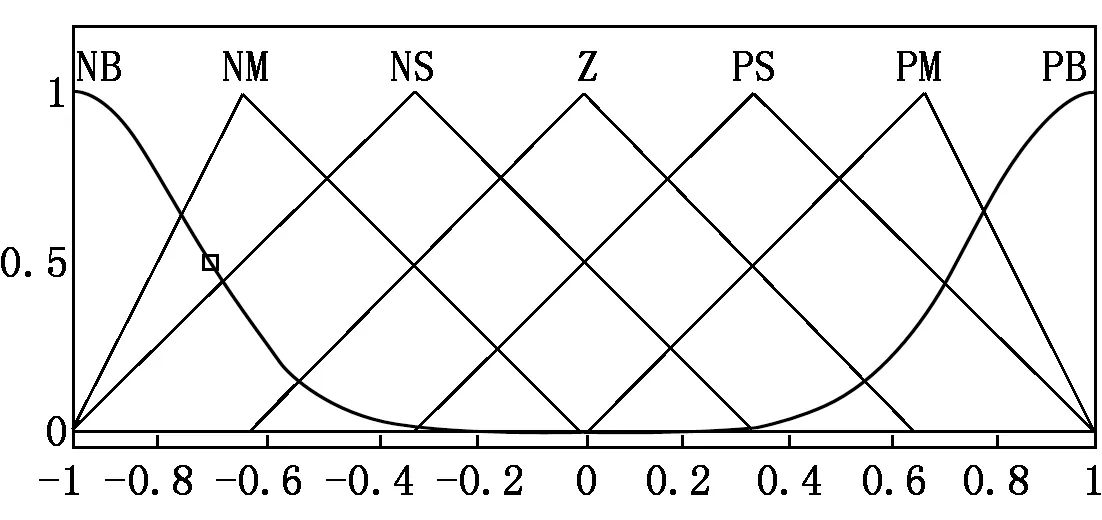
图2 E、EC隶属度函数
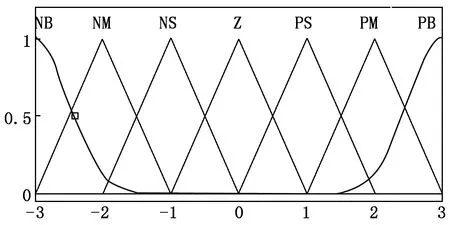
图3 ΔkP、ΔkI、ΔkD隶属度函数
3.3 制定模糊控制规则
参照上述分析中模糊控制器的自整定原则,综合考虑车辆单点预瞄的轨迹跟踪控制特性及专家知识经验选择模糊控制规则,如表1~表3所示。
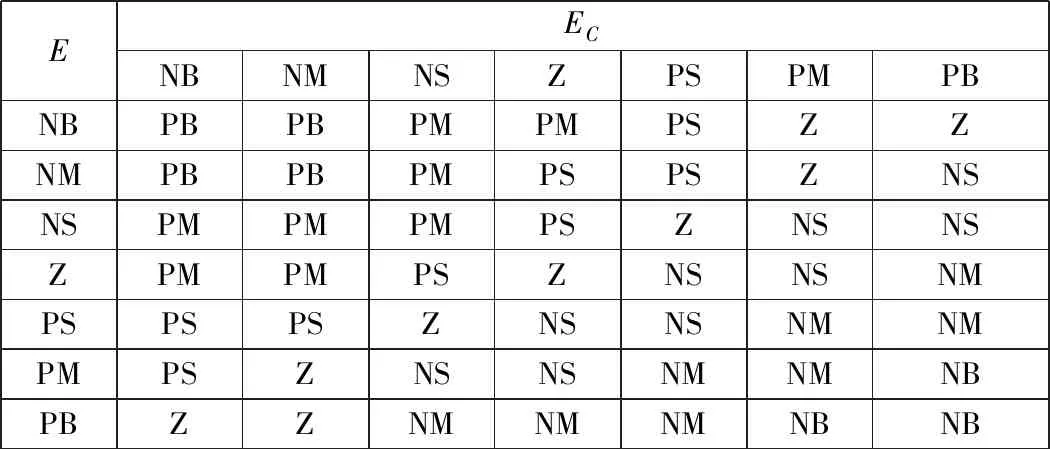
表1 ΔkP模糊控制规则

表2 ΔkI模糊控制规则

表3 ΔkD模糊控制规则
3.4 模糊推理和模糊判决
选择Mamdani推理法,采用极大极小值法算出模糊量的输出矢量。利用MATLAB模糊逻辑工具箱建立模糊推理。解模糊判决利用重心法,即:
(6)
其中:u为模糊控制器解模糊后的输出值;n为输出量化级数;vi为模糊控制器论域中的值;μk(vi)为vi的隶属度值。
在MATLAB/Simulink环境下搭建车辆方向盘转角补偿式模糊PID控制模型[7],如图4~图6所示。在系统运行效率的优化中,增加了零阶保持器,对模糊控制器的输入变量进行离散,以控制方向盘转角,确保车辆行驶的侧向偏差在一定的误差范围内。

图6 方向盘转角模型
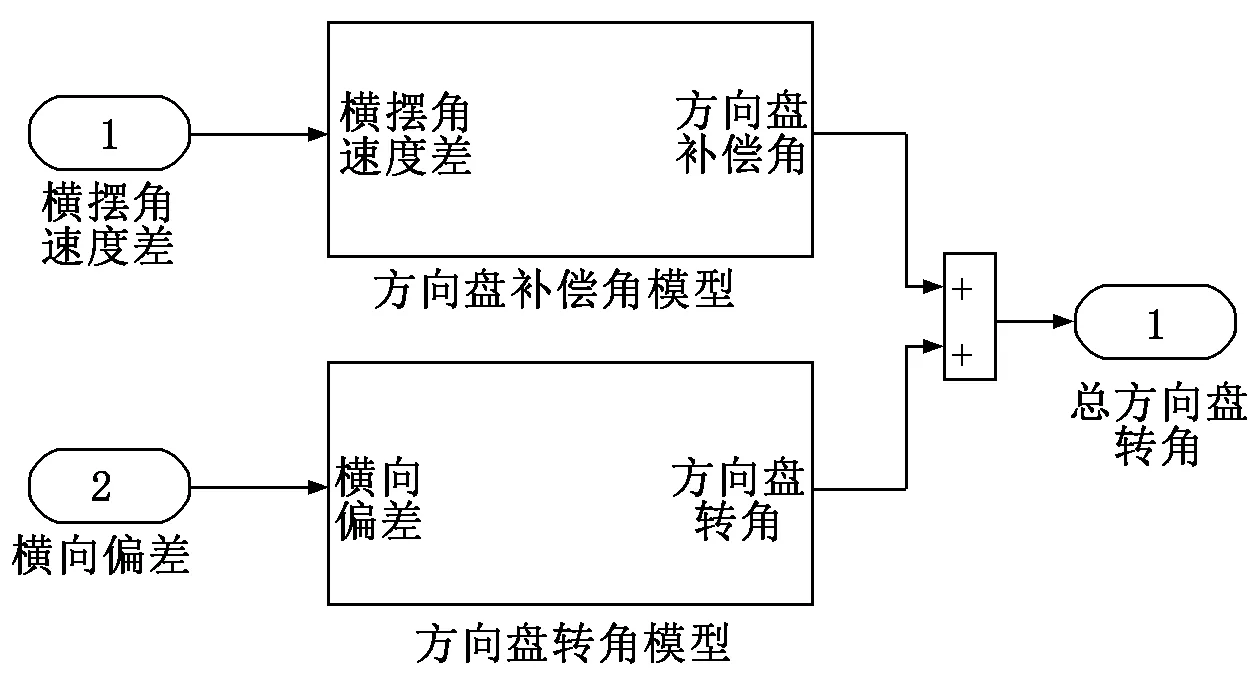
图4 模糊PID控制模型
4 仿真结果分析
选取S型仿真道路,在CarSim中设定车辆参数,如表4所示。在Simulink中搭建补偿式模糊PID控制驾驶员模型,路面附着系数为0.85,预瞄时间为0.5 s。对车速为70 km/h、30 km/h的车辆进行仿真分析,并与增量式驾驶员模型进行对比。

表4 车辆模型参数
4.1 车速为30 km/h
对车速为30 km/h的车辆进行仿真分析,得到的仿真结果如图7、图8所示。由图7、图8可知,PID控制、补偿式模糊PID控制、增量式驾驶员模型车辆最大侧向偏差分别为0.28 m、0.036 m、0.065 m,质心侧偏角均在-0.34°~0.34°之间。相比较于增量式驾驶员模型,补偿式模糊PID控制模型的控制精度在低速时提高了45%,在弯道时稳定速度最快。
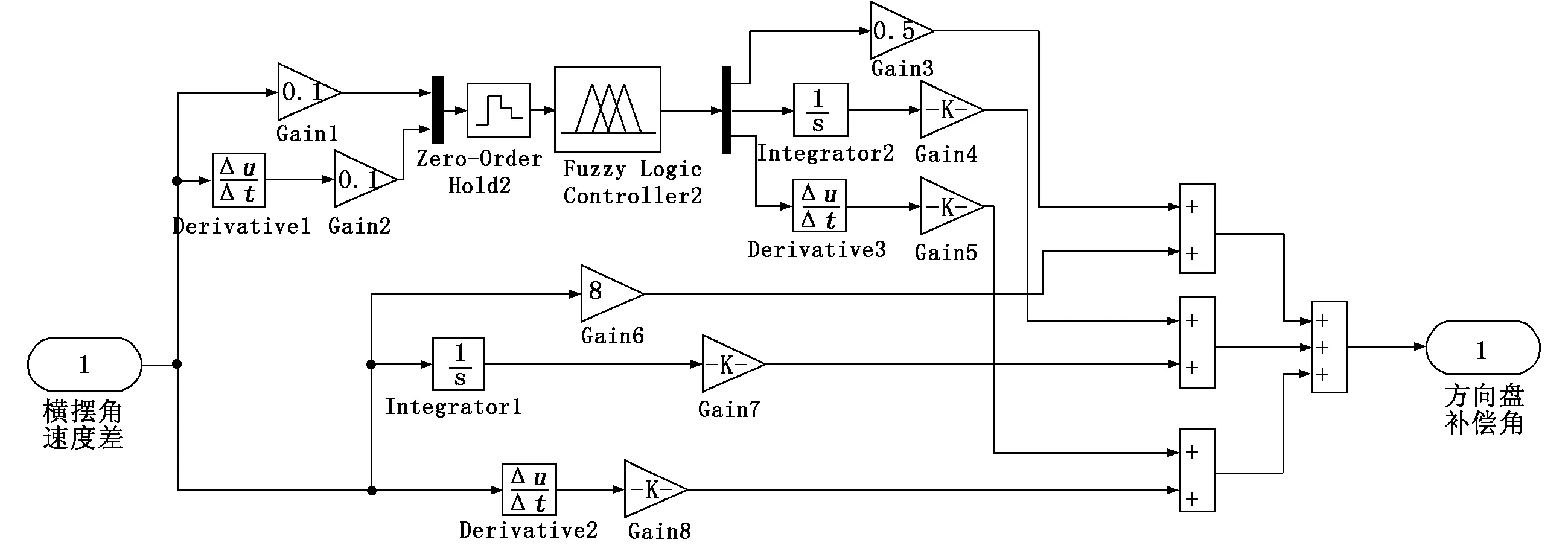
图5 方向盘转角补偿模型
4.2 车速为70 km/h
对车速为70 km/h的车辆进行仿真分析,得到的仿真结果如图9、图10所示。由图9、图10可知,补偿式模糊PID控制、PID控制、增量式驾驶员模型车辆最大侧向偏差分别为0.046 m、0.21 m、0.14 m,质心侧偏角分别为-0.16°~0.16°、-0.18°~0.18°、-0.15°~0.15°。可见3种模型在中速工况下补偿式模糊PID控制优于PID控制和增量式模型的路径跟踪。相较于增量式,补偿式模糊PID控制模型的控制精度提高了67%,在弯道处补偿式模糊PID控制模型曲线波动性明显低于其他两种模型。因此,补偿式模糊PID控制模型操纵稳定性[8]更优。

图7 转速为30 km/h的车辆侧向偏差仿真曲线 图8 转速为30 km/h的车辆质心侧偏角仿真曲线 图9 转速为70 km/h的车辆侧向偏差仿真曲线

图10 转速为70 km/h的车辆质心侧偏角仿真曲线
5 结论
本文假设横摆角速度一定,建立了补偿式模糊PID控制的车道保持模型并与增量式驾驶员模型比较。通过CarSim与Simulink对3种控制模型进行联合仿真,结果表明:补偿式模糊PID控制与增量式驾驶员模型对车辆行驶稳定性和车道保持都有很好的控制效果,相比于增量式驾驶员模型,补偿式模糊PID控制模型在低速和中速时控制精度分别提高了45%、67%。因此本文所设计控制模型具有更好的车道保持性能。

