一类非线性粘弹性Petrovsky方程柯西问题解的爆破

胡文燕

(晋中学院 数学系,山西 晋中 030600)

考虑如下非线性粘弹性Petrovsky方程的柯西问题

(1)

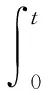
方程(1)可以解释很多重要的物理模型,很多学者已经对其解的整体存在性、渐近性、爆破性进行了大量研究[1-10].文献[1]对如下初边值问题进行了研究

(2)

其中：a,b>0,m≥2,Ω⊂n为一具有光滑边界∂Ω的有界区域,并且ν为其单位外法线方向.当初始能量为正值时,作者证得了其解在适当条件下会在有限时刻爆破的结论.并且,当初始能量消耗殆尽时,对于阻尼项为线性的情形,解仍会在有限时刻爆破.文献[2]通过对方程(2)源项和非线性阻尼项相互作用的研究,对解的下界进行了估计.

文献[3]对如下带粘弹性源项和强阻尼的Petrovsky方程的初边值问题进行了研究

(3)

当p>m时,其解在正的初始能量下在有限时刻会爆破,并且当p≤m时初边值问题(3)的解仍存在,推广了文献[1]的结果.

对于初始能量为非正值的情形,文献[4]讨论了如下方程的初边值问题,并得出了适当条件下解在有限时刻爆破的结论

(4)

对于非线性粘弹性Petrovsky方程,已有的研究成果[5-9]都是在有界区域内进行的.由于其解是可以由有界区域转移到无界区域的,那么研究Petrovsky方程在无界区域中解的爆破性质就显得尤为重要.为了得出无界区域内解的爆破情形,文章首先给出了松弛函数g满足的条件[10],并通过构造辅助函数,得出了其解在适当条件下在有限时刻会爆破的结论.

1 预备知识

(H) 假设松弛函数:g：+→+为一可微函数,满足

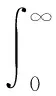
(5)

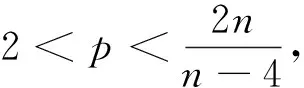
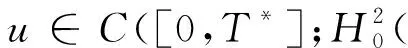
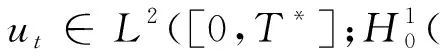
utt∈L∞((0,T*);L2(n)).

参考文献[11-13],运用Faedo-Galerkin方法,可证得柯西问题(1)解的存在性与唯一性,证明略.

定义方程(1)的能量函数[14]E(t)如下

(6)

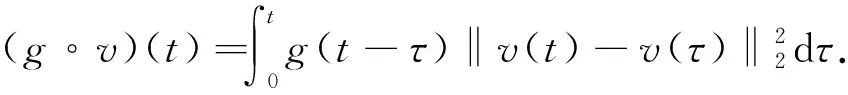
引理1假设g满足条件(H),且u(t)为柯西问题(1)的解,那么

证明将方程(1)两边同乘以ut,并在n上积分,可得

(7)

由

有

(8)

由(7)，(8)式，得

(9)

即

E′(t)≤0.

(10)

证毕.

引理2[15]假设Ψ∈C2()满足

其中：常数C0,L>0,α>0,-1<β≤0,那么Ψ(t)在有限时间内会爆破.

2 主要结果

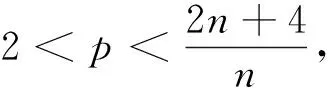
(11)

那么,对于任意初值(u0,u1),当如下条件

(12)

成立时，柯西问题(1)的解在有限时间内爆破.

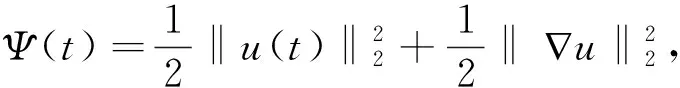
(13)

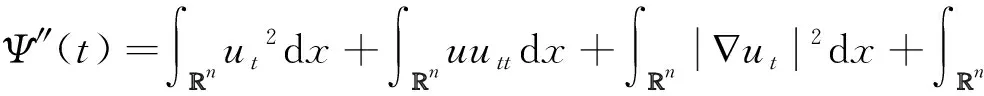
(14)

由方程(12)容易证得Ψ(0)>0,且Ψ′(0)≥0.再利用方程(1), 可以得到

(15)

将(15)式两边同乘以u(t),并在n上积分,有

故

Ψ″(t)+Ψ′(t)=

(16)

由Young及Hölder不等式,对任意的η>0,有

从而,对于任意的η>0,有

将其代入(16)式,整理可得

因为

所以

(17)

由能量函数E(t)的定义, 将下式

代入(17)式,有

因为(11)式成立,所以

由引理1,E′(t)≤0,又已知E(0)≤0,从而

E(t)≤E(0)≤0.

综上可得,存在γ>0,使得

(18)

运用Hölder不等式证明如下不等式

其中：L>0,B(t+L)是以原点为球心的球,且supp{u0(x),u1(x)}⊂B(L).

令Vn为单位球的体积,则

所以

(19)

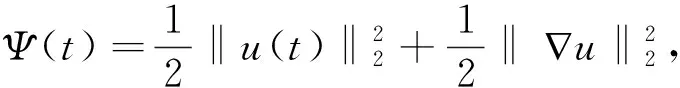
从而

即

(20)

将(19)，(20)式代入(18)式,有

根据(12)式及函数连续性,存在T*≤T*,使得

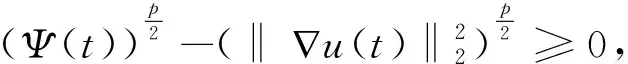
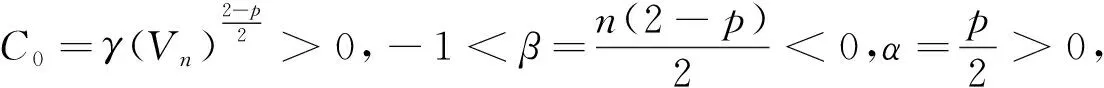
3 结束语

文章考虑了一类具有粘弹性和非线性源项的Petrovsky方程,在文献[5-9]的研究基础上做了推广,将其解由有界区域转移到无界区域.结果表明,当松弛函数和初值满足一定条件时,非线性源项足以导致其柯西问题解的爆破现象的发生.