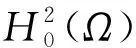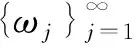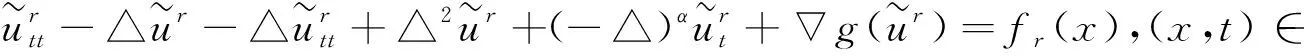具分数阶阻尼项发展方程解的长时间特点

张媛媛

(开封大学 信息工程学院，河南 开封 475000)

具阻尼项发展方程解的长时间特点一直以来都是偏微分方程研究的重点和难点,而对于具分数阶阻尼项发展方程解的探讨更是近年来这一研究领域中的热点问题.目前, 虽然对于这类方程初值问题和初边值问题的研究已经出现了一些成果[1-9], 但是此类方程作为耗散波传播的第一种非线性模型, 它的相关数学理论远不如Korteweg-de Vries型方程那么完整[10-13].

由于在无界区域下紧嵌入定理是不成立的, 所以处理一些先验估计比在有界区域情形下困难. 论文主要研究如下具分数阶阻尼项发展方程的Cauchy问题, 进一步探讨其解的长时间特点

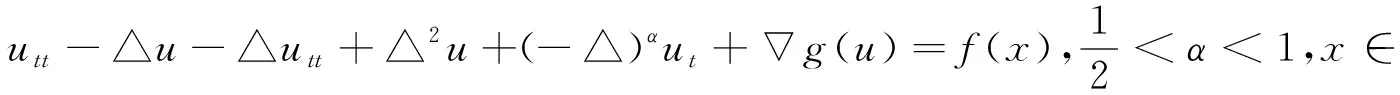
(1)

u(x,0)=u0(x),ut(x,0)=u1(x),x∈N.

(2)

方程(1)中涉及的非线性项是论文处理的重点和难点. 由于在无界区域下非线性项的估计受某些定理的限制, 因此利用有界区域Ωk的延拓， 在有界区域Ωk下, 结合算子半群对方程(1)中的两个非线性项进行估计, 证明解半群的渐近紧性及无界区域下整体解的存在性.

1 引理和定理

为书写简便,记下列简写符号

X(N)=H2(N)×H1(N),Lp=Lp(N),Ws,p=Ws,p(N),

其中：C代表不同的正常数,C(·)代表正常数依赖于括号内出现的数量.

引理1[14]设X是Banach空间,Ζ⊂C(+,X).Φ:X→是连续函数,且∃η,K≥0,∀z∈,有

假定∀z∈, 函数tΦ(z(t))是连续可微的,并且∃δ>0,k≥0,∀z∈, 满足微分不等式

引理2[14]设y:+→+是绝对连续函数, 满足下列不等式

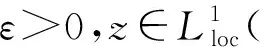
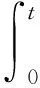
定理假定下列条件成立

(i)g∈C2(这里C1,C2是正常数.

(ii)f∈L2,(u0,u1)∈X(N),‖(u0,u1)‖X(N)≤r0.

则问题(1)，(2)存在唯一解u,且(u,ut)∈L∞(+;X(N)).另外, 解u满足下列特点

‖△u‖2+‖ut‖2≤C(r0,‖f‖),t≥0,

2 定理的证明

设Ω=Ωr是N中半径为r的球,有

‖·‖p=‖·‖Lp(Ω),‖·‖=‖·‖L2(Ω).

考虑问题(1)，(2)在有界区域Ω上对应的初边值问题

utt-△u-△utt+△2u+(-△)αut+g(u)=f(x),x∈Ω,t>0,

(3)

u|∂Ω=0,

(4)

(5)

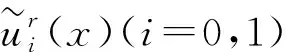
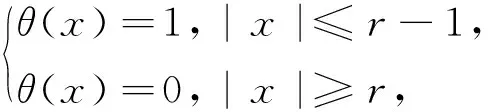
并且0≤θ(x)≤1,|△θ(x)|≤C,x∈N.

先对问题(3)～(5)的解作一些先验估计. 设

(3)式两边与ut+εu作内积,得

(6)

其中：ξu(t)=(u,ut)，有

ε(‖u‖2+‖△u‖2)+ε(g′(u)u,u)-ε(f(x),u).

然而，由假定(i),(ii), 得

(7)

有

将(7)式代入(6)式, 得

(8)

(8)式应用引理1，得

‖△u‖2+‖ut‖2≤C(r0,‖f‖),t≥t0=C(r0,‖f‖).

(9)

当t≤t0时, 对(8)式积分, 得

‖△u‖2+‖ut‖2≤C(r0,‖f‖),0≤t≤t0.

方程(3)两边关于t求导并令v=ut,得

vtt-△v-△vtt+△2v+(-△)αvt+g″(u)vu+g′(u)v=0.

(10)

(10)式两边与vt+εv作内积, 得

(g″(u)vu+g′(u)v,vt+εv)=ε(‖vt‖2+‖vt‖2).

(11)

其中

由g(s)的假定和嵌入定理, 得

|(g′(u)v,vt+εv)|≤C1((1+2ε)‖v‖2+ε‖v‖2)+

(12)

|(g″(u)vu,vt+εv)|≤C1‖v‖‖u‖(‖vt‖+ε‖v‖)+

(13)

(14)

当0

上式应用引理2, 得

(15)

当t≥1时, (14)式在(1,t)上应用引理2, 得

‖△ut‖2+‖utt‖2≤C(r0)e-kt+C.

(16)

由(15),(16)式，得

(17)

求问题(3)～(5)满足形式

(18)

(19)

C‖un‖p-1‖△un-△u‖+C‖u‖(‖un-u‖+

(20)

(21)

不难证明

(22)

(22)式两边与ωt+εω作内积, 得

(23)

其中

由假定(i)和嵌入定理, 得

(24)

(25)

将(24),(25)式代入(23)式, 得

于是

‖△ω‖2+‖ωt‖2≤Cekt(‖△ω0‖2+‖ω1‖2)+C(T)‖fri-frj‖2，

因此, (u,ut)∈L∞(0,T;X(N))是问题(1)，(2)的解. 由弱*极限范数的下半连续性知估计式(9),(17)式对u仍成立. 现在证明解的唯一性.

设u,v是问题(1)，(2)在空间L∞(+;X(N))上分别对应于初值(u0,u1)和(v0,v1)的两个解, 令z=u-v, 类似上面的证明, 得

‖△ω‖2+‖ωt‖2≤Cekt(‖△ω0‖2+‖ω1‖2),t∈[0,T]，

证毕.