基于CVaR的最优期货套期保值比率研究

文/胡泽岸（上海大学）

近年来，国内外市场股指、汇率和大宗商品价格均有剧烈且频繁的波动，其中大宗商品周期性更为强烈，对宏观经济依赖性更高，因此大宗商品投资者风险管理对冲的需要越来越迫切。本文主要的讨论内容就是利用不同估计方法获取最优套期保值比率并比较，探讨更适合目前国内期货市场的套期保值模型。

一、基于CVaR最小化的套期保值原理

（一）CVaR的定义

CVaR是指在特定时期内和确定的显著性水平下投资组合的损失超过VaR的条件均值。根据定义不难看出，CVaR天然具备绝对值必然大于VaR的特性，故其对极端损失考虑的充分性也必然是高于VaR的。而且CVaR作为一致性风险度量指标还具有次可加性，从多方面弥补了VaR方法的固有缺陷，又没有改变VaR简单有效的优势。在置信水平1-α下，以下公式可以简单清晰地表达CVaR的定义：

（二）CVaR模型原理

基于CVaR的套期保值模型原理与传统方差最小化基本一致，关键区别在于目标函数的优化选取。CVaR模型需要在套保者指定的显著性水平下,构建现货与期货的投资组合，每个组合都有各自特有的CVaR值。将CVaR作为目标函数,通过目标函数的最小化确认组合中的最优套期保值比率在置信水平1-α一定的前提下，套期保值组合的目标函数CVaR表达式如下：

假设Rh服从正态分布，对上式进行转化得——

其中, )(1αφ-为标准正态分布的分位数，则上式可转换为：

二、基于CVaR最小化的套期保值模型构建

（一）静态CVaR套期保值模型构建

通过对公式5求偏导来获得CVaR最小条件下的套期保值比率——

对上述等式求解能够获得两个不同的根式h1，h2，由下式表达——

得到上述两个解后，通过求二阶偏导进行检验，二阶偏导恒大于0，因此要求的套期比必然在两根之中，且CVaR(h1)≧CVaR(h2)恒成立，故h1对应的CVaR最小，故最优套期保值比率即为h1。在此基础上，再将协方差公式代入，可将其转换成以下表达式——

（二）动态化Realized-GARCH模型构建

将套期保值模型进一步从静态模型向动态模型演进，对其进行收益率分布的修正并动态化，可得到下式——

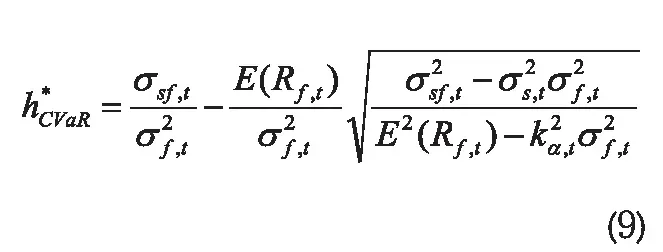
除了运用传统GARCH模型获取波动率，还需要将日内波动信息在模型中予以体现，主要通过已实现波动率即日内等时间间隔的收益率平方和来实现，其表达式如下：

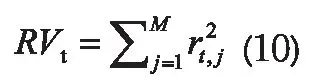
在传统GARCH模型和已实现波动率数据可获得的基础上，Realized-GARCH模型通过观测方程将已实现测度与条件方差相联系，形成一个封闭模型，从而实现GARCH族模型预测能力的较大提升。

Realized-GARCH(1，1)模型基本设定如下，其中xt即为高频已实现波动率估计量，本文选取RVt：

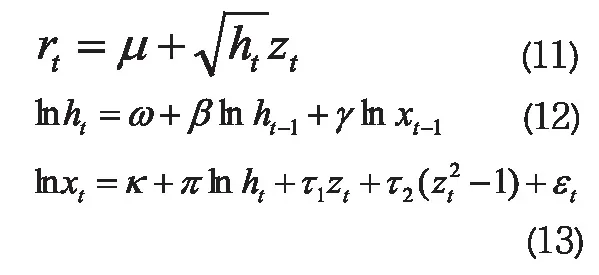
三、基于不同最优期货套期保值模型的实证分析

本文选取铜现货及期货日交易价格构建套期保值组合进行研究，对每日存在不同交割日期的期货价格数据采用日均交易价。本文选取2019-2020两年的年度日收盘价数据，即将2019年1月2日到2020年12月31日作为样本期。

（一）静态套期保值比率模型有效性分析

在选定的样本期内，通过构建两大类套期保值模型，即传统方差最小化模型、VaR族模型，从而获取相应的最优套保比。为确认模型效果，还需在样本期外增设检验期，进一步确认套保是否有效。选取方差减少比率He这一指标进一步比较不同模型进行风险对冲的有效性：方差较少比率越高，则套保的风险对冲效果越优异。具体公式见下式——

分别计算得出不同模型在样本期和检验期的检验效果指标He——

从表1样本期He指标数值可以看出，以VaR最小化为目标函数计算得出的最优套期保值模型对风险的对冲程度更高，OLS、B-VAR、ECM模型的风险对冲效果稍差一些。为了进一步验证有效性，选取2021年1月2日至2021年2月28日两个月作为检验期。从结果来看，同一模型获取的最优套期比在检验期的套期保值有效性低于样本期，这是符合一般逻辑及正常预期的。不过模型效果仍然保持较好，仍能对冲60%以上的风险。套期保值效果从高到低的顺序仍与样本期保持一致。其中，CVaR、VaR模型检验期套期保值效果甚至优于样本期。

表1 不同模型套期保值效果检验

（二）动态CVaR套期保值比率模型有效性分析

进一步采用Realized GARCH模型结合CVaR模型来进行套期保值，选取采样频率为5分钟的已实现波动率RV,从而更好反映日内波动信息。铜现货用极差收益率代替已实现波动率RV，仍能够反映现货价格的日内波动。

仍然选取方差减少比率作为有效性指标来衡量模型的套期保值绩效。另外，由于方差减少比率单纯从风险对冲角度来考虑，而VaR族模型由于其特有的模型性质能够进一步拆分风险和收益。因而，增加另一个绩效指标单位风险收益来综合考虑风险和收益。具体检验结果见表2。

从表2的检验结果来看，两类GARCH-VaR模型的套期保值效果均良好，且模型自身检验期效果基本都优于样本期；但样本期效果略差于上文其他静态模型，检验期模型效果则明显优于各静态模型。相比较而言，在动态框架下Realized-GARCH-CVaR模型效果更优，更能够综合考虑风险和收益。

表2 BGARCH-CVaR/Realized-GARCH-CVaR模型套期保值效果检验

四、结论

第一，在静态套期保值的框架下，样本期内CVaR及VaR最小化的最优期货套期保值比率小于传统方差最小化，且方差减少比率在样本期及检验期均高于其他模型。而CVaR又进一步克服了VaR的非一致性、非次可加性及极端情形失效的固有缺陷。一方面，CVaR最小化套期保值以更低的成本实现了更有效的风险对冲，提高了资本的利用效率。另一方面，CVaR模型特有的灵活性，可以适应不同投资者的收益需求和风险偏好。

第二，在动态套期保值的框架下，检验结果表明：一方面，两种GARCH模型效果良好，Realized-GARCHCVaR模型能够更好地拟合样本期和检验期套期组合的收益率分布；另一方面，就实际套保模型运用效果来看，Realized-GARCH-CVaR套期保值模型不仅能每日滚动对冲，具有较强的时变性，更包含了更多的日内波动信息，同时也保留了CVaR模型对风险和收益的兼顾和自主选择。

总体而言，以CVaR最小化为目标函数的动态套期保值模型为我国期货市场参与者的非金融企业、机构运用期货进行规避风险和投机获益提供借鉴的经验，具有重大意义。