精密抛光机磨头故障诊断方法
杜志峰
(山西太钢不锈钢股份有限公司 临汾分公司 山西临汾 041000)
1 引言
磨头是抛光机运行时最重要的工作部件,抛光机工作状况与加工零件的质量好坏有很大关系。当前抛光机存在的问题为磨头的振动大,容易引起整台机械设备的震动、噪音以及加工后的产品品质不稳定。在目前陶瓷机械装备越来越复杂、要求越来越高的情况下,寻找一个精确、完善的陶瓷机械设备故障诊断技术显得尤为重要和紧迫。
现有的故障诊断技术大都是利用 Fourier变换进行分析,它仅给出了一个信号统计的平均值,难以在时间、频率两个区域内同时获得全部和局部化结果。小波方法发展了窗口傅立叶转换的局域性思维,使整个图像和区域特性得到了很好的综合。由于所获取的抛光机磨头振波信号中存在着许多突变和大量噪音,而其奇异性和不规则的突变部分往往含有很高的信息量,利用小波方法能够全面、清晰地描述冲击过程中的局部时域特性及故障的时序过程,该技术具备局部定位能力,有助于进行故障分析和诊断。
2 磨头故障分析
为了研究信号能量的频率分布, 突出信号频谱图中的主频率,需要做功率谱分析[1]。在频率域中,根据巴什瓦尔定理(如式(1)所示),若积分收敛,则它代表e(t) 的总能量。
式中:|H(ω)|2通常称为功率谱或能量谱。
用Welch法估计功率谱密度,它是用改进的平均周期图法来求取随机信号的功率谱密度[2]。现场监测表明:在0~4kHz的频率范围内集中包含了磨头振动信号的信息。根据采样定理,对新磨头采用8kHz的频率进行采样。
3 精密抛光机磨头功率谱密采样
本文对信号进行功率谱采样的方法采用 Welch法估计功率谱密度,Welch功率谱密度是用改进的平均周期图法来求取随机信号的功率谱密度估计。现场监测表明,在0~4kHz的频率范围内集中包含了磨头振动信号的信息,根据采样定理,采用8kHz的频率进行采样[3]。
由图1可见新磨头的振动能量主要集中在800Hz以下,因此取分析频率范围0~1kHz,采样频率为2kHz重新进行分析。
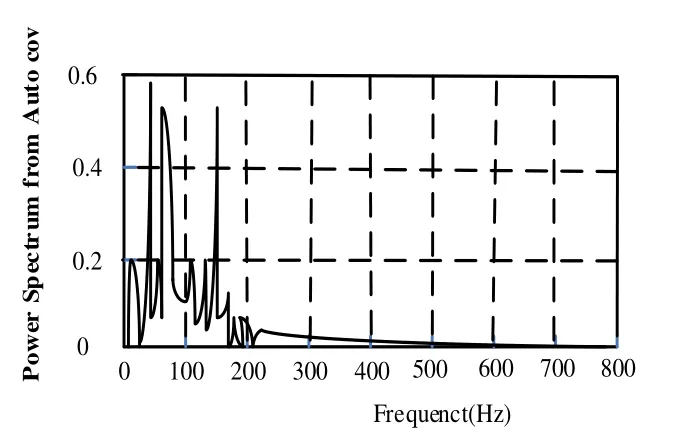
图1 新磨头垂直方向功率谱(线性坐标)
在不同的工作压力下,功率谱图在约2Hz处均有峰值,与凸轮与滚轮冲击频率相吻合。峰值较小反映新磨头的凸轮与滚轮的运动冲击不明显。
有关文献指出[4],齿轮传动信号频谱中,可能出现齿轮啮合频率及其谐频。经计算齿轮的啮合频率为321.17Hz,轴频为7.83Hz,可能出现的谱峰值有:啮合频率+1倍轴频=329.00Hz,对应图中的328.92Hz;啮合频率+3倍轴频=344.66Hz,对应图中的343.75Hz,以及它的2倍倍频成分687.50Hz。上述峰值较小反映齿轮工作状态良好。
由于交流电产生的工频信号为 50Hz,图中50.89Hz、50.76 Hz、101.56Hz、150.72Hz、201.34Hz、250.00Hz、300.78Hz分别约为工频的 1~6倍,这些信号是电磁干扰信号。
不同工作压力下的故障磨头的功率谱在2Hz处均有较大峰值,约等于凸轮与滚轮的冲击频率,反映凸轮与滚轮的冲击振动是磨头的主要故障源。经过对磨头进行解体检查发现,凸轮端面与滚轮接触处形成的轨迹有一道很深的压痕,证实了凸轮摆动机构的运动存在较大的冲击[5]。
问题的症结发现以后,通过对凸轮曲线进行改进设计,同时重点对摆杆的加工工艺进行了改进,由原来的立式钻床加工改为数控机床加工,减小了摆杆的形位公差,保证了凸轮摆杆机构的装配精度[6]。改进后的抛光机磨头运行时振动和噪声大幅度降低。
4 精密抛光机磨头故障测试实验
4.1 FFT频谱分析的磨头故障诊断
随机变量的相关性是指在某一时刻点上,与其他时刻数据之间的相关性或类似度。计算x(t)在 t时刻和t+τ时刻上的自相关性,用式(2)表示,信号 的自相关函数为:
利用自相关函数能可以对被随机干扰所吞噬的周期性信号进行探测。由于随机噪声随着时差的增大,其前、后的相似程度急剧下降,且自相关函数接近于 0。表明经过一段时间的延迟,其周期特性可以反应出原始信号所包含的周期分量[7-9]。故障磨头的振动信号比新磨头的信号要强烈得多。在时域中新磨头的振动讯号为正负对称,没有出现任何低频率成分。而故障磨头则出现正反不均匀性,具有很大的冲击力,但呈现出梳齿形状,能看到低频信号成分,见图2(a)、(b)和图3(a)、(b)。
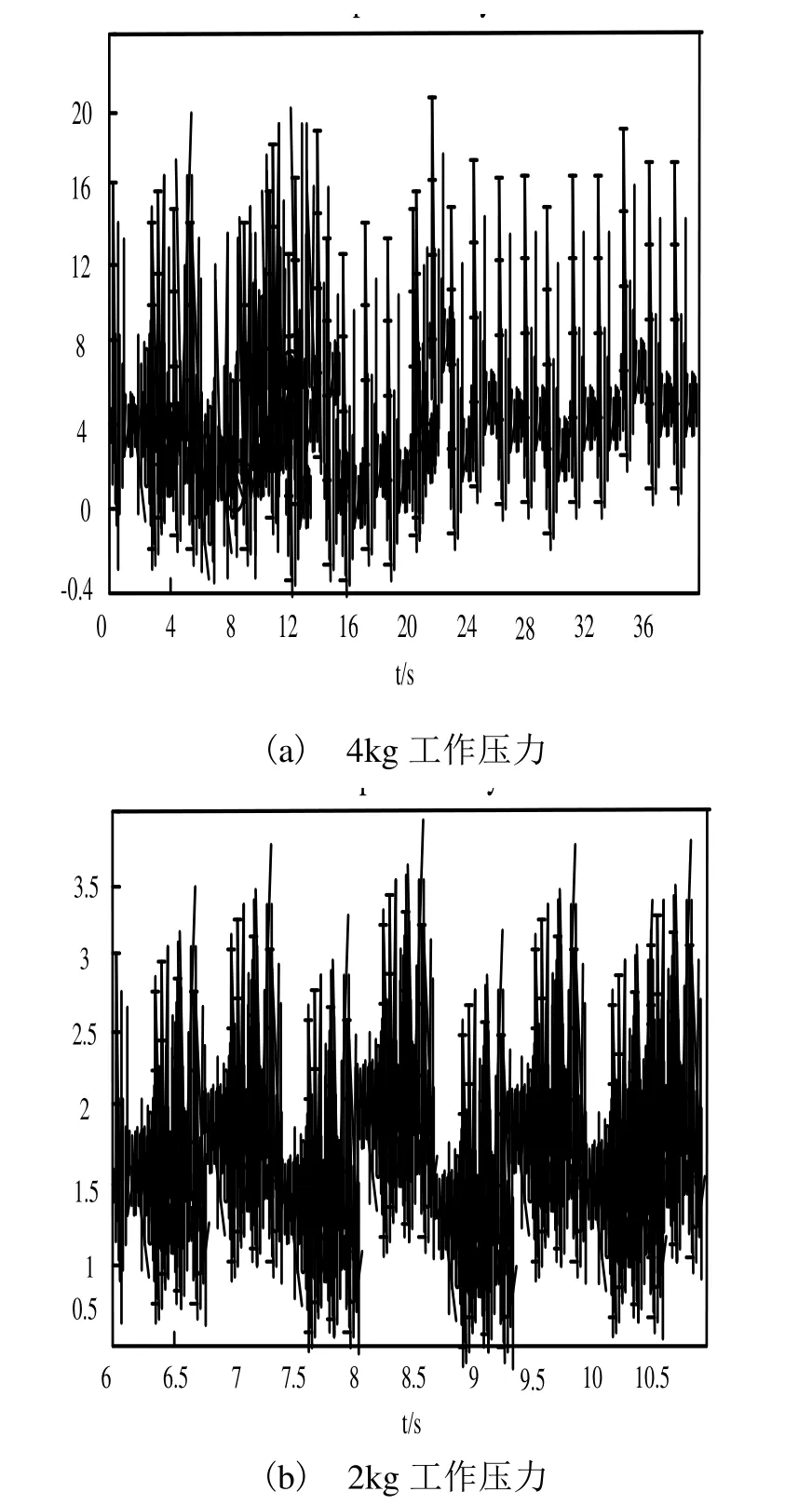
图2 故障磨头水平方向时域波形图
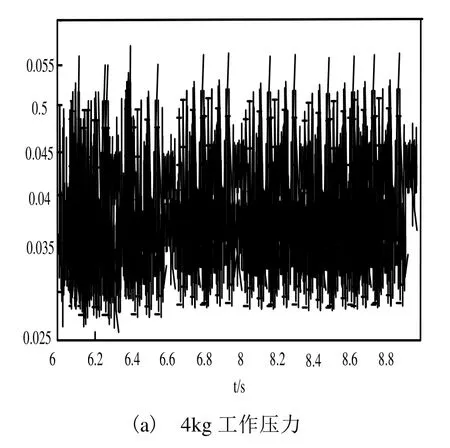

图3 新磨头水平方向时域波形图
由图2、图3可知,在相同采样频率下(8kHz),新磨头水平方向的时域波形图稳定性较高,波动较小;而存在故障的磨头水平方向的时域波形却存在很大波动;由此可知,通过时域波形图可确定磨头是否存在故障。
故障磨头的自相关函数曲线如图4(a)、(b)所示,新磨头的自相关函数曲线如图5(a)、(b)所示。
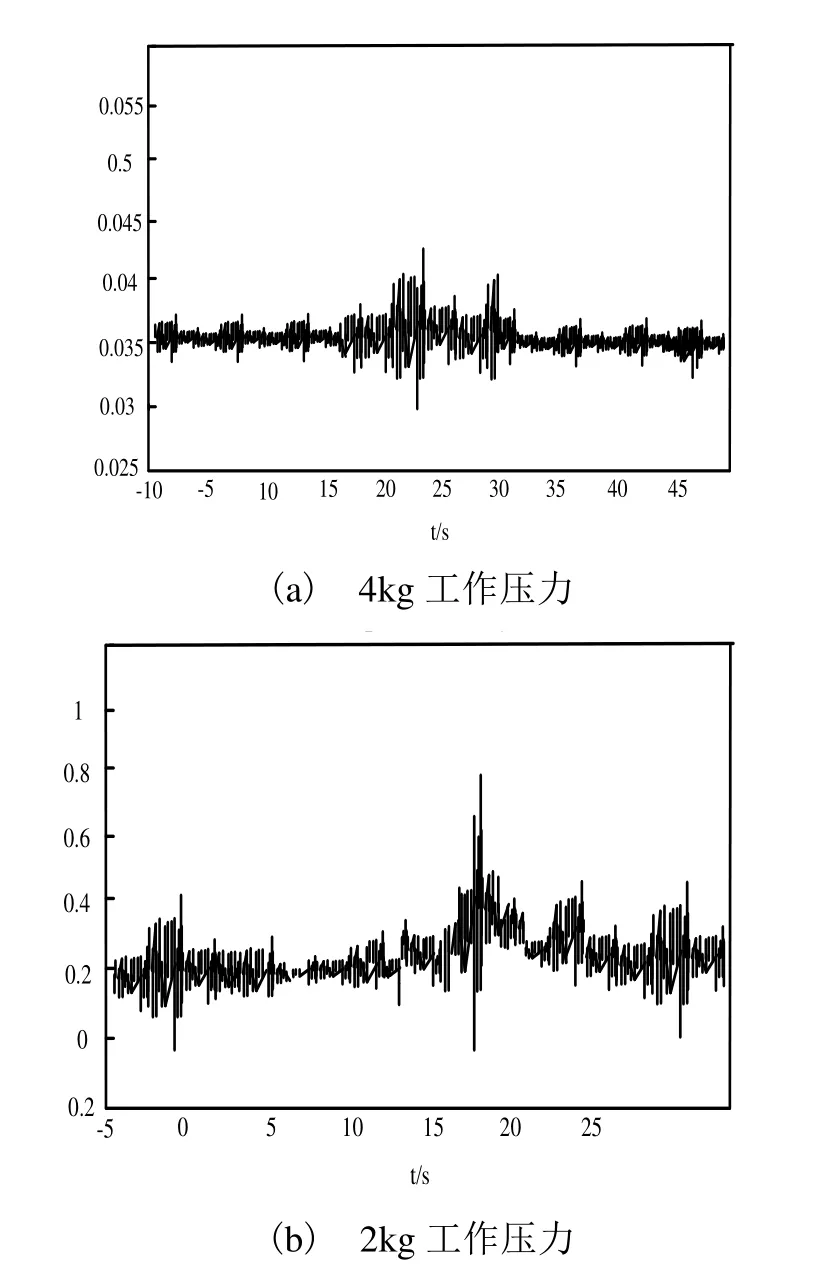
图4 故障磨头垂直方向的自相关函数曲线
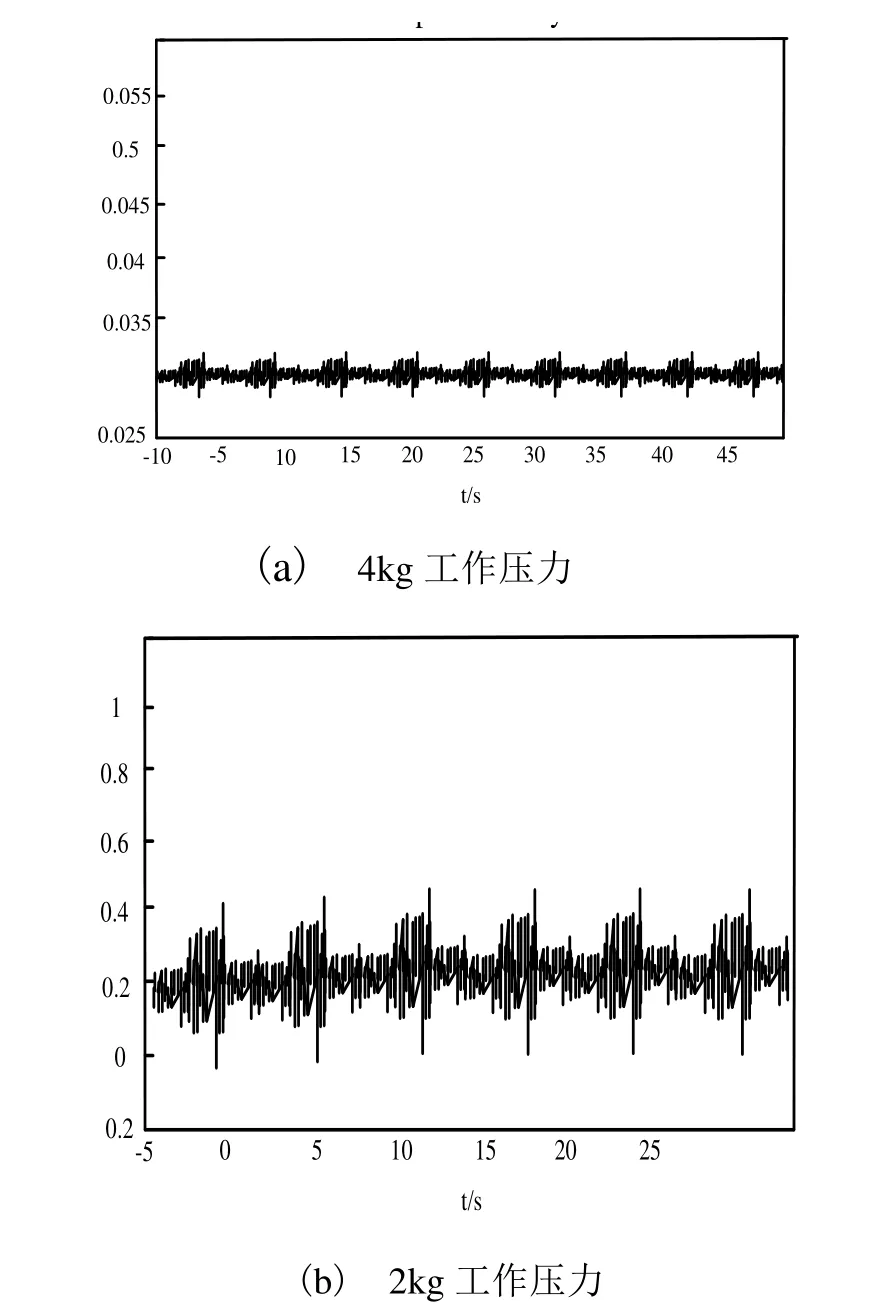
图5 新磨头垂直方向的自相关函数曲线
通过图4、图5对故障磨头的自相关曲线进行分析,发现信号特征具有显著的周期性成分,而新磨头的周期成分并不显著,表明新磨头表面光滑不存在故障时其函数曲线稳定。
由故障磨头的自相关函数曲线图可知,在各种工作压力下,其低频分量为2 Hz,而新磨头的自相关函数曲线仅含有电磁干扰信号,且多为50 Hz及其1~7倍的倍频成分,没有低频率分量[10]。
3.2 小波分析的磨头故障诊断
函数ψ(t) 作为基本小波或者母小波位移至b之后,a 作为不同尺度,f(t) 为待分析信号,将a与f(t)做内积即为小波变换的含义。
基本小波ψ(t) 是满足条件
的平方可积函数,即ψ(t)∊L2(R) 。
由函数ψ(t) 经伸缩和平移得到一族函数
a,b为实数,且a≠0
在方程式中,a为伸缩系数或尺度系数,在工程实践中,尺度系数a小于0没有任何意义;b为可正可负值的平移系数。
式(3)中参数a和参数b可根据应用的范围来确定。
设f(t)∈L2(R) 是一个能量有限的信号,其小波变换定义为f(t) 与小波函数族ψab(t) 的内积,即
式中, t是一个连续变量,同时a和b也是一个连续变量,所以把它叫做小波转换。(continuous wavelet transform,简记为CWT)
尺度因素a 的作用在于将基本小波或母小波ψ(t)伸缩处理,尺度因素越大,则越宽,与幅值成反比例缩小,其时域的分别率提高,这种特点使小波分析具有独特的应用前景。因而,可以将函数的连续小波转换可解释为对函数进行带通滤波,利用多分辨特性描述信号的局部特性,适用于对普通信号的非平稳突变进行探测。
要准确地显示出信号的特征成分,就需要选取适当的基小波,本文利用Daubechies族小波、haar小波等几个不同的小波进行了试验,结果表明,db3小波函数是最适用于对磨头故障分析的方法。
对于图2(b)所示磨头故障信号时域波形进行重新采样,采样频率1kHz,选择具有近似对称性且消失矩阶数为 3的 Daubechies3(db3)正交小波,利用多分辨分析理论进行多尺度分解。分解层数为6,各层的频率范围为 d1:500Hz~1000Hz;d2:250Hz~500Hz;d3:125Hz~250Hz;d4:62.5Hz~125Hz;d5:31.25Hz~62.5Hz;d6:15.625Hz~31.25Hz;a7:0~15.625Hz。
它们满足的运算关系为:
f(t)=a6+b6+d5+d4+d3+d1 ,其中f(t)为被分解的信号。对于分析信号中的噪声信号,其小波变换越在高频尺度层,其幅值越大,越在低频尺度层,其幅值越小。
在被测的信号中,其小波转换在较高的频率范围内,其振幅愈大,而在较低的频率范围内则愈小。表1为每一层次的分解图形的解析。

表1 6层db3小波分解波形图貌分析
为提取故障的特征频率,对第1级信号做希尔伯特转换并进行光谱解析,其结果见图6和图7。可以清楚地看到由于故障而产生的倍频和谐波信号,并且2Hz的频率被精确地抽取如从图7所示。通过对磨头的拆分检验,可以看出在凸轮与滚轮接触点上产生了一条很深的凹槽,证明该凸轮振动的振动确实很大。
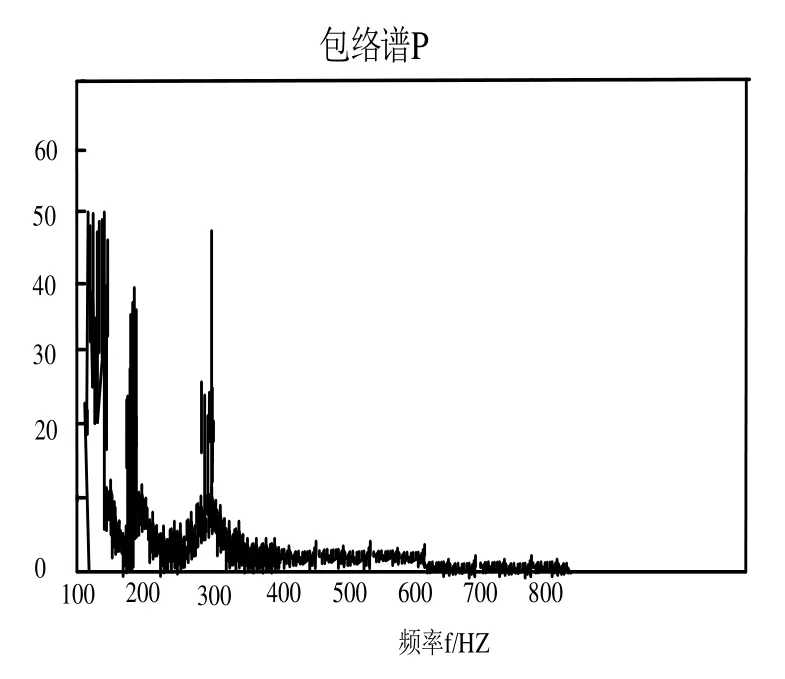
图6 第1层信号的包络谱
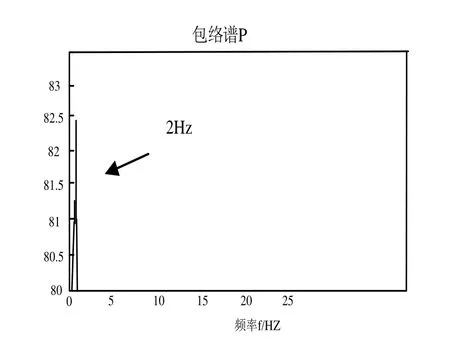
图7 第1层信号的包络谱低频段放大
4 结语
利用FFT进行的自相关分析可以直接地识别出故障的低频成分,而小波分析则可以识别出瞬态突变的信号,并显示出它的成份特征。通过两种方法对抛光机磨头故障的分析,得出与理论计算值、故障磨头的故障检测结果相符的结果。以上所提出的方法可以较精确地对平面抛光机的磨头进行故障分析。

