考虑外协服务的车辆路径优化问题

葛显龙, 宋纯冰

(1.重庆交通大学 经济与管理学院,重庆 400074; 2.重庆交通大学 智能物流网络重庆市重点实验室,重庆 400074)

0 引言

近年来，许多线下零售企业纷纷开始发展其线上零售业务，如永辉生活，重百优选等，但传统零售商如何实现线上业务与线下配送的融合，提供具有成本效益的送货上门服务，是传统零售企业转型的关键。沃尔玛和亚马逊等企业提出的一个新的解决方案是“众包”，即吸引普通人在前往目的地的路途中协助运输包裹。因此考虑使用外协服务来解决“最后一公里”配送具有重要的现实意义。

考虑外协服务的车辆路径问题的基础是将配送服务外包给具有承运能力的线下客户，这与众包配送研究息息相关。赵兴龙[1]以众包配送网络为研究对象，研究了众包配送网络中存在的延时配送和无人接单问题。随着新零售与即时物流概念的兴起，杨晓莉[2]从众包物流公司收益和客户满意度角度，对配送型众包物流的人货供需匹配进行深入研究，提出了一种定价与匹配相关联的模型。Savelsbergh和Van Woensel[3]证实了众包配送中的主要挑战是确定找到车辆出发的最佳时机以及车辆之间包裹的最佳分配比的策略。Agatz等[4]系统地概述了开发乘车共享技术时出现的优化挑战和相关的运筹学模型。Furuhata等[5]提出了一个用于了解现有拼车系统中关键因素的分类。Lee和Savelsbergh[6]对外协配送问题建立了整数规划模型，并提出启发式算法求解。Stiglic等[7]探讨了使用集合点来改善乘车共享系统性能的优点。Baldacci等[8]提出了一种用于求解拼车问题的基于列生成的精确解方法。Masson等[9]讨论了人与货物之间的运输资源共享。Li等[10]研究了出租车与乘客共同运送包裹的情景。Ghilas等[11]和Masson等[12]探讨了货运中使用公共交通的可能性及潜在优势。Fatnassi等[13]在城市物流自动化运输系统背景下研究了客运和货运的整合。Archetti等[14]研究了沃尔玛公司的愿景，并将其称为偶然驾驶员的路线问题。

以上文献分析了共享运输资源的研究情况，且多数研究都倾向于客运。与本文研究类似的Archetti等[14]考虑了使用临时驾驶员补充传统配送服务，但该学者研究的问题中没有考虑时间窗的设置。在考虑时间窗和城市配送的车辆路径问题中，葛显龙等[16,17]研究了电商企业的“自建物流+第三方物流”配送模式，建立了基于第三方软时间窗约束的车辆路径模型，并设计相应的求解算法进行求解。

因此，本文考虑使用外协服务来补充传统配送服务，建立带时间窗的车辆路径问题模型(VRPTWOS，Vehicle Routing Problems with Time Windows and Outsourced Services)，运用匈牙利算法加混合遗传算子的模拟退火算法对模型进行求解。最后结合算例对本文提出的模型与算法进行了检验与分析。

1 问题描述

考虑外协服务的车辆路径问题主要针对具有线上、线下销售同时具有物流配送服务的大型零售企业，如大型连锁超市。超市具有线下到店客户与线上客户两种，且超市意愿使用线下客户来协助完成线上客户订单的配送，未能由协作车辆服务的线上客户将由普通车辆完成配送。将协助配送的线下客户称为协作车辆，超市日常用于配送的车辆称为普通车辆。

每个线上客户具有需求和时间窗要求，违反时间窗配送将产生惩罚成本，惩罚成本与早到或迟到的时间长度成正比。假设所有协作车辆都在商店内表明其协作配送意愿，因此，所有协作车辆的起点为商店。协作车辆最多可以向客户完成一次交付，并且协作车辆在接受服务线上客户的订单时需符合自己的出行时间，因此协作车辆的交付完全符合线上客户的时间窗要求。当协作车辆与线上客户订单未能匹配成功时，其路径如图1(a)所示，该客户需要由普通车辆完成配送。当协作车辆与线上客户订单匹配成功时，其路径如图1(b)所示，协作车辆从超市完成线上客户订单后不用返回超市。

客户需求必须由普通车辆或协作车辆服务。由协作车辆服务的行程包括从超市行驶到线上客户的需求位置，以及由客户的位置到协作车辆的目的地。采取Archetti等[14]对临时司机的补偿，协作车辆收到pif=ρdoi的补偿，ρ表示协作车辆的运输补偿系数，且0<ρ<1。当不考虑临时驾驶员时，问题简化为标准的带时间窗的容量车辆路径问题(CVRPTW)。

图1 协作车辆与线上客户匹配示意图

2 建立数学模型

2.1 符号说明

2.2 协作车辆与线上客户订单匹配

首先考虑协作车辆的出行时间与客户时间窗的关系。协作车辆的服务时间满足线上客户时间窗，如式(1)、(2)所示。同时还需使协作车辆在完成服务后返回其目的地的时间不晚于其能接受的最晚时间，如式(3)所示。

af+toi≥ai

(1)

af+toi≤bi

(2)

af+toi+diNj≤bf

(3)

协作车辆接受的绕行距离最大为从超市到协作车辆目的地距离的δ倍，其中δ表示协作车辆的协作灵活度，且δ≥1，如式(4)所示。

doi+diNf≤δdoNf

(4)

ωif≤βif,∀i∈NC,f∈F

(5)

(6)

ωif∈0,1,∀i∈NC,f∈F

(7)

βif∈0,1,∀i∈NC,f∈F

(8)

式(5)表示确保将线上客户分配给愿意为该客户提供服务的协作车辆。式(6)确保协作车辆最多只能为一个线上客户提供服务。由此可得到协作车辆与线上客户订单匹配的结果。式(7)、式(8)为0-1变量。

2.3 建立VRRTWOS数学模型

根据上述分析，建立VRPTWOS问题的数学模型。

(24)

目标函数(9)为最小化总成本，包括普通车辆的路径成本、使用成本、软时间窗惩罚成本以及协作车辆的补贴成本。约束(10)表示普通车辆流量平衡。约束(11)保证普通车辆路线以超市为起止点。约束(12)表示每个需求点只能被普通车辆服务一次。约束(13)确保满足客户需求。约束(14)为普通车辆的容量约束。约束(15)保证普通车辆必须空载回到配送中心。约束(16)表示每辆普通车辆服务的线上客户数量不能超过总的线上客户数量。约束(17)为计算普通车辆行驶时间公式。约束(18)表示普通车辆离开客户点的时间与到达时间，服务时间之间的关系。约束(19)为普通车辆行驶时间计算。约束(20)表示普通车辆违背软时间窗的惩罚成本。约束(21)确保每个客户都只被服务一次。约束(22)～(24)为0-1变量。

3 算法设计

考虑到模型的特殊性，设计的算法分为两部分。第一部分完成协作车辆与线上订单的匹配。第二部分对于剩余未能匹配的线上客户订单，问题简化为带软时间窗的车辆路径问题，设计带遗传算子的混合模拟退火算法求解，模拟退火算法鲁棒性强，适合并行处理，结合遗传算子能够提高算法全局搜索能力和收敛速率。

3.1 编码设计

采用自然数编码方式表示方案的解，以客户编号作为解的元素，0作为配送中心。每个解可分为几条路线，必须包含所有客户点，每条路线包含配送中心和至少一个客户点，解的路线之间由配送中心0隔开。

3.2 设计协作车辆与线上订单的匹配算法

步骤1利用协作车辆的出行时间与客户允许的时间窗服务时间进行初步匹配。

步骤2筛选符合距离约束的结果。

步骤3使用匈牙利算法，得到每个协作车辆服务一个线上客户的同时总成本最小的匹配结果。

步骤4将成功匹配的线上客户订单从线上客户订单列表中删除。

3.3 设计混合模拟退火算法

(1)初始解的生成

步骤1对于未被成功匹配的线上客户订单，使用节约里程算法，在不考虑容量约束的前提下生成超市到线上客户点的TSP解。即只有一辆普通车辆从超市出发服务所有的未被成功匹配的线上客户后返回超市。

步骤2判断路线上的线上客户需求是否符合普通车辆的容量约束，超出容量限制则通过分车算子拆分为两条路径。

步骤3对于符合普通车辆容量约束的线路，判断普通车辆到达线上客户点的时间是否在规定的时间窗约束内，若满足则生成初始可行路径。

(2)设计遗传算子

选择算子采用传统轮盘赌算子。

交叉算子采用保留最佳子串策略。任选两条染色体作为父代1和父代2，保留父代1中载重量最大的子串，并将其作为选中基因提前，同时选择父代1中除超市外的另外两个随机基因作为固定基因，并将选择基因和固定基因以外的基因剔除。将父代2中与上述未被剔除基因相同的部分剔除，并将父代2中剩余除超市外的基因依次插入父代1中。按照规定的容量约束重新插入超市。

变异算子为随机选择一条染色体，在该染色体中随机选择一个变异位置，若该位置不为0，则随机生成一个新基因替换原有基因。若变异位置基因为0，则重新选择变异位置。

(3)设计模拟退火扰动算子

模拟退火算法中采用随机扰动算子，其步骤如下表示

步骤1产生新状态sj=Genete(s);

步骤2ifmin{1,exp[(-C(sj)-C(s))]}≥random[0,1),s=sj;

步骤3min{1,exp(-ΔC/t)}作为状态函数接受准则。

4 算例分析与仿真

4.1 实例仿真

以重庆某零售超市及其周边117个小区为例，超市D00为配送中心，C1-C67表示线上客户，F1-F50表示线下客户的目的地。线上客户的需求及时间窗已知，见附件中表1，线下客户的出行时间已知，如附件中表2所示。

为验证在实际情况中使用外协服务可以带来何种程度的成本节约，在补偿系数ρ=0.1，协作灵活度δ=1.5，即在高协作灵活度，适中补偿系数下进行测算，假设普通车辆容量为100件，普通车辆启动成本200元，两种车辆的单位运输成本均为5元，普通车辆违背时间窗单位惩罚成本为2元，两种车辆的行驶速度均为30公里/小时的情况下，对VRPTW和VRPTWOS成本分别进行10次测算。

表1 参数灵敏度分析

测算结果显示，使用外协服务可以有效降低总成本。在不使用外协服务时，平均成本为1716.055元，需使用7辆普通车辆来完成全部67个线上客户订单。在考虑使用外协服务时，有23个线上客户订单可以由协作车辆服务，只需5辆普通车辆完成剩余44个线上客户订单，总配送成本为1298.7元。在3次测试中，平均成本节约为24.32%，普通车辆使用数减少28.57%。为验证在不同补偿系数以及不同协作灵活度的情况下对结果的影响，使用补偿系数ρ=0.05,0.1,0.2和协作灵活度δ=1.1,1.3,1.5的多种可能组合对实例求解，结果如表1所示。

由表1可知，协作灵活度越大时，即协作车辆可以接受配送的范围越广时，总配送成本越低，同时当协作灵活度增大时，协作车辆与线上客户订单的匹配程度增加，在一定程度上减少普通车辆的使用。同时随着补偿系数的增大，总配送成本的降低越小。经过测算，当ρ=0.3时，在低协作灵活度的情况下已经无法降低总配送成本。

图2为使用混合遗传算子的模拟退火算法得到的不考虑外协服务时的实际普通车辆运行路线。

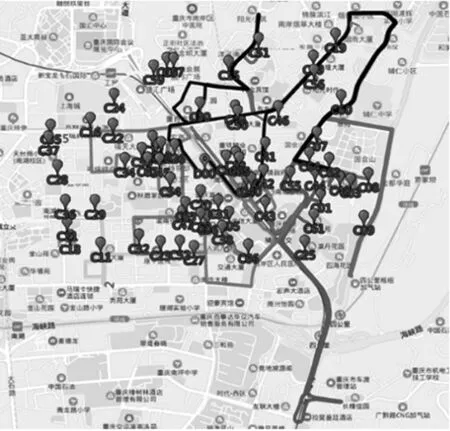
图2 不考虑外协服务时的实际普通车辆运行路线

在考虑外协服务时对未能成功匹配的客户重新编号为1- 44，使用混合遗传算子的模拟退火算法求解得到普通车辆路径解，在百度地图中得实际运行线路如图3所示。

图3 考虑外协服务时的普通车辆实际运行路线

由图2、图3可以看出，考虑使用外协服务时的实际运输距离要少于不使用外协服务时，并且线路数也有所减少。由于南坪商圈的实际交通道路错综复杂，存在单行道、隧道、立交等特殊情况，因此在实际车辆运行路线中存在绕行的情况。同时由于客户包含时间窗需求，所以在实际的运行线路图中存在线路重叠。

4.2 算例分析

为了验证算法的有效性，本文进行了算例的分析验证。我们从Solomon算例中选取了三种不同客户分布的实例来进行验证，并在算例中随机选择50个客户作为线下自提客户，其余50个作为线上客户。在补偿系数ρ=0.1,δ=1.5，普通车辆的最大装载为100件，普通车辆启动成本200元，普通车辆和协作车辆的单位运输成本均为5元，普通车辆违背时间窗单位惩罚成本为2元，普通车辆和协作车辆的行驶速度均为30公里/小时的情况下对算例进行了测算，具体结果如表2所示。

从结果可以看出，我们的匹配方式可以实现最高66%的匹配率，平均匹配率可达42%，证明了我们的匹配方式的可行性。表6显示，使用线下客户外协服务可以带来最多54.76%的成本节约，平均的成本节约为34.01%，同时可以带来平均38.06%的车辆使用数的减少。从而证明了我们算法的有效性。

为进一步验证本文算法的有效性，将混合遗传算子的模拟退火算法分别于遗传算法和模拟退火算法进行性能对比，以67个线上客户位置节点为例，分别在不考虑外协服务时和考虑外协服务时进行验证，运算结果如表3所示。

经过测算，在不考虑外协服务时，三种算法均使用7辆普通车辆完成67个线上客户点的运输，混合模拟退火算法得到的平均解和最优解均优于遗传算法和模拟退火算法。混合遗传算子的模拟退火算法得到的平均解比遗传算法成本节约了6.31%，对比模拟退火算法成本节约了3.61%。

在考虑外协服务时，由于匹配算法相同，在同种情况下协作车辆的匹配率相同，均为存在23个线上客户由协作车辆完成配送。三种算法均使用5辆普通车辆完成剩余线上客户订单的配送。此时混合遗传算子的模拟退火算法取得的最优解和平均解依然由于遗传算法和模拟退火算法。混合遗传算子的混合遗传算子的模拟退火算法得到的平均解比遗传算法成本节约了5.41%，对比模拟退火算法成本节约了2.59%。由此可得，本文设计的算法在寻优能力上优于遗传算法与模拟退火算法。

表2 算例测试结果

表3 不考虑外协服务时算法性能比较

5 结论

针对开展线上销售的新型零售企业的末端配送问题，引入了外协服务的概念，使用线下自提客户来协助完成部分线上客户订单的配送，建立了考虑外协服务的最小化总成本的数学模型，并使用混合遗传算子的模拟退火算法进行求解，最后结合算例分析得出了以下结论：(1)针对协作车辆与线上客户的匹配设计了匹配算法，可以得到平均为42%的匹配成功率。(2)使用外协服务来解决相对应的配送问题可以在一定程度上降低配送成本和减少普通车辆的使用。

本文研究的目的是对使用外协服务来解决实际配送问题提供初步探讨。对于未来的研究，可以关注协助车辆的不同停车意愿对于总配送成本的影响，也可将连锁零售超市看作多个配送中心的车辆路径问题来进行新的探讨。在后续的研究中会继续考虑和关注这两个方面。