利用高性能混合深度学习网络提升光谱分类性能研究
刘忠宝,王 杰
1.北京语言大学信息科学学院,北京 100083 2.中国科学院新疆天文台,新疆 乌鲁木齐 830011
引 言
随着海量光谱数据的不断涌入,如何进一步提高光谱分类性能引入广泛关注。目前,国内外有关恒星光谱分类的研究已有不少成果。Daniel等探讨了降维技术在恒星光谱分类中的有效性问题,他们引入局部线性嵌入技术,通过保持高维光谱数据在低维空间的局部结构,进而实现恒星光谱的自动分类[1]。Navarro等利用人工神经网络对低信噪比的恒星光谱进行分类[2]。Sanchez等试图利用k-均值聚类算法对SDSS SEGUE和SEGUE-2恒星光谱进行无监督分类[3]。鉴于传统分类方法具有较高的时间复杂度问题,Liu等受协同管理思想启发,提出非线性集成学习机,并将该模型应用于恒星光谱分类[4]。Huertas-Company等在支持向量机的基础上提出一种确定星系形态的非参数方法[5];Peng等利用支持向量机从SDSS、UKIDSS等巡天项目获得的光谱中搜寻类星体候选体[6];Malek等在VIPERS数据集上利用SVM来将恒星、活动星系核和星系区分开来[7];Brice等在SDSS数据集上利用K近邻算法和随机森林算法进行对恒星光谱进行分类[8]。
此外,越来越多的研究人员将深度学习模型用于解决恒星光谱分类问题。Liu等研究了基于一维卷积神经网络的恒星光谱分类方法[9]。王楠楠等探讨了卷积神经网络应用于恒星光谱分类的可行性问题[10]。尽管实验结果表明上述模型较之传统机器学习算法具有更优的分类效率,然而受其工作机理限制,该模型在特征提取以及特征理解方面仍存在一定差距,严重影响了该模型分类效率的进一步提升。幸运的是,BERT(bidirectional encoder representation from transformers)模型的出现为解决上述问题提供了可能。鉴于此,本工作提出高性能混合深度学习网络BERT-CNN,试图充分利用BERT模型和CNN模型在特征提取和自动分类方面的优势,以期进一步提高光谱分类性能。
1 高性能混合深度学习网络BERT-CNN
BERT-CNN模型如图1所示。该模型的工作流程为:首先,将恒星光谱数据依次输入BERT模型;然后,利用BERT模型中的Transformer(图1简写为Trm)进行特征提取,得到特征向量T1—TN;最后,在CNN模型中输入上述特征向量并自动分类,进而得到恒星光谱的分类结果。
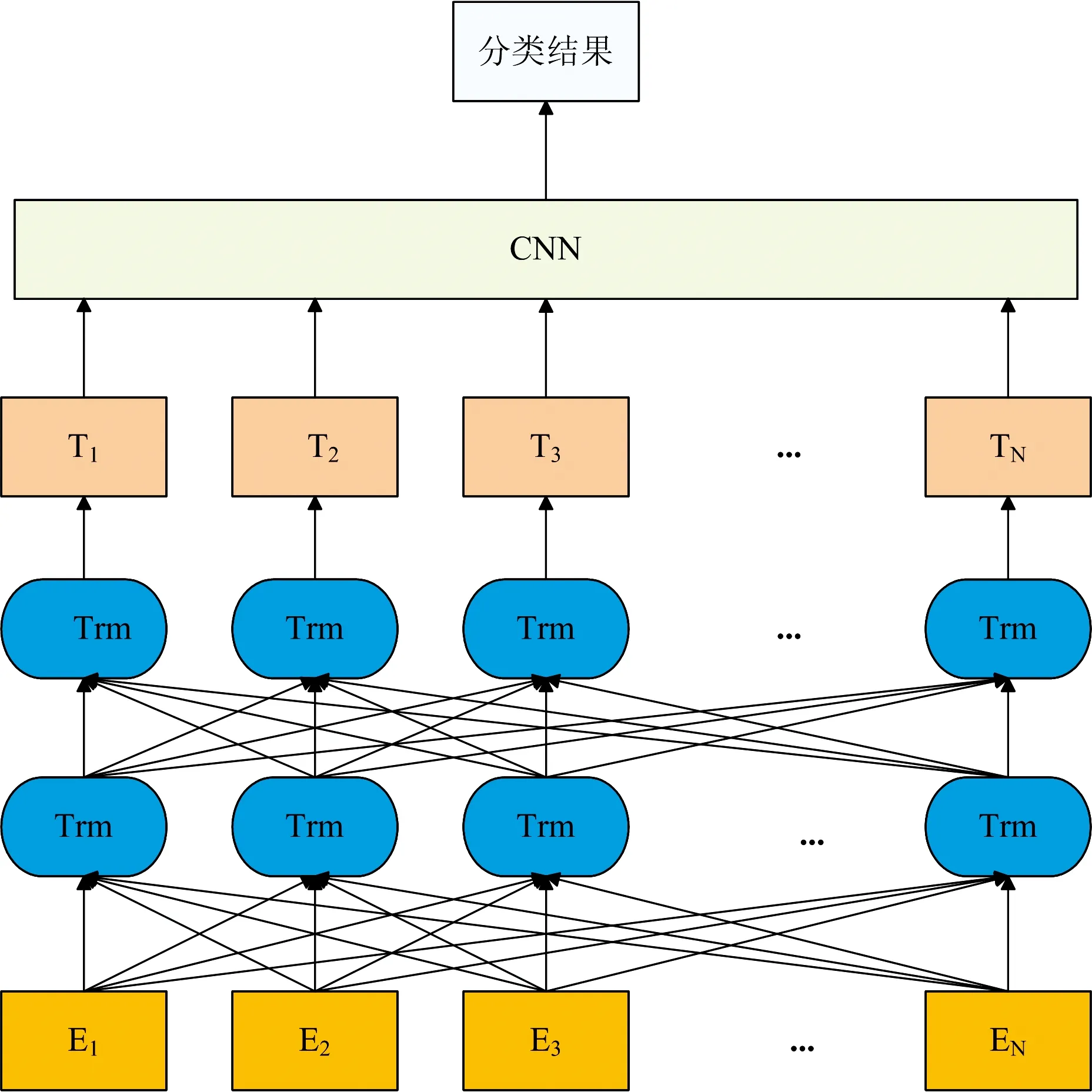
图1 BERT-CNN模型Fig.1 The structure of BERT-CNN
(1)BERT模型
BERT模型采用了多层双向Transformer编码器,能够更好地提取恒星光谱数据的深层次特征。Transformer编码器(以下简称Transformer)是BERT模型最重要的部分,其主要由多头自注意力机制和全连接前馈神经网络层两个子层组成。为了解决随着网络的加深而产生的性能退化等问题,Transformer在两个子层间加入了残差网络,并在每个子层后添加归一化层来加速模型收敛。
Transformer基于自注意力机制,该机制更易捕获光谱特征之间的内在关系。其计算过程见式(1),其中Q和K为维度为dk的Query矩阵和Key矩阵,V为维度为dv的Value矩阵。
(1)
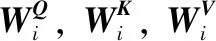
MultiHead(Q,K,V)=Concat(head1,…,headh)Wo
(2)
(3)
层归一化与前馈神经网络的计算过程见式(4)和式(5)。
(4)
FFN(x)=max(0,xW1+b1)W2+b2
(5)
式(4)中,μ和σ为输入层的均值与方差,α和β为待学习的参数,ε的取值很小;式(5)中,前馈神经网络层以修正线性单元ReLU作为激活函数,x表示网络的输入,W和b为待训练的参数。
(2)卷积神经网络
CNN模型由输入层、卷积层、池化层以及全连接层组成。输入层为恒星光谱矩阵,矩阵中的每一行向量对应一条恒星光谱。卷积层对输入向量进行卷积操作,进而生成特征向量。卷积计算见式(6)和式(7),其中l为CNN的网络层数,j为特征图,k为卷积核,bC为偏置,Nj为特征向量集合,ReLU为激活函数。
(6)
(7)
池化层的作用是压缩特征向量的规模,以期达到降低特征向量维度、减少参数规模的目的。该层经过最大池化方法保存局部信息,以期得到池化后的特征向量。在全连接层,将池化后的特征向量进行整合,最后通过softmax分类器获得分类结果。softmax分类器的表达式见式(8)。
(8)
2 实验部分
将Python3.7作为的编程语言,并使用TensorFlow1.14作为深度学习模型框架。实验数据集为SDSS DR10中的K型、F型、G型恒星光谱数据,如表1(a)—(c)所示。K型恒星包含K1,K3,K5和K7次型,而这四种次型光谱的信噪比(signal noise ratio,SNR)区间均是(60,65);F型光谱包括F2,F5和F9次型,其各次型光谱的信噪比区间分别为(50,65),(65,70),(75,80);G型光谱包括G0,G2和G5次型,其各次型信噪比区间为(55,65),(60,65),(40,70)。
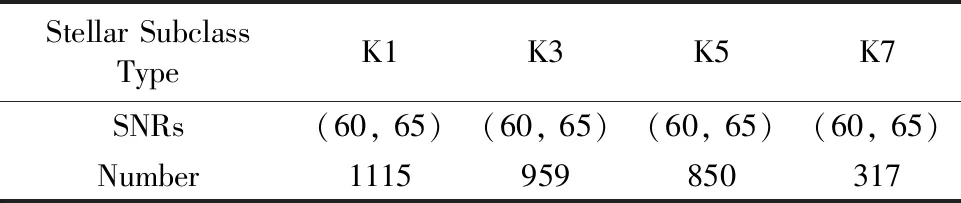
表1(a) K型恒星光谱数据集Table 1(a) The dataset of K stars

表1(b) F型恒星光谱数据集Table 1(b) The dataset of F stars

表1(c) G型恒星光谱数据集Table 1(c) The dataset of G stars
采用min-max标准化方法对恒星光谱数据进行归一化处理,该方法通过对恒星光谱数据进行线性变换,使原始光谱数据保持在[0,1]区间。其计算公式为
其中,xNorm表示恒星光谱数据归一化后的特征值,x表示原始恒星光谱数据,xmax和xmin分别表示每条恒星光谱数据的最大值和最小值。
通过与SVM、CNN等分类模型的比较来验证所提模型的有效性。引入网格搜索以及10折交叉验证来得到模型的实验参数。在SVM模型中,在网格{0.01,0.05,0.1,0.5,1,5,10}中搜索惩罚因子的最优取值,多次实验表明,当惩罚因子等于0.1时,模型的性能最优。在CNN模型和BERT+CNN混合模型中,batch_size表示一次训练选取的样本数,learning_rate表示模型的学习率大小,两者均在网格{1×10-2,1×10-3,5×10-4,1×10-4,5×10-5,2×10-5,1×10-5}中选取;hidden_units表示隐藏层神经元数,在网格{64,128,256,512,1 024}中选取;dropout为丢弃率,在网格{0.1,0.2,0.4,0.5,0.6,0.8}中选取。表2给出了CNN、BERT-CNN等模型的实验参数设置。
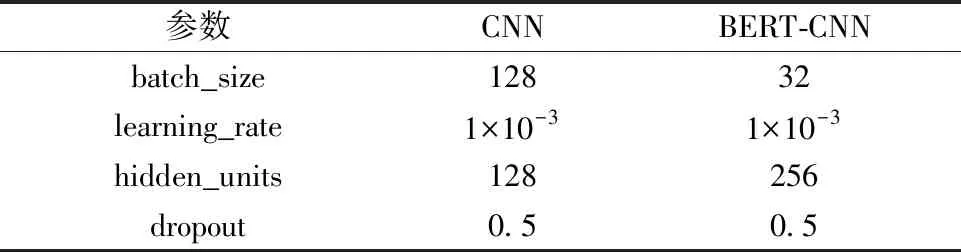
表2 CNN,BERT-CNN模型参数设置表Figure 2 The parameters of CNN and BERT-CNN
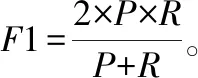
当训练数据集占比实验数据集的30%~70%且剩余数据集为测试数据集时,BERT-CNN模型的实验结果如表3(a)—(c)所示,其中括号前的值表示实验数据规模,括号中的值表示占比。
由表3(a)—(c)可以看出,BERT-CNN模型的精准率P、召回率R、调和平均值F1随训练样本数的增加而提升。在相同规模的训练样本条件下,BERT-CNN模型在K型数据集上的P,R和F1值均最高,其次是G型数据集,F型数据集上的分类效果较差。当训练样本数占比大于等于50%时,三类数据集上的P,R和F1值均超过0.91,这表明BERT-CNN模型适用于解决恒星光谱分类问题。
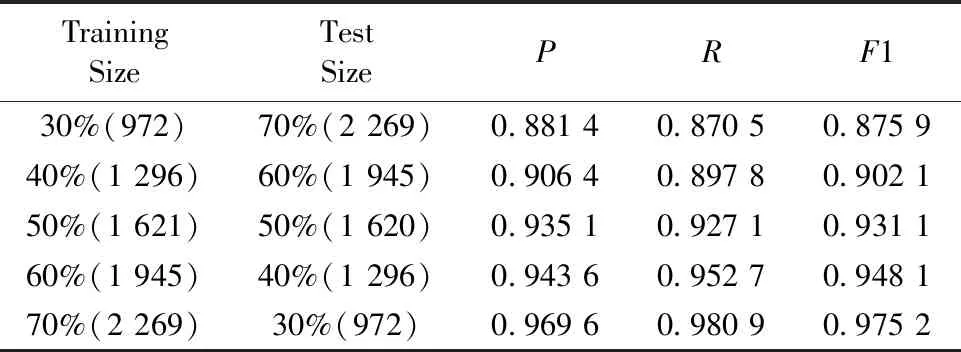
表3(a) BERT-CNN模型在K型恒星数据集上的实验结果Table 3(a) The experimental results of BERT-CNN on the K-type dataset
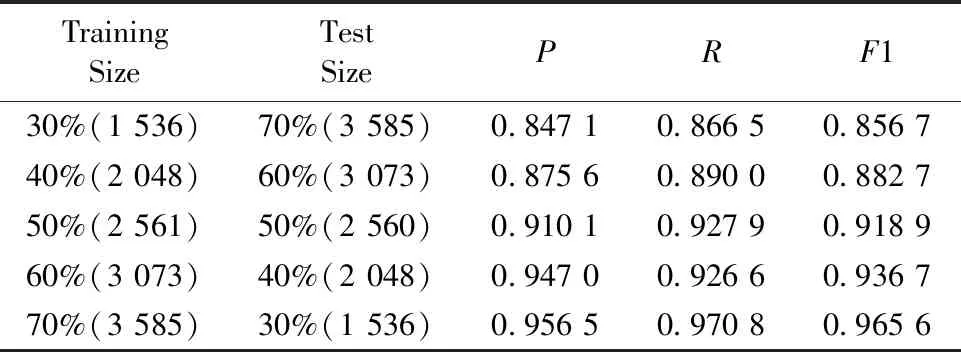
表3(b) BERT-CNN模型在F型恒星数据集上的实验结果Table 3(b) The experimental results of BERT-CNN on the F-type dataset
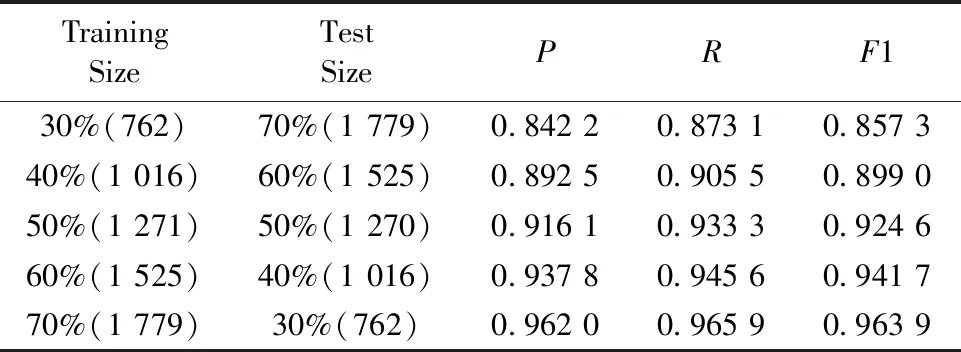
表3(c) BERT-CNN模型在G型恒星数据集上的实验结果Table 3(c) The experimental results of BERT-CNN on the G-type dataset
三类模型的对比实验结果由准确率A来评价,准确率是正确分类光谱数与总体测试光谱数的比值。实验数据集的70%作为训练数据集,剩余数据集作为测试数据集,实验结果如表4所示。
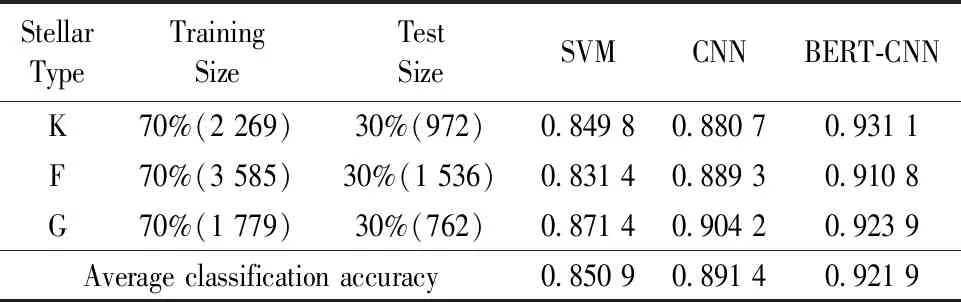
表4 实验结果比较Table 4 Comparison of experimental results
由表4可以看出,BERT-CNN模型分类效果最优,其次是CNN模型,最后是SVM模型。具体而言,在K型数据集上,BERT-CNN模型比SVM模型的准确率高0.081 3,比CNN模型高0.050 4;在F型数据集上,BERT-CNN模型比SVM模型的准确率高0.079 4,比CNN模型高0.021 5;在G型数据集上,BERT-CNN模型比SVM模型的准确率高0.052 5,比CNN模型高0.019 7。此外,BERT-CNN模型的平均准确率均最高。这表明,BERT-CNN模型具有更优的光谱分类性能。
3 结 论
为了进一步提高以CNN模型为代表的深度学习模型恒星光谱分类效率,以恒星光谱为研究对象,充分利用BERT模型和CNN模型在特征提取和自动分类方面的优势,提出高性能混合深度学习网络BERT-CNN。SDSS数据集上的实验结果表明,所提模型有助于提升恒星光谱分类性能。上述结论在其他类型光谱上是否成立有待于进一步研究。

