基于WOA-SOS的无线传感器网络节点定位

傅 彬

（绍兴职业技术学院，浙江 绍兴 312000）

0 引 言

随着5G通信技术的快速发展，物联网（Internet of Things，IoT）技术[1]已经成为当前信息技术发展的新的组成部分。无线传感网络（Wireless Sensor Network，WSN）作为物联网中一种重要的应用技术发挥着举足轻重的作用。在实际场景的应用中，节点定位技术是WSN的重要基础，这是因为无线传感网络中的节点在获得准确的信息后，才能将自身携带的数据进行发送和接收，才能使所携带的数据发挥最大的应用价值。因此，如何获得节点的精确位置以及提高定位精度，已经成为WSN研究的焦点。文献[2]提出了基于斯蒂芬森迭代改进DVHop的无线传感器节点定位算法，仿真实验说明该算法相比于改进前的算法无论是在未知节点的定位时间上，还是在节点的定位准确率上都有明显的提升，但缺乏与较新定位算法的对比。文献[3]提出了一种改进樽海鞘群算法优化的DV-Hop定位算法，算法的定位精度较高，具有更好的定位能力，但算法的复杂度有所提升，提高了节点能耗。文献[4]提出一种基于改进粒子群算法优化LSSVR模型的定位方法，在定位效果方面具有较好的稳定性与实时性。文献[5]提出一种改进的人工免疫算法（AIA）优化DV-Hop未知节点坐标，具有较高的定位精度和较好的定位稳定性，同时也改善了算法的收敛性，但缺乏与更多算法效果的对比，实验效果有待进一步验证。文献[6]提出了改进的加权质心算法节点定位方法，仿真实验说明该算法相较传统质心算法具有定位精度高、用时少等优势，但缺乏与其他优化后的质心算法的对比。文献[7]提出基于反向学习的群居蜘蛛优化WSN节点定位算法，该算法收敛速度更快，节点定位精度更高，但提高了算法的复杂度，影响了节点定位时间。文献[8]提出了基于量子退火算法的无线传感器网络节点定位方法，该方法相比于传统的遗传算法和模拟退火算法来说，在定位精度和节点定位能耗上都有显著的提升；文献[9]提出了一种基于灰狼算法的节点定位模型，该模型使用灰狼算法优化DV-HOP算法中的节点位置，仿真实验说明该算法在节点定位中的指标获得较好的结果。文献[10]提出了一种基于butterfly optimization algorithm的节点定位算法，仿真实验说明该算法能够改善节点的定位效果。文献[11]提出了基于优化的粒子群的混合算法用于节点定位，仿真说明优化后的算法定位效果相比于单一算法具有更好的定位效果。文献[12]提出使用猫群算法用于节点定位，通过对猫群算法进行不同程度的优化，使得改进后的猫群算法在节点定位中获得了较好的效果.

在以上的研究中，学者们使用了元启发式算法用于无线传感器网络的节点定位，取得了较好的效果。本文在以上研究成果的基础上，提出了基于鲸鱼算法和生物共生演算法的融合算法（Whale Optimization Algorithm-Symbiotic Organisms Serarch，WOA-SOS）用于节点定位的研究。仿真实验说明该算法具有较好的性能，能够有效地降低节点定位误差。

1 节点定位优化函数

无线传感的定位问题本质上是一个多约束优 化 问 题[13]。设 定n（n＞3）个 锚 节 点P1(x1,y1)，P2(x2,y2)，…，Pn(xn,yn)与未知节点P(x,y)之间的实际测量距离为d1,d2,…,dn，因此表达如下：

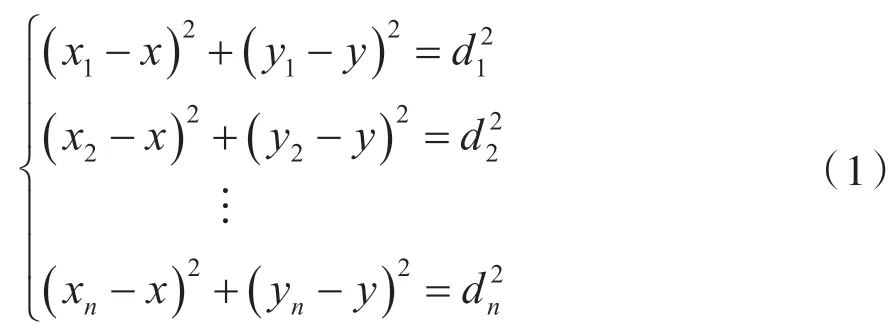
使用线性方程组表示AL=b

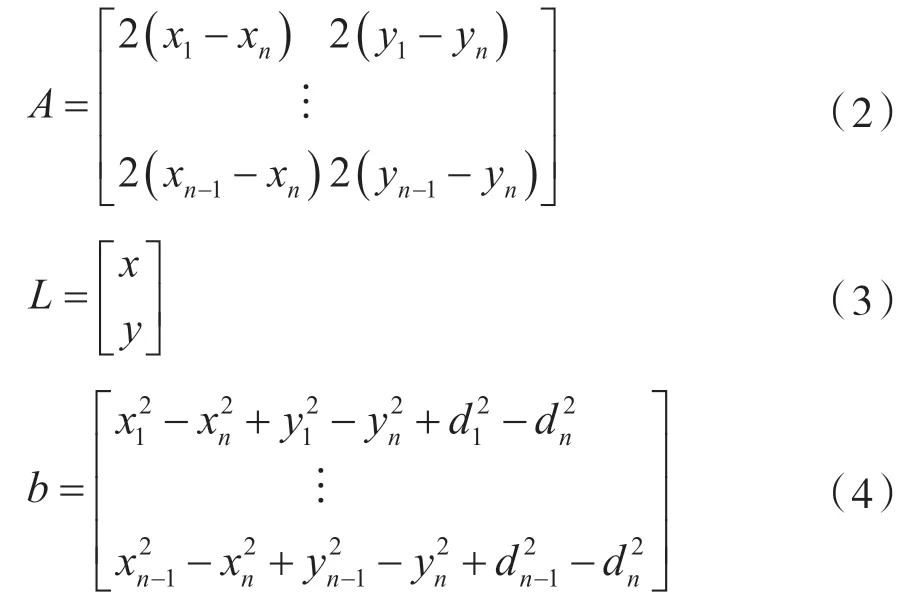
实际环境过程中肯定会存在一些误差因素ε，因此以上的线性方程组可修正为AL+ε=b，通过最小二乘法表示如下：

因此优化问题转换为如下表达：

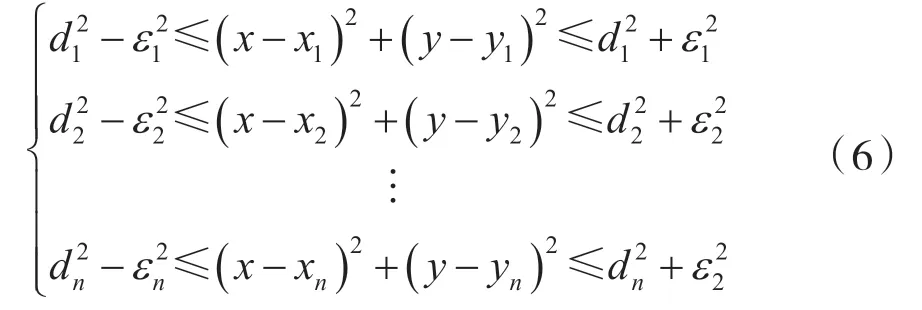
因此定义目标函数为：

通过上面的推导过程可以发现，式（6）的解在一个可行解的区域中，而处于这个可行解区域一定包含了最优解，因此，根据式（7）来计算整体上获得最小值的坐标，也就是需要求解的未知节点的坐 标(x,y)。

2 基本算法

2.1 鲸鱼算法

2016年，MIRJALILI S[14]根据鲸鱼在大海中的捕食行为提出了鲸鱼算法（Whale Optimization Algorithm，WOA）。主要分为包围捕食、气泡攻击、寻觅食物三个阶段。

2.1.1 包围捕食

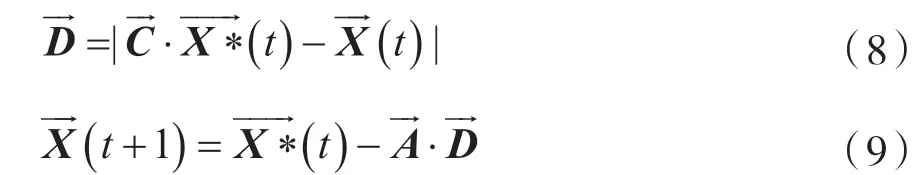
在算法的初级阶段，座头鲸将距离食物最近的鲸鱼当作当前的一个最优解，数学模型表达为：式中：表示搜索代理座头鲸到目标食物之间的距离向量，t用来表示当前算法执行的迭代次数，和分别表示系数向量，X*为当前迭代次数下的局部最优解，表示当前座头鲸的位置向量，和的表达数学公式如下：

式中：表示一个线性递减向量，其值从2到0，r表示0到1之间的随机数。

2.1.2 气泡攻击

本阶段主要阐述座头鲸进行气泡攻击，通过收缩包围和螺旋更新位置来设计鲸鱼捕食吐出气泡的行为过程，逐步达到鲸鱼局部寻优的目的。

（1）收缩包围原理

在式（9）中，当|A|＜1时，鲸鱼个体向着当前位置最优的鲸鱼靠近，并且|A|越大鲸鱼游走的步伐越大，当|A|越小，鲸鱼游走的步伐就越小。

（2）螺旋更新位置

座头鲸个体计算与当前最优鲸鱼的距离，然后再以螺旋方式游走，其数学模型公式如下：

2.1.3 寻觅食物阶段

座头鲸个体向着参考座头鲸的位置靠近，鲸鱼个体朝着随机选取的座头鲸更新位置，获得全局最优解，其数学公式模型如下：

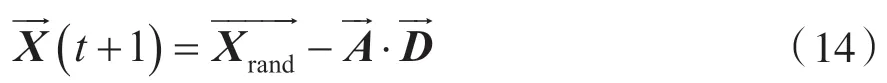
式中：Xrand是随机获得的参考座头鲸的位置向量。

2.2 共生演算法

2014年，CHENG M Y等人根据大自然中的生物生活的特性，并结合大自然规律，提出生物共生演算法（Symbiotic Organisms Serarch，SOS）[15]。该算法根据生物生活特性主要分为共生、共栖、寄生三个阶段。

（1）共生阶段。设置Xi表示第i个生物个体，Xj表示随机和Xi进行相互作用的个体。这两种Xi与Xj是基于相互共生的候选解的关系，表达如下：

式中：BF1和BF2表示相关的利益因素，Xbest代表当前解中适应度最高的个体。如果当前第i个生物个体的适应度数值高于当前适应度值最高的个体，则Xi变为Xinew，否则，Xj变为Xjnew，否则保持不变。

（2）共栖阶段。Xi产生的新候选解是根据生物Xi和Xj生物之间的共生关系来获得，表达如下：

在该阶段中，该Xi对应的个体适应度值优于适应度最高的个体，则Xi个体变为Xinew，否则保持 不变。

（3）寄生阶段。算法设定人工的寄生虫Parasite来避免算法过早地陷入过早的收敛。它的设计来源是在搜索空间中对个体Xi复制而来，设定为[0，1]之间的随机数与该生物个体Xi乘积。

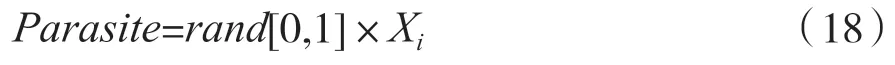
在该阶段中，算法随机选择一个生物个体Xj作为设定的人工寄生虫的载体。在算法迭代过程中，一旦这个人工寄生虫个体的适应度值优于当前最优个体，则会取代该生物个体，否则该生物个体获得进一步的免疫，从而去除人工的寄生虫Parasite，能够有效地避免算法陷入过早的收敛。

3 基于WOA-SOS算法的节点定位

类似大部分元启发式算法的特点，WOA算法同样也会存在容易陷入局部停滞、导致算法收敛速度慢、解的精度有待提升的问题。本文提出3个反面的鲸鱼算法的优化策略：（1）利用混沌映射进行种群初始化，保持种群具有多样性；（2）构建自适应权重因子改进螺旋更新位置，避免算法陷入局部最优；（3）利用生物共生演算法进行个体的更新。

3.1 种群初始化

种群的初始化在很大程度上影响着算法的效果。随机产生的初始化并无法保证种群具有的多样性，因此本文在混沌映射思想的基础上进行种群初始化，公式如下：

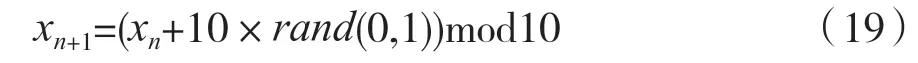
设置种群规模N、维度D和最大混沌迭代步数K，种群初始化方法具体如下：

其中，xk-1,j表示在k-1次迭代中的第j维中的第i个个体，xk,j表示采用了混沌映射后的第k次迭代中j维中的第i个个体，xi,j表示第j维中的第i个个体，xmax,j和xmin,j分别表示j维空间的上下界。

3.2 自适应收敛因子

在基本的WOA算法公式（11）发现，A值在很大程度上受到a的影响，当a值较大，算法具有较好的全局搜索能力，反之则容易陷入局部最优。因此a值就显得非常重要。因此，本文设定a值表达如下：

式中：tmax为算法设定的最大迭代次数，t表示个体在当前的迭代次数，fobj(xi)表示当前鲸鱼个体i在当前迭代次数下的适应度值。a0为初始值为1。

3.3 节点定位步骤

步骤1：将无线传感网络中的节点问题与鲸鱼个体进行一一对应，选出最优的座头鲸，就是最优的节点定位方案。将鲸鱼个体的适应度函数设定为式（7）的节点定位优化函数。

步骤2：对WOA算法设置算法的基本参数，设置迭代次数。

步骤3：采用改进的混沌映射进行种群初始化和自适应因子参数。

步骤4：在每一个迭代完成后，对个体采用共生共演算法优化，选择更优的鲸鱼个体进入下一次 迭代。

步骤5：判断迭代次数是否达到Tmax，如果达到，则算法结束，获得最优的鲸鱼个体即最好的定位效果，反之则转到步骤3。

4 算法仿真

为了更好地说明本文算法在节点定位中的效果，将实验分为两个部分展开研究。第一部分阐述本文算法（WOA-SOS）的性能，第二部分阐述本文算法在节点定位中的效果。

4.1 性能对比

本文将WOA-SOS算法和WOA算法在不同维度（2维、5维、30维）的6个基准测试函数（如 表1所示）下进行对比，算法选择各自参数并设置相同的迭代次数，借助Matlab 2012仿真平台得到仿真结果，如表2所示。

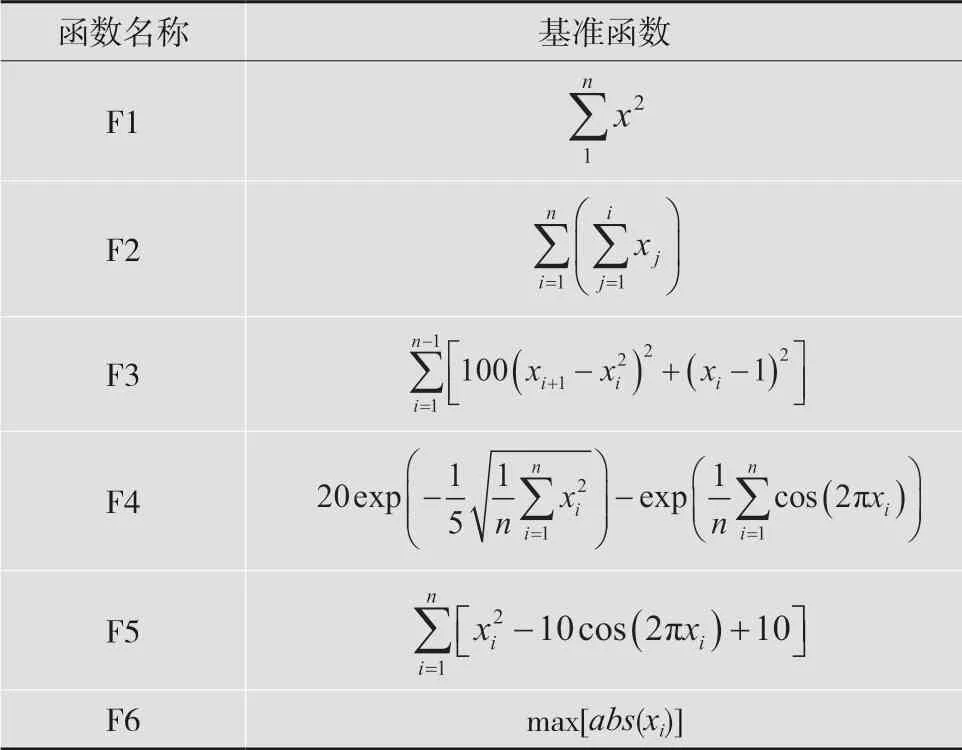
表1 基准函数

表2显示了两种算法在6个基准函数的不同维度下的最优值和方差对比，从表中的数据可以发现WOA-SOS相比于WOA算法具有更好的性能，这也说明其在种群初始化、自适应因子和个体筛选方面能够显著地提高算法的性能，尤其在维度较高的方面表现更加明显。

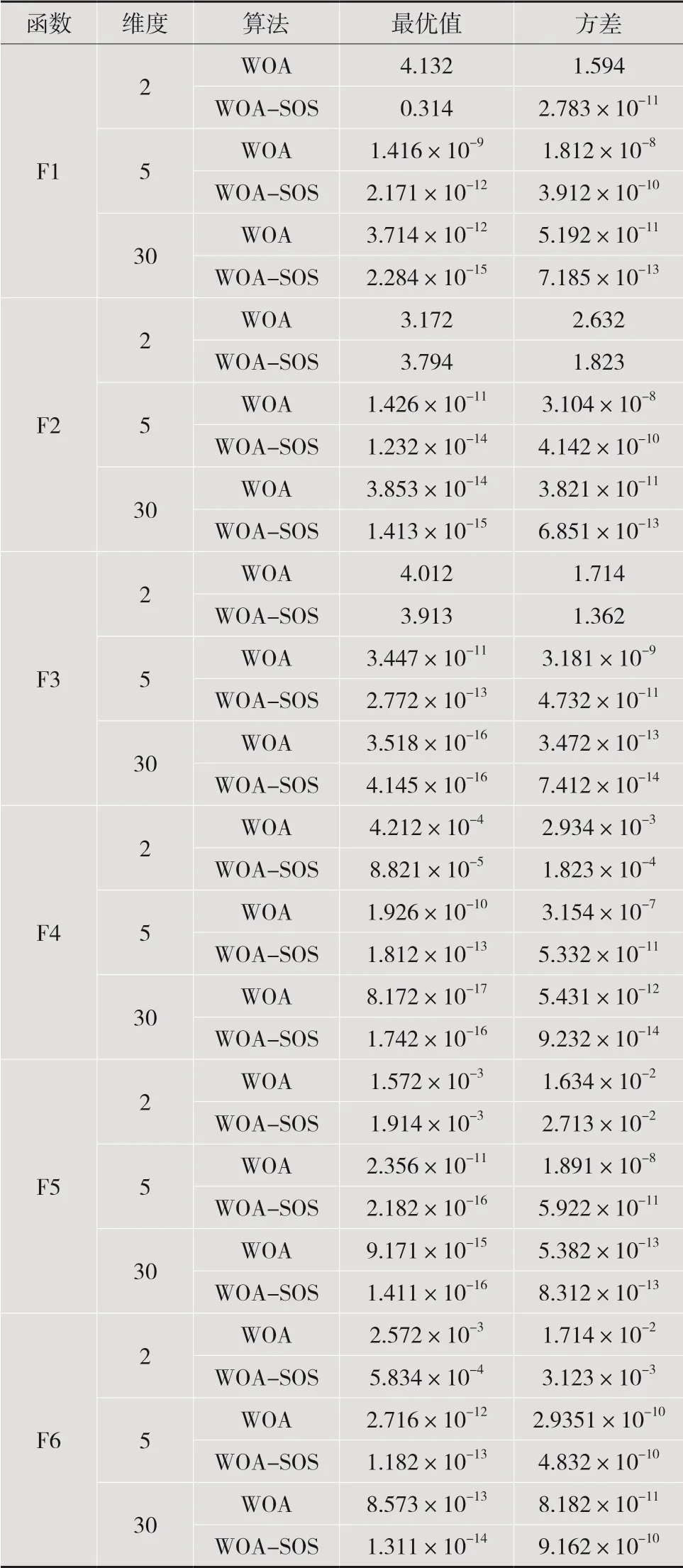
表2 两种算法在不同基准函数的优化结果

4.2 节点定位指标对比

为了说明WOA-SOS算法在节点定位中的效果，本文从节点密度、锚节点比例、通信半径及区域面积4个指标方面与WOA算法进行比较。本文选择100个传感器节点随机分布于10 m×10 m的二维区域中，锚节点个数占据20%，通信半径设置为1～3 m。

图1显示了两种算法在不同的节点密度下的节点定位带来的误差效果的对比。从图1可以发现，随着节点密度的不断增加，使用两种算法产生的节点定位曲线都呈现误差逐渐减小的趋势。从效果上看，使用本文算法产生的定位误差影响更小，说明WOA-SOS算法的性能得到了提升，因此在定位误差方面具有一定的优势。

图1 不同节点密度的定位误差对比

图2显示了两种算法在锚节点数量不同的情况下的节点定位对比。从图2可以发现，随着锚节点数量的增加，定位误差会逐渐减少，但是由于WOA-SOS算法具有良好的性能，定位效果明显优于WOA算法，这也说明了使用WOA-SOS算法在节点定位中能够有效地减少误差。

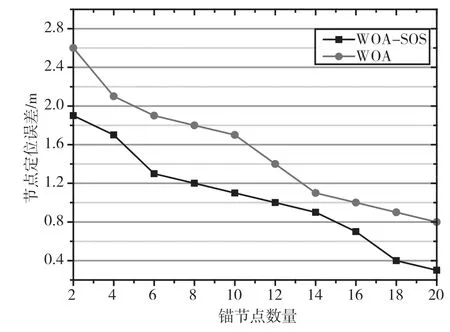
图2 不同锚节点数量下的定位误差对比

图3显示了不同的通信半径下两种算法的定位误差对比效果。从图3可以发现，随着节点通信半径逐渐增大，锚节点数量逐渐增大，定位效果具有明显的提升。但是WOA-SOS算法性能的提升在一定程度上提高了节点定位的精度，从图3的效果来看，WOA-SOS算法性能明显优于WOA.

图3 不同通信半径下的定位误差对比

图4显示了两种算法在不同区域面积下的定位误差对比效果。从效果来看，随着区域面积逐渐增大，两种算法的定位误差都有不同程度的上升，这说明节点定位和区域面积具有一定的关系。尽管WOA-SOS算法性能具有较大的优势，但是也不能弥补区域面积增大带来的影响。但是从整体上看，WOA-SOS算法具有明显的优势。

图4 不同区域面积下的定位误差对比

5 结 语

针对无线传感网络中节点定位存在误差大、精度低的问题，本文提出了基于WOA-SOS的节点定位算法。该算法通过种群的初始化、自适应因子调节和个体筛选提高了算法性能，在节点定位中的节点密度、锚节点比例、通信半径及区域面积四个指标中具有较好的定位效果，有效地降低了定位误差。