基于熵产理论的竖井贯流泵流动损失特性

张 睿，谭舒翊，丁旭洁，徐 辉，冯建刚，牟 童，费照丹

(1.河海大学农业科学与工程学院，江苏 南京 211100； 2.河海大学水利水电学院，江苏 南京 210098)

竖井贯流泵属于低扬程、大流量的高比转速泵，具有进出水流道顺直、水力损失相对较小、机组结构简单紧凑、便于管理和维护等优点，因此被广泛应用于农业灌溉、防洪排涝以及区域调水等领域，例如江苏的梅梁湖泵站、江尖泵站、运河东枢纽泵站、邳州泵站等工程均采用了竖井贯流泵[1-2]。竖井贯流泵通常在设计流量工况附近运行时内部流态好、工作效率高、机组运行稳定，但是进入小流量工况范围运行时，竖井贯流泵容易进入马鞍区[3-5]，此时泵内流动变得十分紊乱，叶轮容易发生旋转失速，进而严重影响水泵机组的安全稳定高效运行。

目前，国内外很多学者围绕混流泵、轴流泵马鞍区工况下的水力特性及内部非稳定流动特性等方面开展了试验和数值模拟研究。Miyabe等[6]利用DPIV技术并结合压力脉动测量研究了混流泵马鞍区工况下叶轮出口与导叶进口之间的大尺度回流及旋涡流动现象，并阐明了马鞍区形成的机理。Goltz等[7]采用高速摄影和油流技术对马鞍区工况下的轴流泵内部流场进行了观测，在深度失速工况时捕捉到叶轮通道内会产生垂直叶片表面的通道涡结构。施卫东等[8]采用PIV技术研究斜流泵内部流动特性，分析了不同相位下叶轮内部流动特性及涡量分布，得到小流量工况下叶轮的涡量变化。程千等[9]基于SSTk-ω模型对马鞍区工况下的轴流泵内部流场进行了数值模拟，发现进水流道内的螺旋形回流在剪切作用下会与主流相互作用形成回流涡。王勇等[10]采用RNGk-ε模型对轴流泵马鞍区工况流场进行了研究，结果表明马鞍区工况下叶片吸力面出现较大的低压区和漩涡集中区。李恩达等[11]基于RNGk-ε模型对混流式喷水推进泵马鞍区工况的流场进行了数值计算，并从内流特性、流动参数等角度对马鞍区工况对应的状态进行了系统分析。

马鞍区工况下泵内流动十分紊乱，势必会引起较大的能量损失。而熵产能够有效反映流动损失的大小，因此越来越多的研究者采用熵产理论开展水力机械内部流动损失特性方面的研究[12-15]。Hou等[16]和Li等[17]采用局部熵产法分别对离心泵和混流泵的能量损失进行了研究，验证了熵产理论的可行性。张永学等[18]应用熵产理论对离心泵耗能进行了评价，得出叶轮和蜗壳是熵产的主要区域，且主要类型为壁面熵产和湍流熵产。冯建军等[19]应用熵产理论研究了离心泵断电过渡过程，获得了各部件的能量损失情况。Chang等[20]通过熵产理论分析了叶片厚度对水力损失的影响。Yang等[21]利用熵产理论系统分析了离心泵诱导轮与叶轮间的时序效应对性能的影响。

目前，有关竖井贯流泵马鞍区工况下内部流动特性的研究相对较少，尤其是对于各过流部件的流动损失特性有待进行定量分析。本文以某新建泵站选用的竖井贯流泵为研究对象，采用CFD方法对其内部流场进行数值计算，分析各典型流量工况特别是马鞍区工况下泵内流动特性，并基于熵产理论分析各部件的能量损失分布规律，以期为竖井贯流泵的水力优化设计提供参考。

1 数值模拟方法

1.1 几何模型与网格划分

本文研究的竖井贯流泵为前置式竖井贯流泵，其三维几何模型如图1所示。其中，数值计算的区域主要包括进水流道、叶轮段、导叶体和出水流道等4个部分。竖井贯流泵的主要几何及性能参数如下：设计流量QB=0.338 m3/s，设计扬程HB=4.78 m，叶轮直径D=0.3 m，叶顶间隙δ=0.25 mm，转速n=1 248 r/min，叶轮叶片数Z1=4，导叶叶片数Z2=6。

图1 竖井贯流泵三维模型

采用ANSYS ICEM CFD软件对竖井贯流泵计算区域进行网格划分(图2)，其中进水流道因其结构复杂，故采用自适应性较强的非结构化网格，其他部分为保证计算网格具有较好的正交性及较高的质量而采用结构化网格。叶轮叶片采用J型拓扑，导叶叶片采用H型拓扑，叶轮和导叶近壁面采用O型拓扑并进行加密处理。

图2 竖井贯流泵网格划分

采用基于Richardson外推法的GCI方法[22]对计算网格误差进行预估。网格尺度h为

(1)

式中：ΔVi为第i个网格单元的体积；N为网格的单元总数。

根据整体计算域确定流场的平均h值，分别设置N1、N2、N3不同数量的网格，得到相应的网格尺度h1、h2、h3，网格细化比例r21=h2/h1，r32=h3/h2，一般取大于1.3的值。采用定点迭代法求解网格收敛精度等级系数pr与迭代参数q：

(2)

(3)

其中ε32=φ3-φ2ε21=φ2-φ1

式中φi为第i个网格误差的评定变量。

计算收敛后，φ的外推值φe为

(4)

分别计算近似相对误差估计值ea、外推值相对误差ee、精细网格收敛指数If：

(5)

(6)

(7)

以设计工况为例，分别设置N1=825 474、N2=2 009 275、N3=4 913 279的3组不同网格数量方案，网格细化比例r21=1.347，r32=1.345。评价指标参数选择扬程系数H*、功率系数P*和效率系数η*等3个无量纲数[23]：

(8)

(9)

(10)

式中：Qv为质量流量，kg/s；p2为出口总压，Pa；p1为进口总压，Pa；T为转矩，N·m；ρ为水的密度，m3/s。

计算结果表明，扬程系数、功率系数和效率系数的If均在5%以内，表明N3的网格离散误差较小，具有良好的计算精度，此时叶轮区域的网格数为2 007 392，导叶体的网格数为1 005 840。

1.2 计算方法与边界条件设置

考虑到旋转曲率修正的滤波器湍流模型(FBM-CC)可以较好地捕捉湍流多尺度信息且增强了对流动曲率效应的敏感性，有助于提高水力机械的数值计算精度[24]，因此本文基于非定常雷诺时均法(URANS)、采用FBM-CC湍流模型开展竖井贯流泵内部流场的非定常计算。

流体介质为25℃时的水，进口边界条件为流量进口，出口为自由出流，边壁为无滑移壁面，收敛精度为10-5。定义叶轮为旋转域，动静交界面设置为瞬态转子定子类型。

在进行非定常计算时，以定常计算结果为初始条件，时间步长设置为2×10-4s，即叶轮旋转1.5°，总时间为15个叶轮旋转周期，并选择最后5个旋转周期的结果进行统计分析[24]。

2 熵产理论

为了系统分析竖井贯流泵内流动损失分布，引入熵产理论。熵产是由于过程中存在不可逆因素引起的耗散效应，使系统损失的机械能转化为内能。在水泵系统内，流动分离、漩涡等不良流态会引起熵产增加，动能、压能等转化为内能也会引起熵产增加[19]。在此次计算中由于水的比热容比较大，认为温度不变，不考虑传热引起的熵产。

对于湍流运动，熵产主要包含2部分，即由时均速度引起的直接耗散熵产S1和脉动速度引起的湍流耗散熵产S2[25]；同时，由于存在壁面效应，需要计算壁面摩擦损失产生的壁面熵产S3[26-27]，因此总熵产S为

S=S1+S2+S3

(11)

(12)

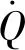
(13)

(14)

式中V为计算域体积，m3。

(15)

式中ε为湍动能耗散率，m2/s3。

(16)

(17)

式中：τ为壁面剪切应力，Pa；v为壁面区第一层网格中心的相对速度矢量，m/s。

(18)

式中A为计算域表面积，m2。

将式(14)(16)(18)代入式(11)即可求得总熵产。

3 计算结果与分析

3.1 水力性能分析

图3为竖井贯流泵的水力性能数值模拟和模型试验结果对比，可见数值模拟预测的竖井贯流泵各工况点的水力性能与试验测量的结果吻合程度较好，表明本文采用的数值模拟计算方法对竖井贯流泵水力性能预测具有良好的可靠性。另外，由图3可知，随着竖井贯流泵的流量降低至0.62QB(临界失速工况)，扬程开始出现下降趋势，Q～H曲线呈现明显的正斜率，当流量降低至0.58QB(深度失速工况)以下时，Q～H曲线又恢复为负斜率变化。

图3 数值模拟与模型试验水力性能对比

表1 不同区域的熵产分布特征

表2 叶轮段的熵产分布特征

3.2 流动损失特性分析

为研究竖井贯流泵典型流量工况下的流动损失特性，基于时均统计结果，选择0.54QB、0.56QB、0.58QB、0.62QB、0.70QB和QB工况进行对比分析。表1为不同区域的熵产分布特征，其中，熵产比率是指某部分熵产值占总熵产值的比例。可以看出，总熵产值和各区域的熵产值均随流量的减小而增大，QB工况下熵产值最小(5.83 W/K)，0.54QB工况下熵产值最大(14.14 W/K)，两者相差约为1.4倍。熵产值出现较大变化的流量区域为0.56QB～0.70QB(总熵产值)、0.58QB～0.62QB(叶轮段)和0.56QB～0.58QB(进水流道)，在此范围内熵产值分别相差6.21 W/K、1.37 W/K和0.94 W/K，说明存在较大的能量波动。各区域能量损失从大到小依次为叶轮段、出水流道、导叶体、进水流道。还可以看出，叶轮段熵产比率最大，在QB工况下可达到49%；进水流道熵产比率最小，在0.62QB工况下为4%。说明叶轮段是泵内能量损失的主要区域，因此需要对叶轮段内部进行重点分析。

表2为叶轮段3种不同类型的熵产分布特征，可以看出直接耗散熵产几乎可以忽略，湍流耗散熵产随流量增大逐渐减小，壁面熵产随流量增加呈现先减小后增大的趋势，0.62QB工况下壁面熵产最小，为0.21 W/K。根据式(17)，壁面熵产与壁面剪切力和速度有关，小流量工况下剪切力是主要影响因素，随着流量增大剪切力降低引起壁面熵产降低；流量增大到一定程度后，流速逐渐成为主导因素，所以壁面熵产又会增加。从表2还可以看出，湍流耗散熵产最大，壁面熵产次之，直接耗散熵产最小。0.54QB～0.62QB工况下湍流耗散熵产的熵产比率均在80%以上，0.70QB工况可达92%，说明竖井贯流泵马鞍区工况下叶轮段能量损失的主要来源是湍流耗散。

3.3 叶轮内部流动特性分析

图4 不同流量工况的局部熵产率

图5为4种典型流量工况下10%和90%叶高截面上的相对速度流线。QB工况时，流线整体均匀分布，未出现流动分离；0.62QB工况时，10%叶高截面出现明显的流动分离且在叶片吸力面尾缘出现大尺度漩涡，叶片尾部流线几乎垂直流向相邻叶片压力面，反映出叶轮通道部分区域被通道涡堵塞，同时叶片压力面侧也出现了分离涡，而90%叶高截面上流动相对比较稳定；0.58QB工况与0.62QB工况相比，10%叶高截面上吸力面尾缘漩涡范围有所减小，但90%叶高截面上流线几乎垂直流向与叶片压力面前缘，结合表1，叶轮段的熵产值在0.58QB工况出现大幅上升的原因是叶片轮缘处产生了不良流态；0.54QB工况与0.58QB工况相比，10%叶高截面上漩涡范围扩大，叶轮通道依然堵塞严重，90%叶高截面上叶片吸力面前缘出现明显分离涡。对比图4和图5，可以发现叶轮的局部高熵产区域与不良流态相对应，这也证明了熵产理论的可靠性。

图5 不同流量工况的速度流线

为进一步揭示泵内部流态，定义一个无量纲变量W：

(19)

截取叶轮的部分轴截面，绘制不同流量工况叶轮区域的W值分布及速度流线图如图6所示(图中SS为叶片吸力面，PS为叶片压力面)。可以看出，QB工况叶轮内部流线分布均匀，轮毂靠近叶轮出口处W接近1，说明此处具有较好的轴向入流状态；0.62QB工况轮毂靠近叶轮出口处出现较大的负W值区域，对应流线在此处出现回流，同时，与QB工况相比，W接近1的区域向轮缘方向偏移，结合图5(b)，轮毂处存在漩涡；0.58QB工况轮毂处回流范围明显扩大，同时，叶轮进口轮缘处有负W值区域，出现了与主流方向相反的叶顶间隙泄漏流，结合图5(f)，叶顶间隙泄漏流对主流造成干扰，影响叶片前缘进流，导致轮缘处进流流态恶化；0.54QB工况叶轮进口轮缘处的负W值区域向进口方向延伸，进水流道内出现大范围回流，结合表1中0.54QB工况进水流道较大熵产，说明流量减小到0.54QB工况后，叶顶间隙泄漏流对主流造成干扰，影响叶片前缘进流，导致流态恶化，还导致较大能量损失。

图6 不同流量工况叶轮区域轴截面的W值分布及速度流线

4 结 论

a.竖井贯流泵在不同流量工况下采用FBM-CC模型的数值模拟结果与试验结果的误差在5%以内，表明FBM-CC模型可以有效预测竖井贯流泵水力性能。

b.竖井贯流泵各工况下能量损失从大到小依次为叶轮段、出水流道、导叶体、进水流道，其中在设计工况时，叶轮段熵产比率最高，达到49%；叶轮段各工况下湍流耗散熵产最大，壁面熵产次之，直接耗散熵产最小，其中临界失速工况下熵产比率分别为92%、6%和2%，说明湍流耗散是能量损失的主要因素；直接耗散熵产几乎可以忽略，湍流耗散熵产随流量增大逐渐减小，壁面熵产呈现先减小后增大的规律。

c.马鞍区工况范围，叶轮区域内部的漩涡流动和流动分离引起局部高熵产。临界失速工况下轮毂处叶片吸力面尾缘出现大范围漩涡，叶轮通道被通道涡堵塞，压力面出现分离涡，这些区域存在较大能量损失，轮缘处流动相对较稳定；深度失速工况下叶顶间隙泄漏流对主流造成干扰，叶轮进口轮缘处出现流动分离，流量继续减小时进水流道内流态受到影响，叶片前缘出现分离涡。