基于Shi-Tomasi角点验证的线段提取算法优化方法

骆开庆， 邓军灿， 蔡伟博， 周育滨， 张 健

(华南师范大学物理与电信工程学院/电子与信息工程学院/广东省光电检测仪器工程技术研究中心， 广州 510006)

直线段是数字图像中常见而重要的几何元素，在图像中表现为一组不间断的像素集合，集合内的像素一般具有近似的灰度值和梯度方向。目前主流的线段检测方法是感知分组算法，这类算法一般先从图像中提取边缘或梯度信息等特征，再利用像素集合内各个像素的相邻性和连续性将共线特征扩展为直线段区域。

1992年，ETEMADI[1]提出了基于图像边缘的线段提取方法。随后，TOPAL和AKINLAR[2-3]提出了一种高效的边缘绘制算法，并在此基础上提出了一款快速的直线段检测算法(EDLines，Edge Drawing Lines)。基于边缘的方法依赖边缘提取算法的准确性，但边缘提取的过程中会丢失部分有用信息。为此，BURNS等[4]提出了一个直接基于图像梯度的直线段检测思路，但由于忽略了梯度幅度值，检测效果不够理想；GROMPONE等[5]提出了一个快速的检测直线段方法(LSD，Line Segment Detector)，通过设定像素梯度幅值的最小值来抑制错误线段的产生，并且根据文献[6]提出的错误报警数(NFA，Number of False Alarm)，对初步提取的直线段区域进行验证；HAMID和KHAN[7]提出了一种基于角度和空间接近度的方法(LSM，Line Segment Merging)，但该方法将紧密平行的多条线段合并为一个线段，并且缺乏验证步骤，其结果不可靠；SUREZ等[8]提出了一种基于快速线段分组的直线检测方法(FSG，Fast Segment Grouping method)，该方法利用贪婪算法对线段进行分组，并且用概率模型决定一组线段是否合成为一条线段，但是该合成线段的长度与真实线段会有较大偏差；SALAUN等[9]提出了多尺度线段检测方法(MLSD，Multiscale Line Segment Detector)，判定合并线段的NFA应该大于任何一条被合并的线段，但是NFA中直线段区域的宽度需要人为设定。感知分组算法能在特征模糊区域提取到线段，而在该区域提取到的线段往往为无意义线段。因此，学者们提出了多种解决办法。如：CHO等[10]提出了一种新的基于线段的表示方法(Linelet)来模拟栅格化图像空间中线段的内在属性，并构建了线段检测框架、线段验证框架和线段合并框架；LIU等[11]和LI等[12]在LSD的基础上进行了适配性改进，分别提出了LSDSAR和ULSD，使其能够在一些特殊图像上进行线段提取，如产生畸变的图像或SAR图像，提高了算法的适用范围；XUE等[13-14]提出了一种基于区域划分的线段地图吸引场对偶表示方法，将线段检测问题作为区域着色问题，然后通过深度学习卷积神经网络来提高准确性、鲁棒性和效率,并在不丢失信息的情况下将吸引场重新映射为一组线段。目前，线段提取算法虽已有许多改进，但其无意义线段多的问题仍得不到很好的解决。

角点作为空间上另一个重要的几何元素，在保留图像特征的基础上有效地减少了信息量，提高了图像处理速度和实验精度。由于角点周围梯度值的变化速率高，大部分线段的周围会存在角点，特别是端点和线段连接处。目前主流的角点检测算法是基于灰度变化的角点检测算法，如：MORAVEC[15]通过计算灰度变化，选取最小的灰度方差作为角点响应值进行非极大值抑制确定角点；HARRIS和STEPHENS[16]在Moravec算法的基础上提出通过微分运算和自相关函数来提取角点，并称该方法为Harris角点检测算法；SHI和TOMASI[17]改进了Harris算法的角点响应函数, 提出了Shi-Tomasi算法，使提取的特征点分布更均匀合理，角点提取效果显著提升；SMITH和BRADY[18]提出了SUSAN算法，通过计算规定区域内的相似像素的数目来验证角点；ROSTEN等[19-20]提出了经典的FAST与FAST-ER图像角点检测算法，通过统计在中心像素附近梯度大于中心像素梯度的像素数目来验证中心点是否为真实角点。

基于上述分析，本文提出了一种基于Shi-Tomasi角点验证的线段提取算法优化方法(ST-Lines算法)。该算法在经典的线段提取方法中加入Shi-Tomasi角点，利用获得的角点及其分布特性，对线段进行验证，以实现无意义线段的精准剔除。并在YorkUrban线段数据集上，将ST-Lines算法与原始LSD线段提取算法[6]、原始EDLines线段提取算法[3]、Linelet算法[10]、LSM算法[7]进行对比实验。

1 线段提取优化算法

1.1 Shi-Tomasi角点检测

角点在任意一个方向上做微小移动，都会引起该区域的梯度图的方向和幅值发生很大变化。基于这一特性，本文将角点应用于优化线段提取算法。

Shi-Tomasi算法[17]设定了一个固定尺寸的窗口(小的图像片段)W(x,y)，其像素灰度值为I(x,y)，将该窗口向x、y方向分别移动微小位移u、v，移动后的新位置对应的像素灰度值为I(x+u,y+v)，则可得该窗口此次移动引起的灰度值的变化值[I(x+u,y+v)-I(x,y)]。同时，设高斯核函数ω(x,y)为W(x,y)的窗口函数，表示窗口内各像素的权重。如果窗口中心像素点是角点，则其灰度值变化剧烈，该点的权重系数较大，表示该点对灰度变化的贡献较大；而离窗口中心(角点)较远的点，其灰度值变化较小，该点的权重系数也较小。如图1，该窗口向各个方向移动(u,v)，其产生的灰度值变化量E(u,v)可以表示为：

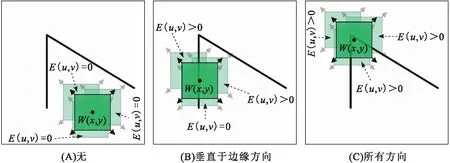
图1 Shi-Tomasi算法中窗口滑动时灰度值变化较大的方向

(1)

对于1个角点来说，为了简化式(1)的运算，对I(x+u,y+v)用泰勒公式展开：

I(x+u,y+v)≈I(x,y)+uIx+vIy，

(2)

其中，Ix、Iy分别表示图像灰度在x、y方向上的梯度值。进而将式(1)推导为：

(3)

(4)

由式(3)可知，灰度值的变化大小取决于矩阵M，为了找到引起较大灰度值变化的窗口，可以利用矩阵M的特征值λ1、λ2来计算每个窗口对应的角点响应函数R。设定一个阈值τc，若像素点对应的R满足如下条件：

R=min(λ1,λ2)>τc，

(5)

则该点被设定为角点。

1.2 角点非极大值抑制

角点提取容易受到图片环境的影响，如在某些物体上会产生大量角点，极大地增加后期处理的计算量。为了提高角点的质量以及运算的速度，本研究对拥有过于密集角点的区域进行角点非极大值抑制。具体步骤(图2)如下：

图2 通过滑动窗口对角点进行非极大值抑制

(1)角点检测：对数据集的图片(640 px×480 px)使用Shi-Tomasi角点检测算法。在Shi-Tomasi角点检测算法中，角点最小间隔设定为3 px；质量因子设定为0.05，表示可接受角点的最低质量水平为0.05；算法内的其他参数均为默认值。

(2)滑动窗口：设置了一个40 px×40 px的窗口，在该图片上按从左到右、从上到下的运动规则滑动，滑动步长设定为20 px。

(3)角点抑制：如果窗口内角点个数大于30个，则将角点算法的角点最小间隔调整为6 px。此时，窗口内能够提取到的角点个数为(40/6-1)2≈30个。对该窗口重新提取角点，进行角点非极大值抑制，使得区域内最大角点数只能是30个。

(4)最终角点：得到角点非极大值抑制后的最终角点。

1.3 有无意义线段验证

图像中角点周围的梯度值变化剧烈，这意味着大部分线段的周围会存在角点，特别是端点和线段连接处。而一些无意义线段由于其特征比较模糊，梯度变化速率比较小，周围往往没有分布角点。感知分组线段提取算法能在特征模糊区域提取到线段，是因为此类区域梯度幅值较大时，算法梯度阈值如果设置不当则无法屏蔽此类区域的像素，进而提取出无意义线段。另外，不同环境的最佳梯度阈值是不相同的，而更改梯度阈值不切实际。在云、玻璃和地板等特征模糊区域往往会出现无意义线段，而其周围的角点数目很少或为零(图3)。已有的角点检测算法结果[15-20]表明，角点较少分布在特征模糊区域的现象具有一般性。因此，利用角点分布的特性，可剔除掉一些周围没有角点的无意义线段，保留特征更加明显的有意义线段。

图3 部分特征模糊区域的线段和角点分布

本文算法在进行角点检测和线段检测后，将线段从长到短排序，按图4中的3个步骤遍历每一条线段si并进行验证。若线段满足其中一个步骤的条件，则将其放入有意义线段MS(Meaningful Segment)集合；若都不满足，则为无意义线段。最终，MS集合收集了所有的有意义线段。

图4 线段验证总流程图

具体的线段验证步骤(图4)如下：

步骤(1)：长线段验证。一般来说，线段越长，线段所在区域的特征越明显，则线段越有意义。当被检测的线段大于mean(S)的2倍时，直接认定为有意义线段，予以保留，即满足以下条件：

(6)

其中，N为线段总数量，mean(S)为全部线段的平均值。此条件可以将长线段直接认定为有意义的线段，从而加快处理速度。

步骤(2)：线段端点圆形框内角点统计验证。对于不满足步骤(1)条件的剩余线段si，以线段端点为中心，设定1个半径为τd的圆形框进行角点统计。考虑到Shi-Tomasi算法所采用的角点最小间隔为3 px，为了保证圆形框能把线段端点周围的角点选中，本文设置τd=3 px。线段端点圆形框内角点统计方法如图5所示。

图5 线段端点圆形框内角点统计方法

在图5中，圆形框内角点集合CCi存放着离si端点较近的角点。若角点cm满足以下条件，则认为该角点是CCi的元素：

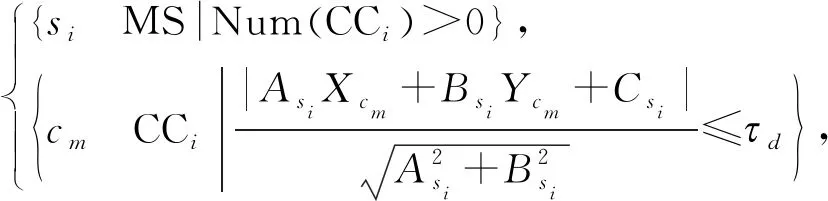
(7)

其中，Asi、Bsi和Csi为线段的参数；Xcm和Ycm为角点cm的坐标。当CCi的元素个数大于0时，即被检测线段周围存在角点，则认定该线段有意义，予以保留。

步骤(3)：KNN算法验证。不满足上述步骤条件的剩余线段仍然可能存在有意义线段。由于特征明显的区域内有意义线段的聚集性，本步骤将对周围没有角点但长度大于平均长度的线段，使用KNN算法进行再次验证。KNN算法验证方法如图6所示，可具体表述为：以被检测线段si的中心为圆心、该线段的一半长度为半径画圆，sy为与该圆有交集的线段，计算圆内有意义线段总长度 lenmf以及无意义线段总长度 lenml。若si满足以下条件：

图6 KNN算法验证方法

(8)

即 lenmf>lenml，则认定si是有意义线段，予以保留。否则将其剔除。

水资源是区域经济社会发展的基础性资源之一，也是区域生态与环境的控制性要素。宁夏地处西北内陆干旱地区，水资源极为匮乏，属于重度缺水区。对于宁夏严峻的水资源形势，开展建设项目水资源论证工作，有利于保护建设项目的合理用水，提高用水效率和效益，使有限的水资源在宁夏经济社会发展中发挥更大的作用。

通过以上3个步骤的验证，大部分在特征模糊区域的无意义线段被检测并剔除，而在特征明显区域的有意义线段则尽可能保留，处理效果如图7。

图7 无意义线段剔除效果

2 实验结果与分析

为了验证基于Shi-Tomasi角点验证的线段提取算法优化方法，比较线段提取算法EDLines、LSD、LSM、Linelet和基于Shi-Tomasi角点验证优化后的EDLines、LSD在数据集上的平均准确率、平均召回率、F-score、平均线段数量、平均线段长度以及运行帧率。

2.1 实验准备

2.1.1 数据集 选用YorkUrban线段数据集[21]来进行线段提取算法测试，该数据集由45幅室内图像和57幅室外图像组成，图像分辨率为640 px×480 px。

2.1.2 实验环境 为了保证公平性，在线获取被比较方法的源代码，并使用默认参数执行。除了在MATLAB中运行的LSM和Linelet外，所有的方法都是用C++编程语言实现的。评估代码采用CHO[10]提供的开源代码，实验平台为：操作系统为Ubuntu 18.04，64位的台式电脑，Intel Core i5 8300 CPU@ 2.30 GHz 8 GB内存，运行环境为CLion 2.0。

2.1.3 评估指标 为了合理、全面地评价该方法的性能，采用的指标有：平均准确率(AP)、平均召回率(AR)、F-score、平均线段数量(NUM)、平均线段长度(LENGTH)、运行帧率(FPS)。根据正确检测到的线段数量(即真阳性的数量(TP))、错误检测到的线段数量 (即假阳性的数量(FP))和存在于图像中但未被算法检测到的线段数量(即假阴性的数量(FN))，精度、召回率和F-score可定义为：

(9)

对于每一条来自真实数据集的线段sgt，在所检测到的线段中寻找满足以下条件的集合{sp}:

(10)

da(θgt,θp)≤λang，

(11)

其中，λdist、λang分别为距离阈值、角度阈值，θgt、θp分别为sgt、sp的角度，dp(sgt,sp∣θgt)为sgt与sp的中心在θgt上的垂直距离，da(θgt,θp)为两者之间的角度差。

若{sp}和sgt的重叠占比大于重叠占比阈值λarea：

(12)

则认为{sp}与sgt特征相符。设λdist=1,λang=5°,λarea=0.75。为了检验算法提取准确线段的能力，本文设置了严格的参数，这使得各类方法的平均准确率都比较低。

2.2 结果分析

2.2.1 数据集结果对比实验 由表1可知：ST-Lines算法(EDLines+Corner、LSD+Corner)在平均准确率、F-score、线段平均数量、线段平均长度上比原线段提取算法(EDLines、LSD)、LSM算法、Linelet算法有更好的表现。究其原因为：角点验证方法可以将无意义的、在真实数据里不出现的线段剔除掉，从而提高了平均准确率、F-score，降低了线段平均数量；由于所剔除的线段往往是破碎的短线段，所以提高了线段的平均长度。然而，ST-Lines算法无法完全保留有意义线段，并且它是在原线段提取算法上做改进，所以该算法在召回率和运行帧率上轻微低于原线段提取算法。由图8A可知：对于数据集的每张图片，ST-Lines算法所提取的线段在平均准确率上普遍高于其他算法，证明了 ST-Lines算法能在各种场景下剔除特征模糊区域中的无意义线段。由图8B和图8C可知：在大部分场景下，ST-Lines算法的平均准确率高于原线段提取算法的，证明了该算法的有效性。

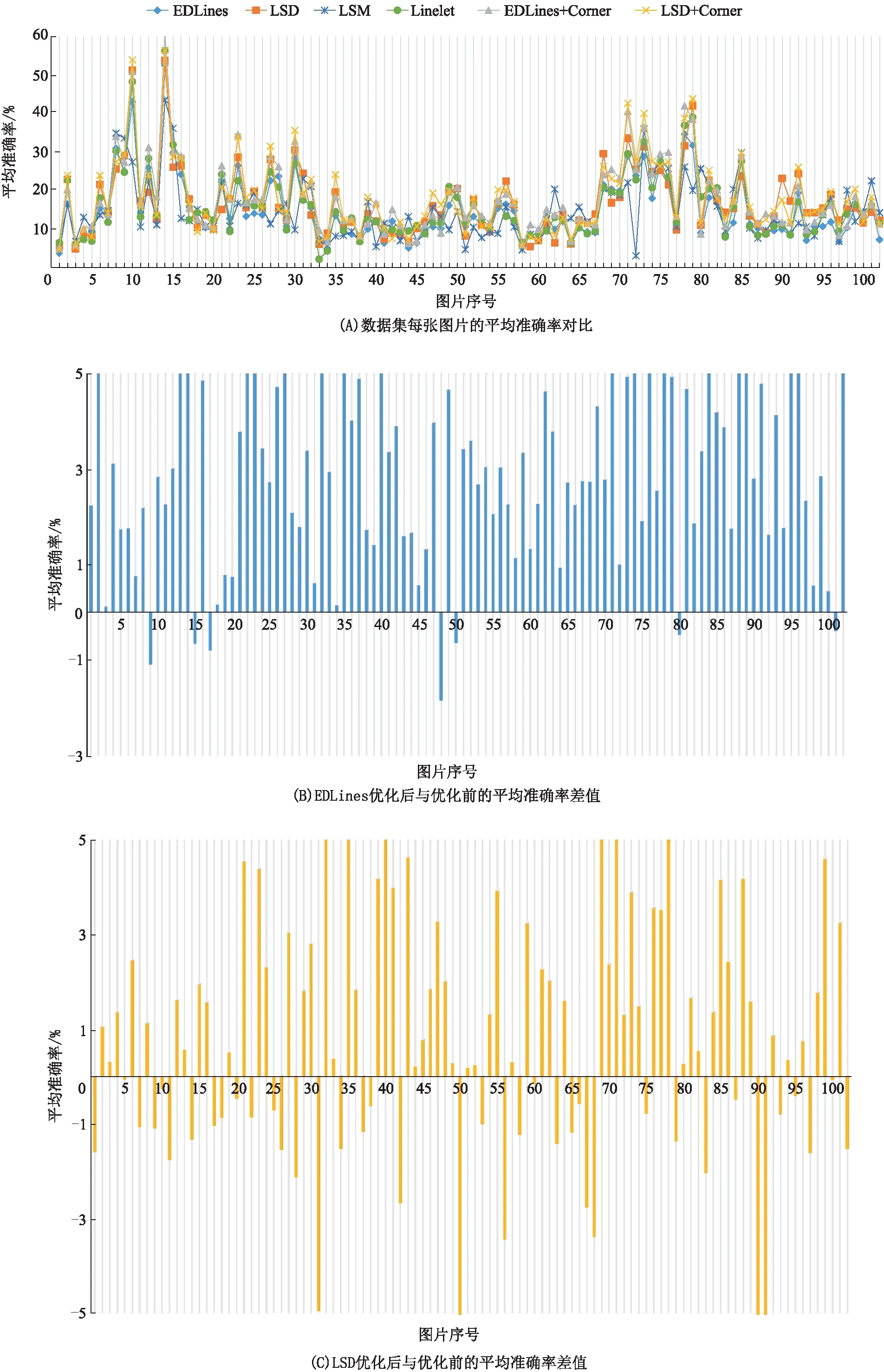
图8 数据集中每张图片的结果对比

表1 6种算法在数据集的平均结果对比

2.2.2 室内外场景结果对比实验 为了直观地展示角点验证优化的效果，分别提取了3张室外场景和室内场景的图片，将原图、真实线段数据、原线段提取算法(EDLines、LSD)、ST-Lines算法(EDLines+Corner、LSD+Corner)的结果进行比较。

由图9A可以看出，原线段提取算法(EDLines、LSD)从天空的云朵中提取出无意义线段，此类线段的鲁棒性较低，对后续工作(如三维重建、线段匹配等)没有意义。此外，在室内外交接的地方，由于光线射入地板，引起地板上一些不明显的条纹的梯度增强，造成线段误提取。由图9B可以看出，室内场景的灯光经常照射在墙壁、天花板和地板等位置，造成局部区域梯度增强，而往往灯光的光强分布不均匀，造成原线段提取算法(EDLines、LSD)在此类特征模糊区域误提取的线段短小且杂乱，无统一方向。综上可知：无论是室内场景还是室外场景，ST-Lines算法(EDLines+Corner、LSD+Corner)算法可以很好地剔除无意义线段，保留有意义线段，证明了该算法的可靠性。

图9 4种算法的室内外场景结果

2.2.3 不同评估标准下的算法性能对比实验 参数重叠比阈值λarea是评估标准中最重要的参数，该参数的意义是：一条检测线段如果被评估为检测正确的，那么该检测线段与其所对应的真实线段的重叠比要大于λarea。为了展示ST-Lines算法在各个评估标准下的性能，在不同的λarea下对ST-Lines算法进行测试。

由测试结果(图10)可知：对于任意λarea(λarea[0.05,0.95])，ST-Lines算法(EDLines+Corner、LSD+Corner)的F-score高于原线段提取算法(EDLines、LSD)的，说明角点验证优化后的算法效果不是在某一评估标准具有优势，而是在全部评估标准中都具有优势，体现了角点验证算法的效果具有代表性。

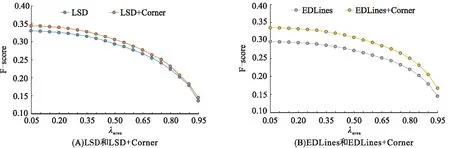
图10 不同λarea 下4种算法的F-score的变化曲线

3 结论

本文提出了一种基于Shi-Tomasi角点验证的线段提取算法优化方法(ST-Lines算法)。该算法在对图像进行经典线段提取后，首先采用Shi-Tomasi角点检测提取角点，然后利用滑动窗口对所得的角点进行非极大值抑制，再根据线段长度、线段圆形框内的角点分布和KNN算法验证每条线段，从而剔除无意义线段。最后，利用YorkUrban线段数据集，对ST-Lines算法与原线段提取算法以及其他先进算法(Linelet、LSM)进行测试对比。实验结果表明：ST-Lines算法在平均准确率、F-score和平均线段长度上有所提高，且降低了平均线段数量。该方法可进一步应用于更复杂的算法中，如：三维重建算法、线段匹配算法、SLAM算法等中的线段提取优化。