N2和O2在δ-Pu(100)表面吸附行为的理论研究

赵朝阳， 王国亮， 翟鹏飞， 戚春保， 陈旭丹

(火箭军工程大学核工程学院， 西安 710025)

金属钚(Pu)在国防、航天和能源领域具有重要的作用，它位于包含离域5f电子的轻锕系元素和包含局域5f电子的重锕系元素之间，电子性质极为复杂，具有奇异的f-f电子相互作用和明显的相对论作用[1]。钚的化学性质非常活泼，易与空气中的H2、O2、H2O、CO2、N2和CO等多种活性气体发生相互作用，导致表面发生腐蚀，给钚材料的储存和使用带来不利影响。早期的实验研究[2-3]表明，钚的氧化腐蚀速率和空气湿度有关，在室温下，潮湿空气中钚的腐蚀速率比干燥空气中高200倍。HASCHKE等[4]对此现象进行了氧化动力学研究，结果表明：空气中的H2O和钚表面发生相互作用，生成的钚氢化物PuHx对钚在空气中的进一步腐蚀有催化作用，造成腐蚀速率大幅增加，同时，催化反应也会消耗氧气和氮气。

钚具有高毒性和高放射性，实验研究面临巨大的挑战，因此，运用理论模拟的方法计算分析空气中各种气体与钚及钚化合物表面的相互作用，对认识钚的腐蚀机理尤为重要。近年来，国内外的许多学者在这方面做了大量的研究。 WANG等[5]采用密度泛函理论(DFT)研究了CO2在α相钚(α-Pu)的(020)表面上的吸附，结果表明CO2完全解离时吸附强度最高。HUDA等[6]利用第一性原理方法研究了δ相钚(δ-Pu)的(100)和(111)表面O原子吸附问题，发现心位是O原子在2种表面吸附的最佳位置，自旋极化作用对总体吸附性质基本无影响。YU等[7]采用GGA+U方法结合过渡态理论(TST) 对H2和H原子在PuO2(110) 表面的吸附、解离和扩散行为，结果表明：H2在PuO2(110) 表面的吸附较弱，但是解离后的H原子与表面O原子的相互作用强度很大，H2的解离势垒为0.48 eV，H原子在表面的扩散势垒为0.3 eV，钚材料表面的PuO2层对于H原子的扩散具有一定的阻挡作用。

在钚的6种同素异形体中，δ-Pu具有良好延展性，最易加工，应用也最为广泛。有关N2分子在δ-Pu(100)表面的微观吸附行为研究还处于空白，对于O2分子在δ-Pu(100) 表面的微观吸附行为，相关研究[8-9]均未对电荷转移情况和Pu—O成键本质进行分析。而Pu—N相互作用和Pu—O相互作用的研究可为钚材料的抗腐蚀研究提供良好借鉴。因此，本文采用第一性原理方法对分别对N2和O2在δ-Pu(100)表面的吸附行为进行研究和分析比较。通过计算各吸附构型的吸附能判断出这2种气体在δ-Pu(100)表面的最稳定吸附构型，对比研究吸附前后δ-Pu(100)表面、N2和O2分子结构的变化以及吸附后2种分子与该表面的结合能分析吸附强度。通过对最稳定吸附构型进行Bader电荷计算，分析吸附分子与δ-Pu(100)表面的电荷转移情况。通过对最稳定吸附构型进行差分电荷密度分析，揭示吸附分子和钚表面原子之间的键演化行为。通过对电子态密度(DOS)计算，分析吸附分子与δ-Pu(100)表面原子间的相互作用本质。

1 计算模型和方法

1.1 计算方法

所有优化计算均利用密度泛函理论框架下的VASP程序[10]完成。在计算中，使用投影缀加波PAW方法[11]展开平面波基组，交换关联效应则使用以PBE泛函表示的广义梯度近似(GGA)方法[12]进行描述，即N、O和Pu元素都采用GGA-PBE赝势处理。在此方法下，Pu元素有16个价电子(6s27s26p66d25f4)，O元素有6个价电子(2s22p4)，N元素有5个价电子(2s22p3)。采用Monkhorst-Pack方法[12]生成布里渊区积分的k点网格，对吸附构型进行优化计算时，格点密度一律设置为5×5×1。在优化过程中，平面波截断能设置为500 eV，电子自洽计算收敛精度设为1×10-5eV，当吸附构型的残余应力小于1×10-4eV/nm时，认为优化完成。

吸附能为负且数值越小，吸附越稳定。吸附分子在δ-Pu(100)表面的结合能为负且数值越小，二者相互作用强度越大，结合越牢固；结合能为正则说明吸附构型不能稳定存在。

吸附能Ea和结合能Eb公式：

Ea=Et-Em1-Es1，

(1)

Eb=Et-Em2-Es2，

(2)

其中，Ea为吸附能，Eb为结合能，Et为优化后吸附构型的能量，Em1为吸附前对吸附分子单独优化的能量，Em2为吸附后从吸附构型中取出的吸附分子能量，Es1为吸附前对δ-Pu(100)表面单独优化的能量，Es2为吸附后从吸附构型中取出的δ-Pu(100)表面能量。

1.2 计算模型

δ-Pu晶体为面心立方结构，优化后计算的晶格常数为a=b=c=0.477 6 nm，α=β=γ=90°，与实验值[6]误差很小，单胞优化结果如图1A所示。对优化好的单胞进行切面，切面采取p(2×2)的4层超晶胞平板模型来模拟δ-Pu(100)表面。为了更充分地模拟表面结构，固定下面2层Pu原子，只让上面2层Pu原子进行驰豫，并且添加了1.5 nm的真空层，优化的表面模型如图1B所示，层间距从上到下依次为0.211 1、0.199 8、0.238 8 nm。

图1 δ-Pu单胞结构及δ-Pu(100)表面模型

在构建吸附模型时，将N2和O2分别置于优化的δ-Pu(100)表面，覆盖度均为0.25，N2中N—N的键长为0.111 3 nm，O2中O—O的键长为0.123 5 nm。N2和O2的初始吸附距离均设为0.2 nm。吸附分子分别置于δ-Pu(100)表面模型的桥位、心位和顶位。由于N2和O2都是直线型分子，吸附分子在每个吸附位置分别考虑3种吸附方向：(1)吸附分子平行于δ-Pu(100)表面且与晶轴平行；(2)吸附分子平行于δ-Pu(100)表面且与晶轴对角线平行；(3)吸附分子垂直于δ-Pu(100)表面。N2和O2在δ-Pu(100)表面的初始吸附构型均有9种(图2)。例如：nb1表示将N2放置于δ-Pu(100)表面的桥位上，N2平行于δ-Pu(100)表面且与表面模型的晶轴方向平行；ot3则表示将O2分子放置于δ-Pu(100)表面的顶位上且O2分子垂直于δ-Pu(100)表面。

n：N2分子吸附；o：O2分子吸附；b：桥位；h：心位；t：顶位；1：吸附分子平行于表面且与晶轴方向平行；2：吸附分子平行于表面且与晶轴对角线方向平行；3：吸附分子垂直于表面。每种构型的左图为俯视图，右图为立体图。

2 结果与讨论

2.1 吸附构型与吸附能

分别对N2和O2在δ-Pu(100)表面的9种吸附构型进行优化，并依据吸附能判断能否发生稳定吸附。结果表明：N2分子在δ-Pu(100)表面的稳定吸附构型有2种，O2分子在δ-Pu(100)表面的稳定吸附构型有6种。优化后的稳定吸附构型如图3所示，H-S-N6表示吸附后N2整体位于δ-Pu(100)表面的心位，2个N原子的连线倾斜于δ-Pu(100)表面且两者与δ-Pu(100)表面Pu原子的成键总数为6；T-P-O2则表示吸附后O2整体位于δ-Pu(100)表面的顶位，2个O原子的连线平行于δ-Pu(100)表面且2个O原子与δ-Pu(100)表面Pu原子的成键总数为2。

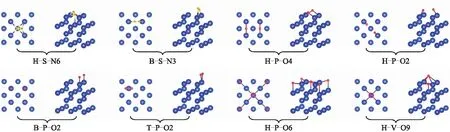
B：桥位；H：心位；T：顶位；P：吸附分子连线与钚表面平行；S：吸附分子连线倾斜于钚表面；V：吸附分子连线与钚表面垂直；Nn/On：2个N原子或O原子与钚表面原子成键的总数为n。每种构型的左图为俯视图，右图为立体图。

结合图3对表1的参数值进行分析可知，N2仅在δ-Pu(100)表面的心位和桥位发生稳定吸附，桥位不能发生吸附。吸附后N2倾斜于δ-Pu(100) 表面，N—N键变长，心位吸附键长增加了0.029 4 nm，桥位吸附键长增加了0.009 6 nm。N2吸附后没有发生解离，2个N原子在心位的吸附高度明显小于在桥位的吸附高度。对比2种构型的吸附能可得，心位吸附比桥位吸附放出的热量多，二者相差0.558 0 eV。从结合能上看，心位吸附中N2与δ-Pu(100) 表面的结合强度也远大于桥位吸附。以上结果表明，N2在δ-Pu(100) 表面心位吸附的稳定性比在桥位吸附的大，最稳定吸附构型为H-S-N6。另外，根据二者吸附能和吸附后N—N键长的增加程度可以初步推测，N2与δ-Pu(100) 表面心位为化学吸附，在桥位则为物理吸附。

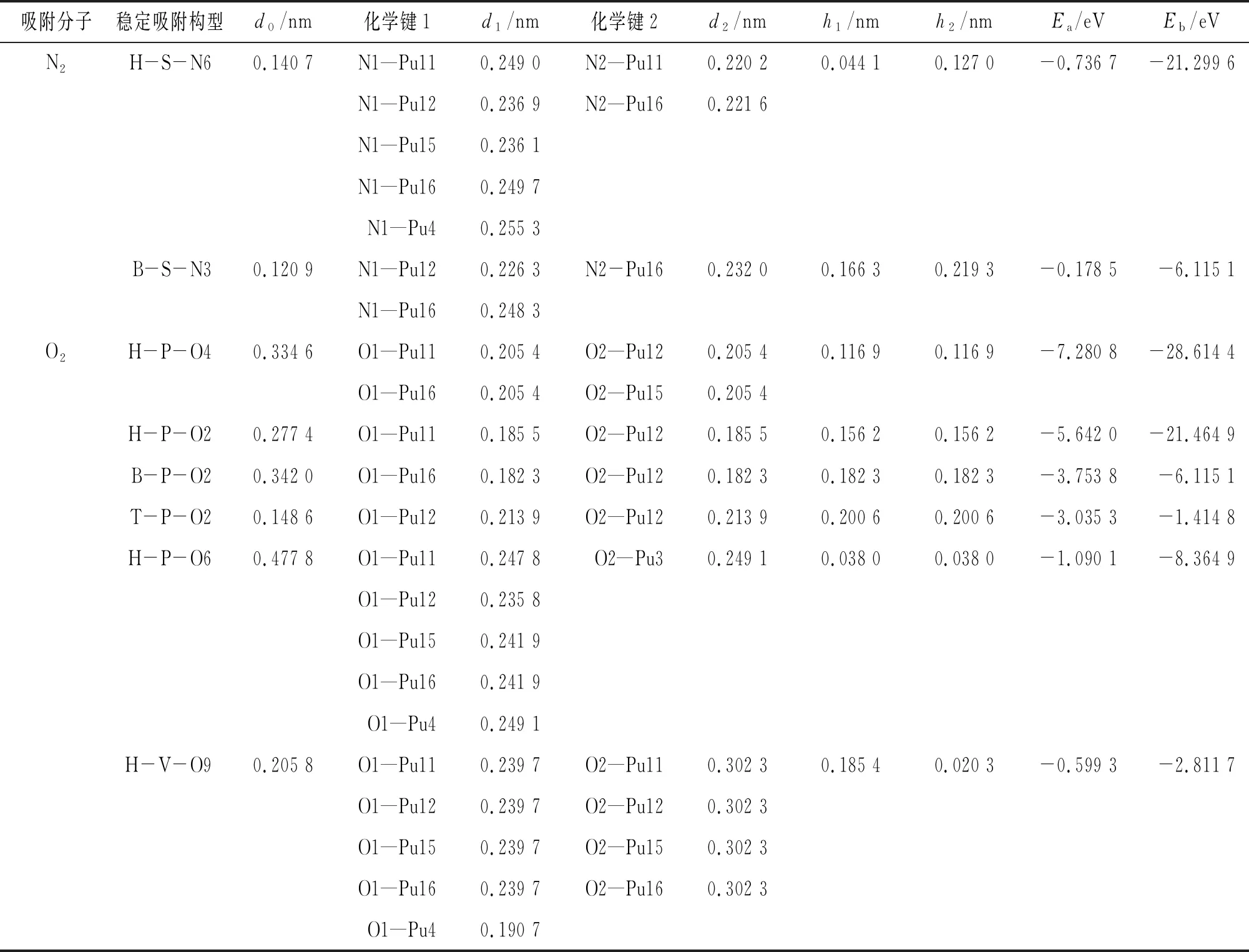
表1 N2和O2在δ-Pu (100) 表面稳定吸附构型的结构参数和能量数据

O2在δ-Pu(100) 表面的吸附强度远比N2的大。O2在心位、桥位和顶位都可以稳定吸附，在心位和桥位吸附后，O2解离为2个O原子，在顶位吸附后，O2键长增加了0.025 1 nm，未发生解离。与N2分子的吸附情况不同，O2分子吸附后，2个O原子的连线分为与δ-Pu(100) 表面垂直和平行这2种情况，而且，平行时的吸附能普遍大于垂直时的吸附能。O原子与第1层Pu原子的距离在0.020 3～0.200 6 nm范围，且与吸附位置及吸附能无关。对比分析各种吸附构型的吸附能和结合能可得，H-P-O4构型放出的热量最多，是最稳定的吸附构型，O原子与δ-Pu(100) 表面的结合强度也最大。这表明O2在δ-Pu(100) 表面的吸附为强化学吸附，吸附稳定性和结合强度的大小顺序均为心位、桥位、顶位。

为进一步比较N2和O2在δ-Pu (100) 表面吸附的异同，对2种分子各自的最稳定吸附构型进行分析。吸附构型H-S-N6是由图2中初始构型nb2优化而来的，从初态到末态，N2发生翻转，N1原子逐渐向心位移动，N2原子逐渐向桥位移动，N2吸附后未发生解离，仍以分子态吸附于δ-Pu(100)表面，仅N1—N2键被活化，键长增加了0.029 4 nm。根据过渡态理论，利用VTST程序中的CI-NEB方法[16]计算可得，此吸附过程的发生需越过0.54 eV的能垒。吸附构型H-P-O4是由图2中的初始构型oh1优化而来的，从初态到末态，O2的2个O原子逐渐分离并向两侧移动，最终O1原子处于Pu11和Pu16原子的桥位，O2原子处于Pu12和Pu15原子的桥位。与N2吸附不同的是，在O2的最稳定吸附构型中，O2发生解离吸附。而且，利用相同方法[16]计算可得，O2的解离不需要越过势垒，这也说明了O2分子吸附为强化学吸附。如图4所示，N2分子吸附后，表面功函增加了0.591 eV；O2分子吸附后，表面功函增加了1.141 eV。这说明2种分子的吸附都会使δ-Pu(100) 表面功函增加，电子从表面逸出的难度增大，这是因为N2和O2分子的存在使δ-Pu(100) 表面的偶极矩发生变化，表面Pu原子失电子，N原子或O原子得电子，由此在表面形成了电偶极层。由于O原子的电负性要强于N原子，Pu原子与O原子相互作用强度要强于N原子，表面功函增加较多。

图4 吸附前后体系的静电势随Z轴方向距离的变化

对于O2分子在δ-Pu(100)表面的吸附而言，本文对吸附构型和吸附能的计算结果与文献[10]、[11]的计算结果有一些差异。本文所得的最稳定吸附构型H-P-O4是从初始构型oh1优化而来，即初始放置于心位且与δ-Pu(100)表面平行的O2分子优化后发生了解离，解离出的2个O原子对称吸附于两侧的桥位，其吸附能为-7.281 eV。郭继军等[10]的计算结果显示，初始放置于桥位的O2分子吸附后发生了解离，解离出的2个O原子分别稳定吸附于δ-Pu(100) 表面的2个心位，此时吸附最稳定，吸附能为-7.290 eV。HUDA的计算结果[11]表明，初始放置于心位且与δ-Pu(100) 表面平行的O2分子吸附后同样发生了解离，解离出的2个O原子分别稳定吸附于δ-Pu(100)表面的2个心位，吸附能为8.236 eV。 对于表面功函的计算，本文和相关文献[6,10,11]的计算结果都表明O原子或O2分子的吸附会使δ-Pu(100) 表面的表面功函增加。本文的计算出的最稳定构型的表面功函增量是最大的，即1.141 eV，之前学者计算出的结果均小于1 eV，其差异可能因计算程序和方法的不同以及所建立的模型引起的。如本文研究利用VASP程序完成，采用PBE泛函描述交换关联效应，而相关文献[6,11]均利用DMOL3程序进行计算，交换关联效应则采用PW或PW91泛函来描述。本文采用4层slab模型，其余文献[6,10,11]均采用3层slab模型，产生模型上的差异在所难免。

2.2 N2和O2吸附的Bader电荷分布对比

原子或分子在金属或金属氧化物体系表面的吸附和扩散必然伴随着电荷的转移[17-19]。利用Bader电荷计算方法[20]可以对吸附分子与δ-Pu(100) 表面的电荷转移情况进行分析。表2中的数据为吸附前N2分子、O2分子、δ-Pu(100)表面以及吸附后各稳定吸附构型的净电荷值。分析表2中的数据可知，吸附后，2个N原子和2个O原子均得到电荷，且各吸附构型中N或O所得到的电荷总和与4层δ-Pu(100)表面Pu原子所失电荷的总和相等，这意味着δ-Pu(100)表面Pu原子向吸附原子发生了电荷转移。在N2分子的2种稳定吸附构型中，心位吸附比桥位吸附的电荷转移量大，在O2分子的6种稳定吸附构型中，电荷转移量从大到小的顺序：心位、桥位、顶位。对比N2分子和O2分子的吸附构型可知，无论是在心位还是桥位，O2分子吸附构型中的电荷转移量都大于N2分子吸附构型中的电荷转移量。分析表2中的数据可知，电荷转移量越大，吸附构型越稳定，则吸附过程放热越多，相应吸附强度也越大。

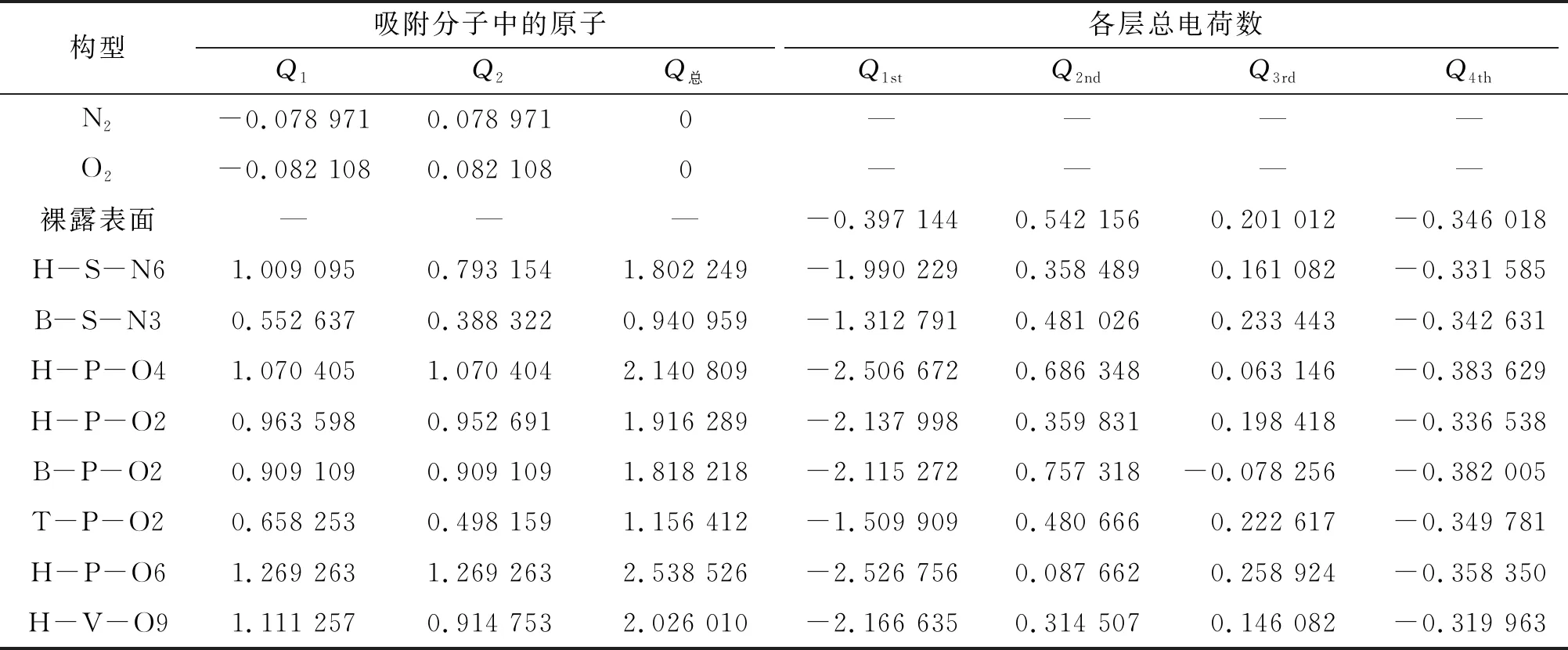
表2 各稳定吸附构型的净电荷分布

在所有稳定吸附构型中，δ-Pu(100)表面Pu原子的电荷变化量最大，普遍表现为失电子(-2.129 612 e～-0.915 647 e)；次表层Pu原子电荷变化量远小于表层，有的构型得电子，而有的构型失电子，得失电子范围-0.454 494 e～0.215 162 e；第3层Pu电荷变化量小于次表层，得失电子范围-0.279 268 e～0.057 912 e；底层Pu原子总电荷变化量可忽略不计。这些现象说明N2分子或O2分子在δ-Pu(100)表面吸附过程中，主要是与上面3层Pu原子发生相互作用，且从上至下相互作用程度依次递减。有研究[6,10-11]利用3层δ-Pu(100)表面模型同样表明O原子与最外层Pu原子间的电荷转移程度最大。这再次说明4层δ-Pu(100)表面模型对于研究活性分子吸附已足够[21-22]。图5显示了吸附前纯净δ-Pu(100)表面以及吸附后2种气体的最稳定吸附构型中原子所带电荷的情况，从图中可以很明显地看出在吸附前后δ-Pu(100)表面电荷变化情况，与表2中的数据一致，吸附分子的原子与第一层Pu原子相互作用最强。

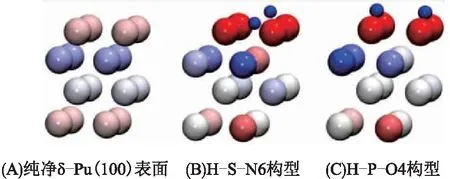
图5 吸附前纯净δ-Pu(100)表面以及吸附2种气体后最稳定吸附构型中原子的电荷着色图

2.3 N2和O2吸附表面的电子结构分析

2.3.1 差分电荷密度分析 差分电荷密度图可以更加直观地显示吸附构型中电荷分布情况，对分析吸附原子与δ-Pu(100)表面Pu原子之间电荷转移和成键情况有重要的作用[23-24]。

差分电荷密度:

Δρ=ρA+B-ρA-ρB,

(3)

其中，Δρ为差分电荷密度值，ρA+B为吸附构型的电荷密度值，ρA为吸附后吸附分子的电荷密度值，ρB为吸附后δ-Pu(100)表面的电荷密度。

N2的最稳定吸附构型H-S-N6(图6A)中，N1和N2原子主要与表层的Pu11、Pu12、Pu15、Pu15和Pu16原子相互作用，而且，对比分析N1原子与这4个Pu原子的成键电荷密度可得，N1原子在靠近Pu原子的一侧，电荷密度增加，另一侧则电荷密度减少；Pu原子则正好相反，靠近N1原子的一侧电荷密度减少，另一侧电荷密度增加。N2原子与Pu11和Pu16原子成键的电荷密度分布与也具有相似的特征。总体而言，在2个N原子各自的局部区域，电荷密度增加的程度远大于电荷密度减少的程度，说明在N原子附近出现了高浓度的电荷分布。然而，在表层Pu原子各自的局部区域，电荷密度增加的程度都小于电荷密度减少的程度，说明表层Pu原子出现了电荷损耗。这些现象意味着电荷从表层Pu原子向2个N原子转移，也表明吸附后Pu—N键具有离子性。而且，由于N2分子的2个N原子与表层Pu原子的相互作用，N—N键区域的电荷密度严重减少，键的强度被削弱，电子向两侧的N原子转移。

图6 H-S-N6和H-P-O4的差分电荷密度

在O2的最稳定吸附构型H-P-O4(图6B)中，O1和O2的位置具有高度对称性，O1—Pu11、O1—Pu16、O2—Pu12和O2—Pu15键几乎完全相同。以O1—Pu16键为例分析可知，O原子附近电荷密度增加的程度远大于电荷密度减少的程度，发生了明显的电荷累积现象。与此相反，Pu原子附近的电荷密度增加的程度小于电荷密度减少的程度，且靠近O原子的一侧电荷密度明显减少。这意味着Pu原子的电荷向O原子发生了转移，Pu—O键具有明显的离子性。而且，2个O原子之间区域的电荷密度均减少，O—O键完全断裂。值得注意的是，在次表层Pu原子各自的局部区域，都出现了电荷密度增加的现象，说明δ-Pu(100)表面催化了O2分子的解离，O—O键断裂和Pu—O键形成的过程也导致了δ-Pu(100)表面层间电荷密度的重排。

对比分析图6A和图6B不难发现，δ-Pu(100)表面与O原子之间的电荷转移程度比与N原子之间的电荷转移程度大，O2分子的吸附对δ-Pu(100)表面的电子排布造成的影响也远远强于N2分子的吸附。相同的是，Pu—N相互作用和Pu—O相互作用都具有离子性，Pu—O键的离子性更加明显。原因可能是O原子的电负性比N原子的强，O2分子更易被活化。

2.3.2 电子态密度分析 通过对体系的总态密度(TDOS)和分波态密度(PDOS)进行分析，可以更加具体地了解吸附体系的电子结构以及吸附分子或原子与被吸附表面的相互作用本质[24-25]。从图7可以看出，纯净δ-Pu(100)表面的电子局域化程度很高，电子态主要集中于-47～-44 eV、-21～-17 eV和-5～0.5 eV这3个能量区间内，并且高能区域的态密度峰值和电子态数目比低能区域的大。-47～-44 eV区间的态密度主要由Pu 7s轨道贡献，-21～-17 eV区间的态密度主要由Pu 6p轨道贡献，-5～0.5 eV区间的态密度主要由Pu 6d和Pu 5f轨道贡献。N2吸附后，最稳定吸附构型(H-S-N6)与纯净δ-Pu(100)表面相比，电子局域特性基本不变，Pu 7s轨道峰值和展宽幅度均减小，Pu 6d轨道峰值略有减小，展宽基本不变，Pu 6p和Pu 5f轨道峰值和展宽均有大幅度增加。O2吸附后，最稳定吸附构型(H-P-O4)与纯净δ-Pu(100)表面相比，电子局域特性也基本不变，Pu 7s轨道能量较低峰的峰值减小，能量较高峰的峰值增大，总的电子态数目不变，Pu 6p、Pu 6d和Pu 5f轨道都出现了峰值减小而展宽增大的现象，说明Pu 6p、Pu 6d和Pu 5f轨道电子局域化程度降低，能级发生弥散和劈裂。吸附后，N原子和O原子的轨道对体系总态密度的贡献很小.

图7 δ-Pu(100)表面吸附N2和O2前后最稳定构型的态密度

单独分析吸附前后N2和O2的总态密度(图8)可知，N2吸附前，最高占据轨道 (HOMO) 为5σ成键轨道，最低空轨道 (LUMO)为2π*反键轨道；N2吸附后，5σ轨道相对于费米能级的能量基本不变，1π轨道相对于费米能级能量上升，并且与5σ轨道重叠，2π*轨道相对于费米能级能量下降，空轨道部分展宽增大，电子态数目增多。O2吸附前，最高占据轨道 (HOMO) 为2π*反键轨道，最低空轨道 (LUMO) 为6σ轨道；O2解离吸附后，O2所有占据轨道断裂，空轨道部分明显拓宽，电子态数目增多。

图8 最稳定吸附构型在吸附前后N2和O2的总态密度图

N2在吸附过程(图7、图8)中，主要是1π、5σ及2π*轨道与Pu 7s、Pu 6p、Pu 6d和Pu 5f轨道发生重叠杂化作用，导致吸附体系总能量下降，与Pu 6p和Pu 5f轨道的相互作用较强，与Pu 6d轨道的相互作用最弱。 O2在吸附过程中，所有占据轨道都与Pu 7s、Pu 6p、Pu 6d和Pu 5f轨道发生强烈的重叠杂化作用，导致所有的占据轨道消失，与Pu 6p和Pu 5f轨道的相互作用较强，与Pu 7s和Pu 6d轨道的相互作用较弱。

为了更加直观地比较吸附后2种最稳定吸附构型中Pu—N键和Pu—O键的相互作用强度，利用LOBSTER程序[26]对键长由大到小的Pu—N相互作用以及Pu—O相互作用的COHP和ICOHP[27]进行了计算，COHP为正代表成键作用而为负代表反键作用。在费米能级以下，H-S-N6构型中(图9)，3种距离Pu—N相互作用基本为正值，说明在费米能级之下Pu原子与N原子为成键相互作用。ICOHP为费米能级之下COHP的积分，直接反映了2个原子间的相互作用强度。Pu11—N2、Pu11—N1和Pu4—N1的ICOHP分别为2.797 03、1.078 03和0.996 06，表明相互作用强度由大到小的顺序为Pu11—N2、Pu11—N1、Pu4—N1。根据表1，相互作用距离由小到大的顺序为Pu11—N2、Pu11—N1、Pu4—N1，说明相互作用距离越小则成键强度越大。 在H-P-O4构型中，Pu11—O1、Pu16—O1、Pu12—O2和Pu15—O2的相互作用距离和对称性变化基本一致，所以仅以Pu11—O1为例进行计算。同样，在费米能级以下(图9中虚线位置)，Pu—O相互作用有明显的成键态出现，ICOHP为3.975 80，说明其成键强度明显大于Pu—N相互作用。从图10可看出，在H-S-N6中，N 2s轨道与Pu 6p和Pu 6d轨道有微弱的重叠杂化作用，N 2p轨道和Pu 6p、Pu 6d和Pu 5f轨道的重叠杂化作用较强；在H-P-O4中，O 2s轨道与Pu 6p和Pu 6d轨道有微弱的重叠杂化作用，O 2p轨道与Pu 6d和Pu 5f轨道有较强的重叠杂化作用。总之，Pu—N相互作用的本质为N 2s和N 2p轨道与Pu 6p、Pu 6d和Pu 5f轨道的重叠杂化作用，同样，Pu—O键形成的本质也为O 2s和O 2p轨道与Pu 6p、Pu 6d和Pu 5f轨道的重叠杂化作用。

图9 2种最稳定吸附构型 (H-S-N6、H-P-O4) 中不同化学键的COHP

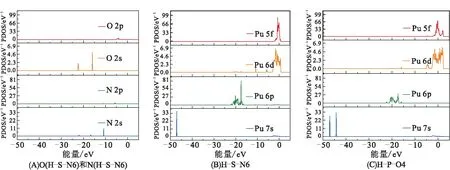
图10 2种最稳定吸附构型的分波态密度

3 结论

采用第一性原理方法分别对N2分子和O2分子在δ-Pu(100)表面的吸附行为进行了理论研究。结果表明：N2分子在δ-Pu(100)表面吸附为分子吸附，吸附稳定性和吸附强度从大到小均为心位、桥位，最稳定吸附构型为心位倾斜构型(H-S-N6)；O2分子在δ-Pu(100)表面的桥位和心位均为解离吸附，在顶位则为分子吸附。总体而言，吸附稳定性和吸附强度从大到小均为心位、桥位、顶位，最稳定吸附构型为心位平行构型(H-P-O4)。

首先，N2分子和O2分子在δ-Pu(100)表面吸附后都会使表面功函数增大，电子从表面逸出难度增大，其中，O2分子的吸附使表面功函数的增大程度要大于N2分子的吸附；其次，Bader电荷分析的结果表明N2分子和O2分子吸附后均得到电子，δ-Pu(100)表面失去电子，且N原子和O原子主要和表面3层Pu原子发生电荷转移作用，和底层Pu原子基本不发生电荷转移，且O原子与表面Pu原子之间的电荷转移量高于N原子；第三，吸附后N2分子化学键被活化，键长增大了0.029 4 nm，主要原因是1π、5σ及2π*轨道与Pu 7s、Pu 6p、Pu 6d和Pu 5f轨道发生重叠杂化作用；O2吸附后化学键断裂，其原因也是Pu 7s、Pu 6p、Pu 6d和Pu 5f轨道与O2分子轨道的相互作用；第四，结合分析COHP的计算结果和2种最稳定吸附构型的分态密度计算结果可得，吸附后，N原子与表面近邻Pu原子形成化学键，其原因主要是N 2s和N 2p轨道与Pu 6p、Pu 6d和Pu 5f轨道的重叠杂化作用，同样可得，吸附后，O原子与表面近邻Pu原子也形成了化学键，而且，Pu—O键的键能大于Pu—N键，主要原因是O 2s和O 2p轨道与Pu 6p、Pu 6d和Pu 5f轨道的重叠杂化作用。

N2和O2在δ-Pu(100)表面的吸附均为化学吸附，O2的吸附远强于N2的吸附。研究结果为理解N2和O2在δ-Pu(100)表面的共吸附行为提供了理论指导。