基于随机森林的沪深300预测研究

文/李岩（中国人民大学）

一、引言与文献综述

预测金融指数的趋势是非常复杂且困难的，它包含了太多不确定因素，影响单只股票市场价值的因素更具体，如公司的财务报表、发行可转债、对外订立合约、突发的政治经济舆论事件、大规模资金的买入卖出、投资者对一个特定的公司的情绪等，这就造成了单只股票波动的可预测性比较低。相比来说，股指作为一揽子股票，比单只股票更具有可预测性和难以被控盘性，更容易使用技术进行预测。当然，金融市场的本身影响因子复杂，波动性高，这决定了股指趋势预测的困难性和必要性，准确预测有利于降低风险，也可以更好地掌握经济发展势头，为国家的整体发展投资贡献力量。预测股指价格的方法总结有：（1）技术分析（Technical Analysis)，使用技术指标进行分析趋势；（2）时间序列预测（Time Series Forecasting )，将价格作为时间序列进行分析；（3）微分方程（Differential Equation），使用微分方程对股指波动进行建模和预测；（4）机器学习（Machine Learning)和数据挖掘（Data Mining)。

本文主要研究的是第四种方法，利用股票市场的大数据集，使用随机森林的分类方法进行处理。机器学习模型在股票市场行为中是一个新的应用。该方法与传统的预测方法有所不同。早期使用技术指标进行股票价格预测，夏毅和蓝伯雄（2004）[1]证明了中国股票市场弱有效状态下的技术分析的有效性问题。赵国顺（2009）[2]基于时间序列分析技术分析股票价格趋势；王晓晔和王正欧（2004）[3]又对时间序列方法进行了改进，通过正则化训练的神经网络与粗集理论相结合的股票时间序列数据挖掘技术，预测效果比单纯时间序列要好。在微分方程的应用方面，李凯（2014）[4]应用了随机微分方程为股票期权定价。在机器学习的应用方面，也有国内外不少学者进行了探索，Li等(2014)[5]利用logistic回归模型并考虑了股票价格对外部条件的敏感性，预测成功率为55.65%。Devi等（2015)[6]利用混合的支持向量机模型，采用了RSI、货币流量指数、均线、随机振荡器和MACD等技术指标，进行了预测。总体来看，股票价格具有的混沌性和高波动性，使预测其确切的价值变得非常困难，因此将股票预测作为分类问题处理，比将其作为回归问题处理，不需要那么精确的预测结果，相对会取得更好的效果。在本次研究中，使用一种集成学习算法，即随机森林对股票指数进行预测。

二、理论介绍

（一）基本假设－有效市场假说

使用预测算法来确定股票市场价格的未来趋势通常建立在有效市场假设前提下，也就是当前的股票价格完全反映了所有相关信息。它意味着，如果有人想通过分析历史股票数据获得优势，那么整个市场就会意识到这个优势，结果，股票的价格就会被修正。这是一个极具争议的理论，当然此假设不是本次研究的重点，我们暂时接受这一假设并在这一假设基础上做研究。

（二）随机森林

随机森林是将一组决策树模型进行袋装，通过对多个决策树产生结果投票，根据少数服从多数的原则，对产生最终的分类决策。该方法减少了构建决策树时常见的方差和过拟合问题，提高了学习算法的稳定性和准确性，单一的决策树具有非常低的偏差和高方差，可能会导致：为了学习精度而把树长得非常深，这种情况往往会过度训练集；数据中的轻微噪音也可能会导致树以完全不同的方式生长，随机森林通过在特征空间的不同子空间上训练多个决策树以略微增加偏差为代价克服了这个问题。这意味着森林中所有的树都看不到整个训练数据。数据被递归地分割成多个分区。随机森林有众多优点，如：对特征很多的数据也可以适用, 不用降维，不需要做特征选择；可以输出特征的重要性排序，方便逻辑解释；可以判断出不同特征之间的相互影响；训练速度比较快；不容易过拟合；可以适用不平衡的数据等。

（三）决策树

随机森林的基础是决策树，那么决策树的节点是怎么排序的呢，原则是信息增益最大的排前面，由分裂引起的信息增益可计算如下：

其中I(N)是节点N的Gini impurity或香农熵，PL是节点N在划分后去往左边子节点的比例，PR是节点N在划分后去往右边子节点的比例，NL和NR分别是左右节点。

Gini impurity作为衡量每个节点划分质量的函数，公式为：

其中P(Wi)是类别标签i的总体比例。

香农熵也可以用来判断分裂质量，它衡量信息内容的混乱程度，是信息量的数学期望。在决策树中，香农熵用于衡量树的特定节点中包含的信息的不可预测性，节点N的熵计算公式为：

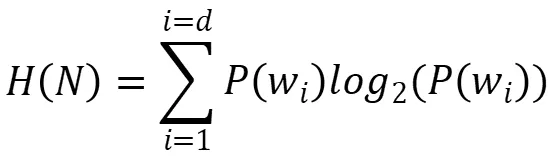
其中d是类别的数量，P(Wi)是第i个类别标签占总体的比例。

三、模型建立

技术指标，是利用时间序列价格计算的参数，旨在预测价格方向。它们是投资者广泛用于预测市场看跌或看涨信号的工具。我们将价量数据Open开盘价、High最高价、Low最低价、Close收盘价、Volume交易量及技术指标数据MA5、MA10、MA20、MA60、MACD_DIF、MACD_DEA、 MACD_MACD、KDJ_K、KDJ_D、KDJ_J、CCI_CCI、DMI_PDI、DMI_MDI、DMI_ADX、DMI_ADXR、 DMA_DIF、TRIX、CR、VR、OBV、ASI进行收集，研究数据均来自公开的交易数据，收集了2010年1月1日至2021年12月31日的399300指数数据进行测试，这些数据构成了我们的整个数据集。接下来将数据进一步分为训练集(整个数据的90%)和测试集(整个数据的10%)。并且将数据轮流做测试集10次，以提高模型的准确度，将模型进行拟合训练。

研究使用的随机森林算法创新性地采用一日一训练的方法进行预测，即按照今日的实际涨跌数据，投入下一轮训练，得出次交易日的预测数据，以此类推，相当于每日训练一次模型，改变过往只预测一次的方法，阈值选用0.5，即在预测概率大于0.5时，预测股票指数的次日将上涨，即预测次日的收盘价将大于开盘价，操作是在次交易日的开盘价买入，收盘价卖出，来计算实际收益。举个例子，使用截止到今日的实际数据，预测股票指数的次日的涨跌情况，使用次日的实际价格重新投入训练，预测后日的涨跌情况，以此循环往复，计算所有日期的预测综合效果。

四、模型效果

在模型的效果评价方面，采用了AUC和净值法。

AUC（Area Under Curve）被定义为ROC曲线（Receiver Operating Characteristic）与下坐标轴之间的面积，ROC曲线接近ROC的左边沿和上边沿时，也就是曲线下的面积越大，测试越准确。如果曲线接近ROC空间的45度对角线，则意味着测试不准确。当然也要考虑金融预测的复杂性，AUC的界值不需要设的很高，实际操作中，可以很容易地通过sklearn 包中的metrics.roc_auc_score函数来计算出随机森林模型预测的准确率是0.52。

利用我们的模型产生的预测结果，可以判断次日的涨跌，进而进行买卖决策。如果预测是1，这意味着次日的指数收盘价会高于开盘价，那么交易建议是购买指数。而如果预测是0，表示价格预期是下跌，收盘价会低于开盘价，建议按兵不动。最终形成的净值曲线如图1所示。可以计算得出11年的净值为1.929395，相比沪深300指数净值1.392133有明显提升，从图1中也可以看出对曲线的波动率有明显的平滑作用。

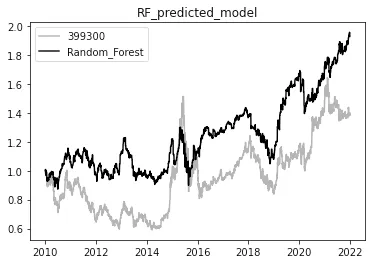
图1 随机森林与399300指数对比净值图

五、结论与建议

由于股票市场的非线性、动态性和复杂性，对其进行预测是非常困难的。然而，近年来，机器学习技术在股票预测中被证明是有效的。研究使用了随机森林分类器和众多的技术指标因子来建立我们的预测模型，通过计算准确性和净值等参数来评估模型，产生了1.9的净值效果并有效平滑了波动，预测准确率为52%，考虑到股票市场的复杂性和不可完全预测性，模型被证明可以预测未来的股票指数运动方向。随机森林分类的预测股指的意义在于，非线性的问题也可以用线性判别型机器学习算法来解决，生活中，尤其是金融领域，很多问题都不是线性可分的，在这类问题中，所采用的解决方案方法需要一种范式转换，做出微小修改可能会使思路更加宽广。

随机森林模型对股值预测是技术上的扩展，也是对技术指标的创新应用，是传统与新时代的碰撞。模型可以用来设计新的交易策略、应用在新的品种上执行股票投资组合管理，预测股指趋势来选取一揽子股票进行投资。未来的发展改进主要有四个方面：

（1）模型时间上的扩展应用，在未来的工作中，可以建立随机森林模型来预测以小时或分钟为单位的短时间窗口的趋势，更好地为市场提供流动性，也可以预测周或月为单位的趋势，较长周期的预测可以更好地掌握经济发展势头，为国家的整体发展投资贡献力量；

（2）模型阈值的更改，现在选取0.5作为决策阈值，可以根据风险承受能力，选取在不同阈值下的收益与风险的平衡值；

（3）不同机器学习算法的集合也可以检查其在股指预测的鲁棒性。

相关链接

随机森林指的是利用多棵树对样本进行训练并预测的一种分类器。该分类器最早由Leo Breiman和AdeIe CutIer提出，并被注册成了商标。

在机器学习中，随机森林是一个包含多个决策树的分类器， 并且其输出的类别是由个别树输出的类别的众数而定。 Leo Breiman和AdeIe CutIer发展出推论出随机森林的算法。